Regularization 은 L1 과 L2 로 나눌 수 있으므로 이번 글에서는 먼저 L1 에 대해 알아보자.
Contents
- L1 regularization
- Hyperparameter: alpha
- Graphical analysis
- Useless features in Lasso
1. L1 regularization
An L1-regularized linear regression adds |coef| as the penalty term.
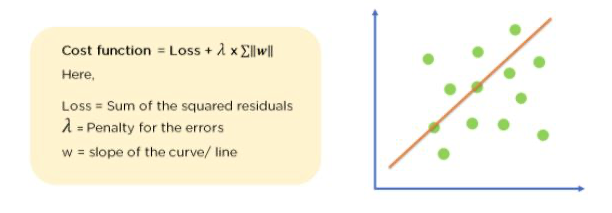
L1 regularization 은 가중치의 절댓값을 벌칙으로 부과한다. 특히 이를 선형 회귀에 적용시킨 경우 "Lasso" 라는 명칭을 얻게 된다. Sci-kit learn 에서 제공하는 Lasso() class 를 통해 55개의 특성을 가지며 표준화 처리가 완료된 훈련 데이터를 다시 학습시켜보자.
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target)) # 0.989389309375173
print(lasso.score(test_scaled, test_target)) # 0.98037049351184952. Hyperparameter: alpha
Sci-kit learn 의 Lasso() 와 Ridge() class 모두 "alpha" 라고 하는 parameter 를 갖는다.
이는 "규제 강도" 를 나타내는데, alpha = 1 (default) 이며 당연하게도 alpha 가 높아질수록 규제는 더욱 세진다. 참고로 alpha 는 음수가 아닌 float 이어야 한다.
Constant that multiplies the L1 term, controlling regularization strength.
우리가 직접 정해야 하는 매개변수들을 "hyperparameters" 라고 정의했었다. 반대로 모델이 직접 학습하는 값들은 "model parameters" 라고 한다. 그렇다면 우리는 적절한 규제 강도를 찾기 위해 alpha 값들을 바꿔가며 실행시켜봐야 하므로 hyperparameter 를 탐색해 볼 것이다. 이를 하나하나씩 넣어보는 것은 효율적이지 않으므로 가장 간단하면서 편리한 방법으로 alpha_list 와 for 문을 사용해보자.
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
lasso = Lasso(alpha=alpha)
lasso.fit(train_poly, train_target)
train_score.append(lasso.score(train_poly, train_target))
test_score.append(lasso.score(test_poly, test_target))
alpha_list 를 보면 숫자들이 10배씩 증가하는 것을 알 수 있다. 이와 같은 상용로그 스케일은 conventionally 사용해오던 것으로, 이후 점점 더 나은 범위를 좁혀 나가는데 유용하다. 또한, 상용로그 스케일을 사용함으로써 결과들을 그래프로 나타내고자 할 때 log10 을 이용해 x축의 간격을 동일하게 해준다.
3. Graphical analysis
앞서 얻은 score 들을 우리는 각각 train 과 test 리스트에 저장해주었다. 따라서 alpha 값들을 log10 으로 변환해 해당 결과들과 함께 그래프를 그려주면 다음과 같은 결과를 얻는다.
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()그래프를 보면 훈련 세트에 대해서는 점수의 변동이 거의 없으며 전체적으로 테스트 세트와의 점수 차이가 크다. 즉, 규제가 제대로 이루어지지 않았음을 알 수 있다.
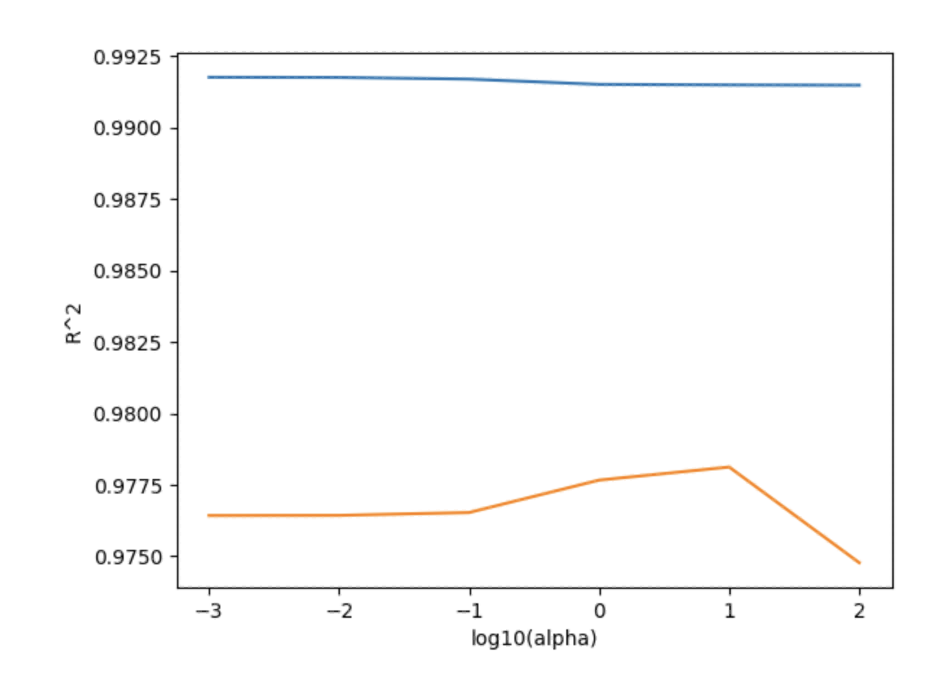
그럼에도 불구하고 alpha = 10 인 지점에서의 점수차가 제일 작으며 test set 의 점수 또한 나쁘지 않으므로 이 지점을 골라 모델을 다시 훈련시켜보자. Lasso() class 안에 alpha 를 새로 지정해주면 된다.
lasso = Lasso(alpha=10)
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target)) # 0.988550904736282
print(lasso.score(test_scaled, test_target)) # 0.9826075271887963결과적으로 음수로 떨어졌던 테스트 세트의 점수가 훨씬 개선되었음이 보인다. 하지만 일반적으로 L2 규제가 L1 보다 조금 더 효과적이므로 다음에는 L2 regularization 에 대해 알아보도록 하겠다.
4. Useless features in Lasso
Lasso regression 의 특징들 중에는 또한 일부 특성을 아예 사용하지 않을 수도 있다는 것이다. Regression 모델에서 각각의 특성은 가중치가 곱해지므로, 사용하지 않는 특성들은 가중치가 0 인 경우에 해당한다.
print(np.sum(lasso.coef_ == 0)) # 48이를 통해 우리는 총 55개의 특성들 중 48개를 제외한 오직 7개의 특성이 Lasso regression 에 사용되었음을 알 수 있다. 이렇듯 일부 특성을 사용하지 않는 것이 좋지 않다고 얘기하긴 어렵지만 일반적으로 규제 모델을 이용할 때는 위에서 언급한 등의 이유로 L2, 즉 Ridge 규제가 더 선호된다.