AI/ML/DL (15) - Multiclass classification

Contents

1. Multiclass classification
2. One-versus-Rest (OvR)
3. Softmax

---

1. Multiclass classification

이번 글에서는 총 7개의 채소들에 대한 분류를 수행해보자. 이를 위해 logistic regression 의 parameters 를 알아볼 필요가 있다.

• C: float, default=1.0
  Inverse of regularization strength (smaller values specify stronger regularization).
• max_iter: int, default=100
  Maximum number of iterations taken for the solvers to converge.

𝛼 와는 반대로 C 는 규제 강도에 반비례한다. 따라서 조금 더 복잡한 모델을 만들기 위해서는 C 를 늘려 규제를 약화시켜야 한다. 또한 iteration 의 수를 조절할 수 있는 max_iter 는 반복 횟수가 모자르지 않도록 충분히 설정해주어야 한다.

lr = LogisticRegression(C=20, max_iter=1000)
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled, train_target)) # 0.9327731092436975
print(lr.score(test_scaled, test_target)) # 0.875

위와 같이 규제 강도는 낮추고 학습 횟수는 늘려 기존의 logistic regression model 을 새로 학습시킨 후 score 를 출력한다면, 이는 분류의 정확도를 의미한다. 이를 바탕으로 test set 에 대한 예측을 해보자.

proba = lr.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=3))

각각의 row 는 test_scaled 의 샘플을 나타내고 총 7개의 확률들 중 제일 높은 것이 유력한 채소의 종류가 된다.

---

2. One-versus-Rest (OvR)

로지스틱 회귀의 계수 및 절편의 shape 을 출력해보면 다음과 같다.

print(lr.coef_.shape, lr.intercept_.shape) #(7, 5) (7,)

계수는 총 7개의 row 와 5개의 column 으로 이루어져 있는데, 이는 7개의 classes 와 5개의 특성들을 의미한다. 즉, 각각의 class 에 대한 z값이 존재함을 알 수 있다. 이때, 각 샘플들의 특성값들을 7개의 decision function 에 대입해 얻는 가장 큰 z 에 해당하는 class 가 양성인 것이다. 이와 같은 다중분류를 one-versus-rest (OvR) 라고 한다.

• 그렇다면 총 7개의 z 를 sigmoid 에 통과시킬 시 합이 1이 되어 확률처럼 간주할 수 있는가?
  아니다. 이진분류을 참고하면 decisions 를 expit() 함수에 적용시켰을 때 각각의 샘플 내에서는 합이 1이 되지만 양성 class 에 관한 z값을 다 더하면 1을 넘기게 된다.

따라서 7개의 z 를 sigmoid 에 그대로 넣어서는 안되며, 특히 다중분류에서는 sigmoid 대신 softmax 라는 함수를 사용해야 한다.

---

3. Softmax

Sigmoid 함수와 마찬가지로 Scipy 에서 softmax 함수를 제공한다.

softmax(x) = np.exp(x)/sum(np.exp(x))

Softmax 는 각 행의 z 값을 exponential function 에 적용한 후 sum = $e^{z_0}+e^{z_1}+e^{z_2}+e^{z_3}+...+e^{z_6}$ 으로 각각을 나누어 결국 총합이 1이 되도록 한다. 예를 들어 test_scaled[0] 의 decision function 은 아래와 같다면 각각의 softmax 값은 다음과 같다.

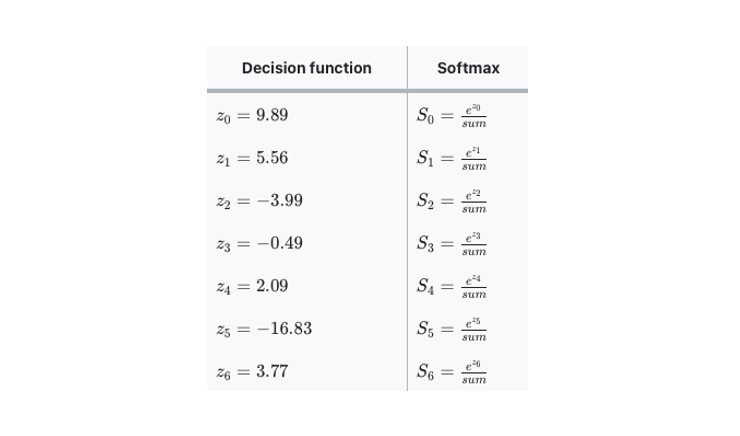
우리의 decisions 는 softmax 에 적용시켜보면 각각의 S값들은 그 결과가 앞서 실행한 predict_proba() 와 동일함을 알 수 있다.

from scipy.special import softmax

proba=softmax(decision, axis=1)
print(np.round(proba, decimals=3))

---