AI/ML/DL (3) - Evaluation metrics

Contents

1. Evaluation metrics
   1-1. Coefficient of determination
   1-2. Mean absolute error
   1-3. Mean squared error
   1-4. Root mean squared error

---

1. Evaluation metrics

The "score" method measures "accuracy" for classifiers, but regressors use various types of "metrics" to measure the deviation or error (e.g., R2, mae, mse, rmse).

1-1. Coefficient of determination

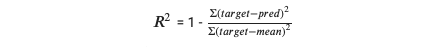
결정계수라 불리는 𝑅2 는 0 과 1 사이의 값을 return 하는데, 이때 𝑅2 가 1 에 가까울수록 더 좋은 모델임을 나타낸다. 위의 식을 참고해보자. 만약 모델의 prediction 이 평균과 같다면 분모와 분자가 거의 같아지므로 𝑅2 = 1-1 = 0 이 된다. 반면에 만약 prediction 이 target value 또는 실제값에 매우 가깝다면 𝑅2 = 1-0 = 1 로서 모델의 accuracy 를 증명한다.

1-2. Mean absolute error

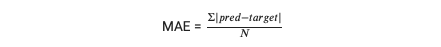
Mean absolute error, 또는 MAE, 는 실제값 (target value) 과 예측값 (prediction) 사이의 평균 거리를 나타내는데, 이때 N 은 data samples 의 전체 개수이다. MAE 는 실제값 또는 예측값들의 크기보다 errors 의 direction 과 consistency 를 고려할 때 주로 사용된다. 그러나 예측에 있어 large errors 를 다루기에는 무리가 있다. MAE 를 사용하기 위해 sklearn.metrics 에서는 다음과 같은 built-in function 을 제공한다.

from sklearn.metrics import mean_absolute_error

test_prediction = knr.predict(test_input)
mae = mean_absolute_error(test_target, test_prediction)
print(mae) # 35.50714285714285

1-3. Mean squared error

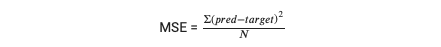
Mean squared error, 또는 MSE, 는 실제값과 예측값 사이 제곱차의 평균이다. MSE 는 regression models 의 performance 를 평가하기 위해 광범위하게 쓰이는데, 이는 linear regression, polynomial regression, and more 따위가 있다. MSE 가 작을수록 모델의 predictive accuracy 는 더 좋아진다.

1-4. Root mean squared error

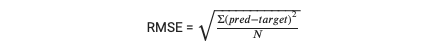
마지막으로 root mean squared error, 또는 RMSE, 는 각각의 예측값에 대해 실제값을 필요로 하기 때문에 supervised learning 에 흔히 사용되는 metric 이다.

---