👨‍🏫학습목표

오늘은 Actor-Critic Method의 구조와 TD Actor-Critic의 장점에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=l-9oSDKIaxg&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=23

1️⃣ Actor-Critic Method

📕 지난시간에 배운 내용

• DRL은 신경망을 통해 state-action value $Q(s,a)$ 나 policy $\pi(a|s)$ 를 근사하는 모델이다.

🔻 DRL의 종류

1. Deep Q-Network (DQN) : Value function $Q(s,a)$을 근사한다.

2. Policy Gradient (REINFORCE) : policy $\pi(a|s)$를 근사한다.

3. Actor-Critic (A3C) : Value function과 policy를 근사한다.

DQN과 REINFORCE에 대한 추가적인 내용은 아래 글에서 확인 가능하다.

📃DQN: https://velog.io/@tina1975/Deep-Reinforcement-Learning-17강-DQN-1

📃REINFORCE: https://velog.io/@tina1975/Deep-Reinforcement-Learning-22강-REINFORCE

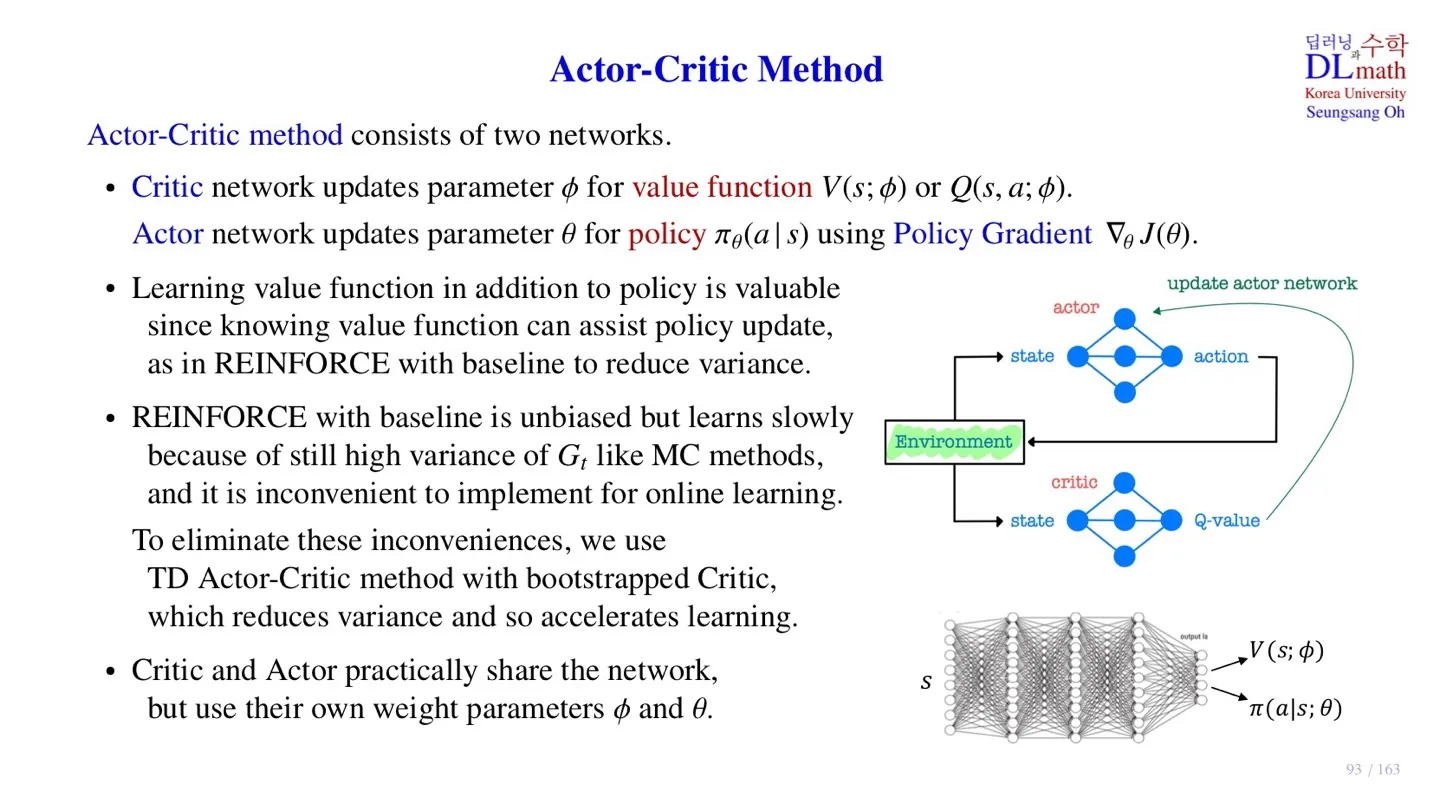
🔷 Actor-Critic Method

• Actor-Critic Method는 value function과 policy 2가지 값을 근사한다.

• 따라서 2가지 Network로 구성되어 있다.

• Critic Network$(\phi)$ : Value function $V(s; \phi) \ or \ Q(s,a ; \phi)$ 추정한다.

• Actor Network$(\theta)$ : Policy $\pi_{\theta}(a|s)$를 추정한다.

🔻 REINFORCE 모델의 특징

• REINFORCE 모델은 value function을 따로 출력한 후 value function을 업데이트 함으로써 모든 $Q(s,a)$를 동시에 업데이트하는 효과를 가진다.

• 파라미터를 업데이트 할 때 baseline을 빼줌으로써 sample data의 variance 역시 감소시킨다.

• Baseline을 빼주더라도 Bias가 발생하지 않는다.

• 하지만 여전히 return $G_t$의 variance가 크다는 한계가 존재한다.

• 또한 REINFORCE 모델을 업데이트하기 위해서는 하나의 episode를 종료 후 return $G_t$를 구하기 때문에, online 학습이 불가능하다.

🔸 REINFORCE와 TD Actor-Critid

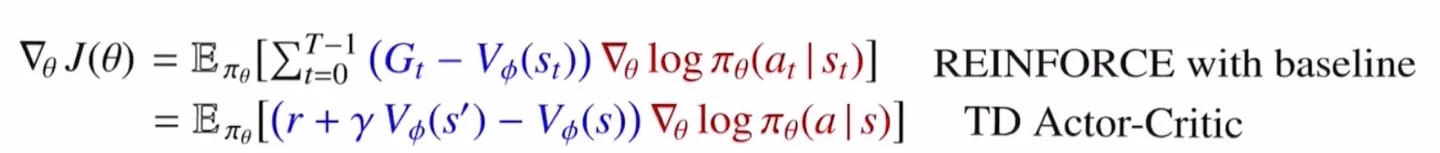
• REINFORCE 모델의 한계를 극복하기 위해 Temporal Difference Actor-Critic에서는 return $G_t$ 대신 temporal difference를 target으로 사용하여 업데이트를 진행한다.

• Temporal difference를 사용하기 때문에 하나의 episode가 아니라 다음 state에 대한 정보까지만을 활용한다.

• 그 결과 Online 학습이 가능해진다.

• 또한 Return $G_t$를 사용하지 않기 때문에 variance를 줄여 학습 속도를 높일 수 있다.

🔸 Monte Carlo와 temporal difference Learning

해당 자료에 대한 추가적인 내용은 아래 글에서 확인 가능하다.

📃링크: https://velog.io/@tina1975/Deep-Reinforcement-Learning-13강-Temporal-Difference-Learning-1

🔷 Actor-Critic Method 구조

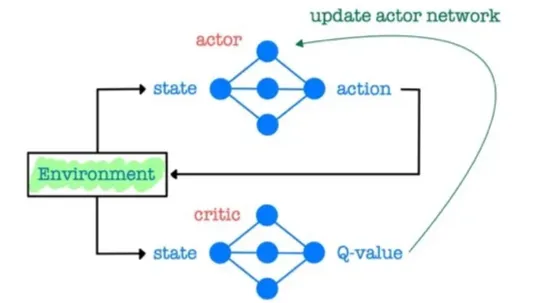
• Actor Network만 사용할 경우 policy gradient method와 유사하다.

• policy gradient method는 모델이 어떤 action을 취할 지 결정하는 policy $\pi$를 학습하는 모델이다.

• Actor-critic에서는 Critic Network를 통해 $V(s) \ or \ Q(s,a)$를 출력한다.

• 이 값을 통해 policy gradient를 업데이트할 때 도움을 준다.

• Actor Network에서 $\nabla_\theta \log \pi_\theta(a | s)$ 구한 후 Critic Network에서 구한 $r + \gamma V_\phi(s') - V_\phi(s)$를 활용하여 업데이트를 진행한다.

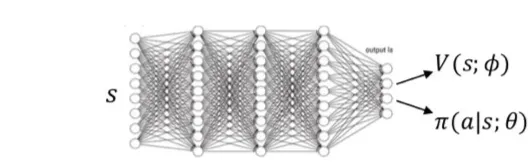
• Actor Network와 Critic Network 모두 대부분의 Network를 공유하지만, 모델마다 각자의 파라미터를 가지고 있는 경우 역시 존재한다.

---

2️⃣ Policy Gradient의 다양한 변형

🔷 Policy Gradient의 다양한 변형

🔻 1. REINFORCE (Monte Carlo PG)

$\nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}\left[\sum_{t=0}^{T-1} G_t \nabla_\theta \log \pi_\theta(a_t | s_t)\right]$

• 하나의 episode를 sample data로 사용하는 Monte Carlo 방식이다.
• Return $G_t$ 를 사용하기 때문에 variance가 크다.

🔻 2. REINFORCE with baseline

$\nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}\left[\sum_{t=0}^{T-1} (G_t - V_\phi(s_t)) \nabla_\theta \log \pi_\theta(a_t | s_t)\right]$

• Baseline을 사용하여 return $G_t$ 가 가지고있는 variance를 감소시킨다.
• Monte Carlo 방식은 하나의 episode를 target으로 하기 때문에 $\sum$ 로 이루어져 있다.

🔻 3. Q-value Actor-Critic

$\nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[Q_\phi(s, a) \nabla_\theta \log \pi_\theta(a | s)]$

• 자신이 추정한 $Q_{\phi}(s,a)$를 활용하여 업데이트를 진행하는 Bootstrap 방식을 사용한다.

🔻 4. Advantage Actor-Critic

$\nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[A_{\phi_1, \phi_2}(s, a) \nabla_\theta \log \pi_\theta(a | s)]$

• 자신이 추정한 $A_{\phi_1, /\phi_2}(s,a)$를 활용하여 업데이트를 진행하는 Bootstrap 방식을 사용한다.

🔻 5. TD Actor-Critic

$\nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[(r + \gamma V_\phi(s') - V_\phi(s)) \nabla_\theta \log \pi_\theta(a | s)]$

• 자신이 추정한 $r + \gamma V_\phi(s') - V_\phi(s)$ 를 활용하여 업데이트를 진행하는 Bootstrap 방식을 사용한다.

• 파란색 부분을 Critic, 빨간색 부분을 Actor라고 부른다.
• 사용하는 Critic에 따라 Actor-Critic의 이름이 바뀐다.
• 다양한 변형이 있지만 Expectation 값이 바뀌지 않는다.

🔷 Policy Gradient의 다양한 변형이 가능한 이유

1. REINFORCE 모델은 Return $G_t$ 를 사용하기 때문에 variance가 크다.

2. 이를 해결하기 위해 Baseline으로 $V_{\phi}(s_t)$를 빼줌으로써 variance를 줄인다. 이때 $V_{\phi}(s_t)$는 action과 관계가 없어 expectation 값에 영향을 주지 않는다.

3. TD Actor-Critic (5번째 모델)에서는 Return $G_t$ 대신 $r + \gamma V_\phi(s')$ 즉 1-step return을 사용한다. 이때 $G_t^{(1)} \approx G_t$ 하기 때문에 expectation 값이 유지된다.

4. $E[R_{t+1} + \gamma V^{\pi_\theta}_\phi(S_{t+1})] \approx E[Q_{\phi_2}(s,a)]$ 이므로 Q-value Actor-Critic 역시 expectation을 만족한다.

5. 마지막으로 Advantage Actor-Critic은 Q-value Actor-Critic에서 baseline을 추가한 모델이다. 따라서 Expectation의 변화가 없다.

🔻 TD Actor-Critic을 사용하는 이유

• Q-value Actor-Critic과 Advantage Actor-Critic을 사용하기 위해서는 각 action의 Q-value 값을 알아야 하는데 이는 쉽지 않다.

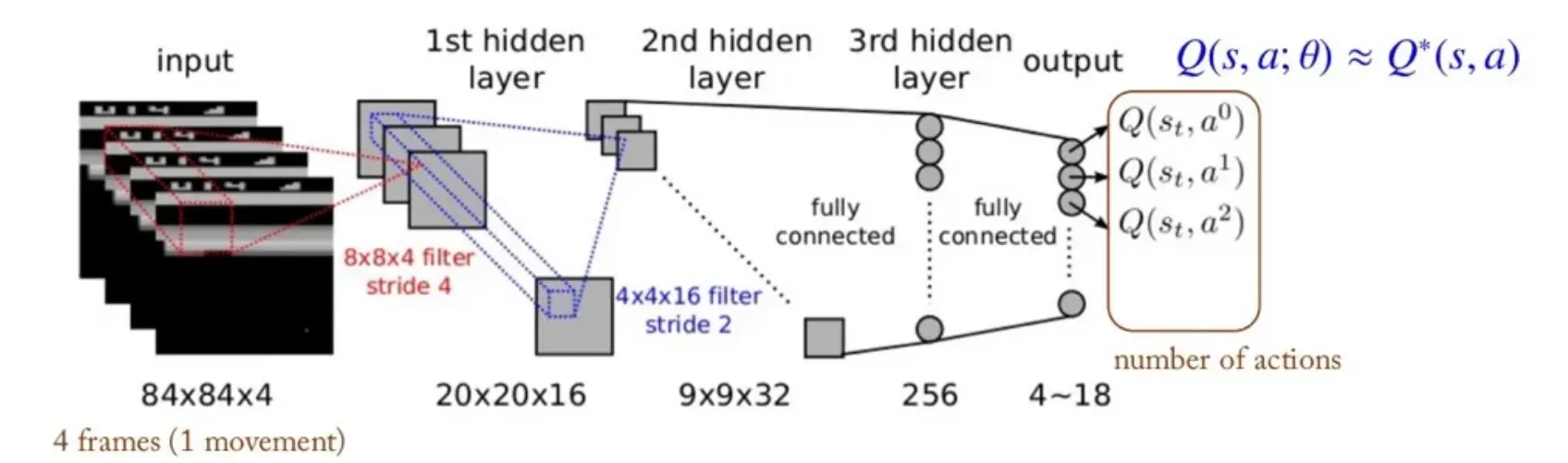
• Q-value값을 출력할 경우 $a_0$와 $a_1$ 사이의 continuous한 action을 표현할 수 없다.
• 하지만 TD Actor-Critic는 state function 값만 알면 되기 때문에 가장 구현하기 쉽다.

---

3️⃣ Critic Network와 Actor Network

🔷 Critic Network의 Loss function

$\text{minimizing } L(\phi) = \text{MSE}(\text{target} - V_\phi(s_t))^2$

• Target값과 가까워지도록 학습한다.
• 이때 target은 MC방식과 TD방식으로 나뉠 수 있다.

$\phi := \phi + \beta (\text{target} - V_\phi(s_t)) \nabla_\phi V_\phi(s_t)$

• Loss function을 미분 후 gradient descent 방식으로 파라미터를 업데이트한다.

🔻MC target $G_t$

$\Delta\phi = \beta(G_t - V_\phi(s_t)) \nabla_\phi V_\phi(s_t)$

🔸 Pseudo Code

$\delta \leftarrow G_t - V(s_t; \phi)$

$\phi \leftarrow \phi + \beta \delta \nabla_\phi V(s_t; \phi)$

🔻TD target $r + \gamma V_\phi(s')$

$\Delta\phi = \beta(r_{t+1} + \gamma V_\phi(s_{t+1}) - V_\phi(s_t)) \nabla_\phi V_\phi(s_t)$

🔸 Pseudo Code

$\delta \leftarrow r + \gamma V(S_{t+1}; \phi) - V(s_t; \phi)$

$\phi \leftarrow \phi + \beta \delta \nabla_\phi V(s_t; \phi)$

🔷 Actor Network의 Object function

$\text{maximizing } J(\theta) = \mathbb{E}[r(\tau)]$

• Total Reward의 expectation을 maximize하는 방향으로 학습한다.

$\theta := \theta + \alpha \nabla_\theta \mathbb{E}[r(\tau); \theta]$

• Object function을 미분 후 gradient ascent 방식으로 파라미터를 업데이트한다.

🔻MC policy gradient update

$\Delta\theta = \alpha (G_t - V_\phi(s_t)) \nabla_\theta \log \pi_\theta(a_t | s_t)$

🔸 Pseudo Code

$\theta \leftarrow \theta + \alpha \gamma' \delta \nabla_\theta \log \pi(a_t | s_t; \theta)$

🔻TD policy gradient update

$\Delta\theta = \alpha (r_{t+1} + \gamma V_\phi(s_{t+1}) - V_\phi(s_t)) \nabla_\theta \log \pi_\theta(a_t | s_t)$

🔸 Pseudo Code

$\theta \leftarrow \theta + \alpha \gamma^t \delta \nabla_\theta \log \pi(a_t | s_t; \theta)$

---

4️⃣ Actor-Critic Method의 pseudo code

🔻 Network 초기화

• Critic Network $V(s; \phi)$ 와 Actor Network $Q(s,a ; \phi)$의 파라미터를 초기화한다.
• 학습률 역할을 수행하는 step size $\alpha, \beta$ 값을 초기화한다.

🔻 Sample data 수집

• 초기 state 를 선택한다.
• Actor Network가 추정한 Policy $\pi_{\theta}(a|s)$를 통해 action을 선택한다.
• 해당 action을 실제로 수행하여 $r'$ 과 $s'$ 을 얻는다.
• $(s_t, a_t, r_{t+1}, s_{t+1})$ 단위로 sample 데이터를 수집한다.

🔻 파라미터 업데이트

$\delta \leftarrow r + \gamma V(S_{t+1}; \phi) - V(s_t; \phi)$

• Temporal Difference error $\delta$를 계산한다.

$\phi \leftarrow \phi + \beta \delta \nabla_\phi V(s_t; \phi)$

• Cricit Network의 Loss function을 미분하여 파라미터를 업데이트한다.

$\theta \leftarrow \theta + \alpha \gamma^t \delta \nabla_\theta \log \pi(a_t | s_t; \theta)$

• Actor Network의 Object function을 미분하여 파라미터를 업데이트한다.

---

5️⃣ 정리

🔷 23강에서 배운 내용은 아래와 같다.

1. Critic-Actor Method에는 Critic Network와 Action Network가 존재한다.
2. Critic Network는 학습의 크기를 조정하는 value function을 추정한다.
3. Actor Network는 학습의 방향을 결정하는 policy를 학습한다.
4. TD Actor-Critic 모델이 가장 구현하기 쉽다.
5. TD Actor-Critic의 pseudo code를 살펴보았다.