Predict the future from the past with a lag embedding.

What is Serial Dependence?

전 강의에서는 시간 종속 속성, 즉 시간 지수에서 직접 도출할 수 있는 특징을 사용하여 가장 쉽게 모델링할 수 있는 시계열의 속성에 대해 살펴보았다.
그러나 일부 시계열 속성은 시계열 종속 속성으로만 모델링할 수 있다.
즉 대상 시계열의 과거 값을 피처로 사용하는 것이다.
이러한 시계열의 구조는 시간 경과에 따른 플롯에서는 명확하지 않을 수 있지만, 아래 그림에서 볼 수 있듯이 과거 값에 대해 플롯하면 구조가 명확해진다.

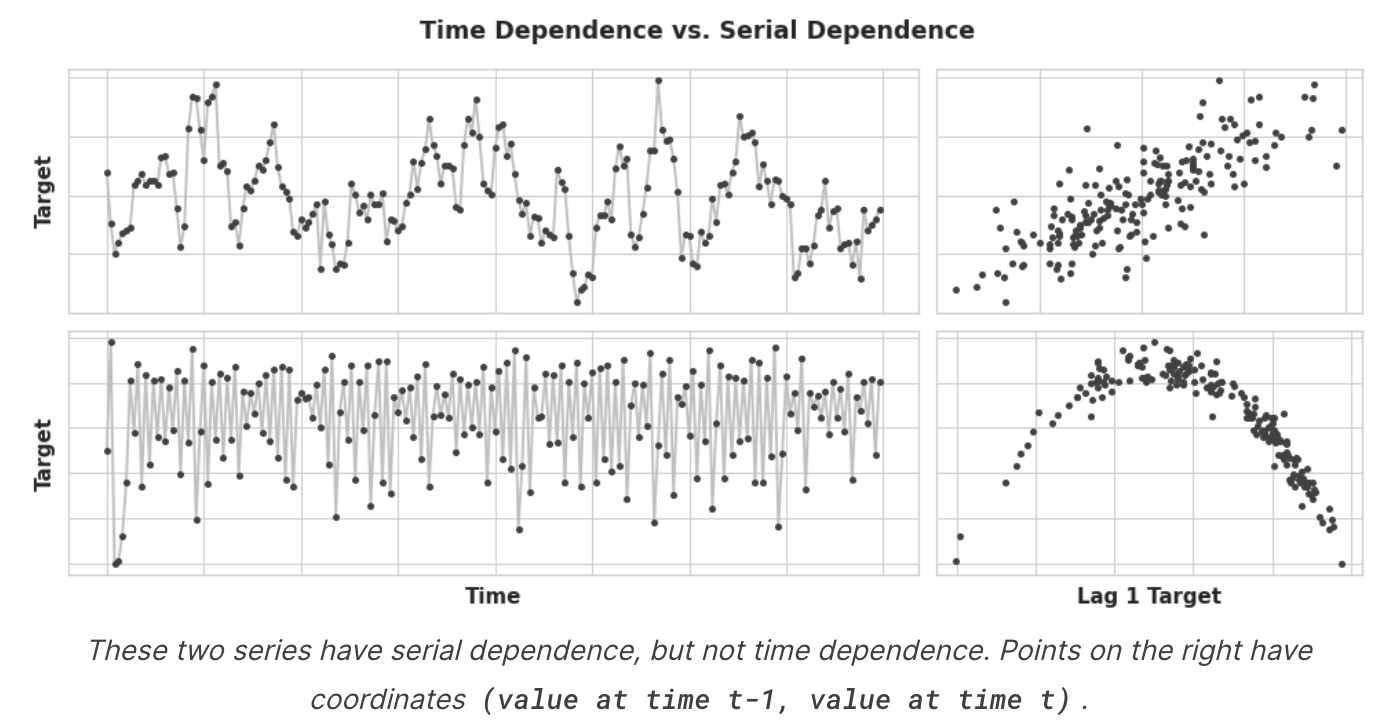
Trend와 Seasonality를 사용하여 위 그림의 왼쪽과 같은 plot에 곡선을 맞추도록 훈련시켰다. 이 모델은 시간 의존성을 학습하고 있었다. 이 단원의 목표는 모델이 오른쪽 그림과 같은 plot에 곡선을 맞추도록 훈련하는 것이다. 즉, 모델이 직렬 의존성을 학습하도록 하려는 것이다.

Cycles

특히 직렬 의존성이 나타는 일반적인 방법 중 하나는 Cycles이다. 주기(Cycles)는 한 시점의 시계열 값이 이전 시점의 값에 의존하는 방식과 관련된 시계열의 성장 및 쇠퇴 패턴이지만, 반드시 time step 자체에 의존하는 것은 아니다. 순환적 행동은 스스로 영향을 미칠 수 있거나 시간이 지나도 반응이 지속되는 시스템이다. 경제, 전염병, 동물 개체 수, 화산 폭발 및 이와 유사한 자연 현상은 종종 주기적 행동을 보인다.

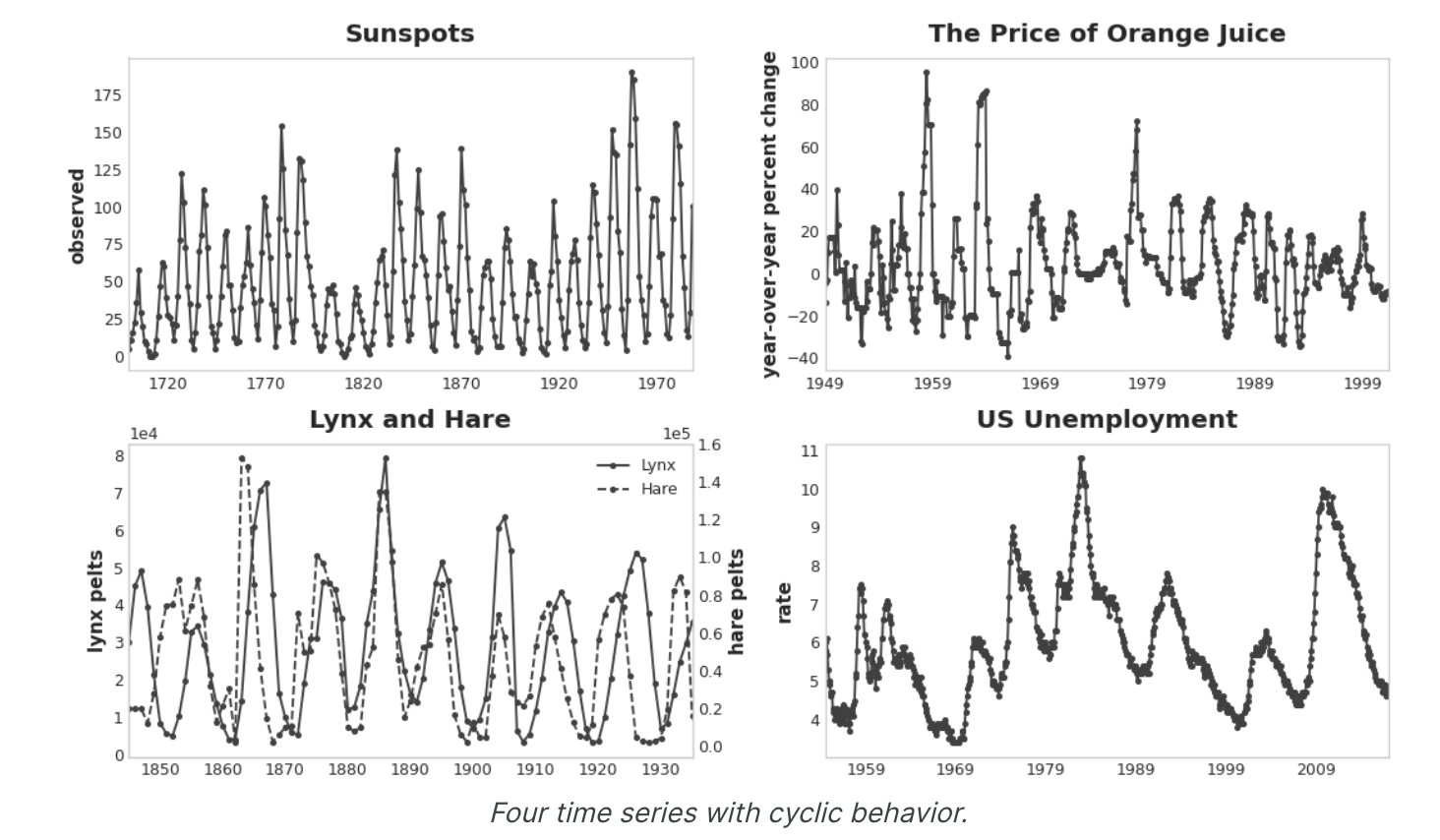
주기적 행동이 계절성과 구별되는 점은 계절처럼 주기가 반드시 시간에 의존하지 않는다는 점이다. 주기에서 일어나는 일은 특정 발생 날짜보다는 최근 과거에 일어난 일에 더 큰 영향을 받는다. 시간으로부터(적어도 상대적으로) 독립적이라는 것은 주기적 행동이 계절성보다 훨씬 더 불규칙할 수 있다는 것을 의미한다.

Lagged Series and Lag Plots

시계열에서 가능한 직렬 의존성(Cycles 같은)을 조사하려면 시계열의 "지연된" 복사본을 만들어야 한다. 시계열을 지연시킨다는 것은 그 값을 하나 이상의 시간 단계 앞으로 이동하거나, 이와 동등하게 인덱스의 시간을 하나 이상의 시간 단계 뒤로 이동하는 것을 의미한다.
두 경우 모두 시차가 있는 시계열의 관측값이 나중에 발생한 것처럼 보이게 되는 효과가 있다.
다음은 미국의 월별 실업률(y)과 그 첫 번째 및 두 번째 시차 계열(각각 y_lag_1 및 y_lag_2)을 함께 보여준다. 시차가 있는 시계열의 값이 어떻게 시간이 앞으로 이동하는지 주목해보자..

import pandas as pd

# Federal Reserve dataset: https://www.kaggle.com/federalreserve/interest-rates
reserve = pd.read_csv(
    "../input/ts-course-data/reserve.csv",
    parse_dates={'Date': ['Year', 'Month', 'Day']},
    index_col='Date',
)

y = reserve.loc[:, 'Unemployment Rate'].dropna().to_period('M')
df = pd.DataFrame({
    'y': y,
    'y_lag_1': y.shift(1),
    'y_lag_2': y.shift(2),    
})

df.head()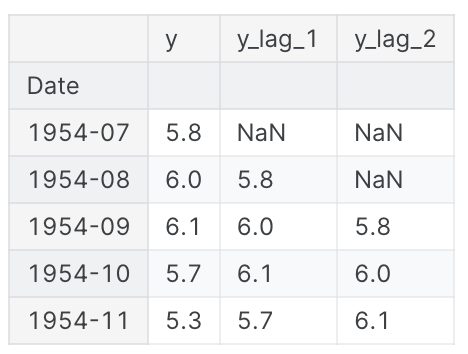

시계열에 시차를 두면 과거 값이 예측하려는 값과 동시적으로(즉, 같은 행에) 나타나도록 할 수 있다. 따라서 시차가 있는 시계열은 직렬 의존성을 모델링하는 데 유용하다. 미국의 실업률 시리즈를 예측하기 위해 y_lag_1과 y_lag_2를 feature로 사용하여 목표 y를 예측하면 이전 2개월의 실업률의 함수로 미래 실업률을 예측할 수 있다.

Lag plots

시계열의 Lag plot은 그 값을 지연에 대해 plot한 것이다. 시계열의 직렬 의존성은 종종 지연 plot을 보면 분명해진다. 이 미국의 실업률의 지연 플롯을 보면 현재 실업률과 과거 실업률 사이에 강력하고 명백한 선형 관계가 있음을 알 수 있다.

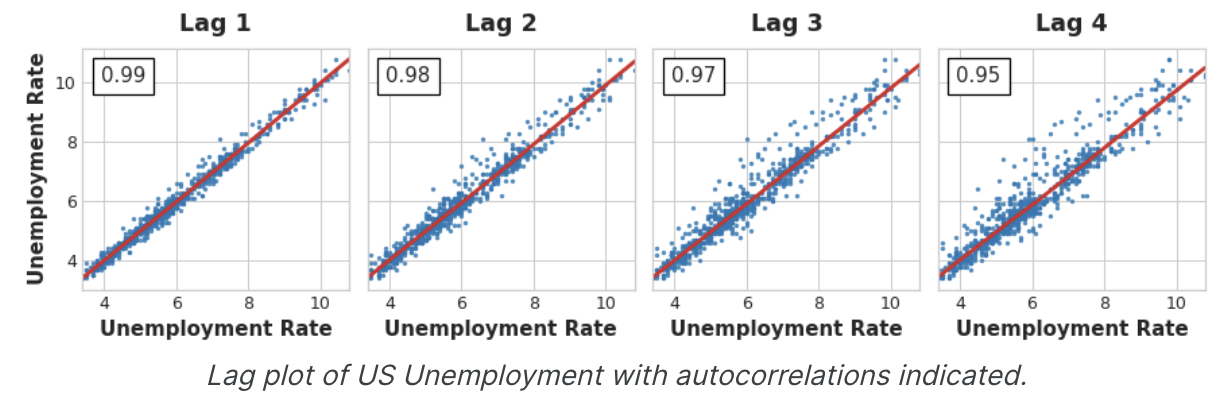
가장 일반적으로 사용되는 직렬 의존성의 척도는 자상 관계로 알려져있으며, 이는 단순히 시계열이 시차 중 하나와 갖는 상관관계이다. 미국 실업률은 시차 1에서 0.99, 시차 2에서 0.98 등의 자상관계가 있다.

Autocorrelation (자기 상관)
자기들끼리의 상관 관계를 의미, lag된 값들과의 관계를 의미한다.

Choosing lags

feature로 사용할 lag을 선택할 때 일반적으로 자기 상관관계가 큰 모든 lag을 포함하는 것은 유용하지 않다. 예를 들어, 미국 실업률에서 lag2의 자기 상관관계는 전적으로 lag1의 '붕괴된' 정보, 즉 이전 단계에서 이월된 상관관계에서 비롯된 것일 수 있다. lag2에 새로운 정보가 포함되어 있지 않다면 이미 lag1이 있는 경우 이를 포함할 이유가 없음.

부분 자동 상관관계(partial autocorrelation)은 이전 모든 lag을 설명하는 lag의 상관관계, 즉 lag이 기여하는 "새로운" 상관관계의 양을 알려준다. 부분 자동상관관계를 plotting하면 어떤 lag geature를 사용할지 선택하는 데 도움이 될 것이다.
아래 그림에서 lag1부터 la6g까지는 '상관관계 없음' 구간(파란색)을 벗어나 있으므로 lag1부터 lag6까지를 미국 실업률의 특징으로 선택할 수 있다.(lag11은 오탐일 가능성이 있음)

위와 같은 plot을 '상관도(correlogram)'라고 한다. 이는 본질적으로 fourier feature에 대한 주기 도표와 같은 lag feature에 대한 것이다.

마지막으로, 자기상관과 부분 자기상관은 선형 의존성의 척도라는 것을 염두에 두어야 한다. 실제 시계열에서는 상당한 비선형 의존성이 있는 경우가 많으므로 lag feature를 선택할 때는 lag plot을 보거나 상호 정보와 같은 보다 일반적인 의존성 측정값을 사용하는 것이 좋다. 태양 흑점 계열에는 비선형 의존성을 가진 지연이 있는데, 이는 자기상관으로 간과할 수 있다.

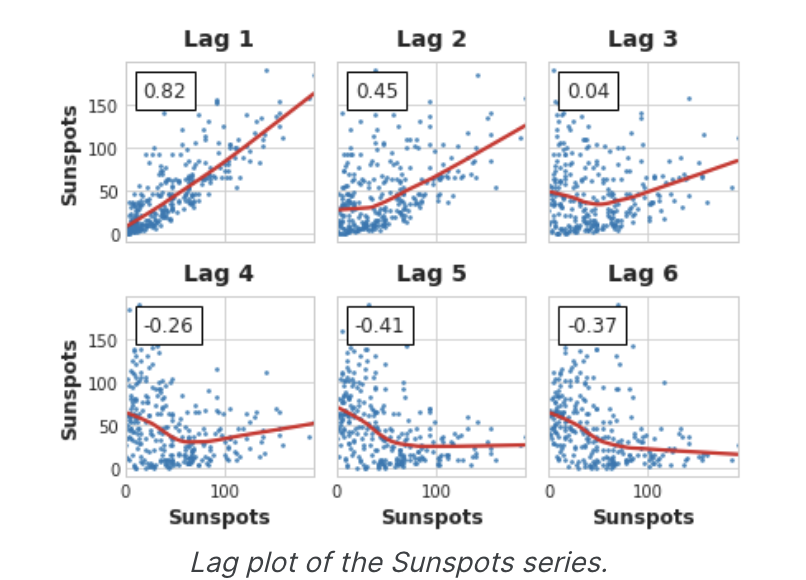
이와 같은 비선형 관게는 선형 관계로 변환하거나 적절한 알고리즘을 통해 학습할 수 있다.

Example - Flu Trends

독감 동향 데이터 셋에는 2009년부터 2016년까지 몇 주 동안의 독감으로 인한 의사 방문 기록이 포함되어 있다. 우리의 목표는 앞으로 몇 주 동안의 독감 발병 건수를 예측하는 것이다.

두 가지 접근 방식을 취할 것이다.
1. Lag Feature
2. Use another time series(구글 트렌드)

from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.signal import periodogram
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from statsmodels.graphics.tsaplots import plot_pacf

simplefilter("ignore")

# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 4))
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
)
%config InlineBackend.figure_format = 'retina'


def lagplot(x, y=None, lag=1, standardize=False, ax=None, **kwargs):
    from matplotlib.offsetbox import AnchoredText
    x_ = x.shift(lag)
    if standardize:
        x_ = (x_ - x_.mean()) / x_.std()
    if y is not None:
        y_ = (y - y.mean()) / y.std() if standardize else y
    else:
        y_ = x
    corr = y_.corr(x_)
    if ax is None:
        fig, ax = plt.subplots()
    scatter_kws = dict(
        alpha=0.75,
        s=3,
    )
    line_kws = dict(color='C3', )
    ax = sns.regplot(x=x_,
                     y=y_,
                     scatter_kws=scatter_kws,
                     line_kws=line_kws,
                     lowess=True,
                     ax=ax,
                     **kwargs)
    at = AnchoredText(
        f"{corr:.2f}",
        prop=dict(size="large"),
        frameon=True,
        loc="upper left",
    )
    at.patch.set_boxstyle("square, pad=0.0")
    ax.add_artist(at)
    ax.set(title=f"Lag {lag}", xlabel=x_.name, ylabel=y_.name)
    return ax


def plot_lags(x, y=None, lags=6, nrows=1, lagplot_kwargs={}, **kwargs):
    import math
    kwargs.setdefault('nrows', nrows)
    kwargs.setdefault('ncols', math.ceil(lags / nrows))
    kwargs.setdefault('figsize', (kwargs['ncols'] * 2, nrows * 2 + 0.5))
    fig, axs = plt.subplots(sharex=True, sharey=True, squeeze=False, **kwargs)
    for ax, k in zip(fig.get_axes(), range(kwargs['nrows'] * kwargs['ncols'])):
        if k + 1 <= lags:
            ax = lagplot(x, y, lag=k + 1, ax=ax, **lagplot_kwargs)
            ax.set_title(f"Lag {k + 1}", fontdict=dict(fontsize=14))
            ax.set(xlabel="", ylabel="")
        else:
            ax.axis('off')
    plt.setp(axs[-1, :], xlabel=x.name)
    plt.setp(axs[:, 0], ylabel=y.name if y is not None else x.name)
    fig.tight_layout(w_pad=0.1, h_pad=0.1)
    return fig


data_dir = Path("../input/ts-course-data")
flu_trends = pd.read_csv(data_dir / "flu-trends.csv")
flu_trends.set_index(
    pd.PeriodIndex(flu_trends.Week, freq="W"),
    inplace=True,
)
flu_trends.drop("Week", axis=1, inplace=True)

ax = flu_trends.FluVisits.plot(title='Flu Trends', **plot_params)
_ = ax.set(ylabel="Office Visits")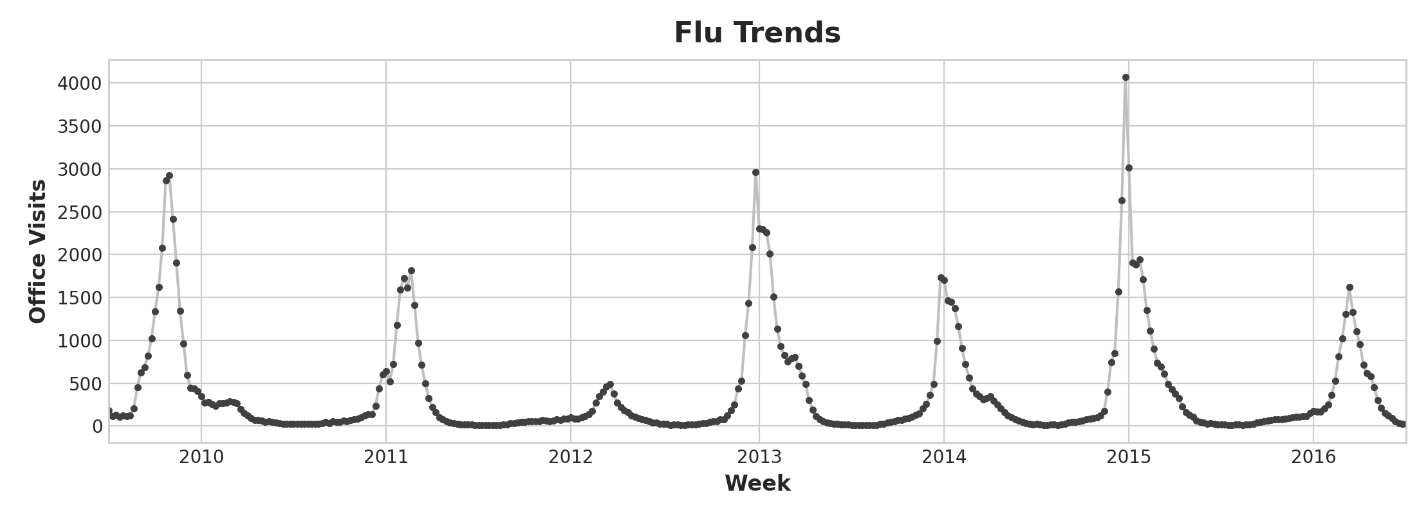

독감 트렌드 데이터는 규칙적인 계절성 대신 불규칙한 주기를 보여준다. 새해 즈음에 정점에 도달하는 경향이 있지만 떄로는 더 빠르거나 늦게, 때로는 더 크거나 작게 나타난다. 이러한 주기를 lag feature를 통해 모델링하면 예측자가 계절 feature 처럼 정확한 날짜와 시간에 제약을 받지 않고 변화하는 상황에 동적으로 대응할 수 있다.

lag과 자기 상관 plot을 살펴보자.

_ = plot_lags(flu_trends.FluVisits, lags=12, nrows=2)
_ = plot_pacf(flu_trends.FluVisits, lags=12)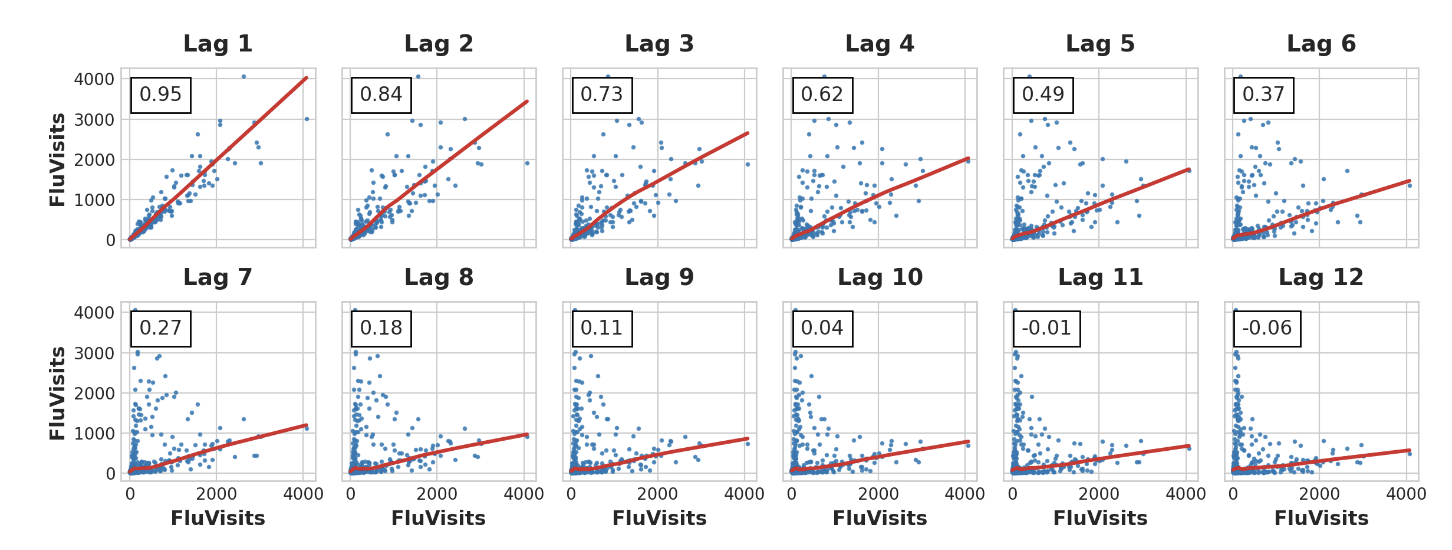

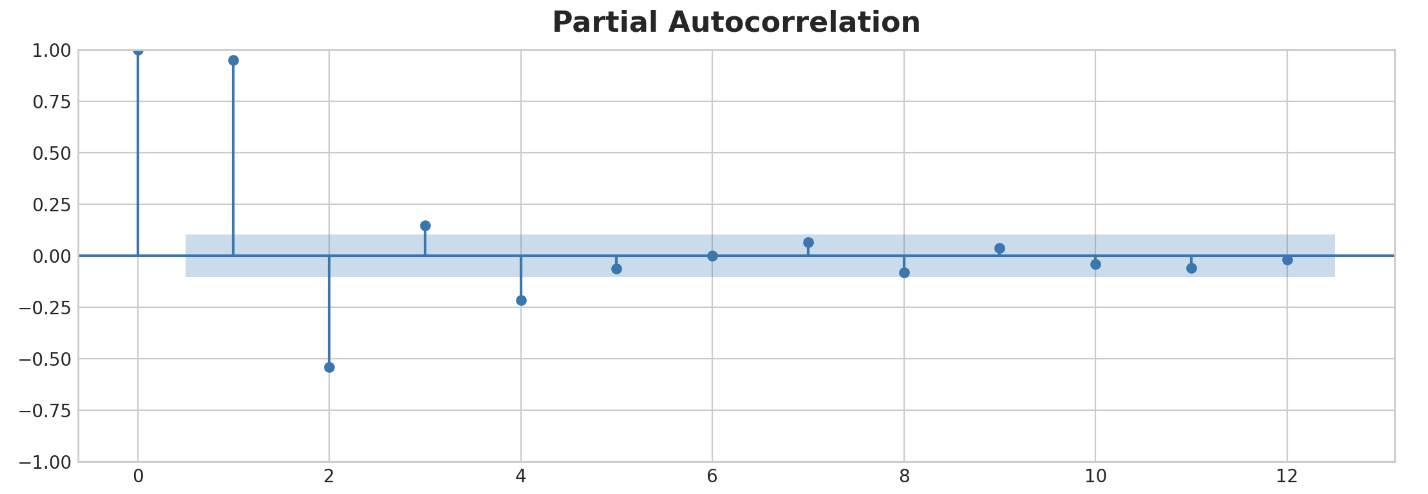
lag plot은 FluVisits와 그 지연 관계가 대부분 선형임을 나타내며, 부분 자기 상관은 lag1, 2, 3, 4를 사용하여 의존성을 포착할 수 있음을 시사한다. shift method를 사용하면 pandas에서 시계열을 지연시킬 수 있다. 이 문제에서는 lag으로 생기는 결측값을 0.0으로 채울 것

def make_lags(ts, lags):
	return pd.concat(
    	{
        	f'y_lag_{i}': ts.shift(i)
            for i in rage(1, lags + 1)
        },
        axis=1)
      
X = make_lags(flu_trends.FluVisits, lags=4)
X = X.fillna(0.0)

이전 강의에서는 학습 데이터를 넘어 원하는 만큼 많은 단계에 대한 예측을 만들 수 있었다. 그러나 lag features를 사용할 때는 지연된 값을 사용할 수 있는 시간 단계만 예측할 수 있다.
월요일에 lag1 기능을 사용하면 필요한 lag1 값은 아직 발생하지 않은 화요일이므로 수요일에 대한 예측을 만들 수 없다.

이 상황에 대해서는 6강에서 알려준다네요..
여기서는 테스트셋만!

y = flu_trends.FluVisits.copy()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=60, shuffle=False)

# Fit and predict
model = LinearRegression() # 'fit_intercept=True' since we didn't use DeterministicProcess
model.fit(X_train, y_train)
y_pred = pd.Series(model.predict(X_train), index=y_train.index)
y_fore = pd.Series(model.predict(X_test), index=y_test.index)

ax = y_train.plot(**plot_params)
ax = y_test.plot(**plot_params)
ax = y_pred.plot(ax=ax)
_ = y_fore.plot(ax=ax, color='C3')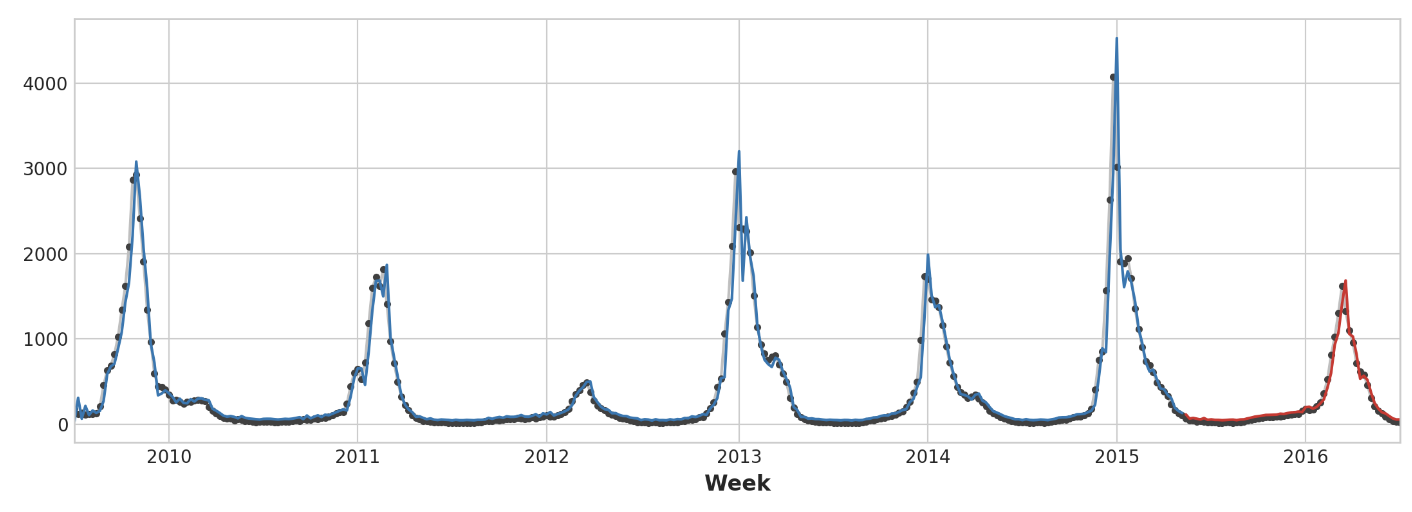

예측 값만 보면 대상 계열의 갑작스러운 변화에 반응하기 위해 모델의 time step이 필요하다는 것을 알 수 있다. 이는 대상 계열의 지연만을 특징으로 사용하는 모델의 일반적인 한계이다.

ax = y_test.plot(**plot_params)
_ = y_fore.plot(ax=ax, color='C3')

예측을 개선하기 위해 독감 사례의 변화에 대한 '조기 경보'를 제공할 수 있는 시계열인 선행 지표를 찾을 수 있다. 두 번째 접근 방식에서는 Google Trends에서 측정한 일부 독감 관련 검색어의 인기도를 학습 데이터에 추가한다.

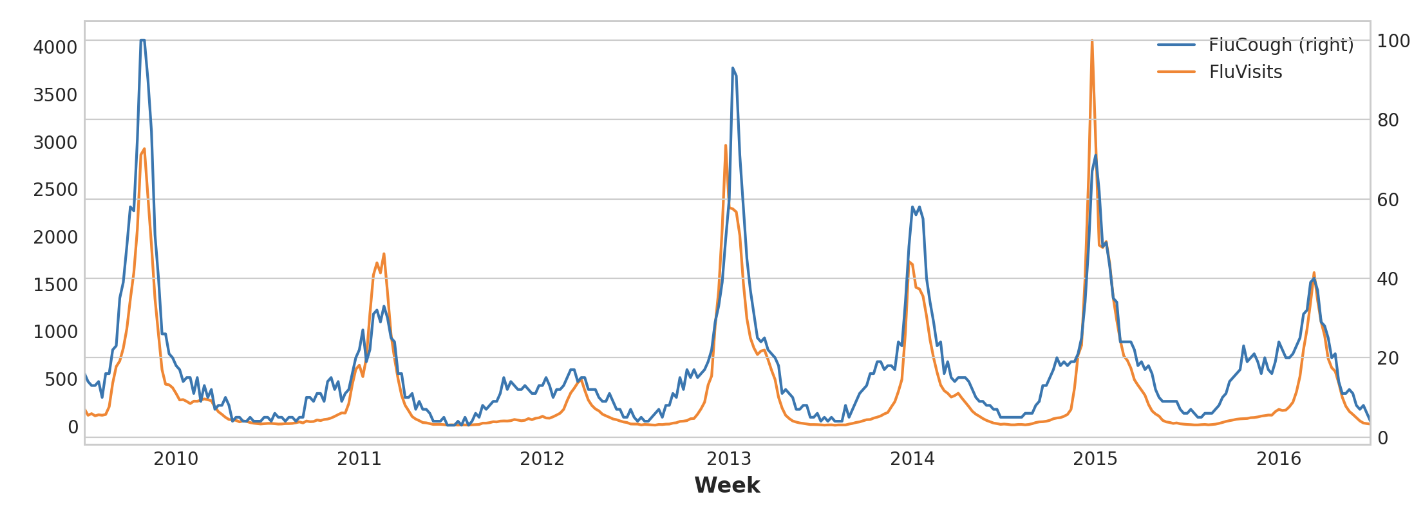
FluCough라는 검색어를 FluVisits에 plot하면 이러한 검색어가 선행 지표로 유용할 수 있음을 알 수 있다. 독감 관련 검색은 병원 방문 전 주에 더 인기가 높아지는 경향이 있다.

ax = flu_trends.plot(
	y=["FluCough", "FluVisitors"],
    secondary_y="FluCough",
)

데이터 셋에서는 129개의 용어가 있지만 여기서는 몇 개만 사용

search_terms = ["FluContagious", "FluCough", "FluFever", "InfluenzaA", "TreatFlu", "IHaveTheFlu", "OverTheCounterFlu", "HowLongFlu"]

# Create three lags for each search term
X0 = make_lags(flu_trends[search_terms], lags=3)
X0.columns = [' '.join(col).strip() for col in X0.columns.values]

# Create four lags for the target, as before
X1 = make_lags(flu_trends['FluVisits'], lags=4)

# Combine to create the training data
X = pd.concat([X0, X1], axis=1).fillna(0.0)

예측은 다소 거칠지만 독감 방문의 급격한 증가를 더 잘 예측하는 것으로 보아 여러 시계열의 검색 인기도가 선행 지표로서 효과적임을 알 수 있음.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=60, shuffle=False)

model = LinearRegression()
model.fit(X_train, y_train)
y_pred = pd.Series(model.predict(X_train), index=y_train.index)
y_fore = pd.Series(model.predict(X_test), index=y_test.index)

ax = y_test.plot(**plot_params)
_ = y_fore.plot(ax=ax, color='C3')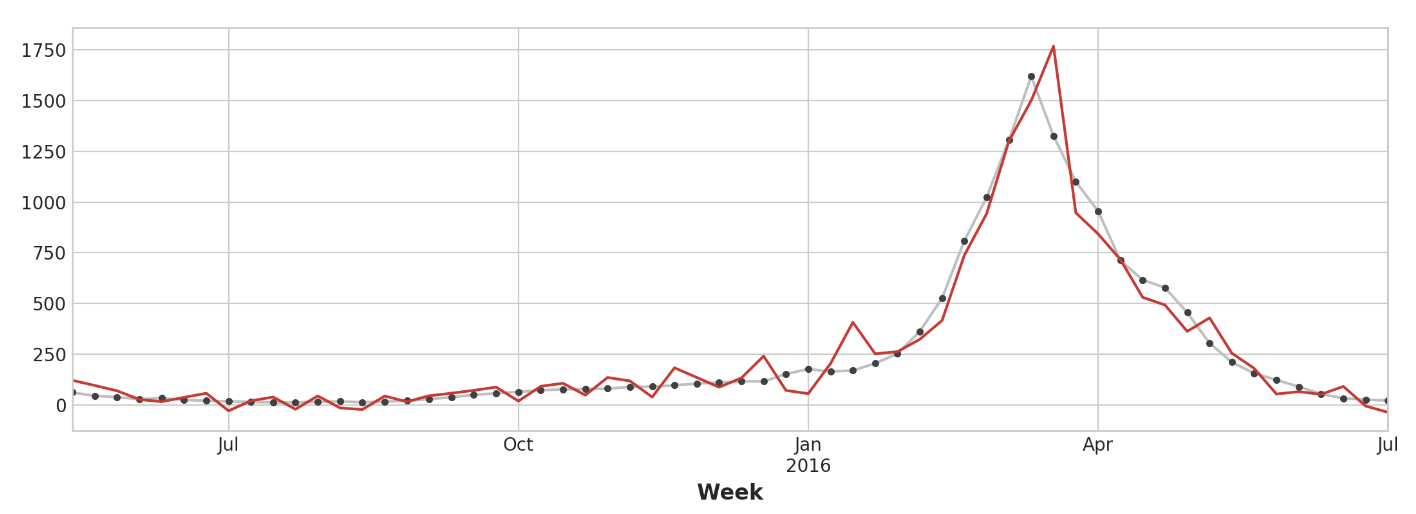

이 단원에서 설명하는 시계열은 "순수 주기적" 이라고 할 수 있는 것으로, 뚜렷한 추세나 계절성이 없다. 하지만 추세, 계절성, 주기라는 세 가지 요소를 한 번에 모두 포함하는 시계열은 흔하다. 각 구성 요소에 적절한 기능을 추가하기만 하면 선형 회귀를 통해 이러한 시계열을 모델링할 수 있다. 구성 요소를 개별적으로 학습하도록 훈련된 모델을 결합할 수도 있는데, 다음 단원에서 예측 하이브리드를 통해 알아보자~