
작성자 : 광운대학교 전자통신공학과 신민정
Generative Modeling
생성모델링은 가지고있는 데이터 분포에서 sampling한 것 같은 새로운 데이터를 만드는 것입니다.
생성모델링은 판별모델링과 비교하면 이해하기 쉽습니다. 판별모델링은 label y가 필요한 supervised learning이고, 생성모델링은 label y가 필요없는 unsupervised learning입니다. [label y가 있는 경우도 존재]
- 판별모델링 : Sample x가 주어졌을 때, label y의 확률 를 추정
- 생성모델링 : Sample x의 를 추정,
[ label이 있는 경우(with condition vector)는 를 추정(아래 CGAN에서 설명) ]
생성모델링의 목적 : Want to learn similar to
 [출처 : 미술관에서 GAN 딥러닝 실전프로젝트 ]
[출처 : 미술관에서 GAN 딥러닝 실전프로젝트 ]
 [출처 : NaverD2 "Generative adversarial Networks" 최윤제님 강의자료]
[출처 : NaverD2 "Generative adversarial Networks" 최윤제님 강의자료]
GAN의 구조
GAN이란 Generativ Adversarial Network의 약자입니다.
한국어로 풀어쓴다면 '생성적 적대 신경망'이고, 단어 그대로를 해석한다면 새로운 데이터를 생성하기 위해 뉴럴네트워크로 이루어진 생성자(Generator)와 판별자(Discriminator)가 서로 겨루며 훈련한다는 뜻입니다.
생성자(Generator,이하 G)와 판별자(Discriminator,이하 D)의 역할과 동작을 알아보겠습니다.
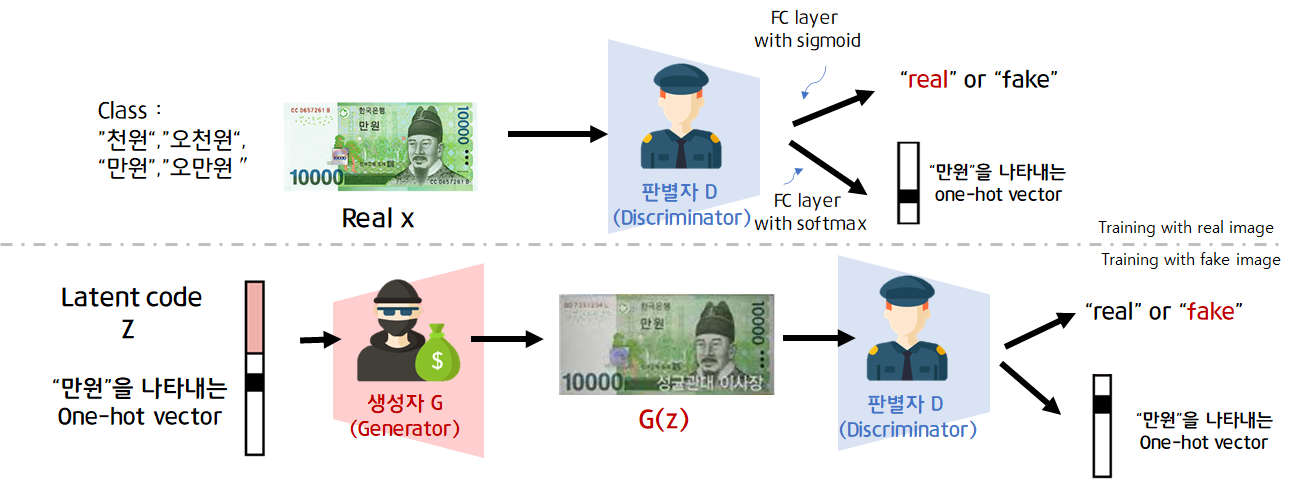
 GAN의 원본 논문에서는 판별자와 생성자를 경찰과 위조지폐범으로 표현했습니다. 판별자 D는 진짜 화폐(dataset의 x)와 생성자가 만들어낸 가짜 화폐를 "real"or"fake"를 잘 구분해야 합니다. 생성자 G는 진짜 화폐같은 가짜 화폐를 만듭니다.
GAN의 원본 논문에서는 판별자와 생성자를 경찰과 위조지폐범으로 표현했습니다. 판별자 D는 진짜 화폐(dataset의 x)와 생성자가 만들어낸 가짜 화폐를 "real"or"fake"를 잘 구분해야 합니다. 생성자 G는 진짜 화폐같은 가짜 화폐를 만듭니다.
| 생성자 Generator | 판별자 Discriminator | |
|---|---|---|
| 입력 | 랜덤한 숫자로 구성된 벡터z | 1. 훈련 데이터셋에 있는 실제 샘플 x, 2. 생성자가 만든 가짜 샘플 z |
| 출력 | 최대한 진짜 같이 보이는 가짜 샘플G(z) | 입력 샘플이 진짜일 예측 확률 |
| 목표 | 훈련 데이터셋에 있는 샘플x과 구별이 불가능한 가짜 샘플G(z) 생성하기 | 생성자가 만든 가짜 샘플G(z)과 훈련 데이터셋의 진짜 샘플x 구별하기 |
판별자 Discriminator를 먼저 학습합니다. 진짜 이미지x가 들어가면 진짜(1)로 구분, 가짜이미지(생성자가 random code를 받아 만들어낸 G(z))를 입력으로 받으면 가짜(0)로 구분해야합니다. output layer에는 sigmoid를 activation function으로 사용합니다.(0.5를 가준으로 real or fake binary classification)
생성자 Gernerator는 random code z를 입력으로 받아 진짜 이미지 x와 유사한 이미지를 생성합니다. 생성자 G가 잘 학습된다면 D(G(z))가 1에 가까운 값이 나오게됩니다.
LOSS
GAN의 판별자 D는 real or fake를 판단하기 때문에, Binary Cross Entropy(이하BCE)를 사용합니다
[real일 때 y = 1, fake일 때 y = 0인 이진분류]
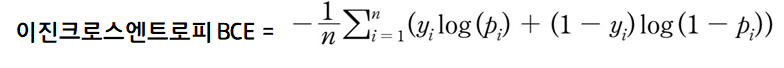
아래의 식은 BCE를 GAN에 적용했을 때의 Loss입니다.
x~P_{data}(x) : 실제 데이터 분포에서 온 sample x
z~P_{x}(x) : Gaussian 분포(예)에서 온 Sample latent code z
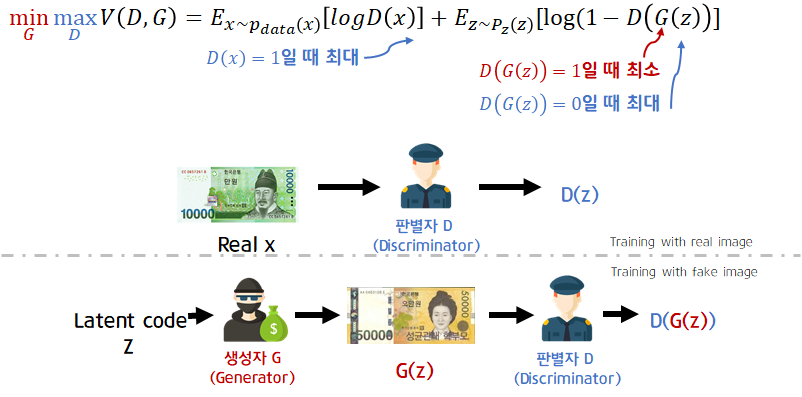
- 판별자 D는 loss를 최대화 하는 것을 목표로합니다.
- 생성자 G는 loss를 최대화 하는 것을 목표로 합니다. 생성자의 입력은 x와 관련 없기 때문에, 항은 고려하지 않습니다.
DCGAN
DCGAN(Deep Convolutional GAN,2015)는 CNN구조로 판별자 D와 생성자 G를 구성한 GAN입니다. 판별자 D는 이미지(예 28x28x3)를 입력으로 받아 binary classification을 수행하므로 CNN구조를, 생성자 G는 random vector z(예 (100,1))를 입력으로 받아 이미지(28x28x3)을 생성해야므로 deconvolutional network구조를 갖게됩니다.
또한 pooling layer를 사용하지 않고 stride 2이상인 convolution,deconvolution을 사용하였습니다.
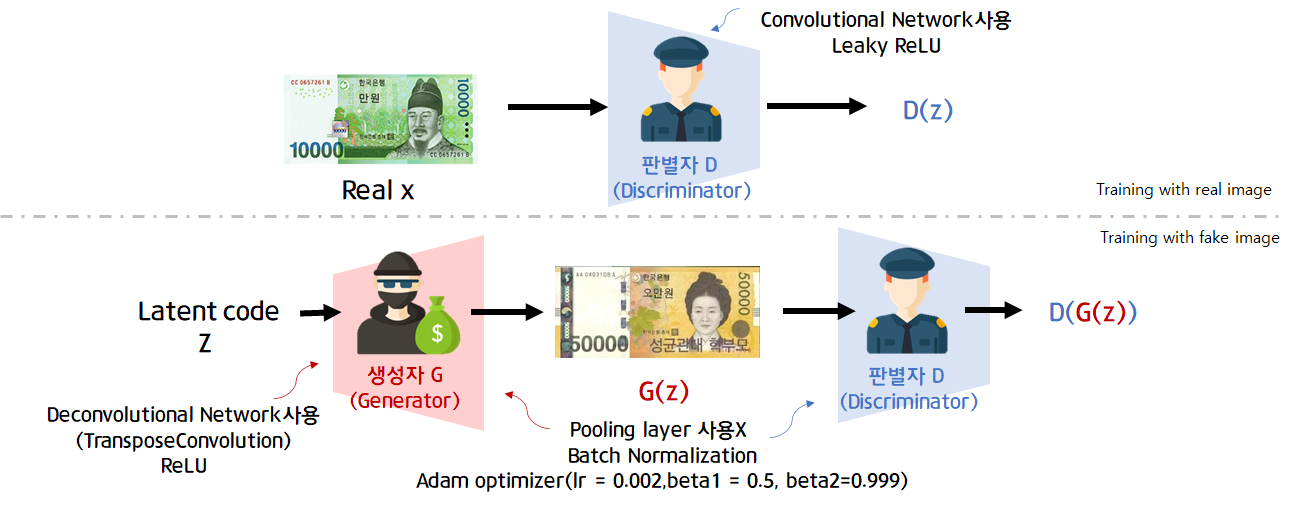
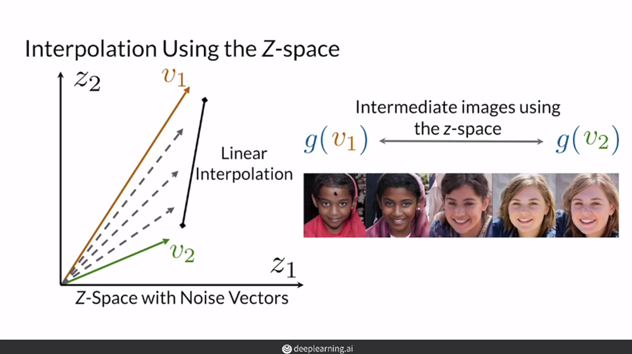
DCGAN의 논문에서, Z space의 연산이 가능하다는 내용을 언급합니다.
예를 들어, "안경 쓴 남자"에 해당하는 z-vector에서 "안경을 쓰지 않은 남자"에 해당하는 z-vector를 빼고, "안경을 쓰지 않은 여자"에 해당하는 z-vector를 더한다면 그 z-vector로 생성한 이미지는 "안경을 쓴 여자"라는 겁니다. (vector space arithmetic)
[하지만, "안경 쓴 남자"-"안경 쓰지 않은 남자"에 해당하는 z-vector로 이미지를 생성한다고 "안경"의 이미지가 나오는 것은 아닙니다. ]
Wasserstein GAN(WGAN)
BCE Loss의 문제점
1. Mode Collapse (모드 붕괴)
Mode collapse는 GAN에 BCE loss를 사용할 때 생기는 문제 중 하나입니다. 생성자가 다양한 이미지를 만들어내지 못하고 비슷한 이미지만 계속해서 생성하는 경우를 뜻합니다. 이는 생성자가 판별자를 속이는 적은 수의 샘플을 찾을 때 일어납니다. 따라서 한정된 이 샘플 이외에는 다른 샘플을 생성하지 못합니다.
즉, 생성자가 local minimum에 빠지게 된것입니다.
mode란? 데이터 분포에서 Mode란, 관측치가 높은 부분을 의미합니다. 정규분포에서는 평균이 분포의 Mode입니다.Mode가 1개이면 single mode 2개인 경우는 bimodal이라고 하고, 2개이상인 경우를 multimodal,mulitple modes라고 합니다.
MNIST dataset의 경우 숫자마다 1개의 mode, 총 10개의 모드가 있는 multiple modes분포로 나타나게 됩니다.
[출처 : deeplearning.ai "Build Basic Generative Adversarial Networks (GANs)" 강의자료]
2. Vanishing Gradient (기울기 소실)
BCE loss는 아래 수식과 같습니다.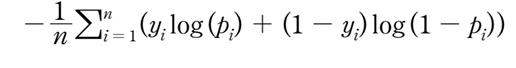
GAN에 적용될 때에는 다음과 같이 나타낼 수 있습니다. 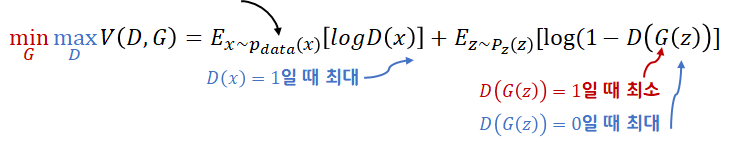 생성자는 BCE를 줄이는 방향으로, 판별자는 BCE를 최대화 하는 방향으로 학습을 진행하고 이를 minimaxgame이라고 합니다. minimaxgame을 하면서 을 와 유사하게 만듭니다.
생성자는 BCE를 줄이는 방향으로, 판별자는 BCE를 최대화 하는 방향으로 학습을 진행하고 이를 minimaxgame이라고 합니다. minimaxgame을 하면서 을 와 유사하게 만듭니다.
이때 판별자와 생성자중에, 생성자를 학습하는 것이 더 어렵습니다. 예를들어, 판별자는 real/fake(1/0)를 구분하면 되지만, 생성자는 28x28x3이미지를 생성해야하기 때문입니다. 즉 판별자 D가 생성자 G보다 학습이 쉽다는 것입니다.
하지만, 학습 초기에는 판별자의 성능이 좋지 않기 때문에 크게 문제가 되지 않습니다.(아래 그래프) 이런 경우에는 0이 아닌 gradient값이 생성자에게 유용한 피드백을 줄 수 있습니다.
 [출처 : deeplearning.ai "Build Basic Generative Adversarial Networks (GANs)" 강의자료]
[출처 : deeplearning.ai "Build Basic Generative Adversarial Networks (GANs)" 강의자료]
그러나 판별자 D의 학습이 잘 될수록 생성되는 분포 와 를 훨씬 더 구별하게 됩니다. 실제 데이터 분포는 에 가까이 위치하고, 생성되는 분포 는 0에 근접하게됩니다. 결과적으로 판별자 D가 잘 학습될수록 0에 가까운 gradient를 넘겨주게 되고, 이는 생성자G입장에서 유익하지 않은 피드백입니다. 결국 생성자는 학습을 종료하게됩니다.
 [출처 : deeplearning.ai "Build Basic Generative Adversarial Networks (GANs)" 강의자료]
[출처 : deeplearning.ai "Build Basic Generative Adversarial Networks (GANs)" 강의자료]
결론적으로 D가 학습중에 잘 개선될 때 cost function의 flat한 영역에 위치하게 되고 이는 와 가 서로 너무 달라서 D가 real과 fake를 너무 잘 구분할 수 있는것을 의미한다. cost funtion의 flat한 영역에 위치하게되어 gradient vanishing문제에 빠진다.
Wasserstein Loss
위에서 말한 GAN에서의 BCE loss의 문제(mode collapse, vanishing gradient)를 개선하기 위해 새로운 loss Wasserstein loss(와서스테인 로스)를 사용합니다. WGAN에서는 새로운 loss를 사용하는 판별자 D를 비평자 C(Critic)라고합니다.(GvsC)
Earth Mover's Distancce
GAN의 목표인 "와 동일하도록 을 학습"은 와 두 분포사이의 거리를 줄이는것으로 생각 할 수 있습니다.
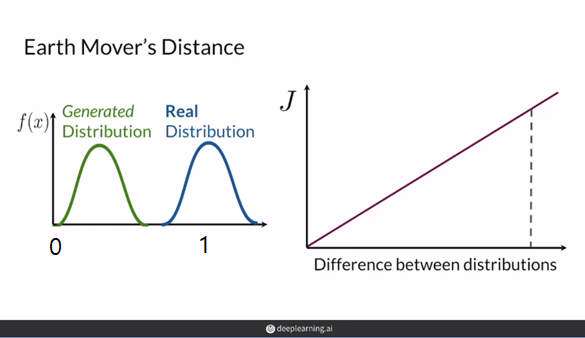
Earth Mover's Distance는 두 분포가 얼마나 다른지를 나타내는 수치입니다. 을 와 동일하게 만들기 위해 이동해야하는 거리와 양을 의미합니다.
BCE loss의 문제는 판별자 D가 sigmoid를 사용하여 real/fake의 확률값을 출력으로하여, 판별자가 좋아짐에 따라 두 분포의 차이가 심해져서 cost funtion의 기울기가 0값인 영역에 위치해 vanishing gradient문제가 생긴다는 것이었습니다. 하지만, Earth Mover's Distance의 결과는 0과 1의 한계가 없습니다. 분포가 얼마나 멀리 떨어져 있든 상관없이 의미있는 gradient(0이 아닌 기울기)를 전달할 수 있습니다. Earth Mover's Distance를 loss에 사용하면 결과적으로 Vanishing Graident해결할 수 있고, Model collapse가능성을 감소시킵니다!
두 확률 분포간의 거리를 나타내는 지표중 왜 Earth Mover's Distance일까?
두 확률 분포간의 거리를 나타내는 지표
1.Total Variation(TV)
2.Kullback-Leibler(KL) Divergence
3.Jensen-Shannon(JS) Divergence
4.Earth Mover's Distance
EM distance(=Wasserstein 거리)의 경우 추정하는 모수에 상관없이 일정한 수식을 가지고 있으나, 다른경우 모수에 따라 거리가 달라질 뿐만 아니라 그 값이 상수 또는 무한대의 값을 가지게됩니다.
TV,KL/JS Divergence는 두 분포가 서로 겹치는 경우에 0, 겹치지 않는 경우에는 무한대 또는 상수로 극단적인 값을 가지게됩니다. 결론적으로 TV,KL/JS Divergence을 loss로 사용한다면 gradient가 제대로 전달되지 않아 학습이 어려워집니다.
더 많은 정보 : Wassertein GAN 수학 이해하기
그럼 Earth Mover's Distance을 사용한 Wasserstein loss를 알아봅시다. Kantorovich-Rubinstein Duality Theorem을 이용하여 Earth Mover's Distance를 다음과 같이 나타낼 수 있습니다. 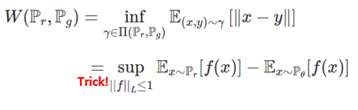
학습시키기 위해 parameter가 추가된 f 로 수식을 바꾸고, Pθ를 g(θ)에 대한 식으로 바꾸면 아래와 같은 수식이 됩니다.
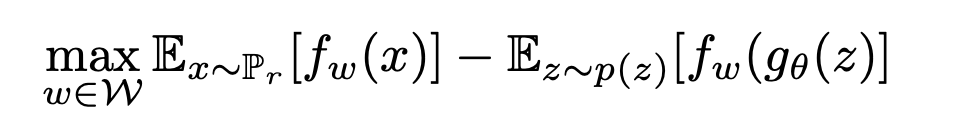
오잉! GAN의 로스와 비슷한 형태군요!를 비평가 C(판별자 D)로 바꾸면!!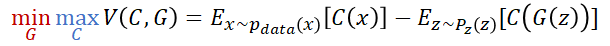 Wasserstein Objective function 완성!
Wasserstein Objective function 완성!
(Wasserstein loss = ,
real x -> fake ->
WGAN조건
Earth Mover's Distance의 출력이 [0, 1]로 제한되지 않아 loss에 사용하는것이 적적하다는 것을 알아보았는데, 일반적으로 신경망에서 너무 큰 숫자는 피해야 하기 때문에 Lipshitz 제약이라는 제약조건을 걸어줍니다.
비평자 C (판별자 D)가 1-Lipshitz continuous function(1-립시츠 연속합수)이어야 합니다. 아래식을 만족하면 됩니다.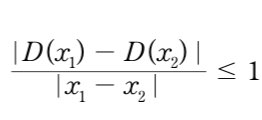 는 비평자C예측 간의 차이의 절댓값이고, 는 두 이미지의 픽셀의 평균값 차이의 절댓값입니다. 1-립시츠 연속함수의 경우 기울기의 절댓값의 최대는 1입니다. 함수 위 어느 점에 원뿔을 놓더라도 하얀색 원뿔에 들어가는 영역이 없습니다. 다른 말로 하면 아래 직선은 어느 지점에서나 상승하거나 하강하는 비율이 한정되어있습니다.
는 비평자C예측 간의 차이의 절댓값이고, 는 두 이미지의 픽셀의 평균값 차이의 절댓값입니다. 1-립시츠 연속함수의 경우 기울기의 절댓값의 최대는 1입니다. 함수 위 어느 점에 원뿔을 놓더라도 하얀색 원뿔에 들어가는 영역이 없습니다. 다른 말로 하면 아래 직선은 어느 지점에서나 상승하거나 하강하는 비율이 한정되어있습니다.
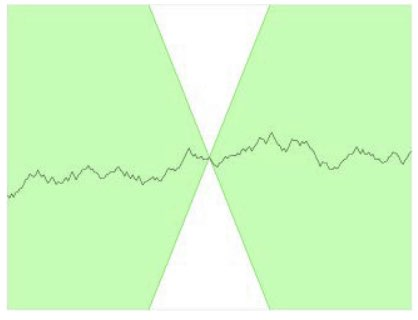
가중치 클리핑 (weight clipping)을 통해 립시츠 제약을 부과할 수 있습니다. WGA 논문에서는 비평자 C의 가중치를 [-0.01, 0.01]안에 놓이도록, 훈련 배치가 끝난 후 가중치 클리핑을 통해 립시츠 제약을 부과하는 방법을 보였습니다. (0.01은 논문에서 실험을 통해 얻은 값입니다.)
WGAN구조
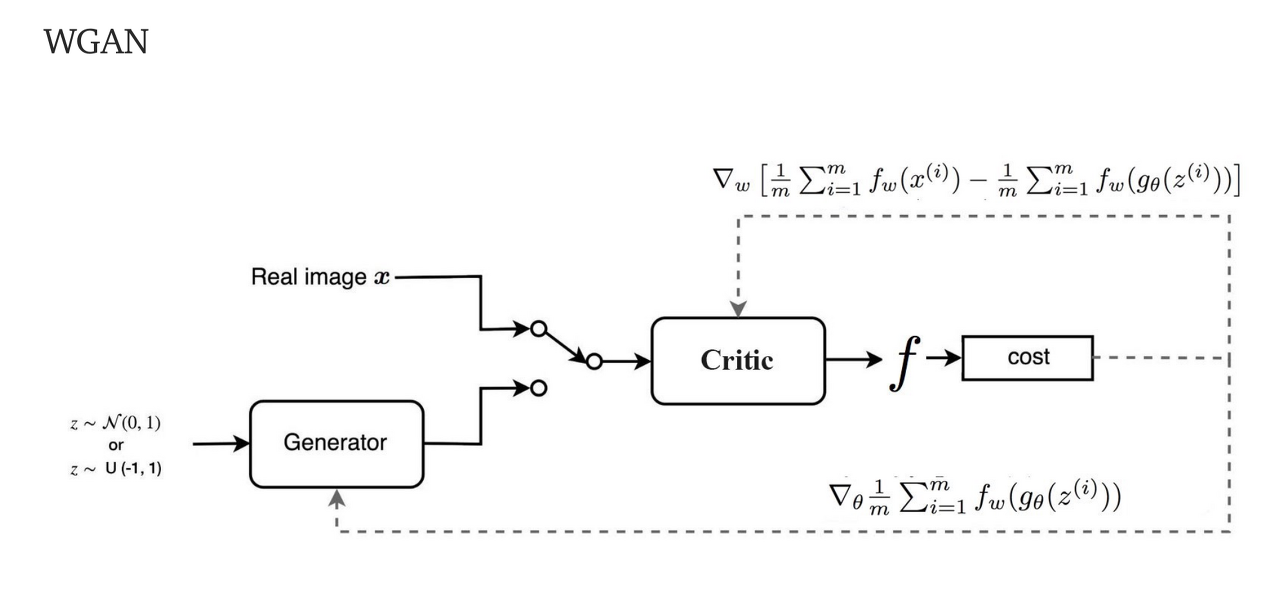
def train_one_step(self,batch_images):
batch_z = np.random.uniform(-1, 1,[self.batch_size, self.z_dim]).astype(np.float32)
real_images = batch_images
with tf.GradientTape() as g_tape, tf.GradientTape() as d_tape:
fake_imgs = self.g(batch_z, training=True)
d_fake_logits= self.d(fake_imgs, training=True)
d_real_logits= self.d(real_images, training=True)
critic_loss=tf.reduce_mean(d_fake_logits-d_real_logits)
g_loss = self.g_loss_fun(d_fake_logits)
gradients_of_d = d_tape.gradient(critic_loss, self.d.trainable_variables)
# for WGAN model all the gradients should clip to (-0.01,0.01)
for idx,grad in enumerate(gradients_of_d) :
gradients_of_d[idx]=tf.clip_by_value(grad,-0.01,0.01)
gradients_of_g = g_tape.gradient(g_loss, self.g.trainable_variables)
self.d_optimizer.apply_gradients(zip(gradients_of_d, self.d.trainable_variables))
self.g_optimizer.apply_gradients(zip(gradients_of_g, self.g.trainable_variables))
self.g_loss_metric(g_loss)
self.critic_loss_metric(critic_loss)
바닐라맛 GAN은?
# train for one batch
@tf.function
def train_one_step(self,batch_images):
batch_z = np.random.uniform(-1, 1,[self.batch_size, self.z_dim]).astype(np.float32)
real_images = batch_images
with tf.GradientTape() as g_tape, tf.GradientTape() as d_tape:
fake_imgs = self.g(batch_z, training=True)
d_fake_logits = self.d(fake_imgs, training=True)
d_real_logits = self.d(real_images, training=True)
d_loss = self.d_loss_fun(d_fake_logits, d_real_logits)
g_loss = self.g_loss_fun(d_fake_logits)
gradients_of_d = d_tape.gradient(d_loss, self.d.trainable_variables)
gradients_of_g = g_tape.gradient(g_loss, self.g.trainable_variables)
self.d_optimizer.apply_gradients(zip(gradients_of_d, self.d.trainable_variables))
self.g_optimizer.apply_gradients(zip(gradients_of_g, self.g.trainable_variables))
self.g_loss_metric(g_loss)
self.d_loss_metric(d_loss)Conditional GAN(CGAN)
Conditional GAN과 Unconditional GAN의 차이는 다음과 같습니다.
| Conditional | Unconditional |
|---|---|
| Exaples from the classes you want | Examples from random classes |
| Training dataset needs to be labeled | Training dataset doesn't need to be labeled |
Conditional GAN(이하CGAN)은 생성자와 판별자가 훈련하는 동안 추가 정보를 사용해 조건이 붙는 생성적 적대 신경망입니다. CGAN을 이용하면 우리가 원하는 class가 담긴 데이터를 생성할 수 있습니다. 생성자와 판별자를 훈련하는 데 모두 label을 사용합니다. 아래 그림은 CGAN의 구조입니다.
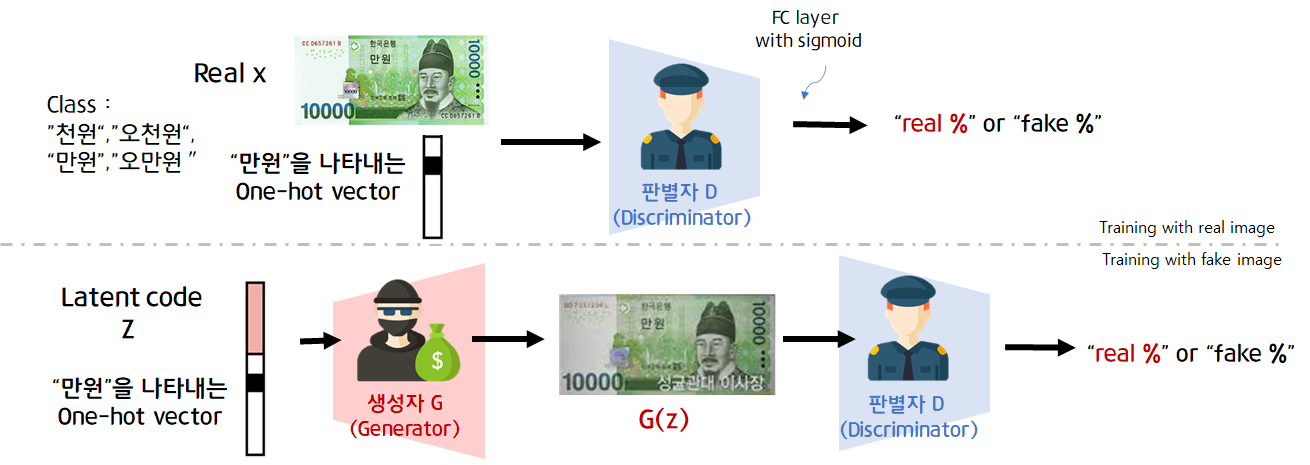
| 생성자 Generator | 판별자 Discriminator | |
|---|---|---|
| 입력 | 랜덤벡터(랜덤노이즈)와 레이블 | train dataset의 (x,y), 생성자가 만든 가짜 sample과 해당 label (G(z,y)),y |
| 출력 | 주어진 label에 가능한 맞도록 생성된 가짜 sample : G(z,y) = x* given y | 입력 sample이 진짜이고 sample-label 쌍이 맞는지 나타내는 하나의 확률 |
| 목표 | label에 맞는 진짜처럼 보이는 가짜sample 생성 | 생성자가 만든 가짜sample-label 쌍과 train dataset의 진짜sample-label 쌍 구별하기 |
판별자의 입력
판별자에는 label(one-hot vector)와 이미지가 입력으로 들어갑니다.

label vector를 embedding layer에 통과시켜 이미지와 동일한 사이즈로 만들고, Concate합니다. 이렇게 one-hot vecotr인 labe과 이미지를 한번에 입력합니다.
생성자의 입력
생성자의 입력으로 들어가는 random noise z는 생성되는 이미지의 다양성이 보장되도록 합니다. 랜덤벡터(랜덤노이즈)와 레이블이 동시에 들어가게됩니다. 단, 그냥 vector concate의 형식 [random vector z,label y]은 아닙니다.
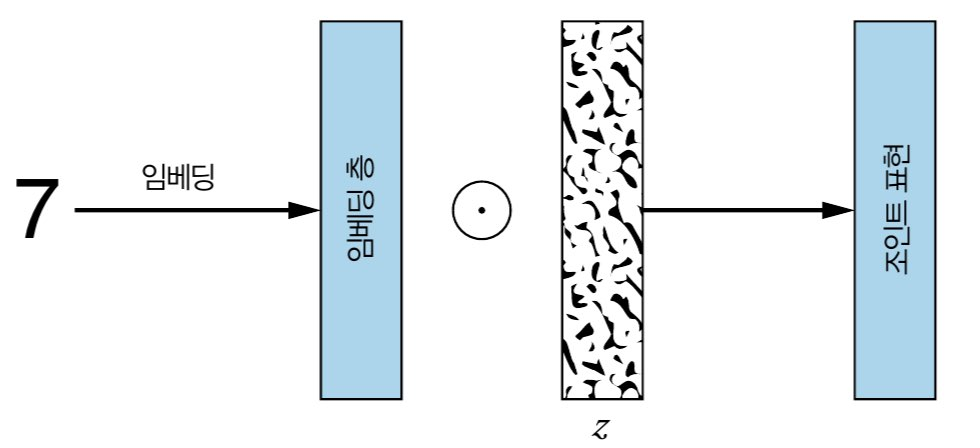
z-dim에 맞게 label vector크기 변환(ex keras embedding층)해서 원소곱(Multiply)해서 들어가게됩니다.
아래는 CGAN말고 seimi-supervised 형식의 GAN의 구조를 표현한 그림입니다.
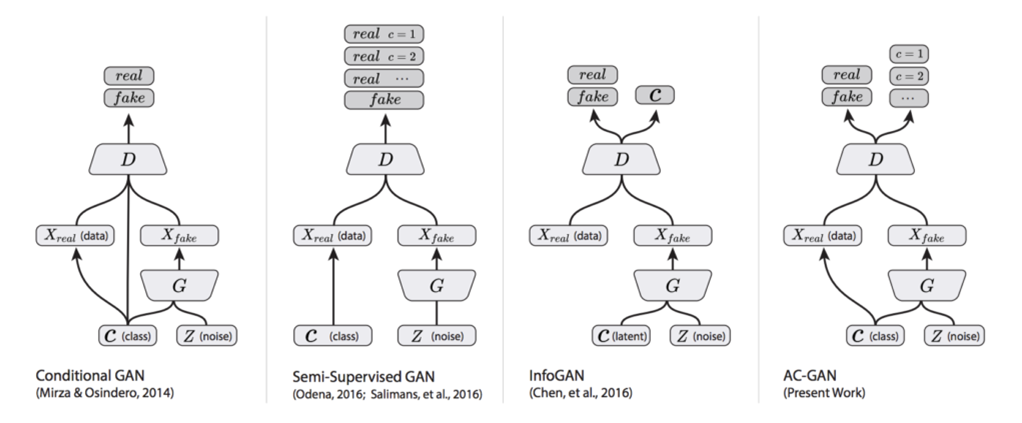
SGAN
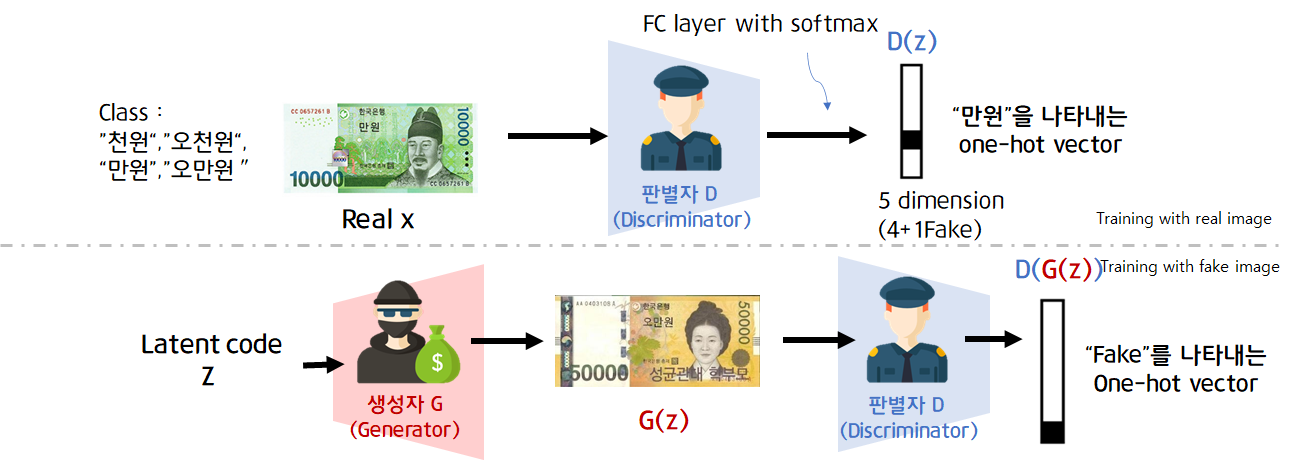
ACGAN
Controllable Generation
학습 중 라벨을 활용하는 CGAN과 달리, 학습 후에 원하는 기능을 조절하도록 할 수도 있습니다.
Controllable은 class를 조절할 수 있는 CGAN과는 다릅니다.
| Controllable | Conditional |
|---|---|
| Example with the features that you want | Exaples from the classes you want |
| Training dataset doesn't need to be labeled | Training dataset needs to be labeled |
| Manipulate at the z-vector input | Append a class vector to the input |
즉, random vector z를 조절하여 feautre를 변화시킬 수 있다는것입니다.
Disentanglement에 관한 자세한 내용은 4주차 이예지님의Disenstanglement를 참고하시기 바랍니다.
[reference]
투빅스 14기 정규세션 10주차 강의자료 : https://drive.google.com/file/d/1syOw-5YZPfHlVAdQJiLnkBXbD39262Kq/view
CS231n 13rkd Generative Model : https://www.youtube.com/watch?v=5WoItGTWV54
미술관에 GAN 딥러닝 실전 프로젝트 - 데이비드 포스터(한빛미디어)
GAN 인 액션 - 야쿠프 란그르,블라디미르 보크(한빛미디어)
Deeplearning.ai "Generative Adversarial Networks (GANs) Specialization" Course1 Basic of GANs : https://www.coursera.org/learn/build-basic-generative-adversarial-networks-gans?utm_source=deeplearningai&utm_medium=institutions&utm_campaign=DLWebGANsMain
WGAN : https://ahjeong.tistory.com/7
10개의 댓글
투빅스 13기 이예지:
이번 강의는 GAN 기초로, 신민정님께서 진행하셨습니다.
-
GAN의 구조
GAN은 genrator와 discriminator로 이루어져 있습니다. 두 뉴럴넷이 서로 겨루며 훈련하기 때문에 "Adversarial" 이라는 단어를 사용합니다. -
Wasserestein GAN
최초 GAN에서 BCE loss를 사용했기 때문에 BCE loss를 사용한 연구가 많았습니다.
그러나 BCE loss는 다음 두 가지의 문제가 있습니다.
(1) Mode Collpase - 생성자가 판별자를 잘 속이기 위해 적은 수의 샘플만을 찾을 때 발생합니다. 이로 인해 다양한 이미지를 생성할 수 없게 됩니다.
(2) Vanishing Gradient - 학습 중 판별자가 성능이 좋아짐에 따라 두 분포의 차이가 심해져서 cost function의 기울기가 0값인 영역에 위치할 수 있습니다.
따라서 이러한 문제점을 해결하기 위해 Wasserestein loss를 사용한 GAN이 등장합니다. -
Conditional GAN
Vanila GAN의 경우 어떤 데이터를 뽑을지 통제하기 힘듭니다.
이를 해결하기 위해 입력값에 클래스 정보와 같은 조건 정보를 추가로 넣어주는 신경망인 CGAN이 등장하게 됩니다.
따라서 생성자의 입력에는 random noise vector 뿐만 아니라 클래스와 같은 레이블이 들어가게 됩니다. -
Controllable Generation
GAN이 모델을 생성할 때 얼마나 생성이미지를 왜곡시킬지 조절할 수 있는 모델입니다.
GAN의 전반적인 설명과 설명과 흐름에 대해 설명해주어서 좋았습니다.
특히 컨퍼런스에 도움되는 모델들이 많아서 더더욱 유익했습니다.
좋은 강의 감사합니다 :)
투빅스 14기 김상현
이번 강의는 GAN 기초로 투빅스 13기 신민정님께서 진행하셨습니다.
GAN의 기초 원리와 GAN의 문제를 해결하기 위한 WGAN을 설명해주셨습니다. 또한 원하는 결과를 얻기 위한 conditional GAN과 controllable Generation이 인상 깊었습니다.
- 생성모델링은 sample x의 P(x)를 추정하는 것입니다. 생성 모델의 한 종류인 GAN은 Generative Adversarial Network의 약자로 G(생성자)와 D(판별자)가 서로 적대적으로 학습하면서 훈련하는 모델입니다.
- Real/fake를 구분하면서 학습을 진행하기 위해 이진크로스엔트로피 BCE를 손실함수로 하여 학습을 진행하는데, 이때 mode collapse와 vanishing gradient 문제가 발생합니다. 이를 극복하기 위해 Wasserstein loss를 사용한 WGAN이 제안되었습니다.
- WGAN은 두 분포의 차이를 나타내는 Earth Mover’s Distance를 loss에 사용해 Wasserstein loss를 이용합니다. Earth Mover’s Distance의 출력이 [0,1]에 제한되지 않아 loss에 사용이 적합하지만, 신경망에서 너무 큰 숫자를 피하기 위해 Lipshitz제약을 사용하여 기울기의 절대값의 최대를 1로 합니다. 해당 제약은 가중치 클리핑을 이용하여 부과합니다.
- 기존의 GAN은 원하는 class의 결과를 얻으려면 무작위성에 기대했습니다. 반면에 Conditional GAN은 Label을 나타내는 one-hot vector를 추가로 입력해줘서 원하는 class 생성 결과를 얻을 수 있습니다. 판별자의 경우 label vector를 embedding한 후 이미지와 concat하여 입력한다. 생성자의 경우 label vector를 embedding한 후 random noise와 element-wise 곱한 결과를 입력합니다.
- Controllable Generation은 학습 후 원하는 기능을 조절하는 것으로 random vecor z를 조절하여 feature을 변화시킬 수 있습니다. Class를 조절하는 Conditional GAN과는 차이가 있습니다.
GAN의 기초원리와 발전된 모델들을 배울 수 있었습니다. 좋은 강의 감사합니다!
투빅스 12기 김태한
- 생성모델에 해당하는 GAN에 대하여 기초를 쌓을 수 있는 강의였습니다. 새로운 데이터를 생성하고자 하는 G와 이를 실제 데이터와 구분하고자하는 D간의 서로 적대적인 학습과정으로 이루어지며 일반적으로 latent vector z를 gaussian distribution으로 두었을 때, 해당 분포내에 데이터의 feature분포가 고정되어 정해지는 것이 아닌 D에 의해 임의의 분포가 찾아지는 형태의 구조로 되어있습니다.
- 이러한 GAN은 다양한 형태가 존재하며 DCGAN, WGAN, Controllable Generation이 그 대표적인 예 입니다. 이는 이러한 GAN의 학습시 G와 D가 학습하는데 있어 D가 너무 학습이 잘 되어버리면 G의 학습방향을 높이는 gradient가 생성되지 않는 문제가 발생하게 됩니다. 이러한 점을 해결하기 위하여 기존의 BCE Loss를 Wasserstain loss로 바꾸어 해결하려는 시도가 WGAN이며, 이미지같은 복잡한 feature에 대하여 cnn기법을 적용한 DCGAN, 마지막으로 GAN학습 이후 latent vector z를 이용하여 feature를 변화시키는 방법인 controllable generation이 해당됩니다.
GAN의 기초원리 및 기초 변화과정에 대하여 알 수 있는 좋은 기회였습니다. 감사합니다.
투빅스 14기 정재윤
이번 강의는 GAN 기초로, 신민정님께서 강의를 진행해주셨습니다.
- 기본적인 GAN의 구조를 설명하고 그 때의 loss에 대해서 설명해주셨습니다. 주로 GAN의 loss는 BCE loss를 사용하는데요. 이 BCE loss는 큰 문제점 2가지를 야기합니다. 첫째로 mode collapse입니다. 판별자가 너무 하나의 이미지를 정확하게 구분해낸다면 생성자가 이를 바탕으로 학습을 진행해, 다양한 output을 도출하지 못하게 됩니다. 이 같은 현상을 mode collapse라고 합니다. 이런 현상을 막기 위해선 판별자와 생성자의 learning rate를 다르게 두어 판별자가 더 천천히 학습할 수 있게 만들어줘야 한다고 합니다. 두번째로 vanishing gradient입니다. 이 역시 판별자의 학습 속도가 너무 빠르기 때문에 발생한다고 합니다. 판별자가 학습을 빠르게 진행하고 잘 될수록, loss가 제대로 갱신되지 않아서 생성자가 역전파를 받을 때 유의미한 학습을 할 수 없게 된다고 합니다.
- 이 같은 문제를 개선하기 위해 만들어진 loss function이 Wasserstein loss 입니다. 이 loss는 기존에 사용하던 거리가 아닌 Earth Mover’s distance를 사용하는데요. 간단하게 두 분포를 동일하게 만들기 위해서 이동해야하는 거리와 양을 의미합니다. 기존의 loss와 확연하게 차이가 나는 것은 이 distance의 결과는 0과 1 사이의 값이 나오는 것이 아닌 실수 전체 범위라는 것입니다. 그러다보니 상대적으로 BCE loss를 사용할 때 나오는 문제들을 더 잘 해결할 수 있습니다.
- Conditional GAN과 Controllable GAN 역시 인상깊었습니다. Conditional GAN은 모델에 input에 class vector를 넣음으로써 자신이 원하는 조건에 맞춰 이미지를 생성하는 생성모델입니다. 반면 controllable GAN은 conditional GAN과는 다르게 학습 후에 원하는 기능을 조절하는 생성모델입니다. 즉, 학습 전과 학습 후라는 큰 차이를 가지고 있는 모델들입니다.
앞으로의 세미나들에 있어서 가장 기초가 될 수 있는 생성모델들을 간결하면서도 자세히 설명해주셔서 이해하기 쉬웠습니다. 감사합니다.
투빅스 11기 이도연
GAN의 기초 강의로, 기본 GAN 부터 DCGAN, WGAN, CGAN 까지 다양한 발전된 모델에 대해 공부할 수 있는 강의였습니다. 좋은 강의 감사합니다!
- GAN은 생성자(Generator)와 판별자(Discriminator)의 적대적인 학습을 통해 데이터를 생성하는 모델이다. Generator는 진짜와 같은 가짜 데이터를 생성하는 것이 목적이고, Discriminator는 Generator가 만든 데이터가 진짜인지 가짜인지 잘 구분하는 것이 목적이다. GAN의 Loss는 BCE(Binary Cross Entropy)를 사용한다.
- DCGAN은 이름에서 알 수 있듯이 CNN구조로 성생자와 판별자를 구성한 GAN이다. 해당 논문에서 latent vector z의 interpolation과 연산이 가능하다는 시각화 결과를 보여준 점이 흥미로웠다.
- BCE Loss는 Mode Collapse, Vanishing Gradient의 문제점이 있다. Mode Collapse란 Generator가 다양한 이미지를 만들어 내지 못하고 local minima에 빠지게 된 것이다. 그리고 판별자가 생성자보다 학습이 쉽다는 점에서 판별자의 성능이 좋아짐에 따라 loss function의 gradient가 0에 가까워지며 vanishing gradient 문제가 생긴다. 이러한 문제를 해결하기 위해 loss function을 Wasserstain loss로 재정의 한다.
- Wasserstein loss는 확률 분포 간의 거리를 측정하는 척도 중 하나인 Earth Mover's Distance를 이용하는데 다른 거리 측정 척도(KL, JS divergence)등과 비교했을 때 두 분포가 겹치는 경우에는 0, 겹치지 않는 경우에는 무한대 또는 상수로 극단적인 거리값을 나타내는 것과 달리 일정한 수식을 가지고 있어 문제를 개선할 수 있다.
- WGAN에서는 D 대신 비평자 C를 사용한다. 이 때 EM distance를 사용하기 위한 제약 조건으로 C가 1- Lipschitz 연속함수여야 하는데 이를 위해 weight clipping을 사용한다.
- CGAN은 Conditional GAN으로 추가 조건 y(label 등)를 통해 우리가 원하는 데이터를 생성할 수 있다.
- 마지막으로 Controllable Generation은 모델이 학습된 이후 출력에서 원하는 특징을 조절하는 것으로 noise vector z에서 원하는 방향을 찾아 움직여야 한다. 하지만 z 공간의 얽혀있음으로 인해 원하는 특징 이외에 관계없는 여러 다른 특징들을 변화시키는 등의 어려움이 있어 제어하기가 어렵다.
투빅스 14기 박지은
- GAN은 생성자와 판별자가 서로 경쟁하며 기존의 데이터로부터 새로운 이미지를 생성해 내는 것을 말합니다. 진위 여부 2가지로 나누는 BCE를 사용하여 손실을 계산합니다.
- DCGAN은 CNN 구조로 판별자와 생성자를 구성한 GAN으로, z space의 연산이 가능하다는 특징이 있습니다.
- Wasserstein GAN은 BCE로 손실을 계산할 때의 문제점인 모델 붕괴와 vanishing gradient를 해결하게 해줍니다. Wasserstein loss를 계산할 때, 결과가 0과 1에 한정되어 있지 않은 Earth Mover's Distance를 이용하여 판별자 대신 비평자 C를 둡니다. 이때, 비평자가 1-Lipshitz continuous function이어야 한다는 Lipshitz 제약을 걸어야하는데, 이는 가중치 클리핑으로 부과할 수 있습니다.
- Conditional GAN은 생성자와 판별자가 훈련하는 동안 추가 정보를 사용하여 조건이 붙는 생성적 적대 신경망으로, label을 이미지와 함께 입력하여 원하는 class가 담긴 데이터를 생성할 수 있습니다.
- Controllable Generation은 학습 후에 random vector z를 조절하여 원하는 기능을 조작할 수 있다는 점에서 Conditional GAN과 비교됩니다.
다양한 GAN의 종류를 다룸에도 불구하고, 서로 차이점이 무엇인지 명확하게 잘 설명해주셔서 이해하는 데에 도움이 되었습니다. 감사합니다!
투빅스 14기 박준영
이번 강의는 Gan의 기초로 신민정님께서 강의를 해주셨습니다.
-
생성모델링의 목적은 실제 데이터 분포와 비슷한 생성 모델의 분포를 만드는 것이다.
-
Gan의 구조에서 generator의 input은 랜덤한 숫자로 구성된 벡터Z이고
output은 최대한 진짜 같이 보이는 가짜샘플 G(z)이다.
Discriminator의 input은 훈련 데이터 셋에 있는 실제 샘플 x/ 생성자가 만든 가짜 샘플 z 이고 output은 입력 샘플이 진짜일 예측 확률이다.
이렇게 생성된 generator를 D(G(z))가 1에 가까운 값을 만들어야한다. -
Gan loss는 real or fake를 구분하는 binary cross entropy를 사용한다.
-
DCGAN은 CNN구조로 Discriminator와 generator를 구성한 Gan이다.
Discriminator는 이미지를 입력으로 받아 binary classification을 수행하기에 CNN구조를 가진다.
DCGAN의 Generator는 random vector z를 입력받아 이미지를 생성해야하므로 deconvolution network를 가지게 된다. -
DCGAN은 Z space의 연산이 가능한것이 특징이며 z-vector와 z-vector끼리 더해서 나온 z-vector로 생성한 이미지는
두개의 특징을 합친 이미지가 나온다. (vector space arithmetic) -
WGAN
Gan의 mode collapse, vanishing gradient 문제를 개선하기 위해 새로운 Wasserstein loss를 사용했다.
Wasserstein loss는 Earth Mover's Distance를 사용하여 출력값을0,1으로 제한하지 않았다. 하지만 신경망에 너무 큰 숫자의 출력은 피해야하기때문에 Lipshiz 제약조건을 걸어 기울기의 절대값의 최대를 1로 Wasserstein loss에 제한을 걸었다. -
CGAN
Conditional Gan은 Generator와 Discriminator가 훈련하는 동안 추가 정보를 사용해 조건을 붙여 class가 담긴 데이터를 생성하는 생성모델이다.
CGAN과 다른 Gan과의 차이점은 Discriminator와 Generator를 훈련할 때 one-hot vector된 label을 사용한다는 점이다. -
Controllable Generation
CGAN은 학습중에 label을 활용해서 이미지를 생성했다면 Controllable Generation은 random vector z를 조절하여 feature를 변화 시키는것이 특징이다.
이 강의를 통해 Gan의 구조와 다양한 GAN의 모델을 배워 갈 수 있었습니다. 강의 감사합니다.
투빅스 14기 김민경
- 생성 모델링은 가지고 있는 데이터 분포에서 sampling한 것 같은 새로운 데이터를 만드는 것, 즉 그럴듯한 가짜 데이터를 만들어내는 것이다.
- GAN은 뉴럴 네트워크로 이루어진 Generator, Discriminator가 서로 적대적으로 경쟁하며 훈련한다.
GAN의 Generator는 랜덤 벡터 z를 입력으로 받아 최대한 진짜 같이 보이는 가짜 샘플 G(z)를 출력한다. 보통 z는 균등 분포, 정규 분포같은 단순 분포로 가정한 분포에서 추출한 벡터이다. - GAN의 Discriminator는 훈련 데이터셋에 있는 실제 샘플 x와 생성자가 만든 가짜 샘플 z를 입력으로 받아 입력 샘플이 진짜일 예측 확률을 0에서 1사이 값으로 출력한다.
- GAN의 Discriminator는 바이너리 크로스 엔트로피(BCE) 손실함수를 사용해서 출력값인 예측 확률을 얼마나 잘 맞췄나 측정한다.
- GAN의 한계점으로는 Generator가 다양한 이미지를 만들어내지 못하고 비슷한 이미지만 계속해서 생성하는 상황인 "모드 붕괴", 반대로 Discriminator가 너무 학습을 잘해서 진짜와 가짜를 100% 구분해내는 경우인 "기울기 소실"이 있다.
- DCGAN은 기존의 GAN보다 훨씬 안정적인 학습을 한다는 장점을 갖고 있으며 Discriminator에는 CNN구조를, Generator에는 deconvolutional network구조를 사용했다는 특징이 있다. 또한, pooling layer를 사용하지 않고 모델의 깊은 layer에서는 선형 layer를 사용하지 않았다. 주목할 점은 잠재공간에 실제 데이터의 특성이 투영됐는지 살펴봄으로써 모델이 잘 학습됐는지 알 수 있으며 그 잠재 공간의 연산도 가능하다는 것이다.
- CGAN은 Generator와 Discriminator가 훈련하는 동안 추가 정보를 사용해 조건이 붙는 GAN인데, 이미 있는 이미지를 다른 영역의 이미지를 변형하고 싶은 경우 유용한 모델이다.
- GAN의 기본적인 구조, 다양한 GAN들을 자세히 알 수 있어 정말 좋은 강의였습니다. 감사합니다:)
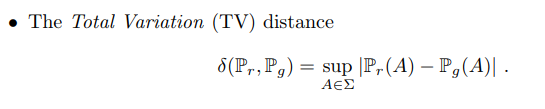
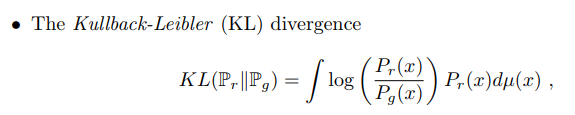
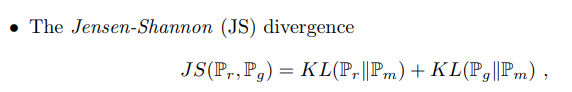






투빅스 14기 한유진
제일 잘알려져있는 GAN은 판별자 D와 생성자 G가 서로 적대적인 관계를 형성하며 새로운 데이터를 생성하는 것입니다. GAN에서는 BCE를 사용하여 모델을 훈련시키지만 모드붕괴, 기울기 소실의 문제를 가지고 있습니다. 그렇기 때문에 Wasserstein Loss를 사용하는 WGAN이 나왔습니다. Wasserstein Loss에서는 Earth Mover’s Distance(두 분포가 얼마나 다른지 나타내는 수치)를 사용하기 때문에 0이 아닌 기울기 값을 넘겨주어 BCE를 사용했을때의 문제점을 보완할 수 있습니다. 식을 살펴보면 BCE와 유사한 형태를 보이지만 Wasserstein Loss에는 Lipshitz제약을 걸어주어야 합니다. 이 제약은 가중치 클리핑을 통해서 코드로 구현할 수 있다고합니다.