GAN 심화 : WGAN(Wasserstein GAN) & CGAN(Conditional Generative Adversarial Nets)
본 게시글에 첨부한 슬라이드는 아래 두 자료에서 발췌하였습니다.
- 임성빈님의 'Wasserstein GAN 수학 이해하기 I',
- 전현규님의 '십분딥러닝_16_WGAN (Wasserstein GANs)'
1. WGAN (Wasserstein GAN)
Introduction
Unsupervised Learning의 MLE 문제 :
↔ Minimizing
MLE 문제를 해결하기 위해서는 KL Divergence가 0으로 수렴해야 하는데, 만약 두 분포의 support가 겹치지 않는다면 KL Divergence는 발산하게 됩니다(=KL Distance가 정의되지 않음).
Noise term을 추가해 두 분포의 support를 겹치게 할 수는 있지만, 샘플의 질을 떨어뜨릴 뿐만 아니라 흐릿한 이미지를 생성하게 됩니다.
따라서, 의 분포를 직접 추정하기보다는 를 결정하는 잠재벡터 의 분포를 가정한 후 입력으로 받아서 Generator를 학습시키는 접근 방식을 선택할 수 있는데, 이러한 방식을 쓰는 것이 GAN(Generative Adversarial Network)입니다.
GAN의 이론적 배경은 탄탄하지만, Discriminator와 Generator 간 학습의 불균형으로 인한 Mode Collapse 문제가 내재합니다.
WGAN은 metric을 변경(cost function을 변경)하여, 기존 GAN의 문제점을 해결하고자 했습니다.
Mode Collapse
: 우리가 학습시키려는 모형이 실제 데이터의 분포를 모두 커버하지 못하고 다양성을 잃어버리는 현상(Generator가 전체 데이터 분포를 찾지 못하고, 하나의 mode에 몰리게 됨).
Discriminator와 Generator 간 학습의 불균형으로 인해 발생합니다.
출처 : https://ratsgo.github.io/generative%20model/2017/12/20/gan/
Different Distances
지금부터는 확률분포 학습에 쓰이는 다양한 metric을 비교하고,
WGAN의 metric인 Earth-Mover(EM) Distance(=Wasserstein-1)을 소개합니다.
Notation
- (Supremum) : 상한(upper bound)에서 가장 작은 값(minimum)
- (Infimum) : 하한(lower bound)에서 가장 큰 값(maximum)
- 참고 : 과 은 항상 존재합니다.
(반면, , 는 항상 존재하는 것은 아닙니다.)
Total Variation (TV)
: 두 확률측도(Probability measure, 확률분포와 동일한 의미로 받아들여도 무방)의 측정값이 벌어질 수 있는 값 중 가장 큰 값(또는 supremum).
만약 두 확률분포의 확률밀도함수가 서로 겹치지 않는다면 TV는 1입니다.
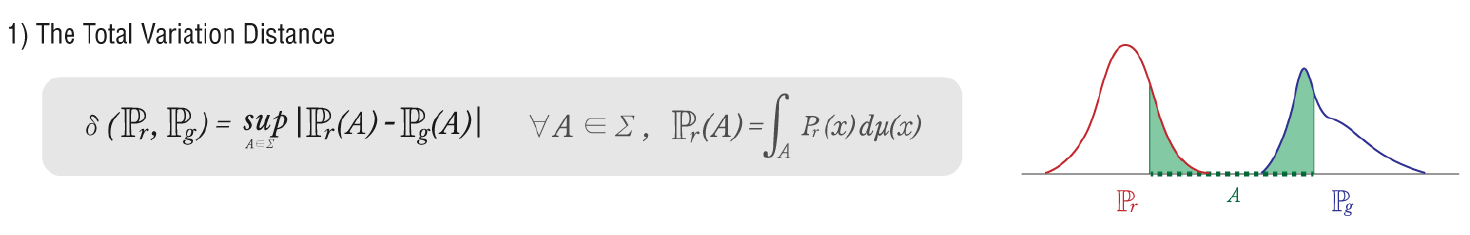
Kullback-Leibler(KL) Divergence & Jensen-Shannon(JS) Divergence

JS-Divergence의 Vanishing Gradient
KL-Divergence와 JS-Divergence를 아래와 같은 수식으로 나타내겠습니다.KL-Divergence :
JS-Divergence :
( : 실제 Data Distribution, : Generator에서 나온 임의의 Distribution)
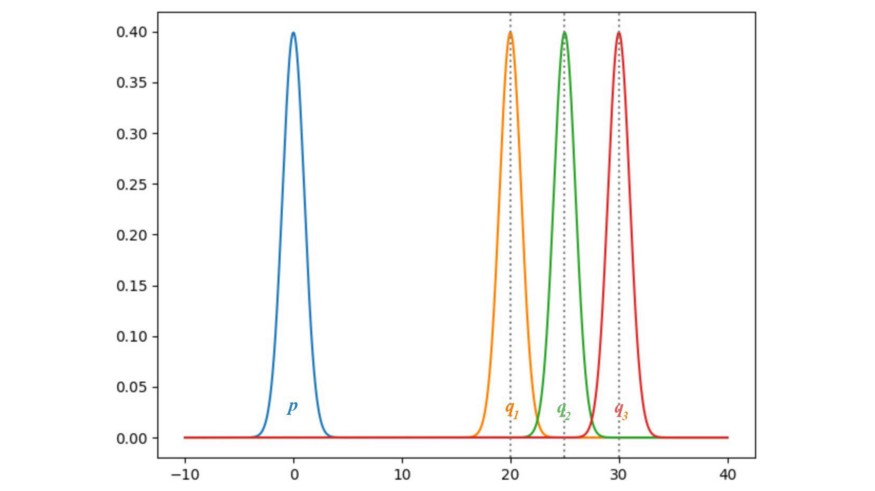
위 확률분포들을 가우시안(Gaussian) 분포로 가정하고, 평균을 0부터 35까지로 제한한 후 와 몇 개의 를 시각화해보면 아래와 같습니다.
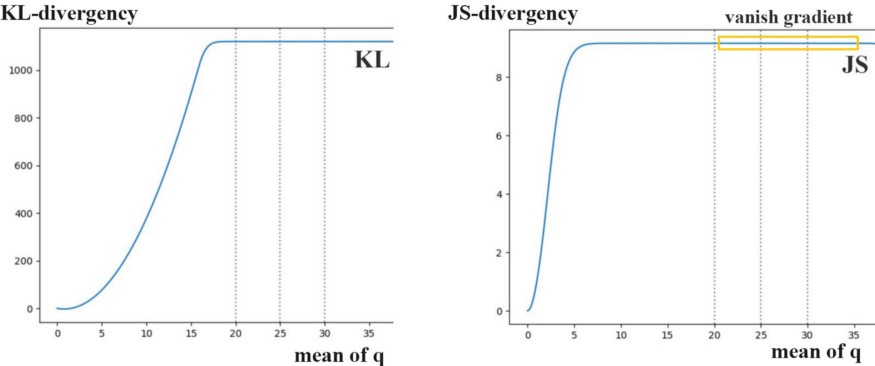
만약 와 가 동일하다면, KL-Divergence와 JS-Divergence는 모두 0이 됩니다. 하지만 의 평균이 점차 커질수록, 두 경우 모두 Divergency의 gradient가 0에 가까워집니다. 이 경우, Generator가 gradient descent 방식으로 학습을 진행해도 진전이 없게 됩니다.
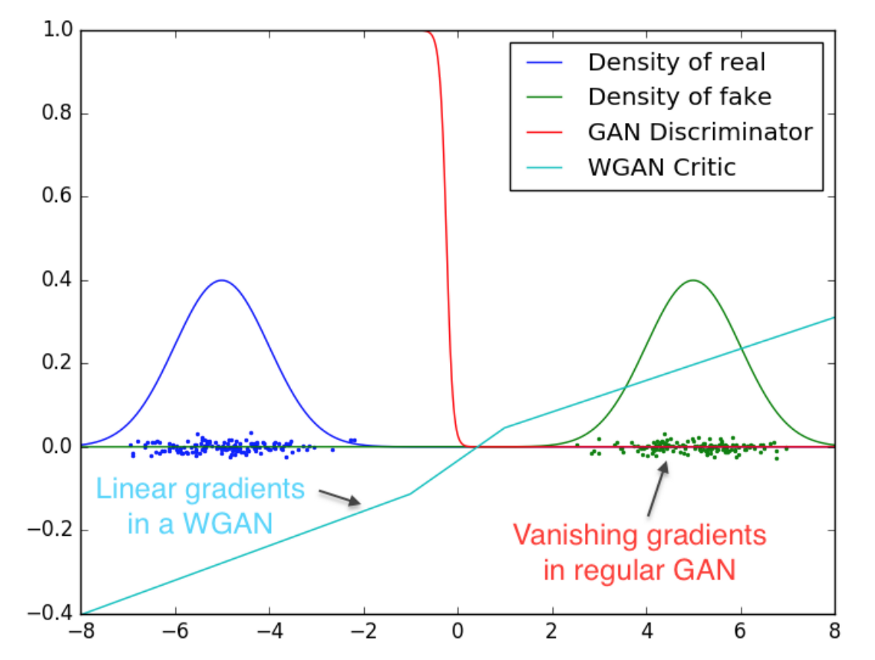
WGAN은 Vanishing Gradient 문제 해결을 위해 Wasserstein Distance에 기반한 새로운 cost function을 도입합니다. 아래는 그 비교 결과입니다.
출처 : https://jonathan-hui.medium.com/gan-wasserstein-gan-wgan-gp-6a1a2aa1b490
Earth-Mover(EM) Distance (=Wasserstein-1)
: 두 확률분포의 모든 결합확률분포(joint distribution) 중에서 의 기댓값을 가장 작게 추정한 값
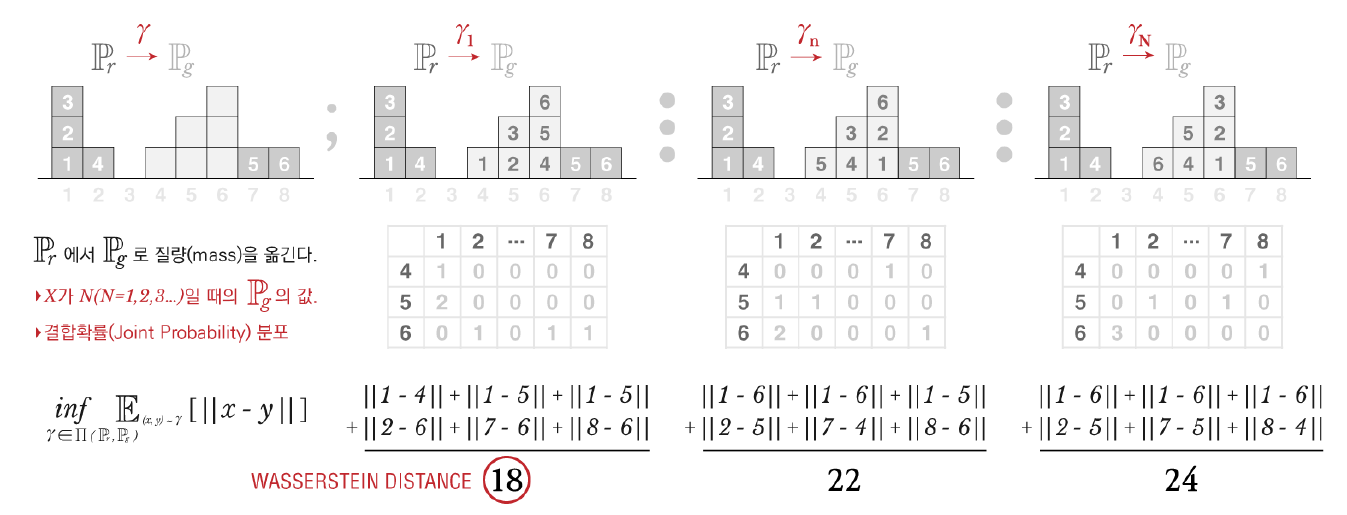
Metric 비교 Example
논문의 예시(Example 1)를 통해 metric의 차이를 더욱 직관적으로 이해하고, Wasserstein Distance의 타당성을 확인할 수 있습니다.
는 좌표는 0, 좌표는 0~1 사이의 값을 가지는 점들의 분포이고,
는 좌표는 , 좌표는 0~1 사이의 값을 가지는 점들의 분포입니다.
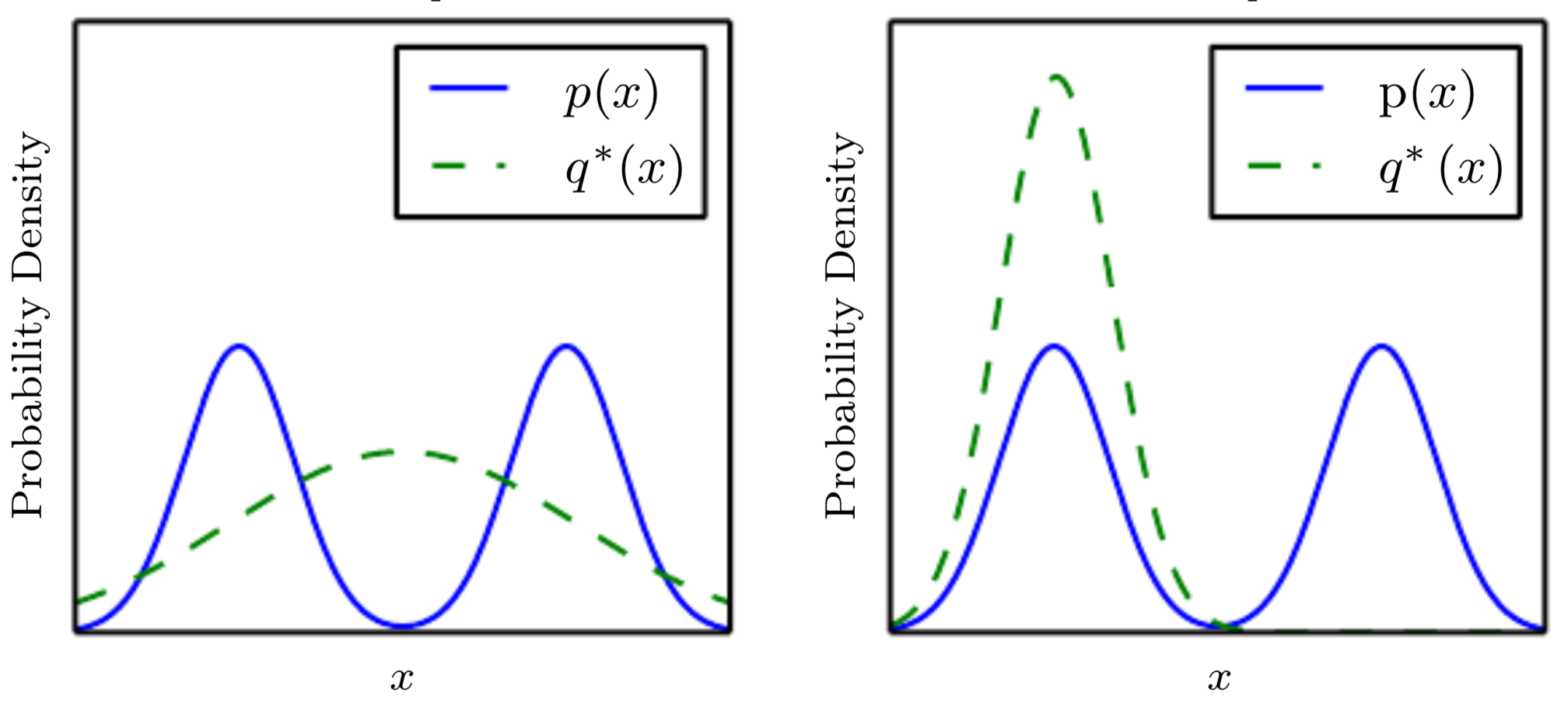
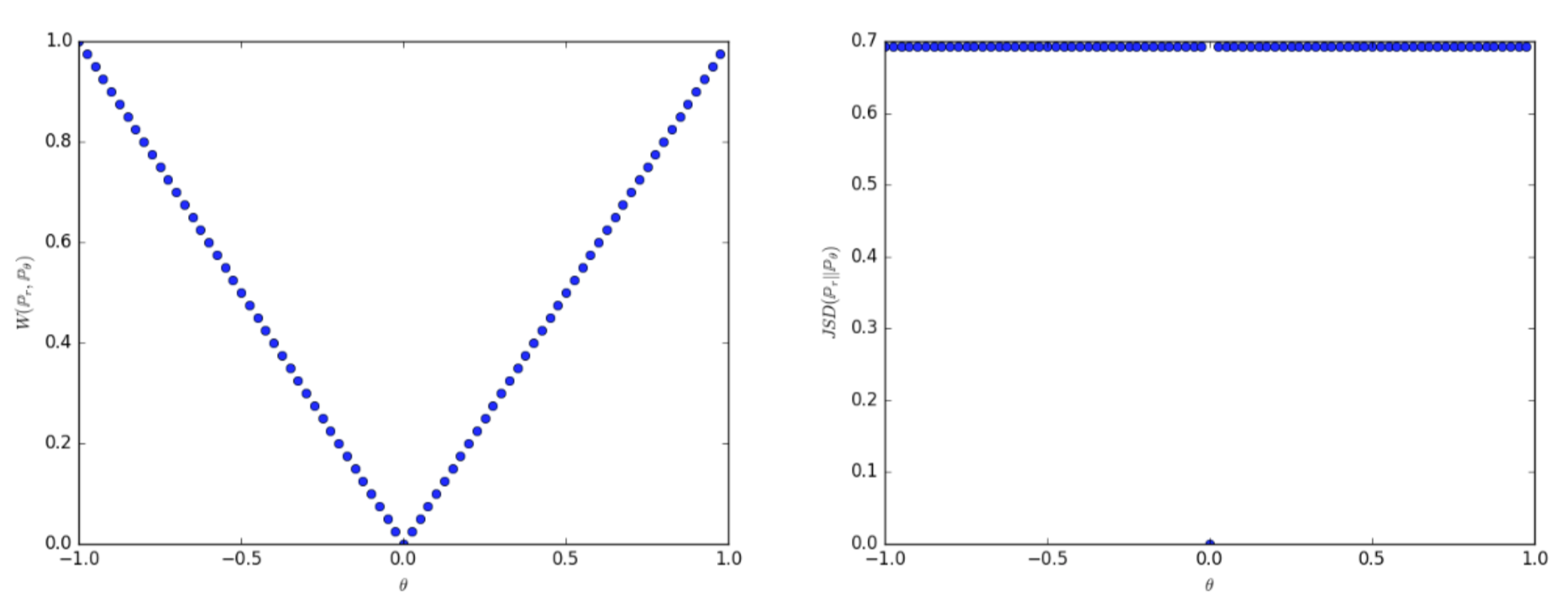
위와 같이 확률분포가 주어진 상황에서, JS Divergence는 가 0일 때만 0이고, 0이 아닌 모든 지점에서는 라는 일정한 값을 갖습니다(오른쪽 그래프). 반면, Wasserstein Distance는 형태로, 두 확률분포 간 차이를 더욱 세밀하게 파악할 수 있습니다(왼쪽 그래프).
위에서 소개한 다른 metric의 결과들은 아래와 같습니다.
TV, KL Divergence, 그리고 JS Divergence의 경우
두 확률분포가 서로 겹치는 경우에는 0, 겹치지 않는 경우에는 무한대() 또는 상수(constant)로 극단적인 거리 값을 보입니다.
참고 : https://ratsgo.github.io/generative%20model/2017/12/21/gans/
왜 'Earth-Mover Distance'일까?
: 과 사이의 Wasserstein Distance는 을 로 옮길 때 필요한 양과 거리의 곱을 가리킵니다. 산등성이 전체를 옮기는 것 같다고 하여 Earth-Mover Distance라고도 불립니다.
출처 : https://ratsgo.github.io/generative%20model/2017/12/21/gans/
Wasserstein GAN
위에서 Wasserstein Distance의 상대적 유용성을 확인했습니다만,
수식의 계산의 어렵습니다(intractable). 를 구하기 위해서는 과 간 결합확률분포를 계산해야 하는데, 은 실제 데이터의 확률분포이기 때문입니다.
이때, Kantorovich-Rubinstein Duality Theorem을 활용하면,
Wasserstein Distance 수식을 아래처럼 새롭게 정의할 수 있습니다.
- Wasserstein Distance :
- Kantorovich-Rubinstein Duality Theorem 활용 :
- : 는 함수(임의의 두 점 간 평균변화율이 1을 넘지 않는 함수)
Kantorovich-Rubinstein Duality Theorem 설명 : https://vincentherrmann.github.io/blog/wasserstein/
위에서 정의된 수식을 새로운 변수 를 도입하여 아래와 같은 수식으로 변경할 수 있습니다. 즉, 새로운 변수 를 추가해 를 업데이트해나가는 방식입니다.
- (GAN Loss와 비슷한 형태)
- : 가능한 의 집합. 로 제한됨 = Weight Clipping
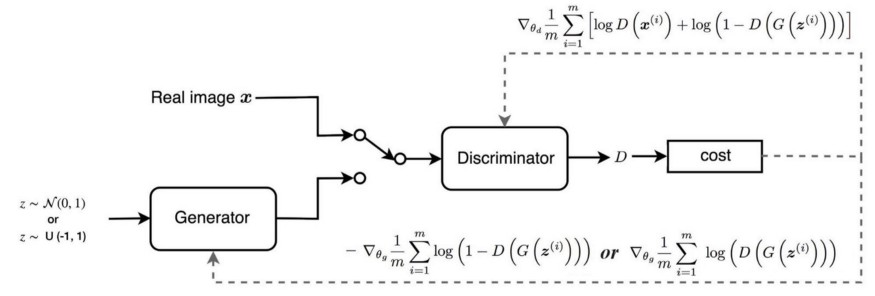
GAN VS WGAN
- GAN 구조
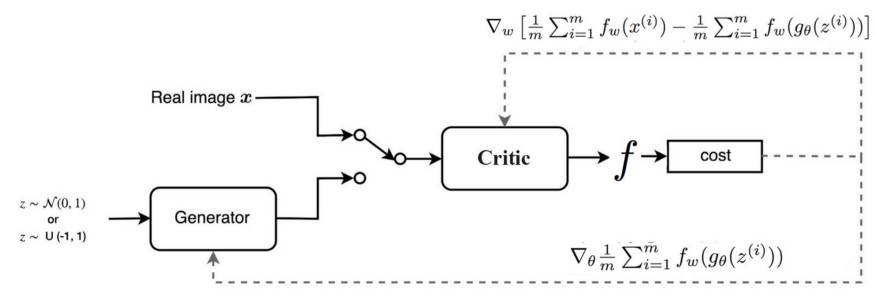
- WGAN 구조
출처 : https://jonathan-hui.medium.com/gan-wasserstein-gan-wgan-gp-6a1a2aa1b490
Empirical Results
전반적인 실험 결과와 성능을 제시합니다.
Experimental Procedure
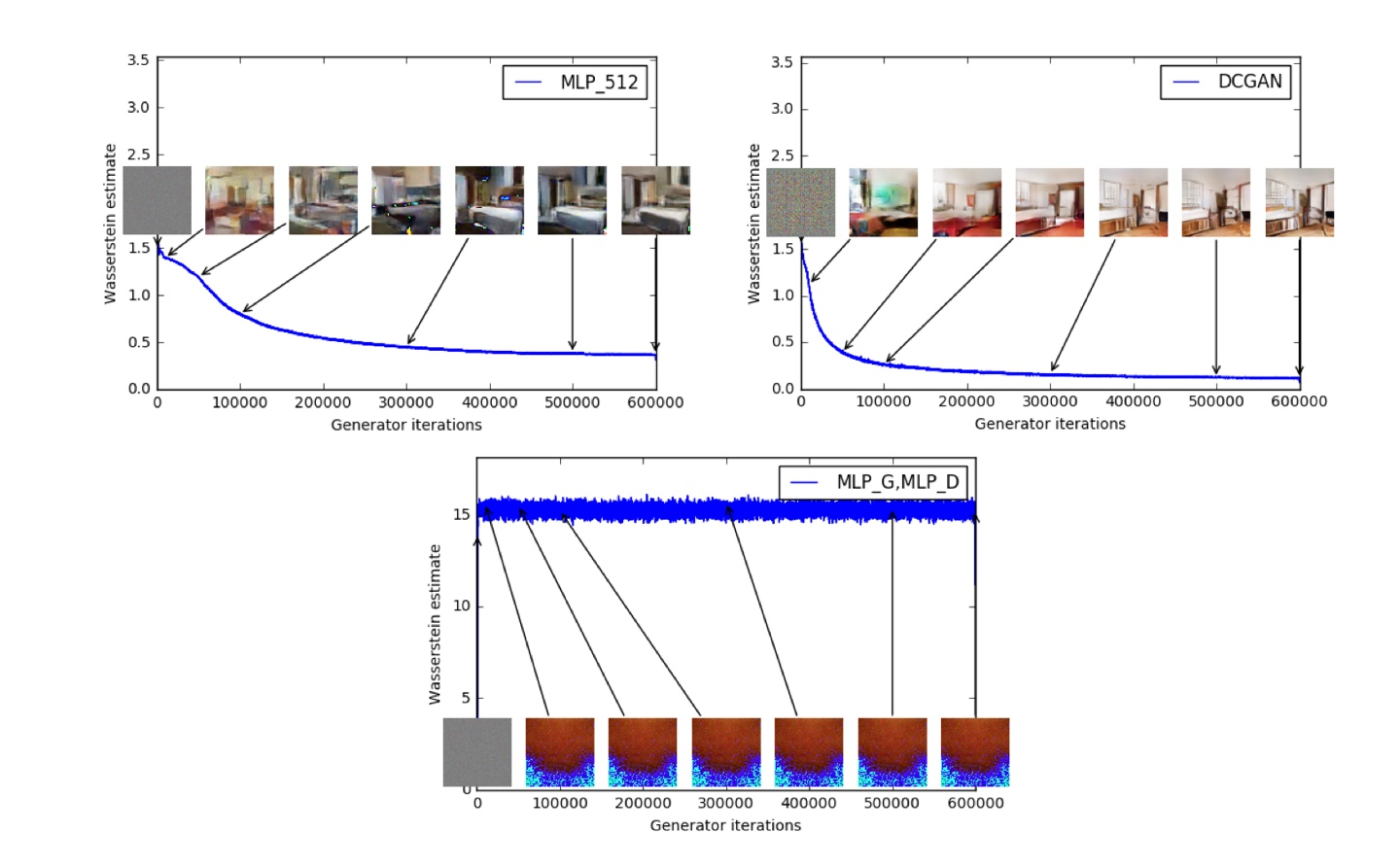
상단 두 개의 그래프는 Discriminator 대신 critic을 적용한 것인데, 왼쪽은 Generator로 MLP(Multi Layer Perceptron), 오른쪽은 standard DCGAN을 활용한 결과입니다. 학습이 진행될수록 Loss가 점차 줄어들고, Sample의 질이 점차 좋아지는 것을 확인할 수 있습니다.
→ Lower Error, Better Sample Quality = Training Successed 😄
하단 그래프는 Discriminator와 Generator 모두 MLP를 사용한 결과입니다. 학습이 진행되더라도 Loss가 일정하고, Sample이 여전히 알아보기 어렵습니다.
→ Training Failed 😥
Improved Stability

Figure 5 : DCGAN Generator로 학습시킨 경우이며, 왼쪽 WGAN과 오른쪽 standard GAN 모두 좋은 성능을 보입니다.
Figure 6 : DCGAN Generator로 학습시키되, Batch Normalization을 수행하지 않고 모든 Layer에서 필터 개수를 고정시킨 경우(전체 Parameter 수를 줄인 경우)입니다. 왼쪽 WGAN은 여전히 질 좋은 Sample을 생성하는 반면, 오른쪽 standard GAN은 그렇지 못합니다.
Figure 7 : Generator를 MLP+ReLU로 변형하여 학습시킨 결과입니다(DCGAN보다 Inductive Bias 부족한 상황). 왼쪽 WGAN은 다양한 Sample을 생성해낸 반면, 오른쪽 standard GAN은 겹치는 Sample들을 생성해냈음을 확인할 수 있습니다(Mode Collapse 문제 개선 여부와 관련).
2. CGAN (Conditional Generative Adversarial Nets)
Introduction
Unconditioned Generative Model 하에서는 생성되는 종류(mode)를 제어할 방법이 없습니다. 이때, Class label 등에 기반하여 추가 정보가 생긴다면 데이터 생성 과정을 제어할 수 있게 됩니다.
본 논문에서는 Conditional Adversarial Net을 구축하는 방법을 다룹니다.
Conditional Adversarial Nets
GAN의 Generator와 Discriminator 모두에 추가 정보 y가 주어진다면, 조건부 생성모델을 만들 수 있습니다. (Generator과 Discriminator의 input layer에 y를 추가하는 방식입니다.)
따라서 Conditional Adversarial Net의 목적함수는 GAN의 목적함수에서 input이 조건부로 바뀐 형태로 정의됩니다.
-
GAN 목적함수 :
-
Conditional Adversarial Net 목적함수 :
아래는 Conditional Adversarial Net의 구조입니다.
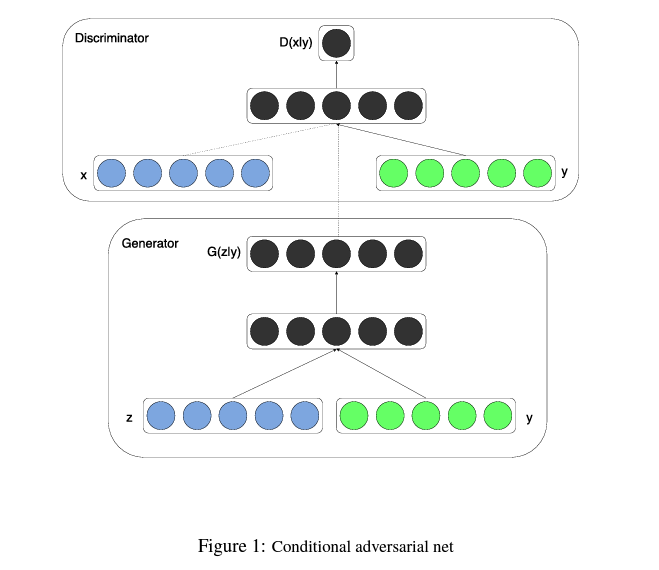
Experimental Results
Unimodal (Unique mode)
Class label에 기반하여 MNIST 데이터셋으로 Conditional Adversarial Net을 학습시키는 과정입니다.
Generator와 Discriminator 모두에 생성하고 싶은 숫자에 대한 One-Hot vector를 conditioning합니다.
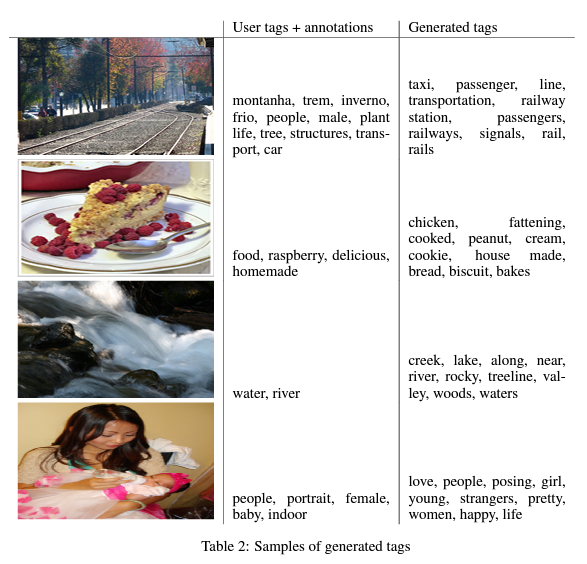
아래 이미지는 각 행이 하나의 label에 대해 conditioned되어 생성된 sample들입니다.

Multimodal (Multi modes)
이번에는 다른 양식의 추가 데이터를 제공합니다.
아래는 각 이미지에 대해 사용자가 부여한 tag와 Conditional Adversarial Net이 생성한 tag를 비교한 결과입니다.
Code Review
코드 출처 : https://github.com/znxlwm/pytorch-generative-model-collections/blob/master/CGAN.py
import utils, torch, time, os, pickle
import numpy as np
import torch.nn as nn
import torch.optim as optim
from dataloader import dataloader
class generator(nn.Module):
# Network Architecture is exactly same as in infoGAN (https://arxiv.org/abs/1606.03657)
# Architecture : FC1024_BR-FC7x7x128_BR-(64)4dc2s_BR-(1)4dc2s_S
def __init__(self, input_dim=100, output_dim=1, input_size=32, class_num=10):
super(generator, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.input_size = input_size
self.class_num = class_num
self.fc = nn.Sequential(
nn.Linear(self.input_dim + self.class_num, 1024),
nn.BatchNorm1d(1024),
nn.ReLU(),
nn.Linear(1024, 128 * (self.input_size // 4) * (self.input_size // 4)),
nn.BatchNorm1d(128 * (self.input_size // 4) * (self.input_size // 4)),
nn.ReLU(),
)
self.deconv = nn.Sequential(
nn.ConvTranspose2d(128, 64, 4, 2, 1),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.ConvTranspose2d(64, self.output_dim, 4, 2, 1),
nn.Tanh(),
)
utils.initialize_weights(self)
def forward(self, input, label):
x = torch.cat([input, label], 1)
x = self.fc(x)
x = x.view(-1, 128, (self.input_size // 4), (self.input_size // 4))
x = self.deconv(x)
return x
class discriminator(nn.Module):
# Network Architecture is exactly same as in infoGAN (https://arxiv.org/abs/1606.03657)
# Architecture : (64)4c2s-(128)4c2s_BL-FC1024_BL-FC1_S
def __init__(self, input_dim=1, output_dim=1, input_size=32, class_num=10):
super(discriminator, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.input_size = input_size
self.class_num = class_num
self.conv = nn.Sequential(
nn.Conv2d(self.input_dim + self.class_num, 64, 4, 2, 1),
nn.LeakyReLU(0.2),
nn.Conv2d(64, 128, 4, 2, 1),
nn.BatchNorm2d(128),
nn.LeakyReLU(0.2),
)
self.fc = nn.Sequential(
nn.Linear(128 * (self.input_size // 4) * (self.input_size // 4), 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, self.output_dim),
nn.Sigmoid(),
)
utils.initialize_weights(self)
def forward(self, input, label):
x = torch.cat([input, label], 1)
x = self.conv(x)
x = x.view(-1, 128 * (self.input_size // 4) * (self.input_size // 4))
x = self.fc(x)
return x
class CGAN(object):
def __init__(self, args):
# parameters
self.epoch = args.epoch
self.batch_size = args.batch_size
self.save_dir = args.save_dir
self.result_dir = args.result_dir
self.dataset = args.dataset
self.log_dir = args.log_dir
self.gpu_mode = args.gpu_mode
self.model_name = args.gan_type
self.input_size = args.input_size
self.z_dim = 62
self.class_num = 10
self.sample_num = self.class_num ** 2
# load dataset
self.data_loader = dataloader(self.dataset, self.input_size, self.batch_size)
data = self.data_loader.__iter__().__next__()[0]
# networks init
self.G = generator(input_dim=self.z_dim, output_dim=data.shape[1], input_size=self.input_size, class_num=self.class_num)
self.D = discriminator(input_dim=data.shape[1], output_dim=1, input_size=self.input_size, class_num=self.class_num)
self.G_optimizer = optim.Adam(self.G.parameters(), lr=args.lrG, betas=(args.beta1, args.beta2))
self.D_optimizer = optim.Adam(self.D.parameters(), lr=args.lrD, betas=(args.beta1, args.beta2))
if self.gpu_mode:
self.G.cuda()
self.D.cuda()
self.BCE_loss = nn.BCELoss().cuda()
else:
self.BCE_loss = nn.BCELoss()
print('---------- Networks architecture -------------')
utils.print_network(self.G)
utils.print_network(self.D)
print('-----------------------------------------------')
# fixed noise & condition
self.sample_z_ = torch.zeros((self.sample_num, self.z_dim))
for i in range(self.class_num):
self.sample_z_[i*self.class_num] = torch.rand(1, self.z_dim)
for j in range(1, self.class_num):
self.sample_z_[i*self.class_num + j] = self.sample_z_[i*self.class_num]
temp = torch.zeros((self.class_num, 1))
for i in range(self.class_num):
temp[i, 0] = i
temp_y = torch.zeros((self.sample_num, 1))
for i in range(self.class_num):
temp_y[i*self.class_num: (i+1)*self.class_num] = temp
self.sample_y_ = torch.zeros((self.sample_num, self.class_num)).scatter_(1, temp_y.type(torch.LongTensor), 1)
if self.gpu_mode:
self.sample_z_, self.sample_y_ = self.sample_z_.cuda(), self.sample_y_.cuda()Reference
- WGAN
★임성빈님, 'Wasserstein GAN 수학 이해하기 I'
전현규님, '십분딥러닝_16_WGAN (Wasserstein GANs)'
ratsgo's blog
https://jonathan-hui.medium.com/gan-wasserstein-gan-wgan-gp-6a1a2aa1b490- CGAN
https://greeksharifa.github.io/generative%20model/2019/03/19/CGAN/
https://github.com/znxlwm/pytorch-generative-model-collections/blob/master/CGAN.py
3개의 댓글
좋은 강의 감사합니다.
WGAN
- GAN의 BCE loss를 최적화 하는 것은 KL-divergence와 Jensen-Shannon Divergence를 최소화 하는 것과 같은데, 두 metric은 모델과 데이터의 분포가 너무 상이하면, gradient vanishing 문제가 발생하거나 발산할 수 있습니다.
- 또한 GAN은 생성자와 판별자의 학습 불균형으로 인해 모드 붕괴 현상을 불러일으킬 수 있습니다.
- WGAN은 분포가 상이하더라도 좀 더 세밀하게 그 차이를 측정할 수 있는 EM-distance(Wasserstein Distance)를 기반으로 cost function을 정의합니다.
- cost 계산을 위해선 립시츠 조건을 만족해야하는데, 저자는 이를 위해서 경험적으로 가중치의 범위를 제한했습니다.(weight clipping)
-WGAN은 다른 기존 GAN보다 안정적인 학습을 수행합니다.
CGAN
- CGAN은 GAN의 input에 라벨 정보를 추가한 모델입니다.
GAN의 세계는 넓고도 깊군요..
WGAN
- GAN의 접근방식은 실제 데이터의 분포를 결정하는 잠재벡터의 분포를 가정하고 입력으로 하여 generator를 학습시킵니다.
- 하지만 GAN은 generator와 discirminator의 학습 난이도 차이가 커서 mode collapse 문제가 발생합니다.
- mode collapse란 generator가 전체 데이터 분포를 고르게 찾지 않고, 하나의 mode만 집중적으로 생성하도록 학습되는 현상입니다.
- wgan에서는 EM distance를 이용한 metric으로 이를 해결합니다.
- 기존 gan의 metric인 kl divergence와 js divergence는 모두 두 분포의 차가 커질 수록 그래디언트를 효과적으로 생성하지 못하는 문제가 있습니다.
- EM distance는 이에 비해 분포의 차에 비례한 그래디언트를 안정적으로 생성하여 학습에 도움이 됩니다.
- 실제로 EM distance를 이용하면 계산량도 많고 구현도 어려워서 Kantorovich-Rubinstein Duality Theorem을 이용하여 간단하게 식을 구성할 수 있습니다.
- 그 결과 dcgan과 비교하여 inductive bias도 학습되고, 안정적으로 학습이 일어나는 모습을 보였습니다.
CGAN
- 기존의 GAN 모델들은 mode를 제어할 수 있는 방법이 없습니다.
- CGAN은 우리가 생성하고자 하는 y에 대한 추가정보를 입력으로 사용하여 조건부 생성모델을 구성하였습니다.
- 기본적으로 one hot vector의 형식으로 입력되어 임베딩 레이어를 통과하는 방식 등을 사용합니다.

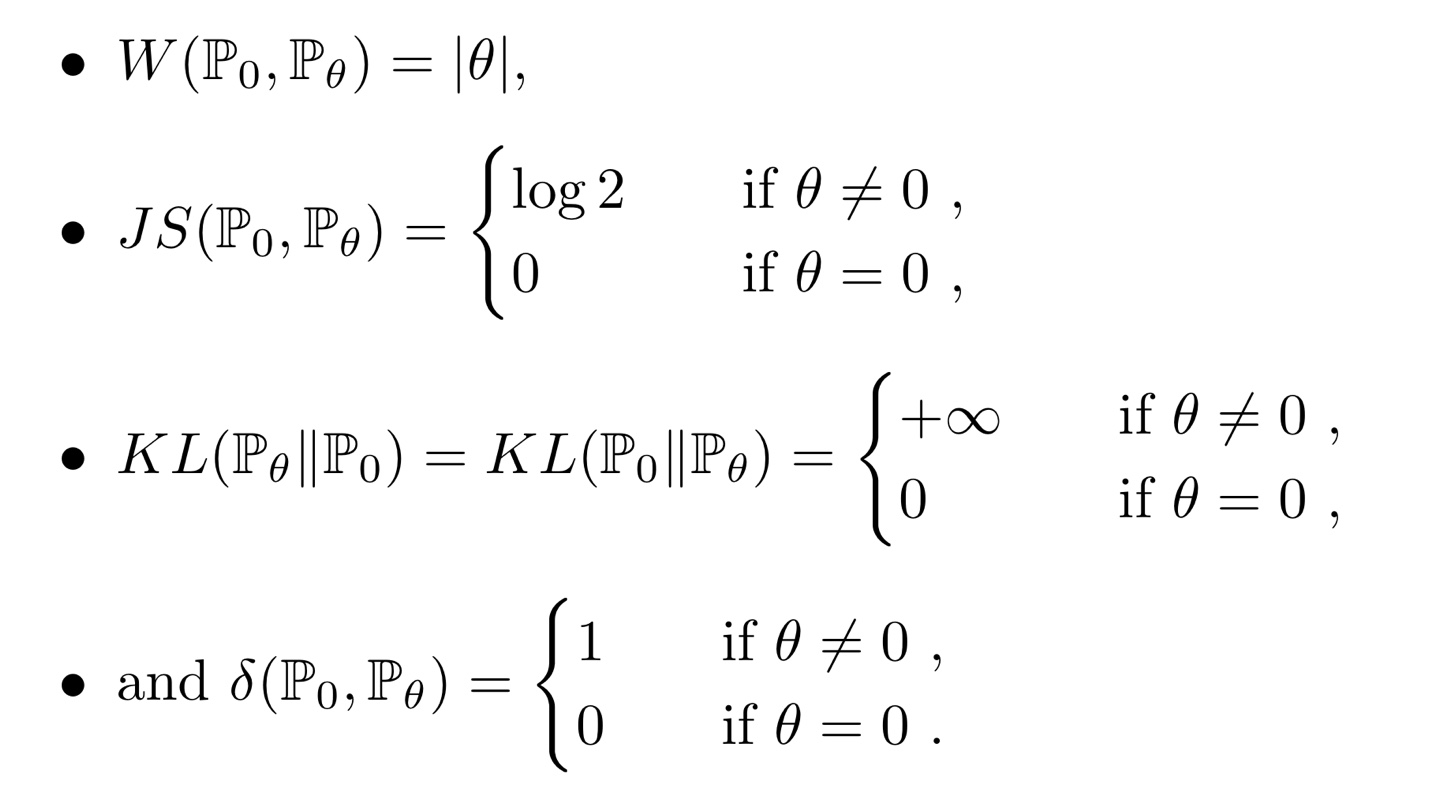




강의 잘 들었습니다.
WGAN
CGAN