작성자: 투빅스 15기 김태희

Contents

0. Intro
1. Intuition
2. Decomposition
3. Relevence Propagation
4. Application

[2주차]CNN 필터시각화에서는 피처 맵을 시각화해 이미지로부터 모델의 성능을 미치는 부분에 대해 알아보았다. 하지만 이러한 방법은 output에 가까운 레이어일수록 추상화 수준이 높아 해석이 어렵다는 단점이 있다. 본 게시글에서는 신경망 모델에의 결과를 역추적해 각 입력에 대한 기여도를 계산하는 LRP(Layer-wise Relevance Propagation)에 대해 알아보고자 한다.

0. Intro

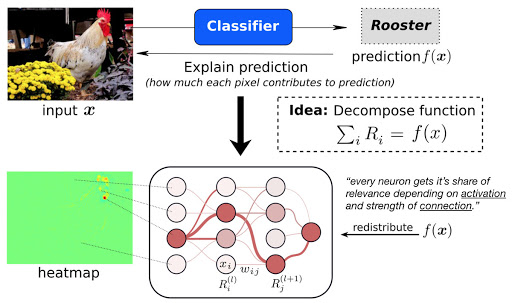
기본적으로 인공지능 모델은 블랙박스이기 때문에 어떠한 결정에 대해 그 이유를 알 수 없다. 이를 사람이 이해할 수 있는 형태로 설명하고자 다양한 AI 기술이 나오고 있으며, 이를 XAI(Explainable AI)라고 한다.

위와 같이 어떠한 사진이 있고 학습된 신경망 모델이 이를 '수탉'이라고 분류했을 때, LRP 알고리즘은 모델이 데이터의 어떤 부분을 보고 해당 결과를 도출해 내었는지 히트맵 형식으로 알려주는 방법이다. 위 사진에 LRP를 적용한 결과를 보았을 때 모델이 우측 상단의 데이터를 기반으로 수탉이라 분류했다는 것을 알 수 있다. 이처럼 히트맵 형식으로 각 데이터의 기여도를 계산할 시 앞의 피처맵 기법보다 해석을 오인할 가능성이 적다.

1. Intuition

1-1. Relevance Propagation & Decomposition

LRP는 타당성 전파(Relevance Propagation)와 분해(Decomposition) 방법을 사용해 모델을 해부한다. 출력값에서부터 시작해 타당성 점수 또는 기여도라 불리는 relevance score를 입력단 방향으로 계산해 나가며 그 비중을 분배하는 방법이다.

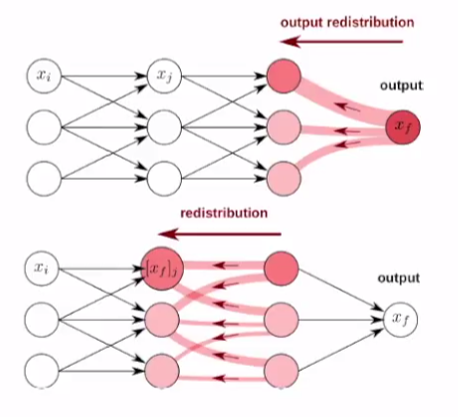
• 각 layer마다 분해(decompose)
• 기여도(relevance)를 output layer부터 top-down 형식으로 재분배
• 재분배하는 과정에서 기여도(relevance) 값은 보존되어야 한다
  -> 각 layer에서의 기여도 값의 합은 모두 동일해야 한다

1-2. Mathematically

임의의 $d$ 차원의 입력 값 $x = (x_1, x_2, ... x_i, ... x_d)$ 에 대해 모델이 $f(x)$라는 값을 도출해 내었을 때, $x$ 의 각 차원에 대해 relevance score를 계산해보자!

$f(x) = \sum_{i=1}^{d}R_i$

• $R_i$: relevance score, 출력 $f(x)$ 를 얻기 위해 입력 이미지의 각 pixel들이 기여하는 바
• 예측값 $f(x)$는 각각의 입력에 대한 기여도(relevance score)로 분해(decompose)

1-3. Neural Net

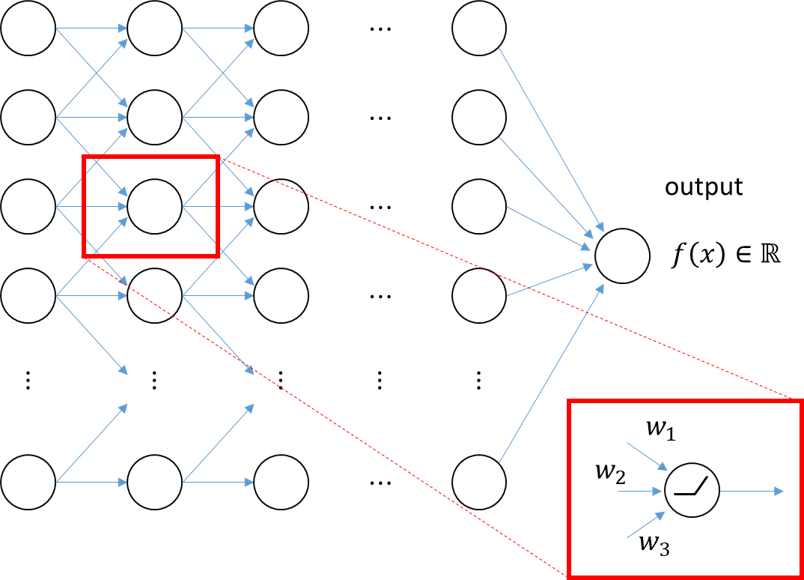
궁극적으로 신경망 모델에 LRP를 적용하고자 했을 때, 한 뉴런에서 출력값을 입력층들에게 어떻게 분해해서 배분할지를 결정해야 한다.

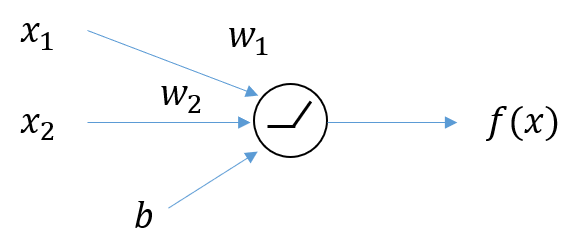
하나의 출력값을 가지는 노드에 대해서 먼저 살펴보자. 위의 노드는 두 개의 입력값과 하나의 bias로부터 하나의 출력값을 가진다. 출력값 $f(x)$는 입력값 $(x_1, x_2)$로부터 얻어지므로 $y = f(x) = f(x_1, x_2)$ 로 나타낼 수 있다.

Relevance Score $x$ 가 출력에 얼마나 영향을 주는가는 $x$의 값이 변화했을 때 $f(x)$값의 변화량을 통해 예측 가능

변화량? -> 미분

따라서 출력값 $f(x)$에 대해 각 입력 $(x_1, x_2)$의 기여도는 다음과 같이 편미분을 사용하여 나타낼 수 있다.
$\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}$

출력값을 기여도로 분해($f(x)$ -> $\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}$)하기 위해 함수를 미분계수들의 급수로 나타내는 Taylor Series를 사용한다.

2. Decomposition

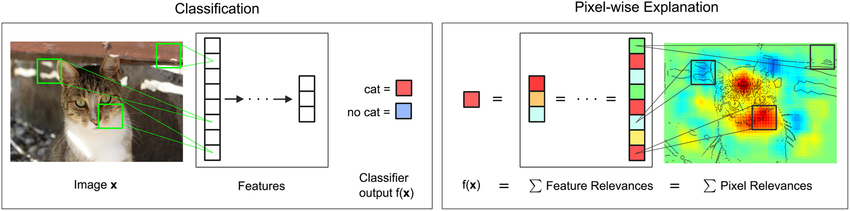
분해(Decomposition)은 입력된 각 피처가 결과에 얼마나 영향을 미치는지 해체하는 방법이다. 분해 과정을 거친 후 이미지의 특정 픽셀이 결과값을 도출하는데 긍정적인 영향이 있는지 또는 부정적인 영향이 있는 지를 알 수 있다.

위의 이미지에서는 이미지를 '고양이'로 분류를 하는데 각 hidden layer에서 계산한 기여도를 토대로 해당 이미지의 피처들을 모델이 어떻게 받아들였는지를 히트맵으로 도식화한 것이다. 결정에 도움이 된 영역은 빨간색으로, 도움이 되지 않은 부분은 파란 색으로 표시된 것을 통해 얼굴 부분의 이마, 코, 입 주변의 픽셀들이 결과에 영향을 많이 주었다는 것을 확인할 수 있다.

3. Relevance Propagation

3-1. Taylor Series

타당성 전파(Relevance Propagation)과정에서 기여도를 계산할 때 Taylor Series 사용
임의의 매끄러운 함수 $f(x)$ 및 실수 $a$에 대해 $f(x)$의 Taylor Series 는 다음과 같이 나타낼 수 있다.

$f(x) = \sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n$

$=f(a) + \frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \cdots$

1차 Taylor Series: $f(x) = f(a) + \frac{d}{dx}f(x)\big|_{x=a}(x-a) + \epsilon$

• $\epsilon$ : 2차 이상의 항들
• $\frac{d}{dx}f(x)\big|_{x=a}(x-a)$ : relevance score 결정
  x가 변할 때 $f(x)$ 가 얼마나 변하는지 알 수 있음
• $f(a)=0$, $\epsilon=0$일 때 relevance를 계산할 수 있음

Taylor Series를 앞서 나온 입력값이 2개이고 출력이 1개인 Neural Net에 적용해 보자. 여기서 입력값이 여러 개이므로 multivariate function에 대한 taylor series를 활용해야 한다.

$d$차원의 입력 값들에 대한 1st order Taylor Series:
$f(\pmb{x}) = f(\pmb{a}) + \sum_{p = 1}^{d}\frac{\partial \pmb{f}}{\partial x_p}\big|_{\pmb{x}=\pmb{a}}(\pmb{x} - \pmb{a}) + \epsilon$

앞서 1차원의 1st order Taylor Series에서 전미분이 편미분으로, $d$차원에 대해 summation을 해준 것 이외 동일한 형태를 가진다는 것을 알 수 있다.

$\sum_{p = 1}^{d}\frac{\partial \pmb{f}}{\partial x_p}\big|_{\pmb{x}=\pmb{a}}(\pmb{x} - \pmb{a})$
$x_p$가 변했을 때, $f(x)$가 얼마나 변하는지 나타내주는 항

3-2. Deep Taylor Decomposition

$f(\pmb{x}) = f(\pmb{a}) + \sum_{p = 1}^{d}\frac{\partial \pmb{f}}{\partial x_p}\big|_{\pmb{x}=\pmb{a}}(\pmb{x} - \pmb{a}) + \epsilon$

$f(a)=0$, $\epsilon=0$일 때 relevance를 계산할 수 있다.

$f(x) = f(a) + \sum_{i=1}^{d}\frac{\partial f}{\partial x_i}\big|_{x_i = a_i}(x_i-a_i) + \epsilon$
$= \sum_{i=1}^{d}\frac{\partial f}{\partial x_i}\big|_{x_i = a_i}(x_i-a_i)$
$= \sum_{i=1}^{d}R_i$

출력을 Relevance Score로만으로 분해하자!

Neural Net에서 $f(x)$의 출력값이 나오기 전에 activation funciton ReLU를 사용한다고 가정했을 때,
$f(x) = \max\left(0, \sum_{i=1}^{2}w_i x_i + b\right)$
의 형식으로 나타낼 수 있다. ReLU함수의 특성상 0보다 작은 경우에는 $f(x) = 0$을 가지기에 0보다 큰 경우일 때에 대해서 계산을 해야 한다.

$f(x) = \sum_{i=1}^{2}w_ix_i + b = f(a) + \sum_{i=1}^{d}\frac{\partial f}{\partial x_i}\big|_{x_i=a_i}(x_i-a_i) + \epsilon$
위의 식은 $f(x)$에 대해 Taylor Decomposition을 해준 것이다.

$f(x) = w_1x_1+w_2x_2+b$

$f(x)$를 각 입력 원소별로 편미분해주면 $\frac{\partial f(x)}{\partial x_1}= w_1, \frac{\partial f(x)}{\partial x_2} = w_2$ 이 나오고, 이 이상의 더 높은 항들에 대해서는 $\frac{\partial ^2 f(x)}{\partial x_1 ^2} = 0, \space \frac{\partial^2 f(x)}{\partial x_1 \partial x_2} = 0, \space \cdots$ 편미분 값이 0인 것을 알 수 있다. 따라서 $\epsilon = 0$

$f(x) = \sum_{i=1}^{2}w_ix_i+b = f(a) + \sum_{i=1}^{2}w_i(x_i-a_i)$

a는 Taylor Series를 활용해 함수를 근사할 때, 그 시작점 $x = a$을 뜻한다. $f(a) = 0$의 제약조건을 만족해야 하기 때문에 조건을 만족시키는 $a$ 값을 찾아 대입을 하면 된다.

4. Application

앞서 예시들과 같이 이미지 Classification시 LRP로 각 원소의 기여도를구하고, 이 값을 통해 벡터값을 추정한 다음 히트맵을 활용해서 모델의 결정을 파헤쳐 볼 수 있다. 이는 Text에서도 가능한데 아래 이미지는 네이버 영화 리뷰 데이터셋에서의 긍정/부정 Classification 결과를 LRP로 해석해 시각화 한 자료이다.

참고자료

• 안재현. (2020). XAI 설명 가능한 인공지능, 인공지능을 해부하다 / 안재현 지음.
• https://angeloyeo.github.io/2019/08/17/Layerwise_Relevance_Propagation.html
• https://itkmj.blogspot.com/2019/08/blog-post.html
• https://lrpserver.hhi.fraunhofer.de/handwriting-classification
• Deep Learning: Theory, Algorithms, and Applications. Berlin, June 2017 - 06. Explaining Decisons of Neural Networks by LRP. Alexander Binder
• Bach S, Binder A, Montavon G, Klauschen F, Müller K-R, Samek W (2015) On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation. PLoS ONE 10(7): e0130140.
• Grégoire Montavon, Sebastian Bach, Alexander Binder, Wojciech Samek, Klaus-Robert Müller (2015) Explaining NonLinear Classification Decisions with Deep Taylor Decomposition