예측 모델의 기본 원리

Chap 4. 가장 훌륭한 예측선

• 딥러닝의 가장 기본적인 두 가지 계산 원리 : 선형 회귀, 로지스틱 회귀

• 선형 회귀 (linear regresstion) : 임의의 직선을 그어 이에 대한 평균 제곱 오차를 구하고, 이 값을 가장 작게 만들어주는 $a$ 값과 $b$ 값을 찾아가는 작업

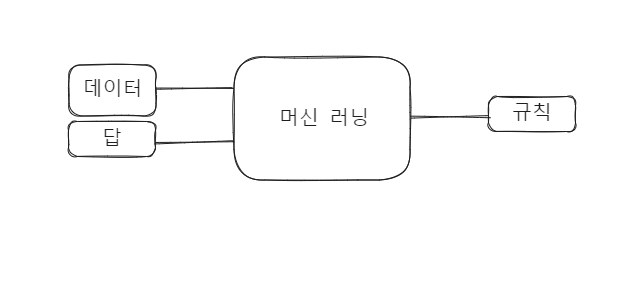
• 머신 러닝과 딥러닝은 '정보' 즉, 독립 변수 $x$ 를 바탕으로 '결과' 즉, 종속 변수 $y$ 를 도출하는 '규칙' 즉, 단순 선형 회귀 (simple linear regresstion) $y = ax + b$ 를 도출해냄.

• Chap 2 에서 보았듯이 $x$ 값이 여러 개 필요하다면 다중 선형 회귀 (multiple linear regression)

머신 러닝과 딥러닝의 동작

---

최소 제곱법 (method of least squares)

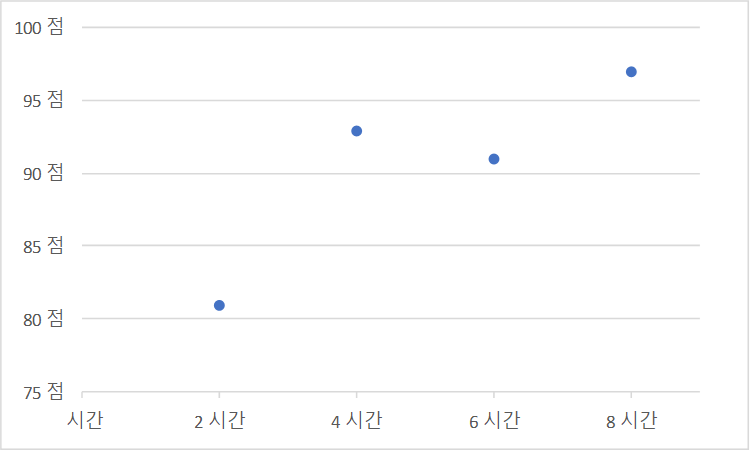
공부한 시간과 중간고사 성적 데이터

공부한 시간과 성적을 좌표로 표현

• $y = ax + b$ 를 데이터에 가장 가깝게 구하기
  $a = \frac{[(x - x의 평균) \times (y - y의 평균)]의 합}{[(x - x 평균)^2]의 합}$
  $b = y의 평균 - (x의 평균 \times a)$

• 기울기 $a$는 실제로 $y$의 증가량을 $x$의 증가량으로 나눈 것이지만, 최소 제곱법에서는 $y$와 $y$의 평균의 차이의 합을 $x$와 $x$의 평균의 차이의 합으로 나눈 것. 그 중 기하 평균 처럼 곱의 합을 제곱의 합으로 나눈다.

• 절편 $b$는 직관처럼 $y - ax$ 즉, $y$의 평균 $- a \cdot x$의 평균.

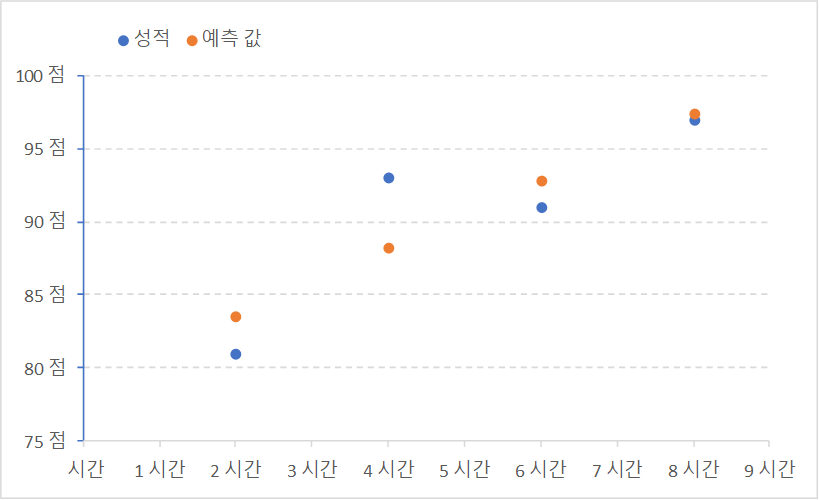
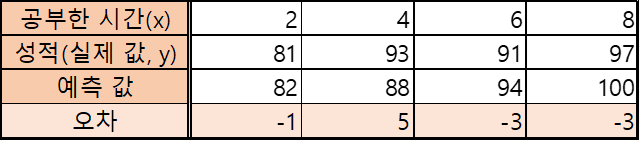
위의 계산 결과를 이용한 데이터는 다음과 같다.

최소 제곱법 공식으로 구한 성적 예측 값

공부한 시간, 성적, 예측 값을 좌료로 표현

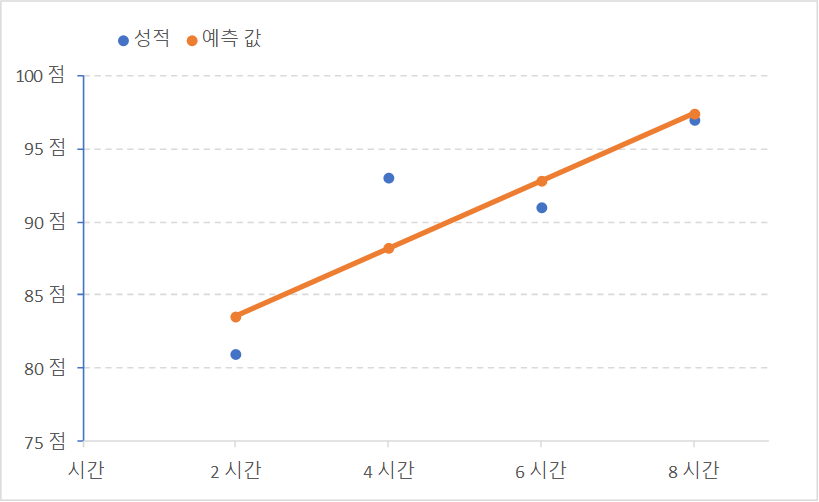
오차가 최저가 되는 직선의 완성

Python

import numpy as np

x = np.array[(2, 4, 6, 8)]
y = np.array([81, 93, 91, 97)]

mx = np,mean(x)
my = np.mean(y)

print("x의 평균값: ", mx)
print("y의 평균값: ", my)

divisor = sum([(i - mx)**2 for i in x])

def top(x, mx, y, my):
    d = 0
    for i in range(len(x)):
        d += (x[i] - mx) * (y[i] - my)
    return d

dividend = top(x, mx, y, my)

print("분모:", divisor)
print("분자:", dividend)

a = dividend / divisor
b = my - (mx*a)

print("기울기 a =", a)
print("y절편 b =", b)

numpy.array : 배열
numpy.mean : 평균

---

평균 제곱 오차 (Mean Square Error, MSE)

임의의 직선 그려 보기

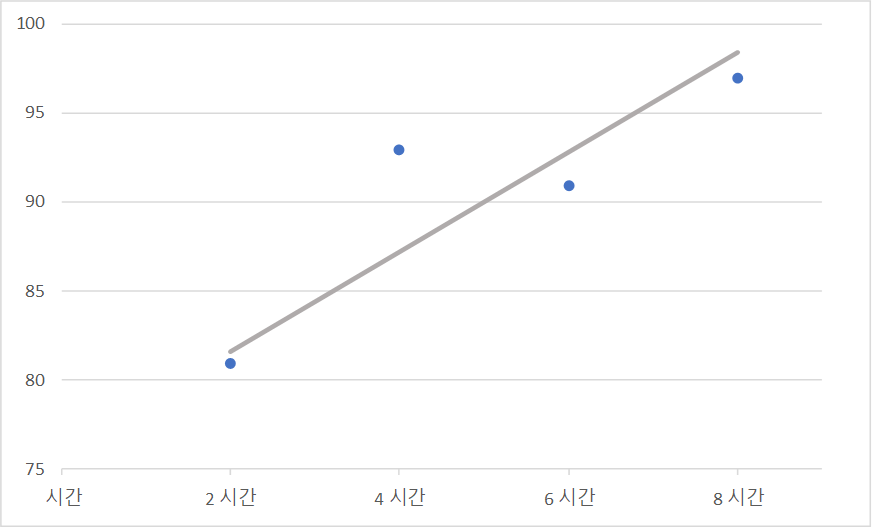임의의 직선 그려 보기

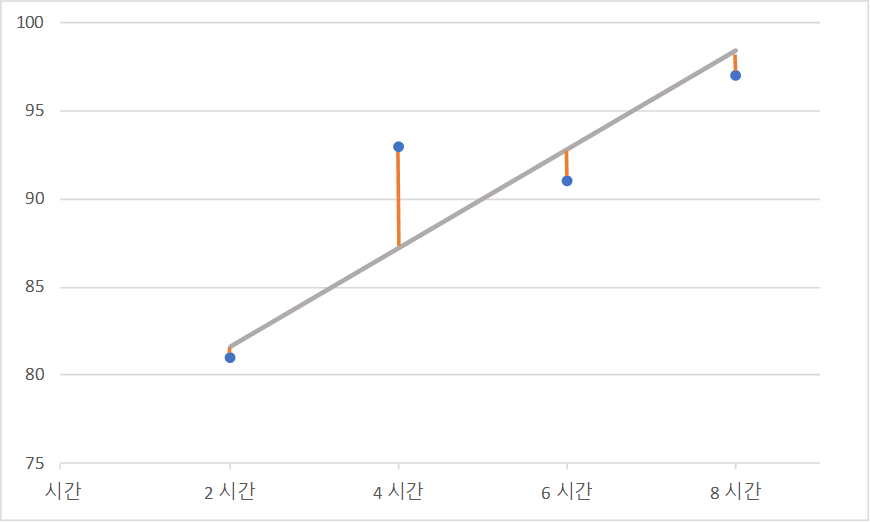$y = 3x + 76$ 의 예측 값 및 오차

평균 제곱 오차(MSE) $= \frac{1}{n} \sum(y_i - \hat{y_i})^2$

Python

import numpy as np

fake_a=3
fake_b=76

x = np.array([2, 4, 6, 8])
y = np.array([81, 93, 91, 97]) 

def predict(x):
    return fake_a * x + fake_b

predict_result = []

for i in range(len(x)):
    predict_result.append(predict(x[i]))
    print("공부시간=%.f, 실제점수=%.f, 예측점수=%.f" % (x[i], y[i], predict(x[i])))

n=len(x)

def mse(y, y_pred):
    return (1/n) * sum((y - y_pred)**2)

print("평균 제곱 오차: " + str(mse(y,predict_result)))

---

Chap 5. 선형 회귀 모델: 먼저 긋고 수정하기

기울기 $a$ 와 오차 사이의 관계 : 이차 함수의 관계

경사 하강법(gradient decent)

이차 함수의 최솟값(=오차의 최솟값)을 구하는 방법 중 하나

• 미분 기울기를 이용하여 0인 지점을 찾는 방법

오차의 변화에 따라 이차 함수 그래프를 만들고 적절한 학습률을 설정해 미분 값이 0인 지점을 구하는 것

선형 회귀 모델에서 적절한 직선의 기울기를 구하는 과정

1. 한 점 $a_1$ 에서의 미분값을 구한다.
2. 기울기의 반대 방향(기울기가 양수면 음의 방향, 음수면 양의 방향)으로 점을 이동시킨다.
3. 이동시킨 $a_2$ 에서 미분값을 구하고 구한 미분 값이 0이 아니면 2 ~ 3의 과정을 반복한다.

학습률(learning rate) : 2번에서 이동시키는 거리
학습률 즉, 미분 후 이동시키는 점이 너무 크면 발산 해버림

절편 b 도 같은 경사 하강법 사용

수식 설정

Python

import numpy as np
import matplotlib.pyplot as plt    # pip install matplotlib

x = np.array([2, 4, 6, 8])
y = np.array([81, 93, 91, 97]) 

plt.scatter(x, y)
plt.show()

a = 0
b = 0

lr = 0.03

epochs = 2001

n=len(x)

for i in range(epochs):                  
    
    y_pred = a * x + b                   
    error = y - y_pred                   
    
    a_diff = (2/n) * sum(-x * (error))   
    b_diff = (2/n) * sum(-(error))       
    
    a = a - lr * a_diff     
    b = b - lr * b_diff     
    
    if i % 100 == 0:        
        print("epoch=%.f, 기울기=%.04f, 절편=%.04f" % (i, a, b))      

y_pred = a * x + b      

plt.scatter(x, y)
plt.plot(x, y_pred,'r')
plt.show()

plt.scatter(x, y) : x, y 의 분포
plt.show() : 그래프로 보여줌
lr : 학습률. 여러 학습률을 적용해 보며 찾아낸 것. 이후에 자동으로 찾아주는 최적화 알고리즘 사용
epochs : 반복 횟수
y_pred : 예측하는 결과
error : 실제 값과 예측값의 차 = 오차
a_diff : 오차 함수를 $a$로 편미분한 값
b_diff : 오차 함수를 $b$로 편미분한 값
a, b : 적절히 이동하기 위해 Ir을 편미분 값에 곱해서 빼줌.(만약 기울기가 음수였다면 더해짐)
plt.plot : x, y, '색'

다중 선형 회귀 모델

공부한 시간, 과외 수업 횟수에 따른 성적 데이터

• $y = a_1x_1 + a_2x_2 + b$

Python

import numpy as np
import matplotlib.pyplot as plt

x1 = np.array([2, 4, 6, 8])
x2 = np.array([0, 4, 2, 3])
y = np.array([81, 93, 91, 97]) 

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter3D(x1, x2, y);
plt.show()

a1 = 0
a2 = 0
b = 0

lr = 0.01 

epochs = 2001 

n=len(x1)

for i in range(epochs):                
    
    y_pred = a1 * x1 + a2 * x2 + b     
    error = y - y_pred                  
    
    a1_diff = (2/n) * sum(-x1 * (error)) 
    a2_diff = (2/n) * sum(-x2 * (error)) 
    b_diff = (2/n) * sum(-(error))       
    
    a1 = a1 - lr * a1_diff  
    a2 = a2 - lr * a2_diff  
    b = b - lr * b_diff     
    
    if i % 100 == 0:        
        print("epoch=%.f, 기울기1=%.04f, 기울기2=%.04f, 절편=%.04f" % (i, a1, a2, b))

print("실제 점수:", y)
print("예측 점수:", y_pred)

텐서플로를 이용한 선형 회귀 모델

• $H(x)$ , 가설 함수(hypothesis) : 문제 해결을 위해 가정하는 식
  $w$ , 가중치(weight) : 변수 $x$에 곱해지는 값, 기울기 $a$
  $b$, 편향(bias) : 데이터의 특성에 따라 따로 부여되는 값, 절편 $b$
  손실 함수(loss function) : 평균 제곱 오차와 같은 실제 값과 예측 값 사이의 오차에 대한 식
  옵티마이저(optimizer) : 경사 하강법과 같은 $H(x)$ 를 찾는 방법

• $y = ax + b$ → $H(x) = wx + b$

Python

import numpy as np
import matplotlib.pyplot as plt

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

x = np.array([2, 4, 6, 8])
y = np.array([81, 93, 91, 97]) 

model = Sequential()

model.add(Dense(1, input_dim=1, activation='linear'))

model.compile(optimizer='sgd', loss='mse')

model.fit(x, y, epochs=2000)

plt.scatter(x, y)
plt.plot(x, model.predict(x),'r')    
plt.show()

hour = 7
prediction = model.predict([hour])

print("%.f시간을 공부할 경우의 예상 점수는 %.02f점입니다" % (hour, prediction))

Dense(unit, input_dim, kernel_initializer, activation)
unit : 출력 값(=성적) 개수
input_dim : 입력 값(=학습 시간) 개수
활성화 함수 : 입력된 값을 다음 층으로 넘길 때 각 값을 어떻게 처리할지를 결정하는 함수
activation : 활성화 함수

linear : 디폴트 값. 입력 값과 가중치로 계산된 결과 값 그대로
sigmoid : 시그모이드 함수. 주로 이진분류
softmax : 소프드맥스 함수. 주로 다중클래스 분류
relu : Rectified Linear Unit 함수. 주로 은닉층

compile(optimizer, loss, metrics)
optimizer : 최적화 방법 설정

sgd : 경사 하강법
rmsprop : RMS 값 이용
adagrad : 학습률을 개별 매개변수에 적응적으로 조정
adadelta : Adagrad의 학습률 감소 버전, 지속적으로 감소하며 학습률 조정에 대한 hyperparameter를 더욱 간단하게 설정
adam : 학습률을 자동으로 조정. 가장 많이 사용하는 최적화 알고리즘 중 하나

loss : 손실 함수설정

mse : 평균 제곱 오차
categorical_crossentropy
binary_crossentropy

metrics : 평가 지표 설정

Python - 다중 선형 회귀 모델

import numpy as np
import matplotlib.pyplot as plt

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

x = np.array([[2, 0], [4, 4], [6, 2], [8, 3]])
y = np.array([81, 93, 91, 97]) 

model = Sequential()

model.add(Dense(1, input_dim=2, activation='linear'))
model.compile(optimizer='sgd' ,loss='mse')

model.fit(x, y, epochs=2000)

hour = 7
private_class = 4
prediction = model.predict([[hour, private_class]])

print("%.f시간을 공부하고 %.f시간의 과외를 받을 경우, 예상 점수는 %.02f점입니다" % (hour, private_class, prediction))

---

Chap 6. 로지스틱 회귀 모델: 참 거짓 판단하기

• 로지스틱 회귀(logistic regression) : 참과 거짓 중 하나를 내놓는 과정

참(0)과 거짓(1)만 있을 경우 linear regression으로 결과를 예측 못함

Linear Function vs Sigmoid Function

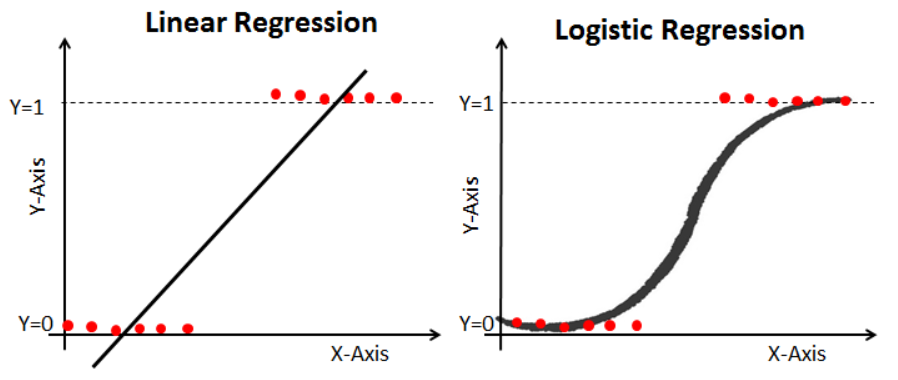시그모이드 함수의 특징

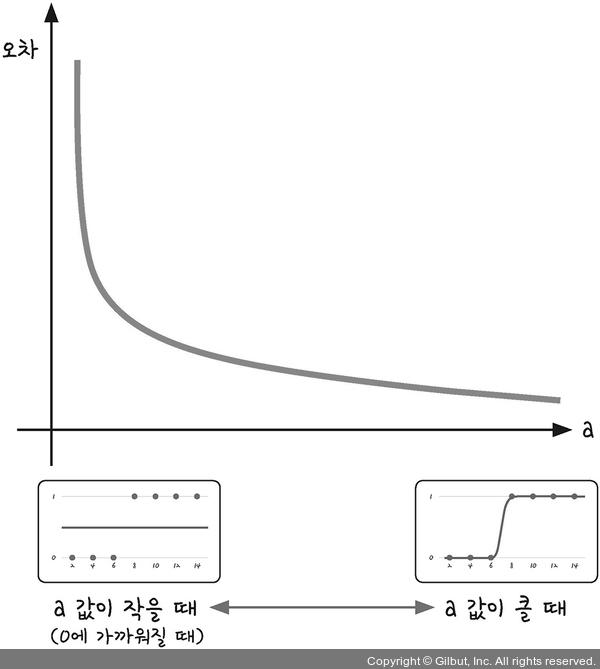
$a$ 에 따른 경사도 차이

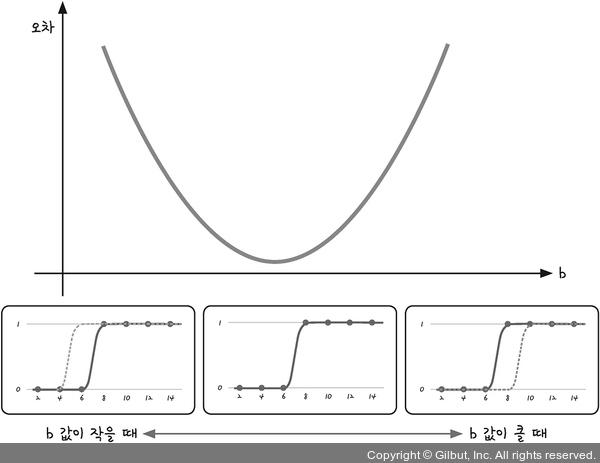
$b$ 는 x축으로의 평행이동

로지스틱 회귀의 오차함수

$a$ 와 오차의 관계

$b$ 와 오차의 관계

• 교차 엔트로피 오차(cross entropy error) : 시그모이드 함수의 손실 함수

$-\{ylogh + (1 - y)log(1-h)\}$

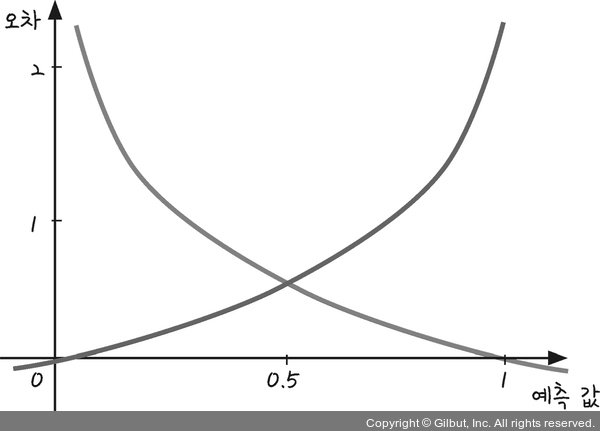Python

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

x = np.array([2, 4, 6, 8, 10, 12, 14])
y = np.array([0, 0, 0, 1, 1, 1, 1]) 

model = Sequential()
model.add(Dense(1, input_dim=1, activation='sigmoid'))

model.compile(optimizer='sgd' ,loss='binary_crossentropy')

model.fit(x, y, epochs=5000)

plt.scatter(x, y)
plt.plot(x, model.predict(x),'r')
plt.show()

hour = 7
prediction = model.predict([hour])

print("%.f시간을 공부할 경우, 합격 예상 확률은 %.01f%%입니다" % (hour, prediction * 100))