안녕하세요. 이번 논문 리뷰는 ShffleNet(ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices)입니다. ShuffleNet은 전에 올려드렸던 MobileNet과 방향성이 같은데요. 즉 파라미터수를 쥐어짜면서, 성능을 높이고자 했습니다. 그러면 어떻게 성능을 올렸을까? 왜 Shffle이라는 이름이 들어갈까요? 그 이유는 밑에서 한번 살펴보도록 하겠습니다.
Introduction
해당 논문은 pointwise group convolution과 channel shuffle을 활용하여 연산량을 줄이고 높은 성능을 보였습니다. Xception, ResNeXt의 경우 Dense한 1x1 conv를 사용했고 전에 포스팅한 MobileNet에서 보았듯, 1x1 conv를 활용하여 파라미터수를 줄일 수 있었지만 결과적으로 모델의 전체 연산량에서 많은 비율을 차지한다는 단점이 존재합니다. 그리고 ResNeXt의 경우 3x3 conv를 하는 layer만 group conv를 적용했는데, 이에 따라 각 Residual unit에 대해 1x1 conv가 전체 연산량의 약 93%를 차지하는 것을 알 수 있습니다. 해당 논문은 AlexNet보다 13배 빠르며 모바일넷보다 뛰어나다고 주장하는 이유인 channel shuffle에 대해서 알아보도록 하겠습니다.
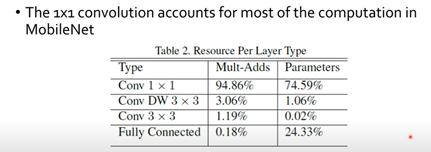
그림1. MobileNet에서 1x1 conv가 연산의 대부분을 차지하는 모습
Pointwise Group Convolution
Pointwise Group Convolution에 앞서서 기본적인 Group Convolution에 대해서 설명을 하고자 합니다. Group Convolution을 사용한 모델 중 유명한 것은 바로 AlexNet입니다. 사실 모델의 성능을 위해서라기보다는, 그 당시에는 GPU의 성능이 그리 좋지 않아서 channel 을 나누어 학습 할 수 밖에 없었다고합니다. 여튼 이렇게 했더니 연산량도 줄어들고 의외로 성능이 더 좋게 나와서 2개의 group으로 나누어 학습을 시키게 된 것입니다.
그래서 shufflenet에서도 이 방법을 사용하게 됩니다. 연산량도 줄이면서 Mobilenet보다 더 좋은 성능을 내보자는 것입니다.
MobileNet에서 보면 , 대부분의 연산량이 1x1 conv에서 나오게됩니다. 따라서 이 부분에서 들어가는 계산 비용을 조금 줄이자는 것 입니다. 그렇게 연산량이 줄어들면, 줄어든 연산량 만큼 channel수를 늘릴 수 있게 되고, 더 많은 channle수는 더 많은 information을 네트워크가 가지게 된다는 것입니다.
논문에서 말하기를 작은 네트워크일수록 많은 feature map 수가 중요하다고 하니, 이 점을 많이 신경쓴것 같습니다.
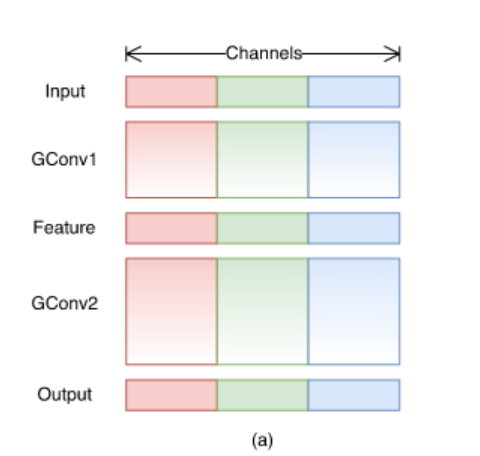
그림2. Group Convolution의 모습
위의 그림은 group conv를 표현한 그림입니다. Input이 들어오면 그 channel들을 group 의 수 만큼 나누어줍니다. 그렇게해서 나누어진 group들마다 각각 Conv를 진행하게 됩니다.
하지만 이렇게 단순하게 group이 나누어진 상태에서 계속 진행하다보면 한 가지 문제점이 생기게 됩니다.
어떤 문제인가하면, 각 group사이의 교류(cross talk)가 없다보니 해당 group들 사이에서만 정보가 흐르게되고 그것은 결국 representation을 약화시키게 되는 것이죠.
다르게 보자면 각 group별로 독립적인 network를 학습시키는 것 처럼 돼버리는것입니다. 결국 더 적은 channel을 가지는 네트워크 여러개를 학습시키는 방법이 되어버릴 수 있는것입니다. 즉, ensemble 비슷하게 되는것입니다.
그래서 이런 문제를 해결하기 위해서 사용하는 방법이 channel shuffle 입니다.
Channel Shuffle
Pointwise Group Convolution을 사용하면, 3x3 conv가 입력 채널 그룹에 대해서만 연산을 수행하고, 그에 관련된 정보만 출력합니다. 채널 간의 정보 교환을 막기 때문에 많은 정보를 이용할 수 없습니다. 따라서 표현력이 약해지게 됩니다. 이 문제를 해결하기위해 Channel Shuffle을 제안합니다.
Channel Shuffle은 3x3 convolution이 서로 다른 그룹에서 입력값을 받도록 합니다. 아래 그림을 살펴보겠습니다. 모든 입력 채널 그룹이 3x3 conv로 전달되네요. 따라서 3x3 conv는 모든 입력 그룹에 해당하는 정보를 활용하여 출력값을 생성합니다.
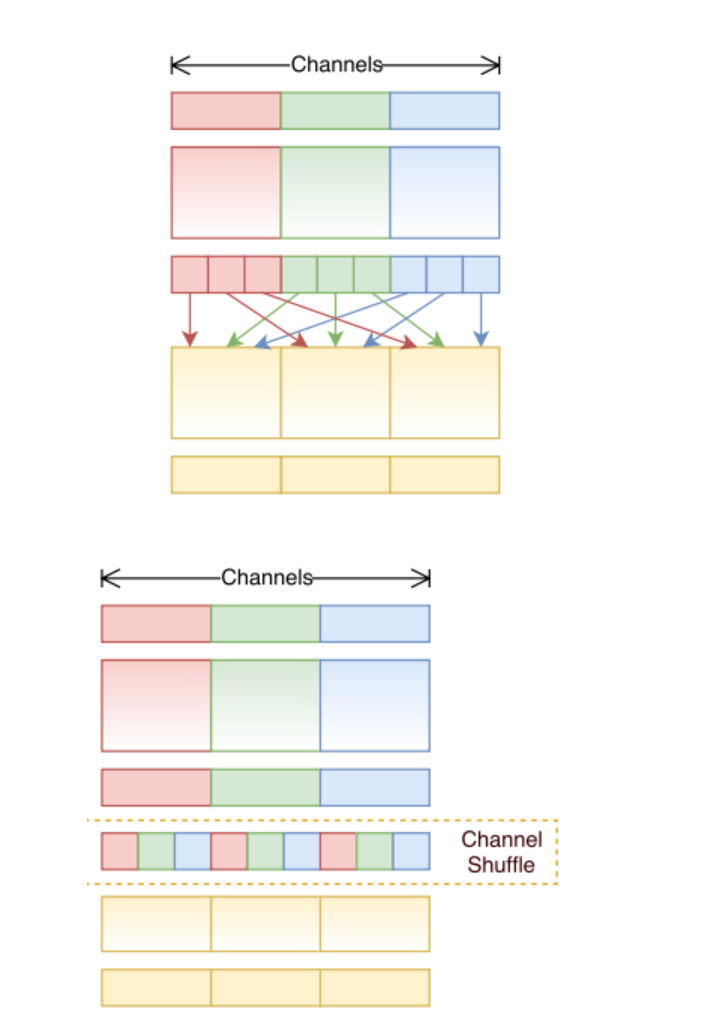
그림3. Channel Shuffle
위 그림은 ShuffleNet에서 구현하는 Channel Shuffle을 나타낸 그림입니다. 1x1 conv layer에서 m개의 채널을 g그룹으로 분할해 하나의 그룹에 n개의 채널을 포함한다고 가정하겠습니다. 1x1 conv는 gxn개의 채널을 출력하고, 이 출력값은 (g, n)으로 reshape 합니다. 이것을 transposing 하고 flattening하여 다음 레이어의 인풋으로 전달합니다.
아래 표는 shuffle을 사용했을 때와 안했을 때의 성능 차이를 비교한 표 입니다.
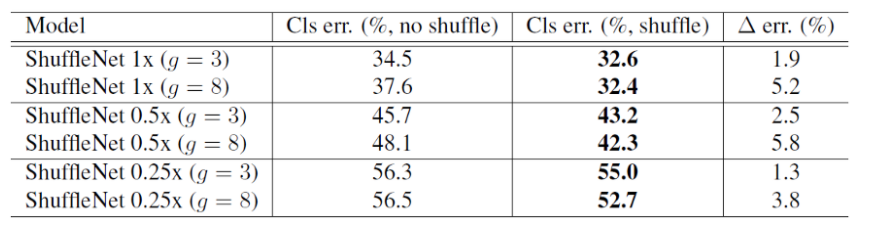
그림4. ShuffleNet을 사용했을 때와 아니었을 때의 차이
ShuffleNet Unit
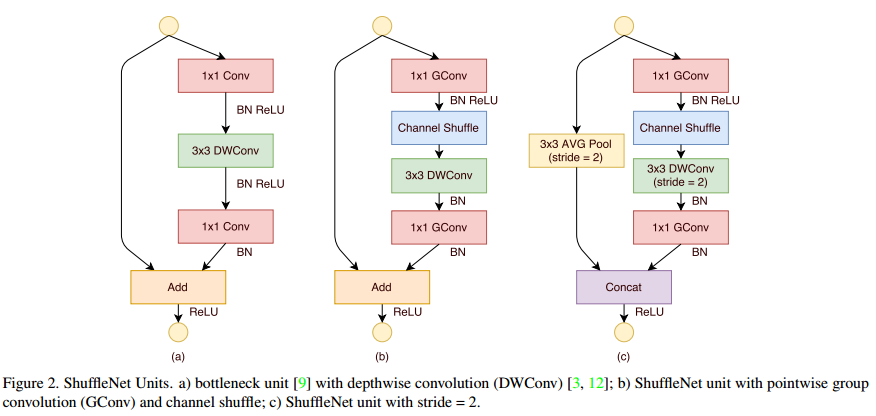
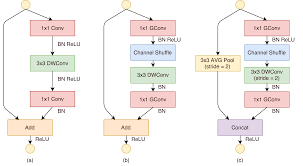
그림5. ShuffleNet Unit 모습
(a)는 Depthwise convolution을 사용하는 BottleNeck 구조입니다.
(b)와 (c)는 ShuffleNet에서 사용하는 unit 입니다. (c)는 down sampling을 할때 사용되며, 3x3 DWConv에서 stride=2를 사용하여 피쳐맵 크기를 반으로 감소합니다. 보통 피쳐맵 크기를 감소할 때, 채널수를 두 배로 해줍니다. SuffleNet에서는 conv 연산으로 채널 수를 확장하지 않고, short cut과 concatenation 하여 채널 수를 확장합니다. short connetion에서도 입력값의 크기를 감소하기 위해 stride=2인 3x3 AVG Pool을 사용합니다.
channel shuffle을 사용하여 다양한 그룹의 채널 정보를 활용해, 3x3 group convolution 문제점을 해결했습니다. 그리고 1x1 pointwise group convolution을 활용해서 연산량에서도 이점을 갖습니다. 따라서 제한된 연산량 내에서 더 많은 피쳐맵을 활용할 수 있습니다.
Architecture
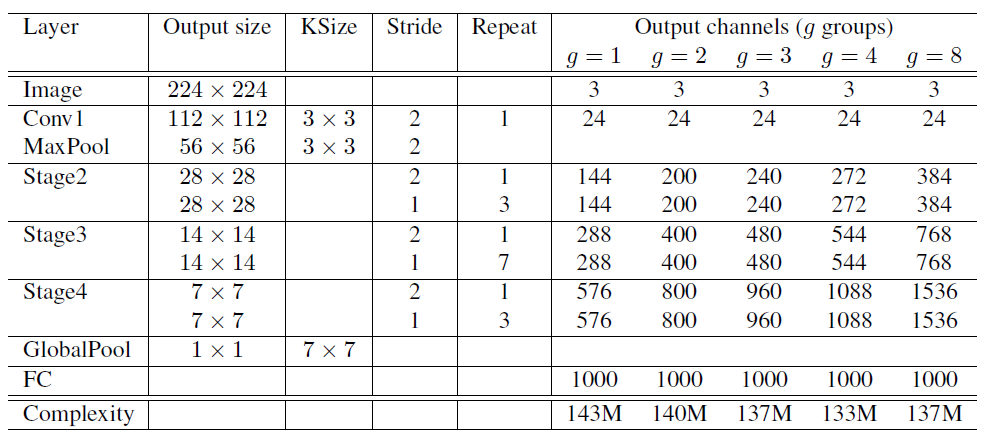
그림6. ShffleNet Architecture
여기서 각 stage에서 Stride 2 라고 되어있는 건 SuffleNet unit (c)를 사용한 것이라고 보면 될 것입니다.
그리고 표 오른쪽에 Output channels 라고 되어있는 건 전체 계산 비용이 거의 변하지 않도록 출력 채널을 정해놓은 것입니다. 보면 그룹수가 많을수록 복잡성 제약에 대해 더 많은 출력 채널(convolutional filter)가 발생합니다. 즉, group을 많이 나누어서 연산량을 줄인만큼 출력 채널(convolutional filter) 수를 늘려줘서 일정한 complexity로 맞춰줍니다.
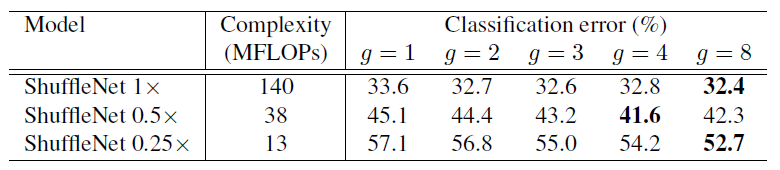
그림7. Classification Error vs Number of Groups g
ShuffleNet 뒤의 1x, 0.5x 는 채널(filter) 수를 scaling 해준 것입니다. 그래서 숫자가 작아질수록 채널 수가 적은 모델이 되는 것입니다. 복잡도도 낮아지고요! 그룹이 많을수록 성능이 좋아지는 것을 알 수 있습니다.
그리고 더 작은 모델일수록 group에 따른 성능의 변화가 큽니다. 이는 작은 모델일수록 channel이 중요한 역할을 한다는 것을 뜻합니다.
해당 논문은 MobileNet과 비슷한 complexity를 맞추어 실험했을 때 더 좋은 성능을 가졌다라는것을 말하고 있습니다. 하지만 메모리 엑세스 문제로 Theoritical Speedup은 x4가 나왔음에도 불구하고 실제 Speedup은 x2.6라고 합니다. 이러한 문제의 해결은 후속 논문인 ShuffleNetV2의 모티브가 됩니다.
