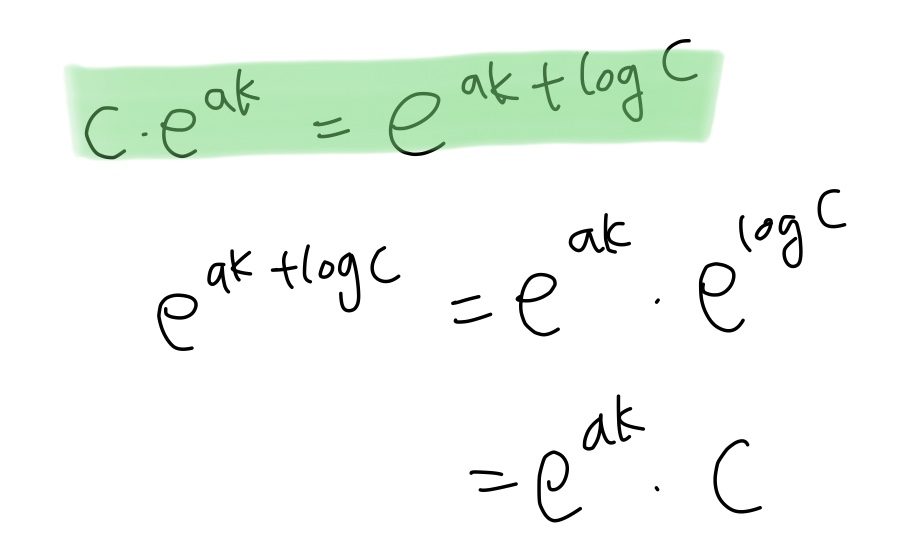[DL] 항등함수와 소프트맥스 함수 구현하기

항등 함수 (identity function)

항등함수는 입력을 그대로 출력한다. 입력과 출력이 항상 같다는 뜻의 항등이다.

소프트맥스 함수 (softmax function)

분류에서 사용하는 소프트맥스 함수의 식은 다음과 같다.

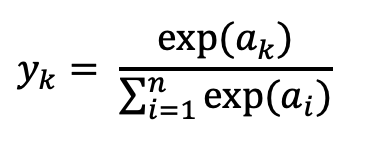
• exp(x): 지수함수
• n: 출력층의 뉴런 수
• $y_k$: 그 중 k번째 출력
• 분자는 입력신호 $a_k$의 지수함수, 분모는 모든 입력 신호의 지수 함수의 합으로 구성

코드 (오버플로우)

def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

구현시 주의점

컴퓨터로 계산할 때 결함이 존재한다. 그 이유는 오버플로우 문제! 소프트맥스 함수는 지수 함수를 사용하는데, 지수 함수란 것이 쉽게 아주 큰 값을 내뱉기 때문에 예를 들면 $e^{20}$은 20000이 넘고, $e^{100}$은 0이 40개 넘는 큰값이 되기도 한다. 이런 큰 값끼리 나눗셈을 하는 경우에는 결과 수치가 불안정해진다.

따라서 이 문제를 해결한 소프트맥스 수식은 다음과 같다.

첫 번째 변형에서는 C라는 임의의 정수를 분자와 분모 양쪽에 곱한다. 그다음으로 C를 지수함수 exp() 안으로 옮겨 $log^C$로 만든다. 마지막으로 $log^C$를 $C'$라는 새로운 기호로 바꾼다.

두번째 식에서 변환과정이 위와 같다! 지수, 로그 공식을 통해 저렇게 됨

위 식은 소프트맥스의 지수 함수를 계산할 때 어떤 정수를 더해도 결과는 바뀌지 않는다는 것이다.

코드 (오버플로우 방지)

def softmax(a):
    c = np.max(a) # overflow 방지를위한 변수
    exp_a = np.exp(a - c) # overflow 대책 
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

그냥 구하면 nan이 출력됨

소프트맥스 함수의 특징

a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y)

print(np.sum(y))

[0.01821127 0.24519181 0.73659691]
1.0

소프트맥스 함수의 출력은 0에서 1.0 사이의 실수이다. 또, 소프트맥스 함수 출력의 총합은 1이다. 출력 총합이 1이 된다는 점은 소프트맥스 함수의 중요한 성질이다.
이 성질로 인해 소프트맥스 함수의 출력을 '확률'로 해석할 수 있다.

위의 출력으로 y[0]의 확률은 0.018(1.8%), y[1]의 확률은 0.245(24.5%), y[2]의 확률은 0.737(73.7%)로 해석할 수 있다. 이 결과 확률들로부터 '2번째 원소의 확률이 가장 높으니 답은 2번째 클래스다' 라고 할 수 있다.

소프트 맥스 함수를 적용해도 각 원소의 대소 관계를 변하지 않는다. 이 는 지수 함수 y=exp(x)가 단조 증가 함수이기 때문읻. a의 원소들 사이의 대소 관계가 y의 원소들 사이의 대소 관계로 그대로 이어진다. 예를 들어 a에서 가장 큰 원소가 2번째 원소이고, y의 가장 큰 원소도 2번째 원소라는 것.

추론 단계에서는 출력층의 소프트맥스 함수를 생략하는 것이 일반적이지만, 신경망을 학습시킬 때는 출력층에서 소프트맥스 함수를 사용한다.