표기법

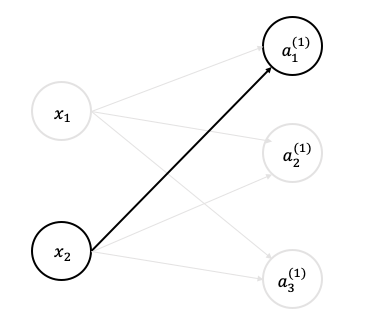
위 그림에서처럼

• 가중치와 은닉층 뉴런의 오른쪽 위에는 (1)이 붙어있다.
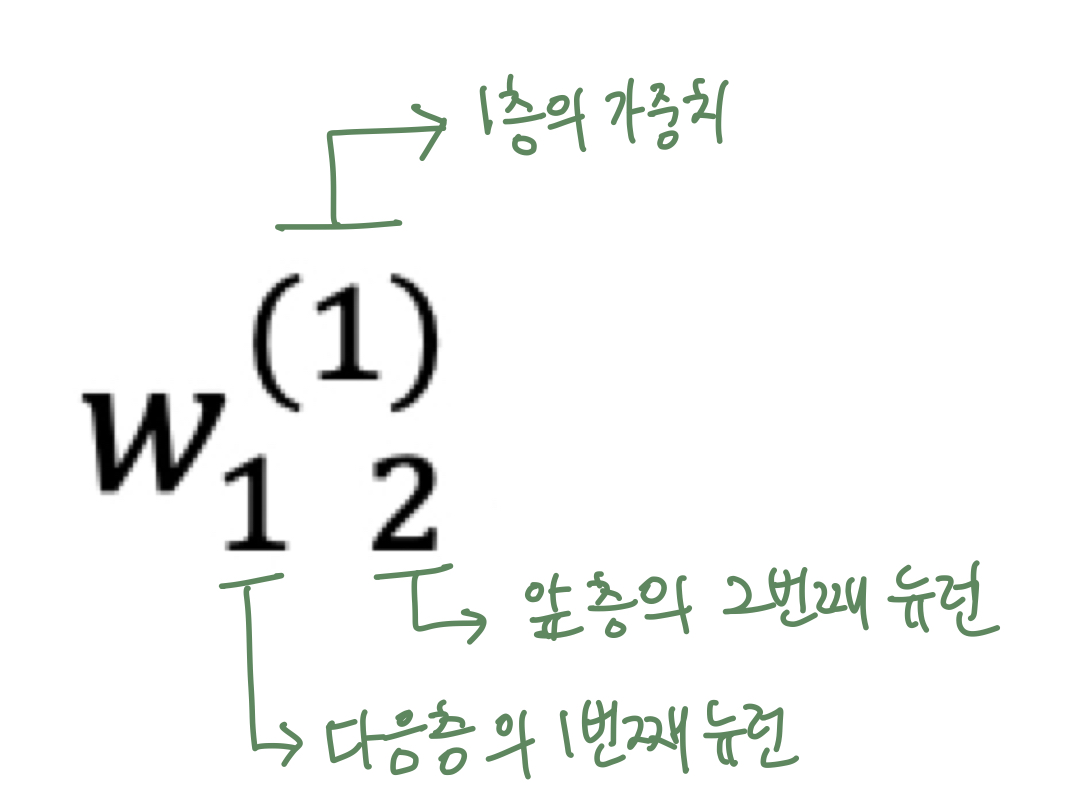
  이는 1층의 가중치, 1층의 뉴런임을 뜻한다.
• 가중치의 오른쪽 아래의 두 숫자는 차례로 다음 층 뉴런과 앞 층 뉴런의 인덱스 번호이다.
  $w^{(1)}_{1 \ 2}$ 의 의미는 앞층의 2번째 뉴런($x_2$)에서 다음층의 1번째 뉴런($a^{(1)}_1$)향할 때의 가중치라는 뜻이다.
• 인덱스 번호는 '다음층 번호, 앞 층 번호'로 순서를 적는다.
  * 그러나 간혹 다른 자료를 볼 때 순서가 다른 경우 존재!
  

각 층의 신호 전달 구현하기

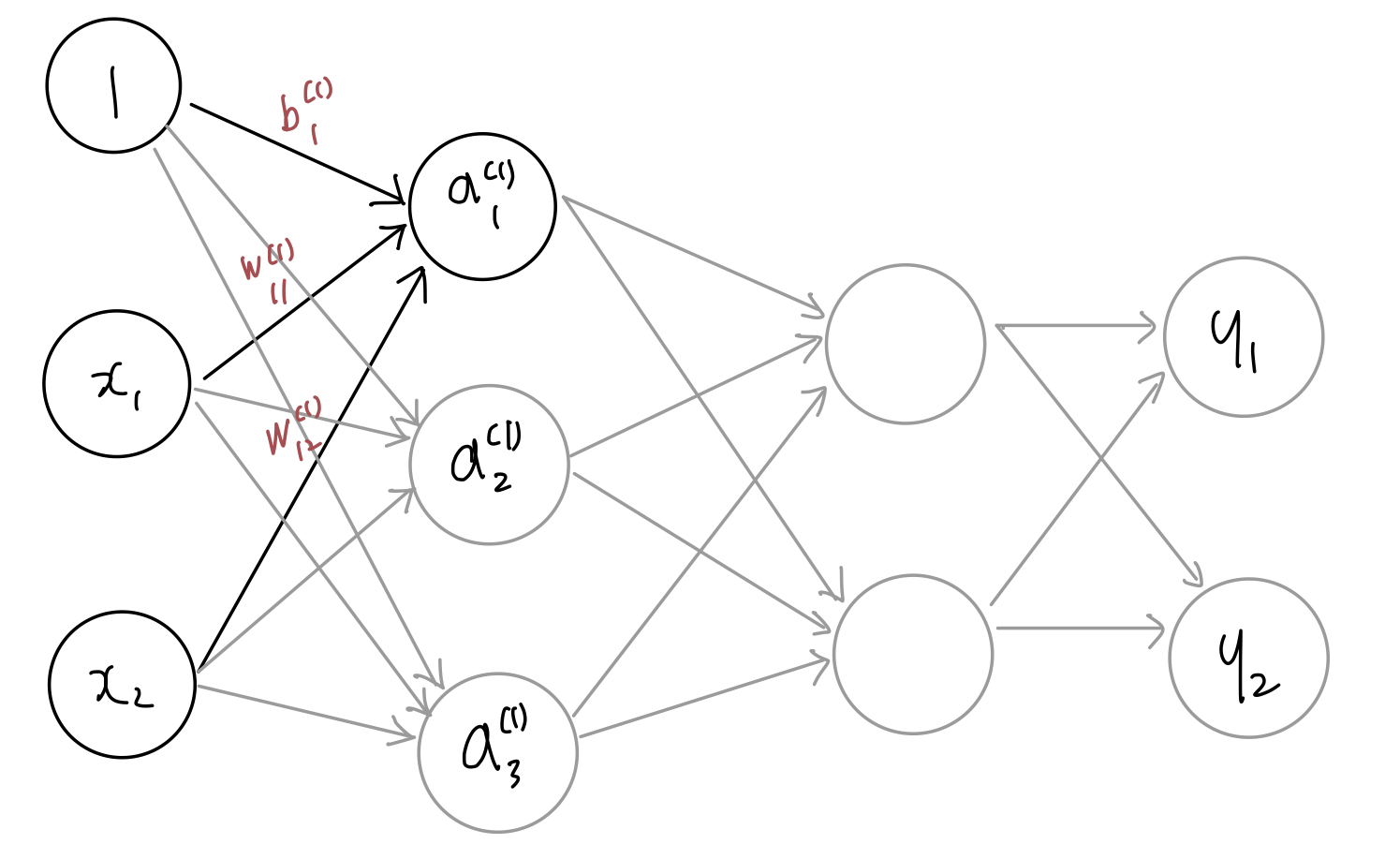
위 그림에서 편향(bias)를 뜻하는 뉴런인 1이 추가되었다. 편향은 오른쪽 아래 인덱스가 하나 밖에 없다! 그 이유는 앞 층의 편향 뉴런(뉴런 1)이 하나뿐이기 때문!

$a^{(1)}_1$을 수식으로 나타내면 다음과 같다.

$a^{(1)}_1 = w^{(1)}_{1 \ 1} + w^{(1)}_{1 \ 2} + b^{(1)}_1$

간소화 한다면 다음과 같다.

$A^{(1)} = XW^{(1)} + B^{(1)}$

코드

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def identity_function(x):
    return x

X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])

print(W1.shape) #2 x 3
print(X.shape)  #1 x 2
print(B1.shape) #1 x 3

A1 = np.dot(X, W1) + B1
Z1 = sigmoid(A1) # 1층 + sigmoid 
print(Z1) #1 x 3

W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) 
B2 = np.array([0.1, 0.2]) 

print(Z1.shape) #1 x 3
print(W2.shape) #3 x 2
print(B2.shape) #1 x 2

A2 = np.dot(Z1, W2) + B2 
Z2 = sigmoid(A2) # 2층 + sigmoid
print(Z2) # 1 x 2

W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])

print(Z2.shape) # 1 x 2
print(W3.shape) # 2 x 2
print(B3.shape) # 1 x 2

A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3) # Y = A3, # 1 x 2
print(Y)

출력

(2, 3)
(2,)
(3,)
[0.57444252 0.66818777 0.75026011]
(3,)
(3, 2)
(2,)
[0.62624937 0.7710107 ]
(2,)
(2, 2)
(2,)
[0.31682708 0.69627909]

마지막에 항등 함수인 identity_function()을 정의하고, 이를 출력층의 활성화 함수로 이용을 한다. 항등 함수는 입력을 그대로 출력하는 함수이다.
여기서 굳이 항등함수를 정의할 필요는 없지만, 흐름과 통일하기 위해 구현하였다고 한다.

출력층의 활성화 함수는 풀고자 하는 문제의 성질에 맞게 정합니다. 예를 들어 회귀에는 항등 함수, 2클래스 분류에는 시그모이드 함수, 다중 클래스 분류에는 소프트맥스 함수를 사용하는 것이 일반적입니다.

구현 정리

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def identity_function(x):
    return x

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) 

출력

[0.31682708 0.69627909]