Regression
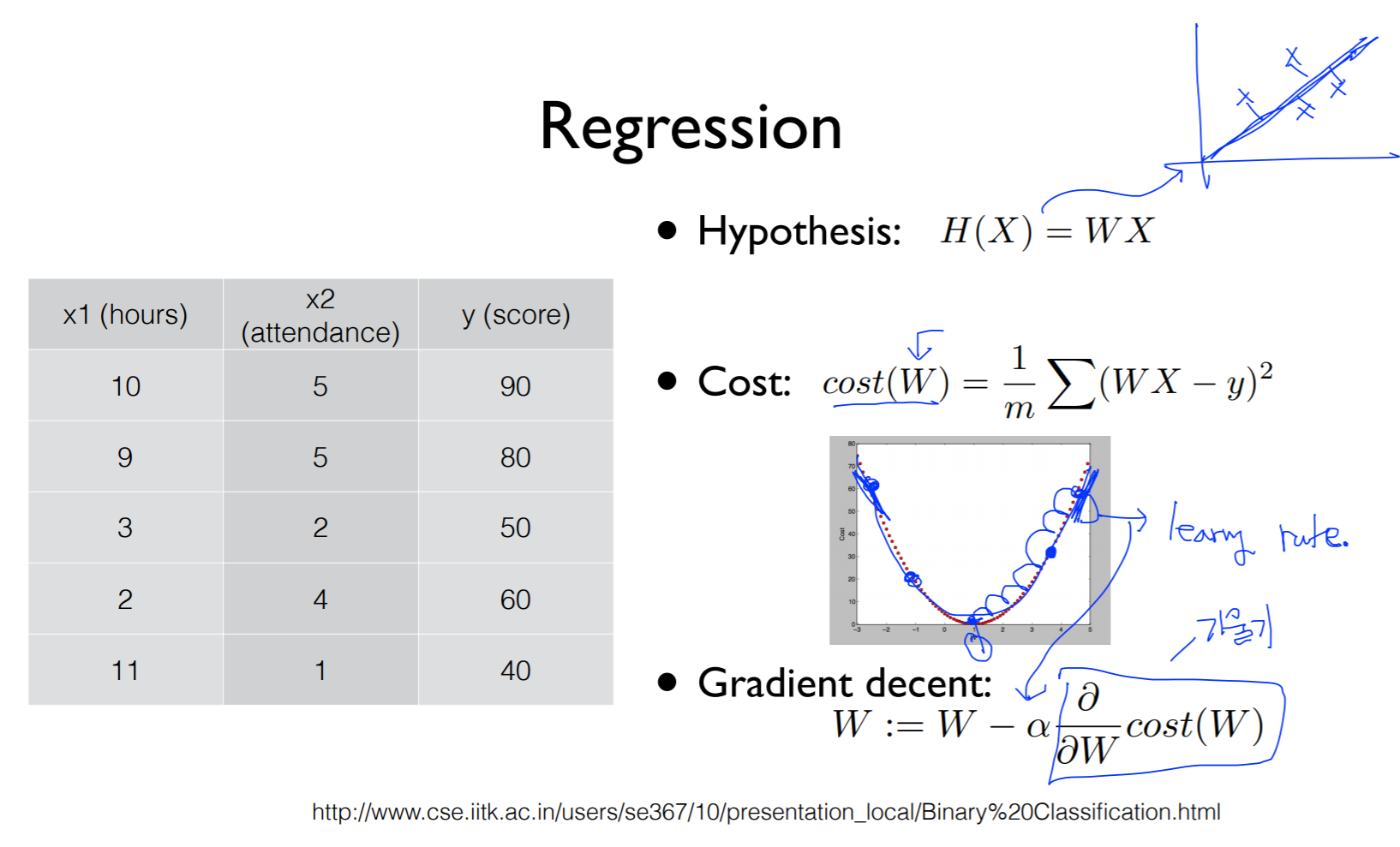
Hypothesis
linear 하게 나타나있음 (식)
Cost
가설로 세운 linear가 얼마나 가깝고 먼가의 값이 cost
학습을 한다는 것은 우리가 가지고 있는 데이터에서 cost가 최소화되는 weight를 찾아야함
Gradient decent
cost 함수를 미분한 값이 기울기
한번에 얼마나 움직일까가 알파 (step size = learning rate)
Classification

binary; 두 개의 category 중 하나를 고르는 것
spam detection: spam인지 아닌지(ham)
facebook feed: 타임라인이 많은데 해당 피드를 볼지 안볼지
credit card fraudulent transaction detection: 신용카드도 도난당하는 경우가 있지만 다르게 돈을 쓰는 경우 잘못되었다고 판단할 수 있음
0, 1 encoding

0, 1 같이 숫자로 encoding 할 수 있음
Radiology
사람의 이미지 판단
finance
주식 시장에서도 사용될 수 있음
Ex
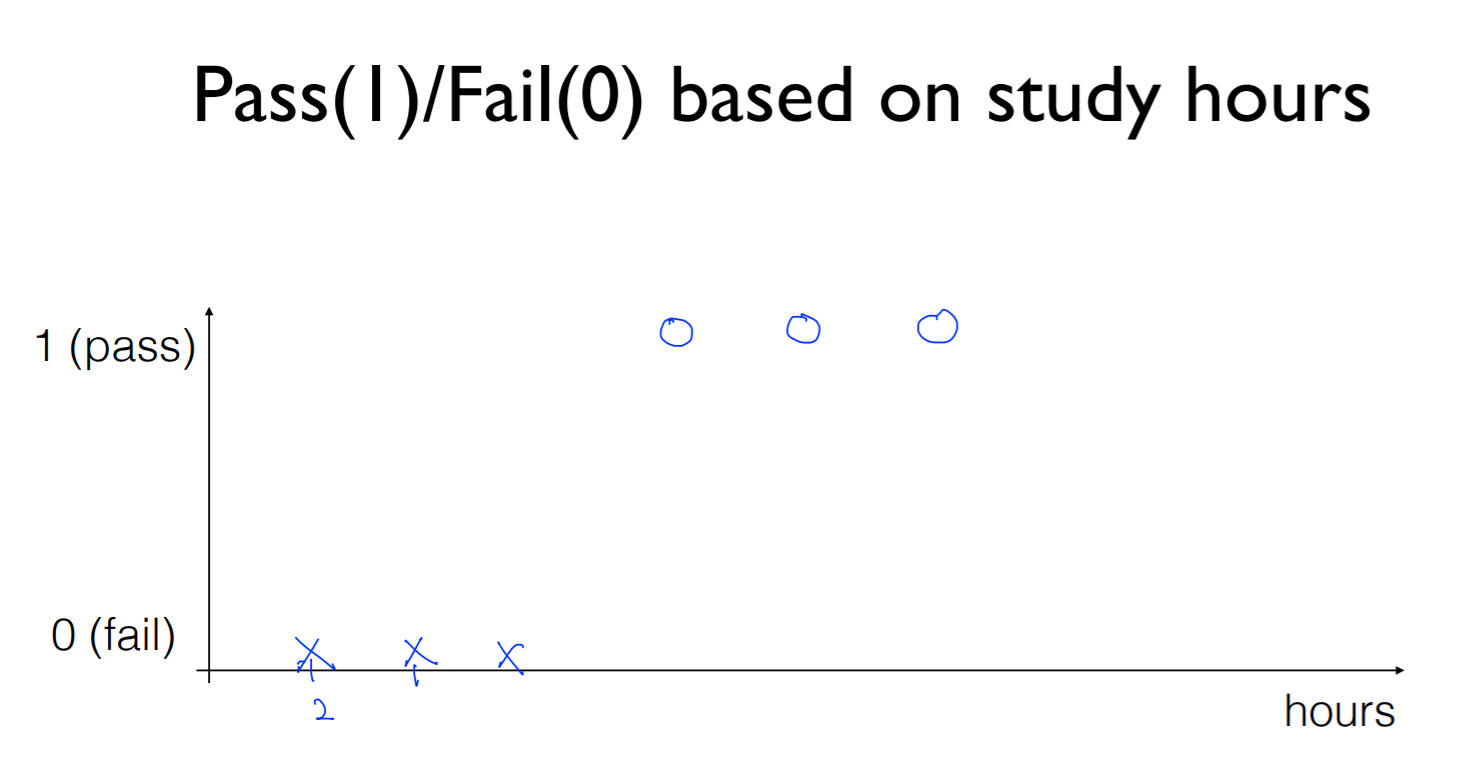
공부 시간에 따라 pass/fail의 여부를 나타낸 그래프
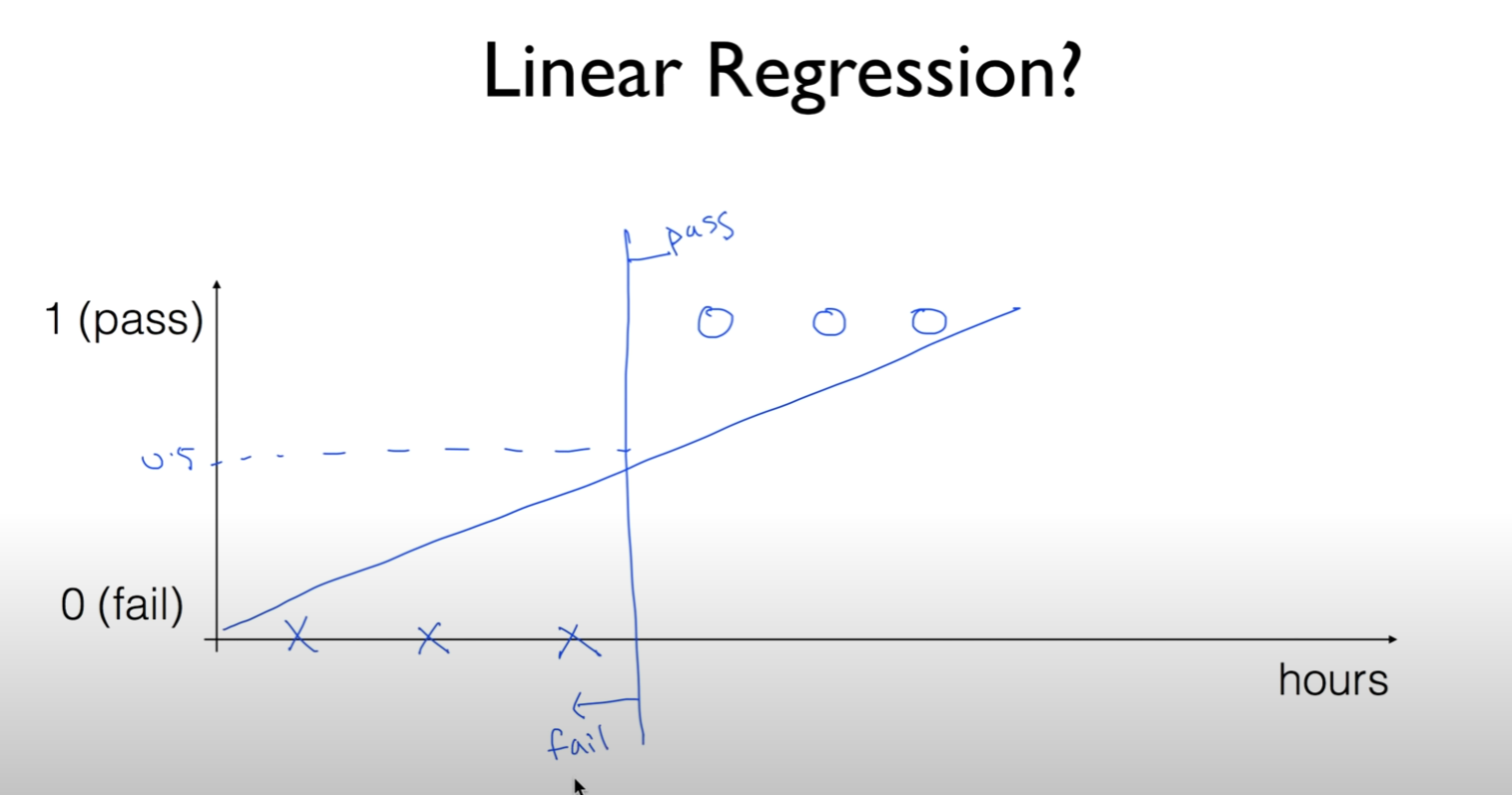
linear 한 그래프를 그려서 (wx) 0.5를 기준으로 pass/ fail을 나눌 수 있음
이러한 경우 50시간 공부한 친구는 pass를 할 가능성이 높음
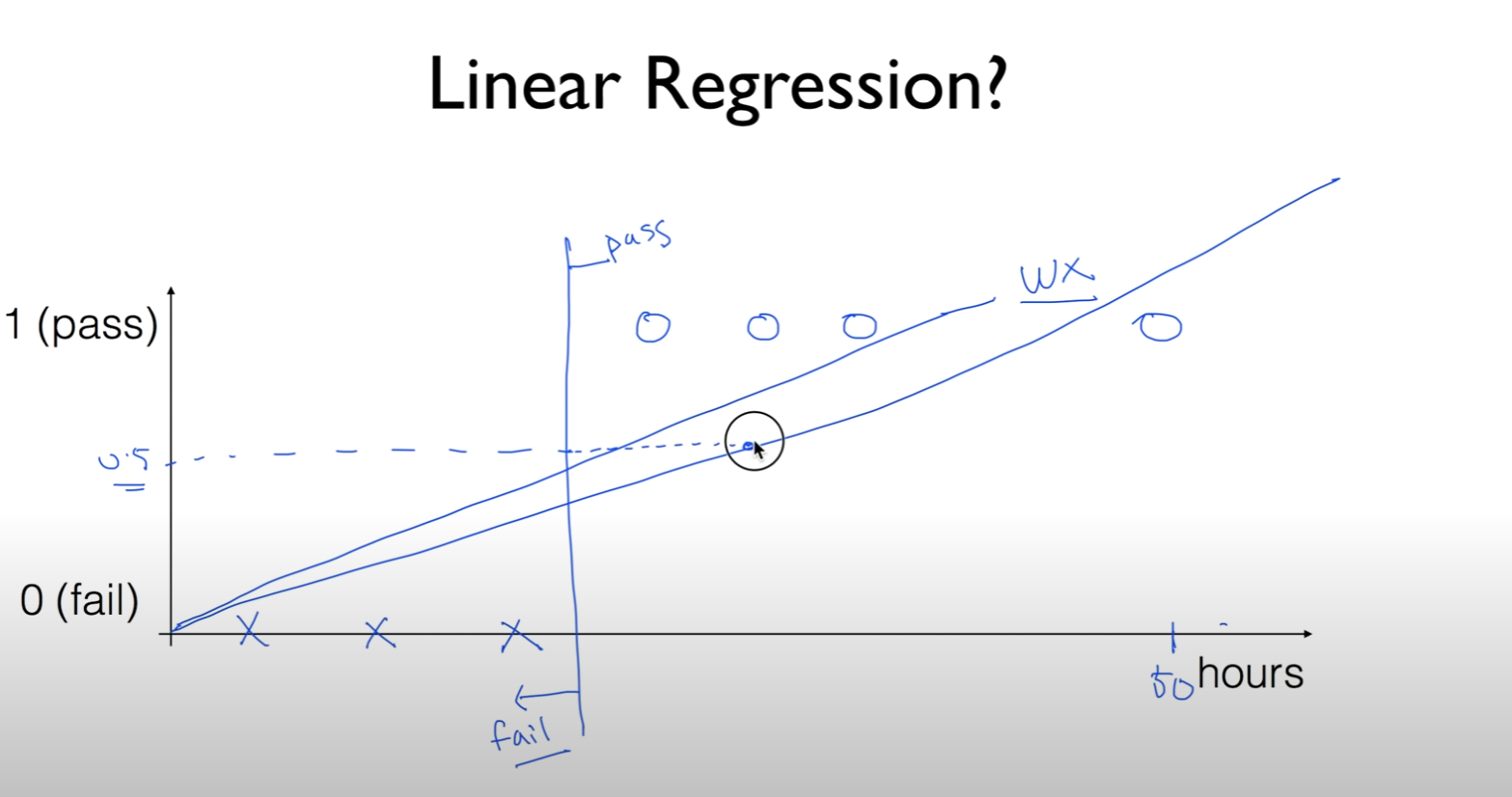
linear한 모델을 학습을 시키면 선과 데이터의 차이를 줄이기 위해서 선이 기울어지는 경우가 생김
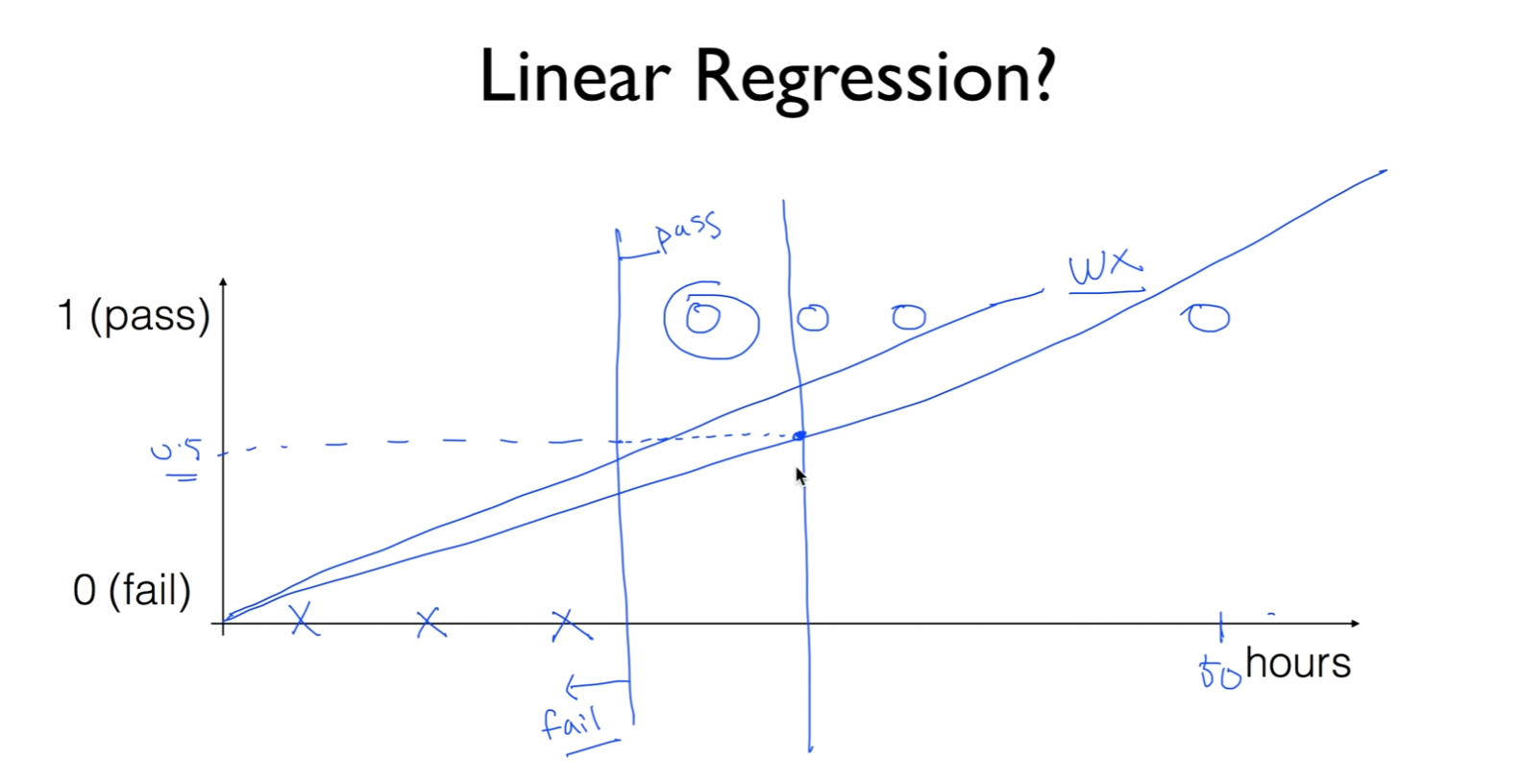
따라서 그 선을 기준으로 0.5를 기준으로 나누게 되면 합격을 한 사람이 불합격의 여부가 나오게 되는 경우도 있음
Linear regression

h(x) = wx + b와 같은 hypersis를 가지게 되면 0보다 크거나 혹은 작거나 1보다 훨씬 큰 값을 가지게 되는 경우가 있음(우리는 여기서 0과 1사이의 값만 나와야함)
예를들어서 가지고 있는 데이터로 학습을 했더니 w = 0.5, b = 0이 나오게 되었고 x = [1, 2, 5, 10, 11] 의 시간이 있다 가정
모델을 학습시킨 후 모델을 통해 예측을 하려고 하는데
x = 100 시간을 공부한 친구를 모델에 적용했을 때 *0.5를 하면 50이 나옴 즉 많은 시간이 나오게 됨 (0-1사이가 안됨)
Logistic Hypothesis
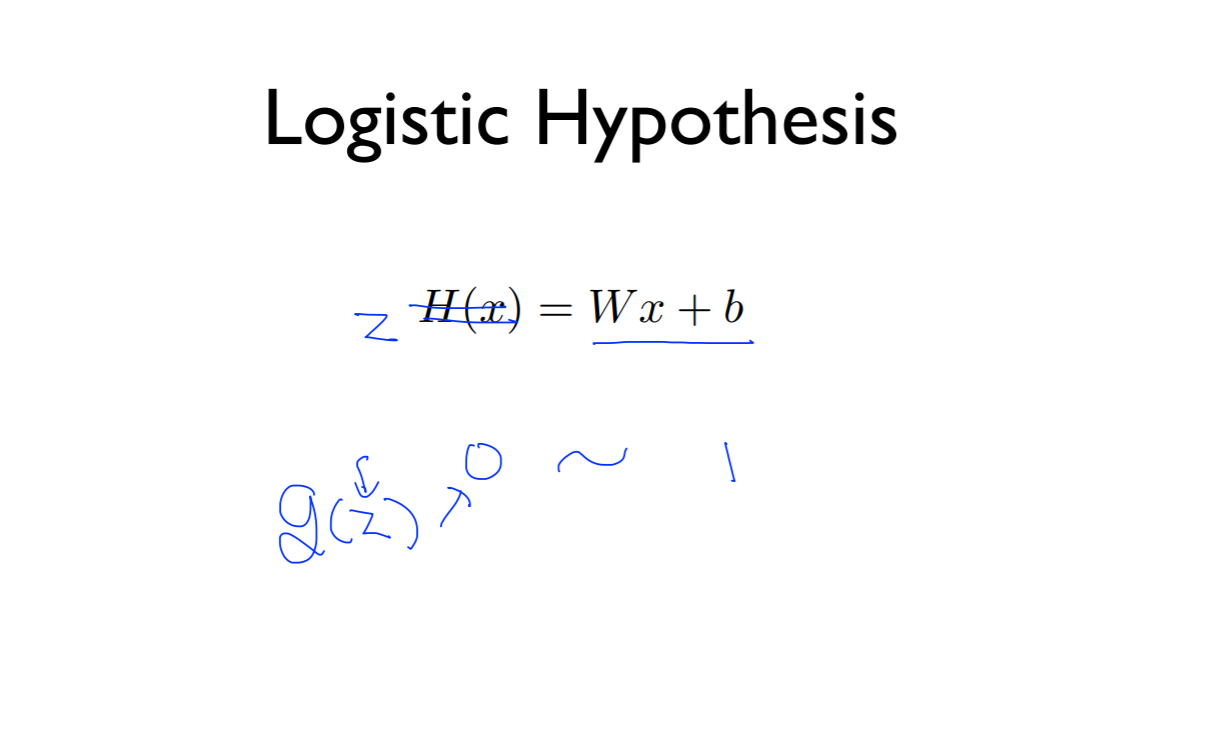
따라서 0, 1 사이의 값이 나오게 하기 위해서 z라는 것을 이용하고 g(z)의 z는 0~1사이의 값만 나오게 된다고 가설을 세움
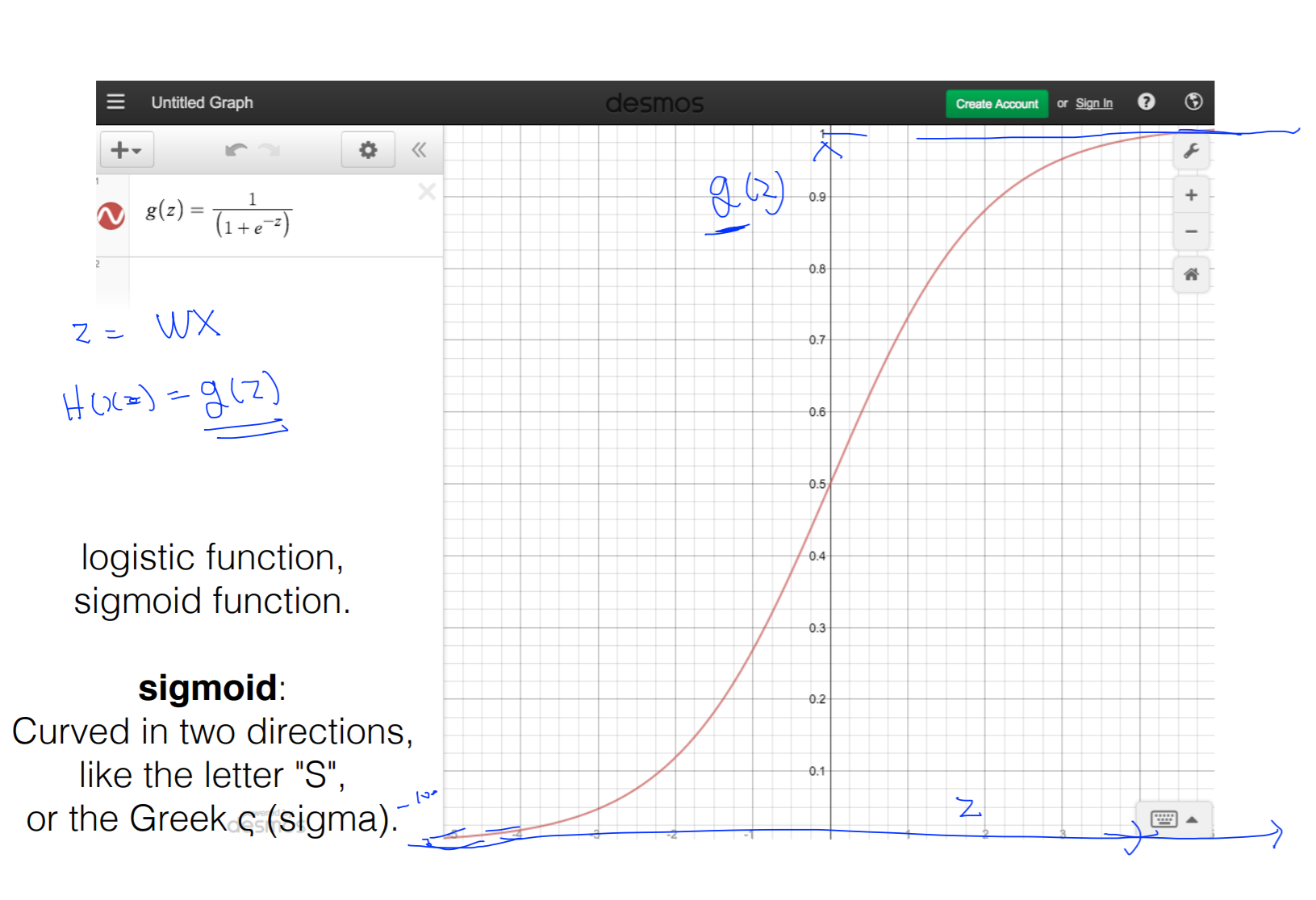
따라서 위의 그림과 같은 것을 찾게 됨
1보다는 크지 않을 것같아 그림을 그리게 되었는데
오른쪽 그림과 같이 나타나게 되었고 이것을 sigmoid라고 부름 또는 logistic function이라고 부름
z가 커지면 g(z)의 함수는 1에 가까워짐
z가 작아지면 g(z)의 함수는 0이 가까워질뿐 0보다는 큰 값을 가짐
그래서 hypothesis의 z를 wx로 두고
H(x) = g(z)로 두면 됨
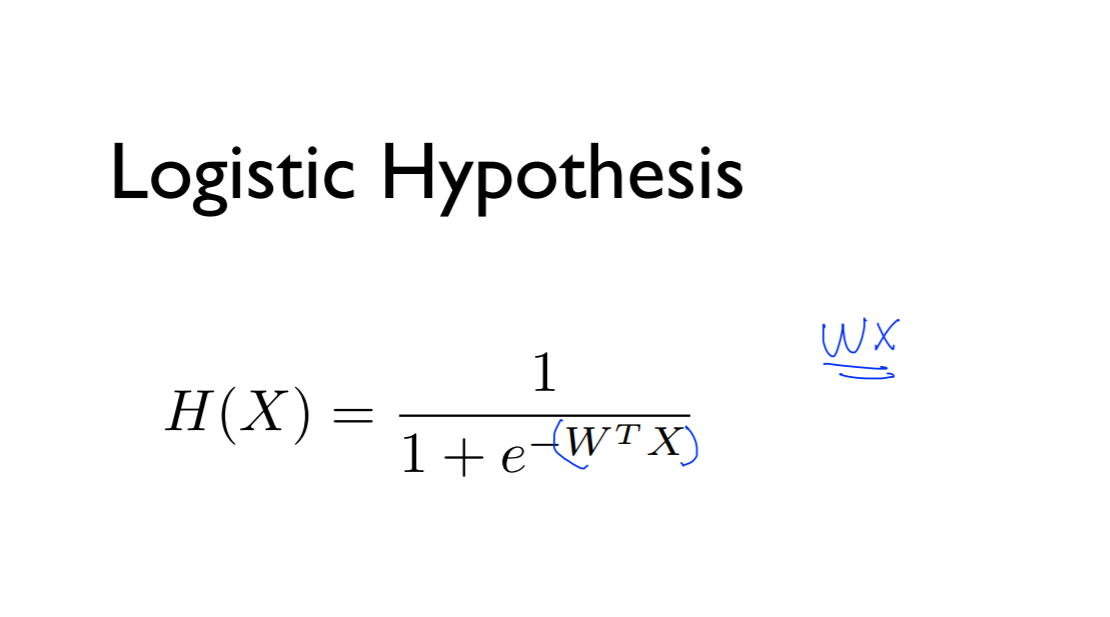
이와 같은 hypothesis를 얻게됨
Next
그 다음은 cost function과 gradient decent에 대해 포스팅함
