[ML] Logistic (regression) classification: Cost function & gradient decent

Cost

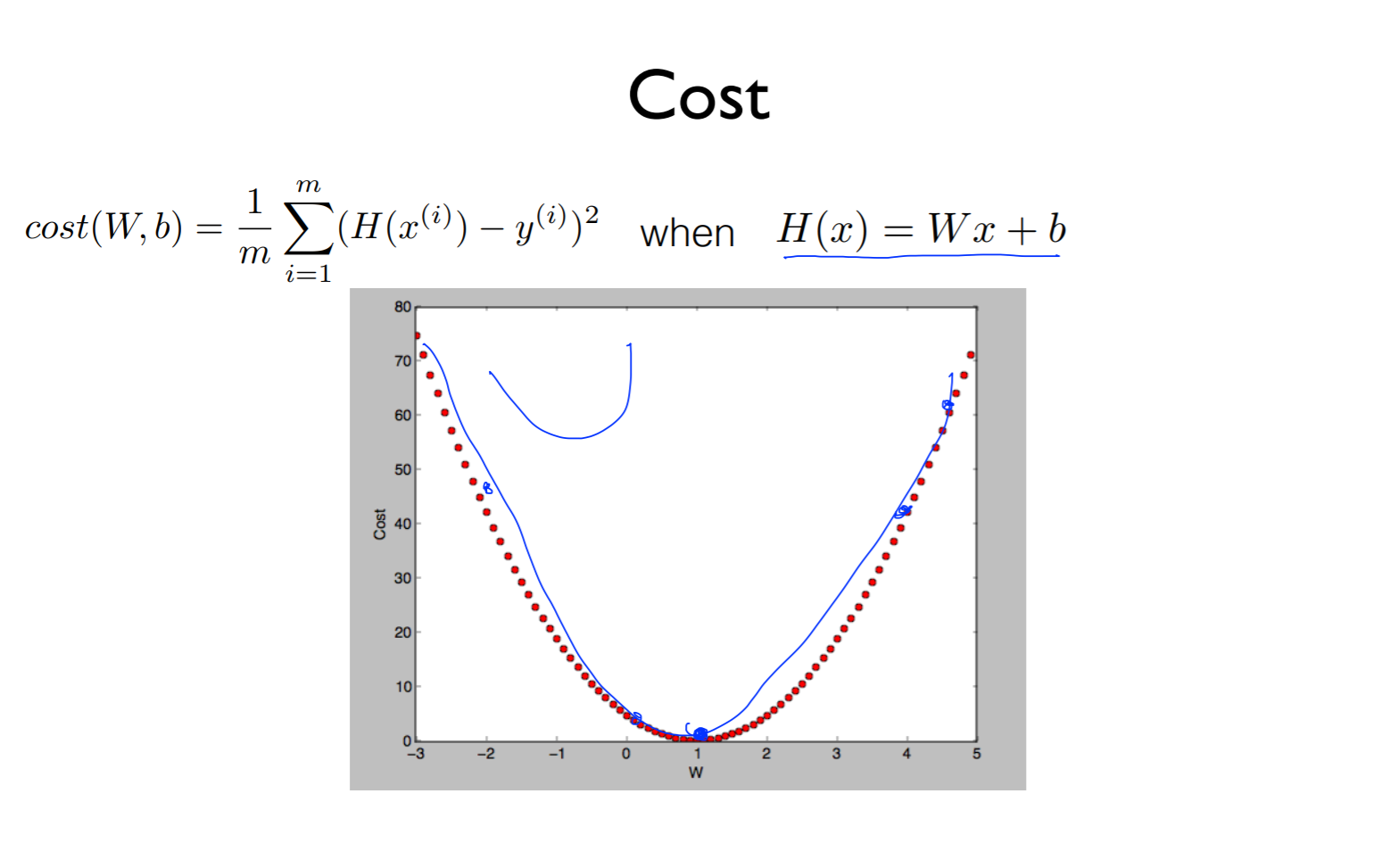
Cost function의 식은 위의 식으로 나타냄
이것을 linear로 hypothsis를 주면 위의 그래프로 그려낼 수 있음

Cost function

가설이 0-1의 값으로 바뀌어 H(X)의 식이 오른쪽 식으로 변경됨

H(x)의 경우 제곱으로 인해 구부러진 그래프가 되고 어느점에서 시작하든 최소값을 도달할 수 있음

H(X)의 경우 식이 linear한 term이 아니기 때문에 shape들이 구부러져 제곱으로 나타냈을 때 양 털같이 그래프가 그려져짐
그리고 어느점에서 시작하든 내려가다가 평평해지는 지점을 만나게 되어서 최소점이 달라질 수 있고 이러한 것을 local medium이라고 함 (그 위치의 주변에 있으니까)

그리고 전체에 대한 최소점을 global medium이라고 함 우리는 global을 찾기 위해 수행하는 것

local에서 찾고 학습을 멈춰버리면 사용할 수가 없기 때문에 cost를 변경해야함 (양털 같은 그래프는 사용할 수 가 없음)

New cost function for logistic

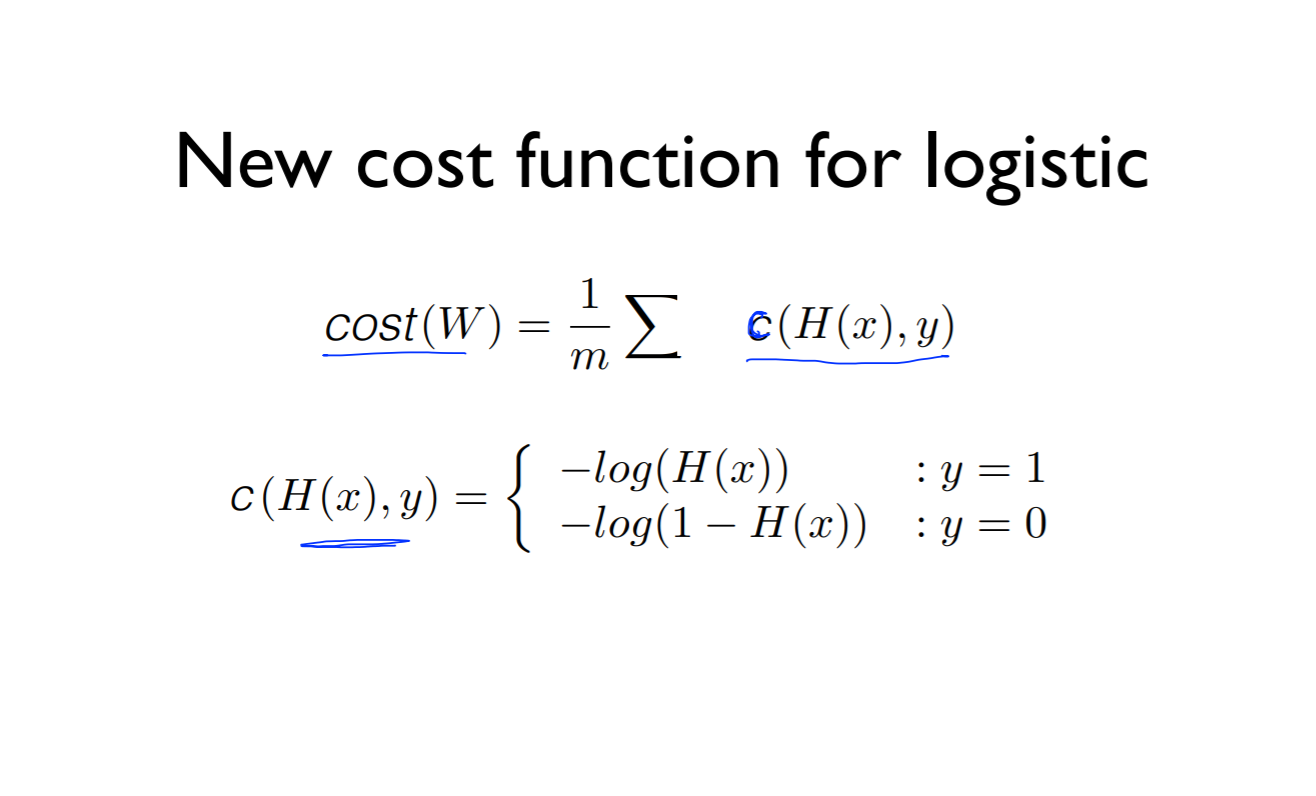
Cost는 어떤 것의 합의 평균, c로 나타내보자
cost를 두 가지로 나눔

understanding cost function

H(x)를 나타내면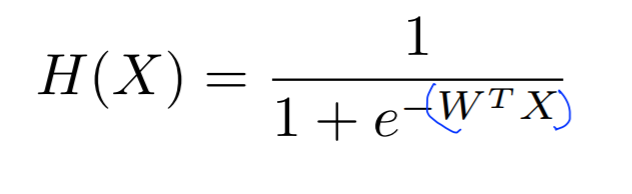

이렇게 되어 있는데 이 e 와 상극이 되는 것은 log

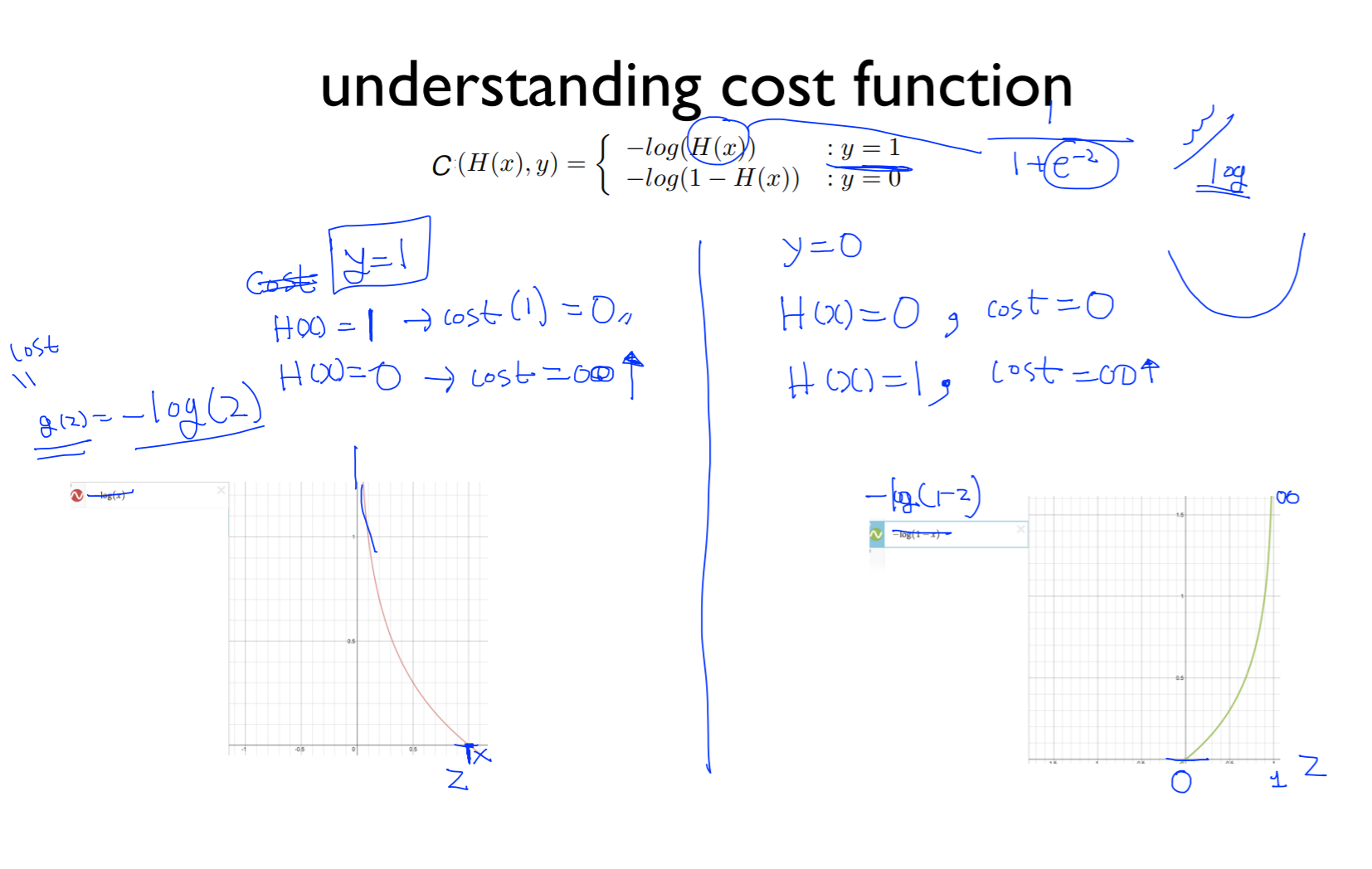
g(z) = -log(2)를 그래프로 그리면 왼쪽 아래 그래프로 그려지고 z값이 0에 가까워지면 함수의 값은 굉장히 커지고 z가 커지면(1에 가까워지면) 0이됨

g(z) = -log(1-z)를 그래프로 그리면 오른쪽 아래 그래프로 그려지고 z 값이(x축) 0이면 0에 가깝고 1이면 무한대에 가까워짐

example

y = 1이고 H(x) = 1(예측한 값)이 맞다고 가정했을 때 cost(1)의 값은 0이 가깝게 됨 (g(z) = -log(2)의 함수로 봤을 때)

H(x) = 0이라고 했을 때 (예측 실패) 이 경우는 cost = 무한대 로 가게 됨

y = 0이고 H(x) = 0인 경우 cost는 0이 됨 실제 레이블과 예측값이 맞았을 때는 cost는 0이 됨
예측 실패로 H(x) = 1인 경우에는 cost가 굉장히 커져 무한대로 가게됨

즉, 두 그래프를 합치게 되면 H(x) = wx + b의 그래프의 cost와 같이 둥근 모양이 됨

cost를 두가지로 나눠서 나타내면 되고, 아래의 식은 두 가지의 식을 합친 식을 나타낸 것

y = 1인 경우에는 cost = -1 * log(H(x)) 가 됨 (위의 식과 같음)
y = 0인 경우에는 cost = -1log(1-H(x)) 가 됨 (위의 식고 같음)

Minimize cost

cost의 기울기를 구하기 위해 미분을 함
현재의 웨이트와 차이로 조금씩 이동

gda library in tensorflow

cost function의 식을 첫번째 코드처럼 나타낼 수 있고,
두번째 코드와 같이 gradient decent algorithm이 tensorflow에 library로 있음