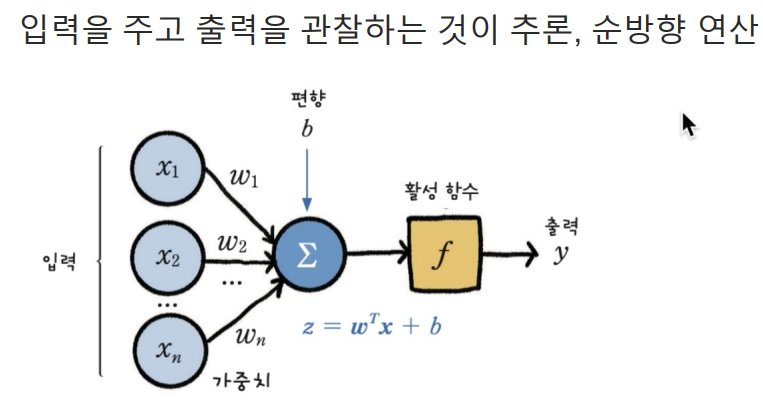
순방향 연산
1. 데이터 준비
import numpy as np
#행렬 X 정의
X = np.array([
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]
])
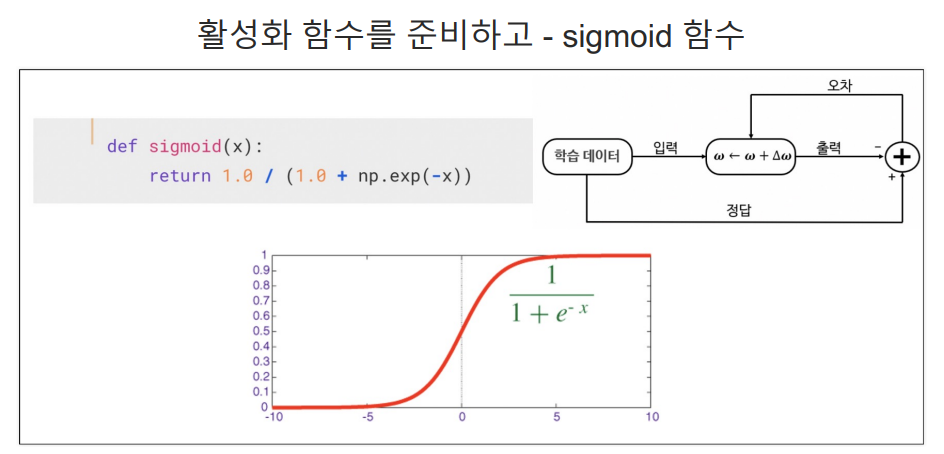
#시그모이드 함수 정의
#시그모이드는 0과 1사이의 값으로 변환, 주로 로지스틱 회귀나 신경망에서 활성화 함수로 사용된다.
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))

#가중치 행렬 W를 초기화 한다.
#1*3 크기의 행렬을 생성하고 각 원소는 0과 1사이의 무작위 값으로 채운다.
W = 2*np.random.random((1,3)) - 1 #2를곱하고 -1을 뺴야한다. 마이너스 랜덤값을 출력하기 위함이다.
W
# 출력 array([[ 0.8177835 , 0.88612231, -0.88451088]])
# X 의 한줄과 위애 W 3개의 값을 곱하는것이다.
# 가중치 행렬 W와 입력 행렬 X의 첫 번째 행을 곱한다.
np.matmul(W, X[0])
#출력 array([-0.88451088])
#0*0.8177835 + 0*0.86612231 + 1 * (-0.8845)
#추론 결과
# 데이터가 4개
#X는 4*3 행렬로, 4개의 다른 입력 벡터 포함
#N은 반복 횟수를 나타내며 여기서는 4로 설정 이는 X의 행 수와 일치
# 결과값이 말도 안되게 틀린 값이 출력된다. 실제 참값은 0011
N = 4
for k in range(N): # 0,1,2,3,
x = X[k, :].T# X 행렬에서 k-번째 행을 선택
v = np.matmul(W, x)
y = sigmoid(v)
print(v)
#결과
[-0.88451088]
[0.00161143]
[-0.06672738]
[0.81939493]
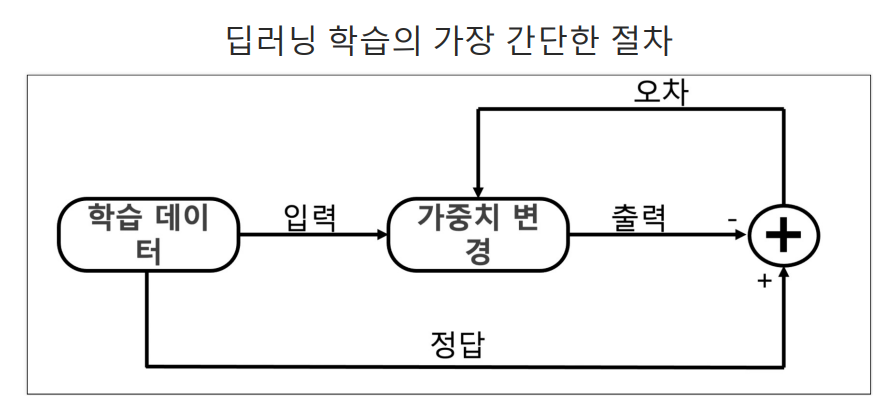
위 결과 오류를 가중치로 정답을 맞추도록 학습 시키기(지도학습)
일단 정답을 주자 - AND
D = np.array([
[0], [0], [1], [1] # 위 실습에서 나온 [-0.88451088][0.00161143][-0.06672738][0.81939493] 값들은 틀린값들이며 각각 0,0,1,1 수치가 정답이다.
])
#일반 모델의 출력 계산하는 함수
#일단 모댈의 출력 계산하는 함수
#이 함수는 신경망 모델 출력을 계산하는 역할을 한다.
#입력 x 와 가중치 W를 받아서 모델 출력 계산
def calc_output(W, x): # 가중치와 X값 을 받는다.
#W; 가중치 행렬 1*3 행렬
#x: 입력 벡터 이 경우 3*1 행렬
v = np.matmul(W, x)
#선형 변환: 가중치 W와 입력 x의 행렬 곱을 계산
y = sigmoid(v)
#비선형 변환: 계산된 선형 변환 결과v를 시그모이드 함수에 통과시켜 비선형 변환을 수행 시그모이드 함수는 결과를 0과 1사이로 스케일링
#하여 활성화 함수로 자주 사용
return y
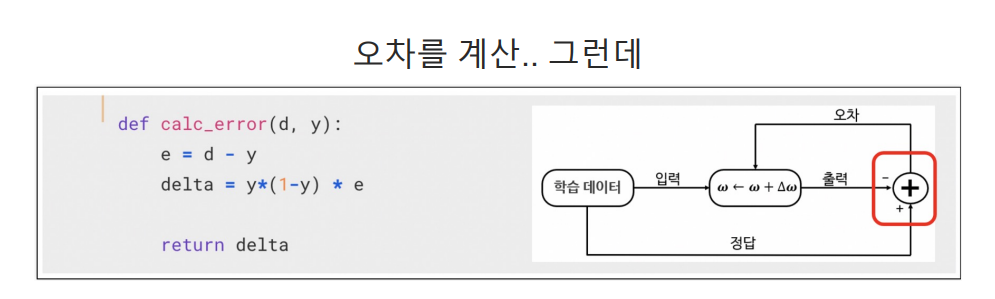
# 오차 계산
#신경망 예측 오차와 그에 따른 오차 기울기를 계산하는 역할
# d: 실제 값 또는 목표 출력 값이며 신경망이 예측해야 하는 정답을 나타낸다.
#y: 신경망의 예측 값. 이 값은 calc_output 함수를 통해 계산된 출력
def calc_error(d,y): # y는 추론값 d는 정답
e = d - y
#오차 계산: 실제 값과 예측 값 사이의 오차를 계산 오차는 신경망의 예측이 얼마나 정확한지를 나타내며 학습 과정에서 이 오차 최소화
delta = y * (1-y) * e #에러와 활성화 함수의 미분값
#오차 기울기 계산: 오차에 대한 가중치의 기울기 계산한다. 이 표현식은 시그모이드 활성화 함수의 미분 사용
#y * (1-y)는 시그모이드 함수의 미분값이며 출력 값에 대한 변화에 따른 오차의 변화율
# 이 값을 오차 e와 곱하면 가중치를 조정하기 위 한 기울기가 된다.
return delta
# 한 epoch에 수행된는 W의 계산
# delta_GD 함수는 경사 하강법(Gradient Descent) 사용하여 한 에폭 동안 신경망의 가중치 W를 업데이트 하는 역할을 한다.
def delta_GD(W, X, D, alpha):
#W: 가중치 행렬 1*3 행렬
#X: 입력 데이터 4*3 행렬
#D: 실제 값 또는 목표 출력 값. 4*1 행렬
#alpha: 학습률 이 값은 가중치 업데이트 크기 조절
for k in range(4):
x = X[k, :].T # X의 K-번째 행 선택
d = D[k]# D의 k-번째 값 선택
y = calc_output(W,x)# 현재 가중치와 입력을 사용하여 모델의 출력 계산
delta = calc_error(d, y)# 실제 값과 모델의 출력 사이의 오차와 그에 따른 오차 기울기 계산
#가중치 업데이트
dW = alpha * delta *x # 가중치 업데이트를 위한 기울기 계산
W = W + dW# 학습률과 계산된 기울기를 사용하여 가중치 업데이트
return W
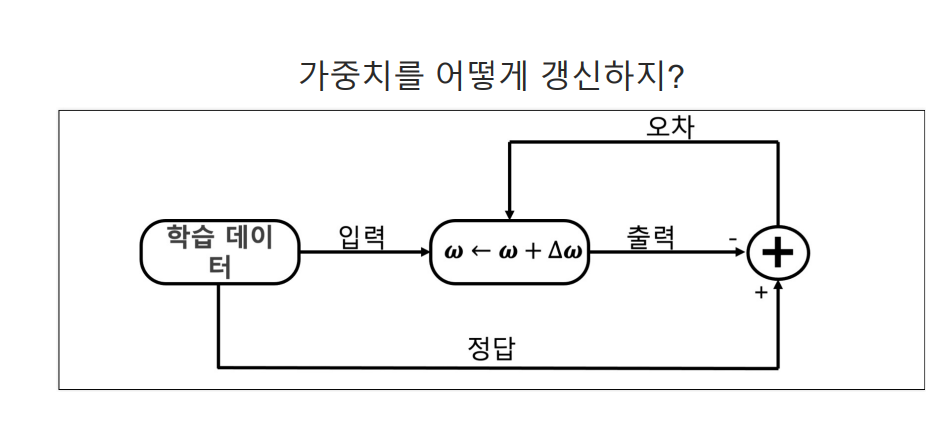
가중치를 랜덤하게 초기화하고 학습 시작
# 경사 하강법 사용하여 가중치 W를 업데이트하기 위한 학습 과정
alpha = 0.9# 매우 큰 학습률 설정
for epoch in range(10000):
W = delta_GD(W, X, D, alpha)
# delta_GD 함수를 호출하고 그 결과로 반환된 업데이트된 가중치 W로 기존의 가중치 대체한다.
# 입력:
# W: 현재 가중치 행렬 (1x3 행렬)
# X: 입력 데이터 (4x3 행렬)
# D: 목표 출력 값 (4x1 행렬)
# alpha: 학습률
# 출력: 업데이트된 가중치 행렬W
print(W)
#
N = 4
for k in range(N):
x = X[k, :].T
v = np.matmul(W, x)
y = sigmoid(v)
print(y)
#출력결과 0,0,1,1 정답이 나왔다.
[0.01018983]
[0.00829532]
[0.99323968]
[0.9916928]
X값
array([[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]])
D값
array([[0],
[0],
[1],
[1]])
오차의 역전파
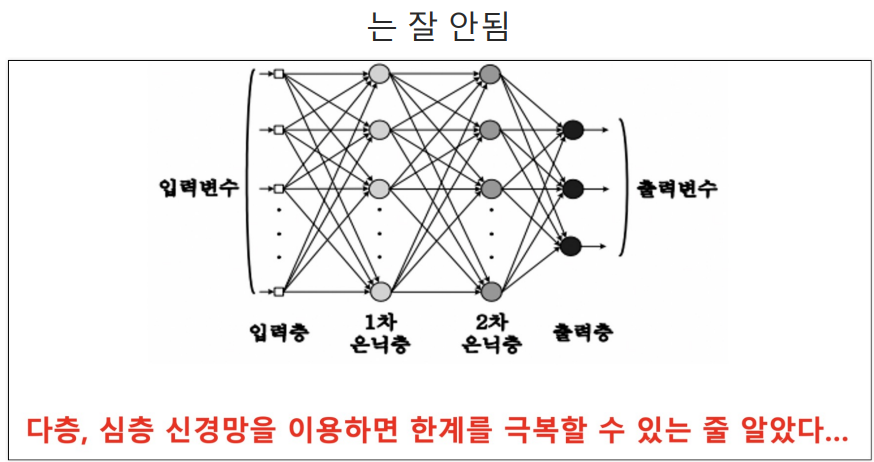
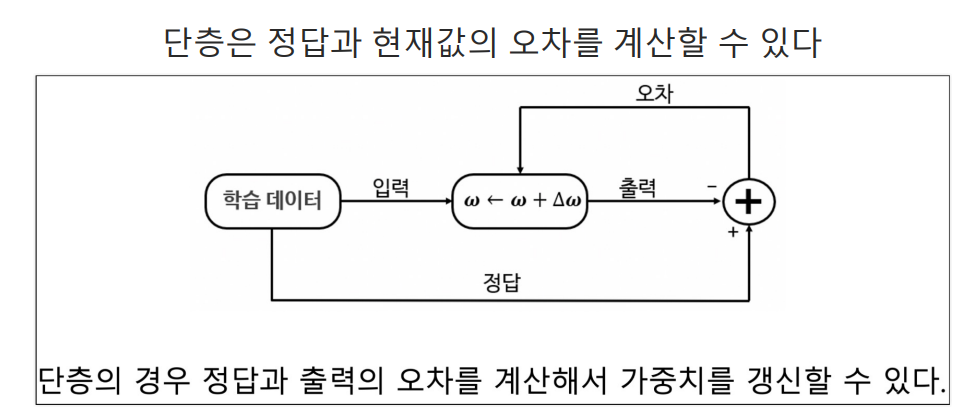
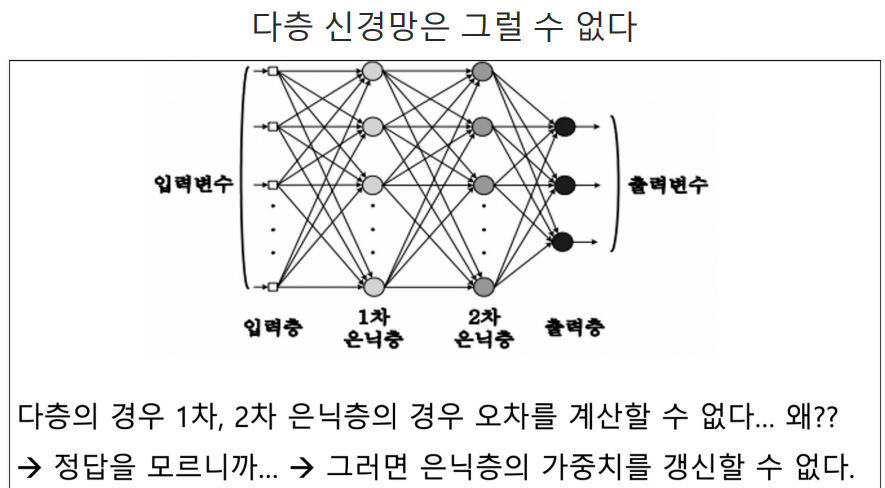

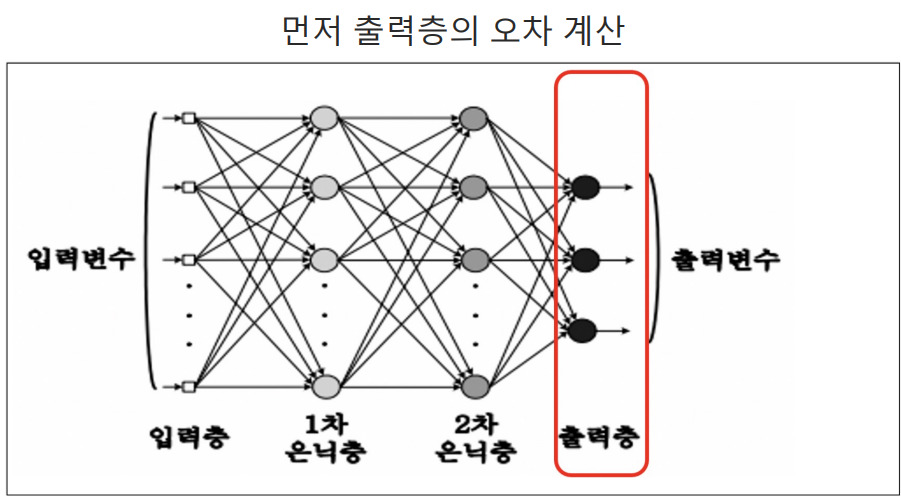
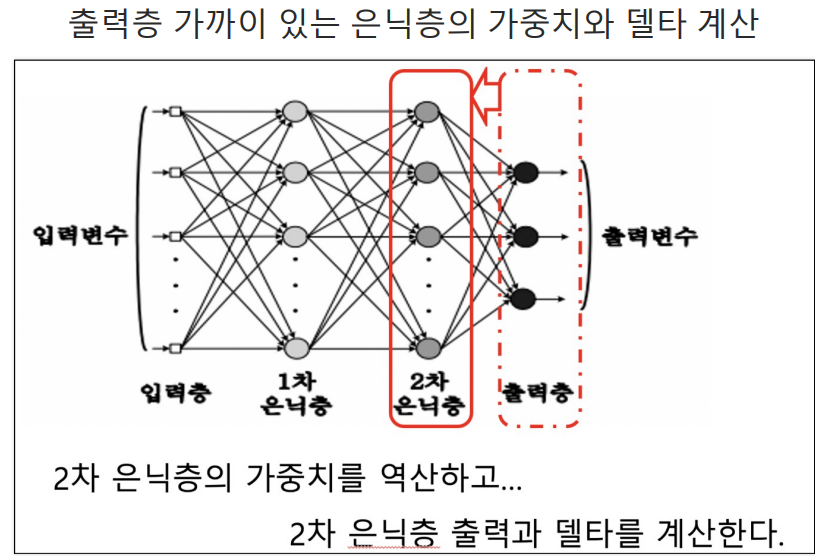
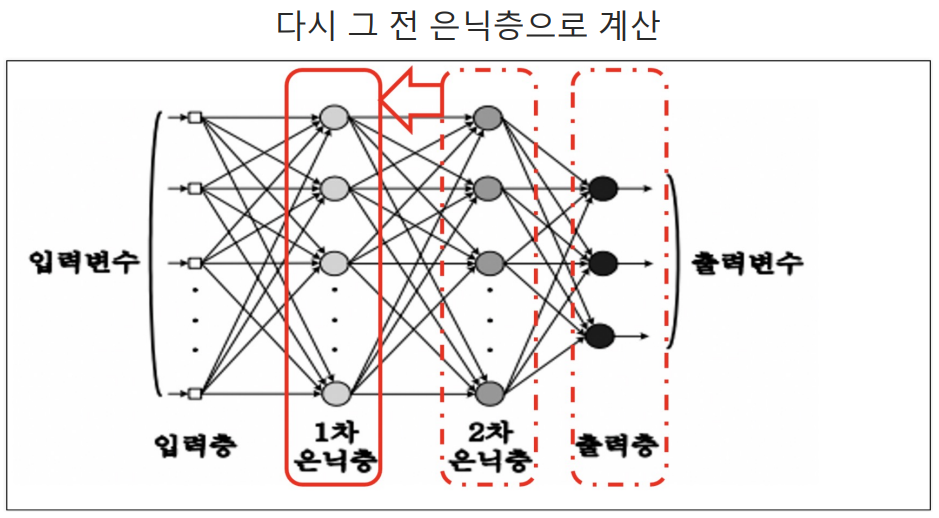
실습
1. 신경망 모델을 위한 초기 설정 수행
import numpy as np
#행렬 X 정의
X = np.array([ #4*3 행렬
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]
])
D = np.array([# 4*1 행렬
[0], [1], [1], [0]
])
W = 2*np.random.random((1,3)) - 1 #2를곱하고 -1을 뺴야한다. 마이너스 랜덤값을 출력하기 위함이다.
# 1*3 행렬
2. 경사 하강법 사용하여 신경망 가중치 W 학습하기
alpha = 0.9 #학습률
for epoch in range(10000):
W = delta_GD(W, X, D, alpha) # 함수를 호출하여 가중치 W 업데이트
3. 가중치 W 사용하여 4 개의 입력 샘플 각각에 대한 신경망의 예측 계산하고 결과 출력
N = 4 #샘플 4개
for k in range(N):
x = X[k, :].T
v = np.matmul(W, x) #가중치 W와 입력 x의 행렬 곱을 계산하여 v에 저장
y = sigmoid(v)
print(y)
#결과
[0.52965337]
[0.5]
[0.47034663]
[0.44090112]
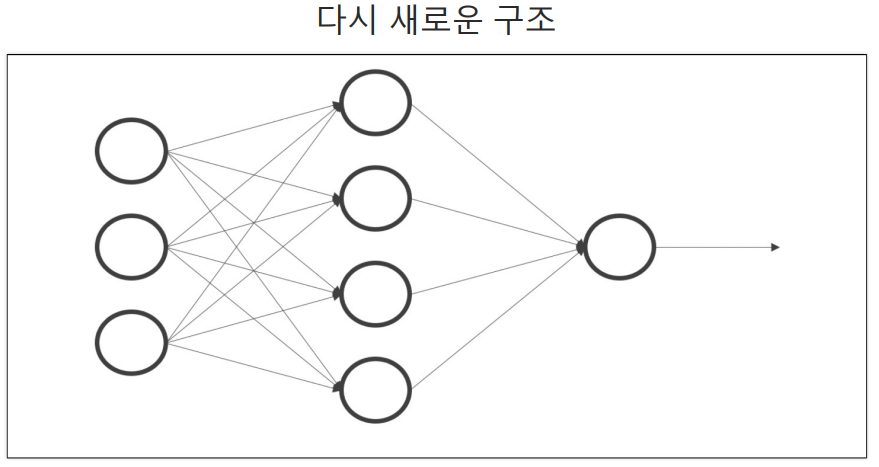
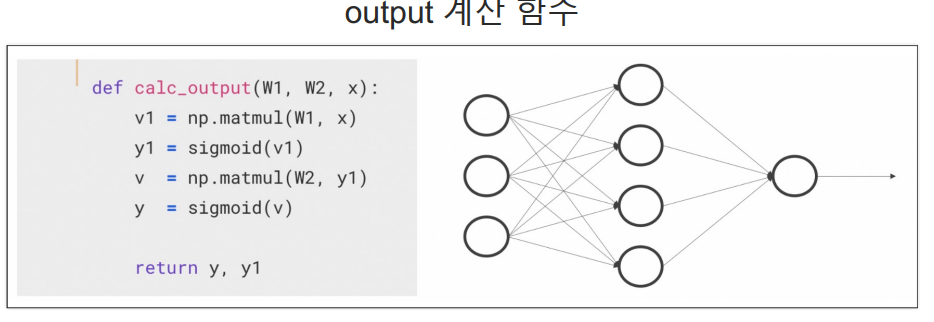
4. 함수 calc_output는 두 층을 가진 신경망 출력을 계산하는 함수
#입력 x, 첫번째 층 가중치 W1 두번쨰 층 가중치 W2를 매개변수로 받는다.
def calc_output(W1, W2, x):
v1 = np.matmul(W1, x)
# 입력 x와 첫 번쨰 층의 가중치 W1의 행렬 곱을 계산하여 v1에 저장
y1 = sigmoid(v1)
#계산된 가중합 v1에 시그모이드 활성화 함수를 적용하여 첫 번쨰 층의 출력 y1 계산
v2 = np.matmul(W2, y1)
#첫번째 층의 출력 y1과 두번쨰 층의 가중치 W2의 행렬 곱을 계산하여 v2에 저장 이 값은 두번쨰 층의 가중합이다.
y = sigmoid(v2)
#계산된 가중합 v에 시그모이드 활성화 함수를 적용하여 신경망의 최종 출력 y를 계산한다.
return y, y1
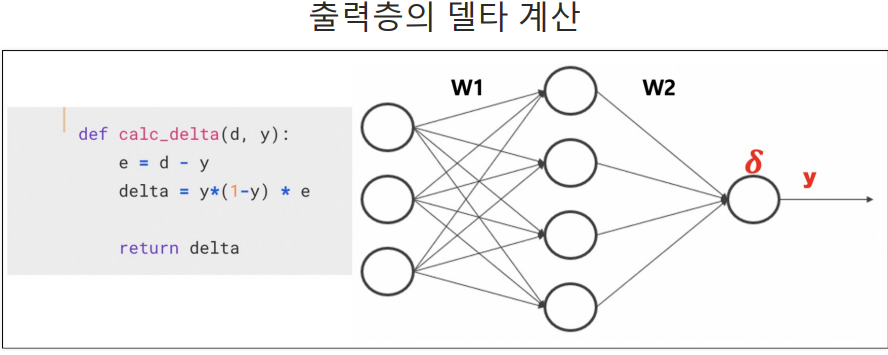
5.신경망 학습 과정에서 오차 역전파를 위해 사용된다.
# 이 함수는 실제값d와 신경망의 예측 값y를 입력으로 받아, 그래디언트를 계산한다.
def calc_delta(d, y):
e = d - y #오차 계산 실제값 d와 예측 값 y사이의 오차 계산 오차는 실제 값과 예측 값의 차이를 나타낸다.
delta = y * (1 - y) * e # 그래디언트 계산: 시그모이드 활성화 함수의 미분과 계산된 오차를 사용하여 그래디언트 계산
#이 그래디언트는 가중치를 어떻게 업데이트해야 할지를 결정하는 데 사용된다.
return delta
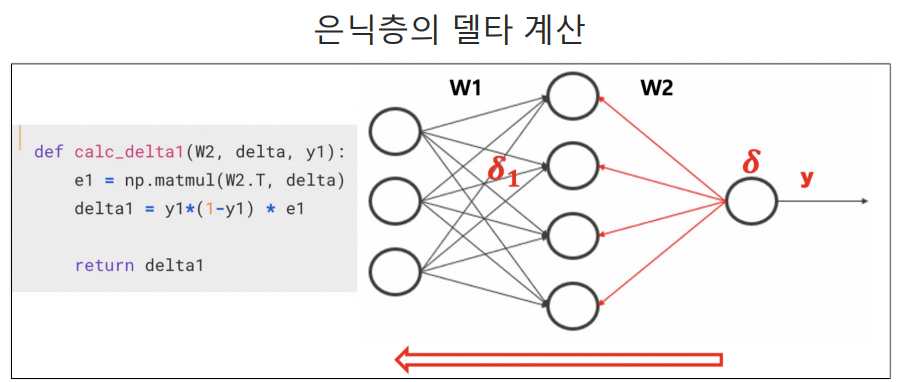
6. calc_delta1는 두층 신경망에서 오차 역전파 과정 일부로 사용된다.
#calc_delta1는 두층 신경망에서 오차 역전파 과정 일부로 사용된다.
# 이 함수는 두번쨰 층의 가중치 W2, 두번 째 층의 오차 그래디언트,
#첫 번쨰 층의 출력y1을 입력으로 받아, 첫번째층의 오차 그래디언트 계산
def calc_delta1(W2, delta, y1):
#오차 역전파
e1 = np.matmul(W2.T, delta)
#두번째 층의 가중치 W2의 전치와 두번째 층의 오차 그래디언트(delta)의 행렬 곱을 계산하여 첫 번째 층의 오차 e1을 계산한다.
#이는 오차를 첫 번째 층으로 역전파하는 과정이다.
#첫번째 층의 오차 그래디언트 계산
delta1 = y1*(1-y1)* e1
#첫번째 층의 출력 y1과 시그모이드 활성화 함수의 미분을 사용하여 첫 번째 층의 오차 그래디언트 계산한다.
return delta1
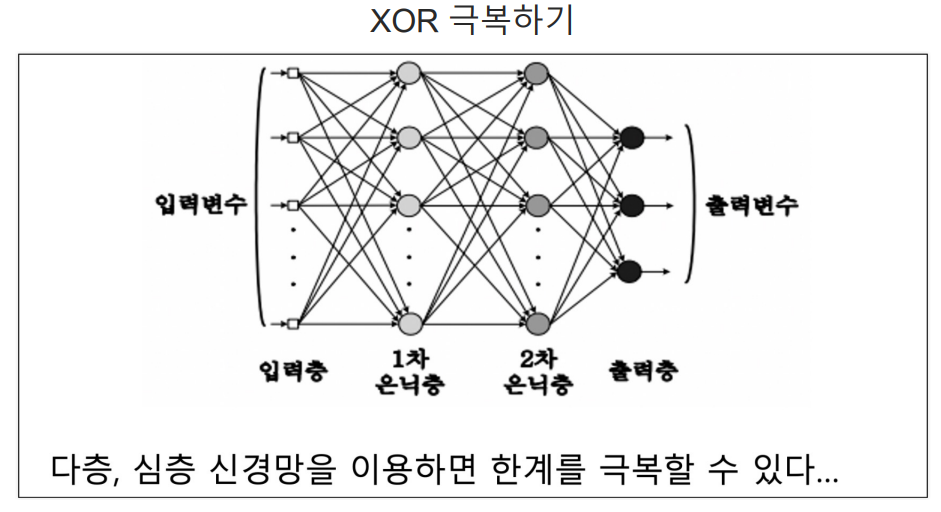
7. XOR 문제를 해결하기 위해 설계된 두 층 신경망에 대한 역전파 알고리즘 구현
def backprop_XOR(W1, W2, X, D, alpha):
# W1: 첫 번째 층의 가중치 행렬
# W2: 두번째 층의 가중치 행렬
# x: 입력 데이터 행렬
# d: 목표 출력 값 행렬
# alpha:학습률 가중치 업데이트 크기 조절
for k in range(4):
x = X[k, :].T #입력 데이터에서 k번쨰 샘플 추출후 전치하여 열 벡터 형태로 만든다.
d = D[k]#해당하는 목표 출력 값 추출
#순방향 전파
y, y1 = calc_output(W1, W2, x)# calc_ouput함수를 사용하여 신경망 출력 계산 y1은 첫번쨰 층의 출력, y는 신경망의 최종 출력
#그래디언트 계산
delta = calc_delta(d, y)#신경망 출력에 대한 오ㅗ차 함수의 그래디언트를 계산
delta1 = calc_delta1(W2, delta, y1)# 첫번쨰 층의 출력에 대한 오차 함수의 그래디언트 계산
#가중치 업데이트
dW1 = (alpha*delta1).reshape(4,1) * x.reshape(1,3) # 첫 번쨰 층의 가중치 업데이트 계산
W1 = W1 + dW1# 첫번쨰 층의 가중치를 업데이트
dW2 = alpha * delta * y1 # 두번쨰 층의 가중치 업데이트 계산
W2 = W2 + dW2# 두번쨰 ㅊ층의 가중치 업데이트
return W1, W2
8. 가독성을 위해 다시 코드사용
X = np.array([ #4*3 행렬
[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]
])
D = np.array([# 4*1 행렬
[0], [1], [1], [0]
])
9.XOR 문제 해결위해 두 층 신경망을 훈련시키는 과정 구현
W1 = 2*np.random.random((4,3)) -1
W2 = 2*np.random.random((1,4)) - 1
alpha = 0.9
for epoch in range(10000):
W1, W2 = backprop_XOR(W1, W2, X, D, alpha)
10. 훈련된 두 층 신경망 모델을 사용하여 입력 X의 각 샘플에 대한 예측 수행하고, 결과 출력하기
N = 4
for k in range(N):
x = X[k, :].T
v1 = np.matmul(W1, x)
y1 = sigmoid(v1)
v = np.matmul(W2, y1)
y = sigmoid(v)
print(y)
#결과
[0.00442485]
[0.99214491]
[0.99409696]
[0.00932415]
크로스엔트로피
- Cross-Entropy: 두 확률 분포 간 차이를 측정하는 데 사용되는 지표이다.
딥러닝에서 분류 문제를 해결할떄 손실 함수로 자주 사용된다. - 크로스 엔트로피 값이 낮을수록 모델의 예측이 실제 레이블에 더 가까워진다는 것을 의미한다.
즉 성능이 좋다는 것을 의미한다. - 신경망 학습에서 크로스 엔트로피 손실을 최소화하기 위해 경사 하강법 이 사용된다.
- 크로스 엔트로피 손실 함수의 그래디언트는 모델의 파라미터에 대해 계산되며, 이를 사용하여 가중치를 업데이트
#크로스 엔트로피 오차 함수 기반으로 역전파 과정에서 오차 그래디언트를 계산한다.
# 크로스 엔트로피는 분류 문제에서 주로 사용되는 오차 함수이다.
#모델 예측이 실제 값에 얼마나 가까운지 측정한다.
def calcDelta_ce(d, y): # d: 실제값, y는 모델의 예측 값
e = d - y# 크로스 엔트로피 미분 결과는 (y-d) 실제 업데이트 과정에서 학습률과 곱해지므로 부호가 반전된다. (y - d)
delta = e
return e
#엔트로피 오차 함수를 사용하는 두 층 신경망에서 오차 역전파 과정의 일부를 구현한다.
def calcDelta1_ce(W2, delta, y1):# 두번째층 가중치W2, 두번째 층의 오차 그래디언트 델타, 첫번째 층의 출력 y1 입력받아
# 첫번째 층의 오차 그래디언트 delta를 계산한다.
e1 = np.matmul(W2.T, delta)
#첫 번째 층의 출력y1에 대한 시그모이드 활성화 함수의 미분 계산 이를 역전파된 e1와 요소별로 곱한다.
# 이결과는 첫 번째 층의 오차 그래디언트 delta1이된다.
delta1 = y1*(1 - y1) * e1
return delta1
# 다시 역전파
#크로스 엔트로피 오차 함수 사용후 두 층 신경망 가중치 업데이트 하는 역전파 알고리즘 구현
def BackpropCE(W1, W2, X, D, alpha):
#X: 입력 데이터
#D: 목표 출력 값 행렬
for k in range(4):
x = X[k, :].T # 현재 샘플을 선택하고 전치하여 열 벡터로 만든다.
d = D[k] # 현재 샘플 목표 출력 값 선택
#순방향 전파:
y, y1 = calc_output(W1, W2, x)# 현재 가중치(W1, W2)와 입력을 사용하여 모델 출력 계산
#역전파 및 그래디언트 계산
delta = calcDelta_ce(d, y) # 출력 오차에 대한 그래디언트 계산
delta1 = calcDelta1_ce(W2, delta, y1)# 첫번째 층의 출력에 대한 오차 그래디언트 계산
#가중치 업데이트
dW1 = (alpha*delta1).reshape(4,1) * x.reshape(1,3) # 첫번째 층의 가중치 업데이트를 위한 그래디언트 계산
W1 = W1 + dW1# 첫 번째 층의 가중치 업데이트
dW2 = alpha * delta * y1 # 두 번째 층의 가중치 업데이트를 위한 그래디언트 곗산
W2 = W2 + dW2# 두번째 층의 가중치 업데이트
return W1, W2
# 학습
W1 = 2*np.random.random((4,3)) -1
W2 = 2*np.random.random((1,4)) - 1
alpha = 0.9
for epoch in range(10000):
W1, W2 = BackpropCE(W1, W2, X, D, alpha)
# 순방향 추론
N = 4
for k in range(N):
x = X[k, :].T
v1 = np.matmul(W1, x)
y1 = sigmoid(v1)
v = np.matmul(W2, y1)
y = sigmoid(v)
print(y) # 0,1,1,0 XOR 출력 성공!
#출력
[3.45859987e-05]
[0.99989487]
[0.99976413]
[0.00035296]