예제1

import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm_notebook



# 벡터 x에 대해 소프트맥스 함수를 계산한다.
def Softmax(x):
    x = np.subtract(x, np.max(x))
    #입력 벡터 x에서 최댓값을 빼서 값을 정규화 한다. 이는 수치적 안정성을 개선하기 위한것
    
    ex = np.exp(x)
    #지수 함수 적용: 정규화된 입력 벡터의 각 요소에 지수 함수를 적용한다.
    
    return ex / np.sum(ex)
    
    
 
 
 
 
 
# 3차원 넘파이 배열 X를 생성하고 특정 패턴으로 채운다. 
# 배열의 차원은 (5,5,5)이다.
# 각 2차원 슬라이스 (X[:,:,i])는 5*5 크기의 행렬로 초기화

X  = np.zeros((5,5,5))

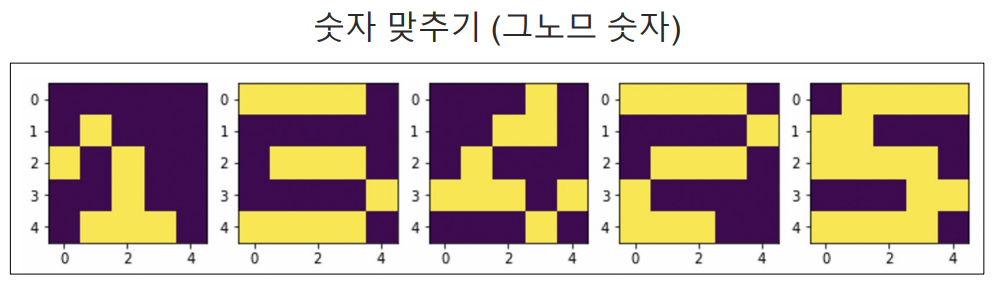
X[:, :, 0] = [[0,1,1,0,0], [0,0,1,0,0], [0,0,1,0,0], [0,0,1,0,0], [0,1,1,1,0]]
X[:, :, 1] = [[1,1,1,1,0], [0,0,0,0,1], [0,1,1,1,0], [1,0,0,0,0], [1,1,1,1,1]]
X[:, :, 2] = [[1,1,1,1,0], [0,0,0,0,1], [0,1,1,1,0], [0,0,0,0,1], [1,1,1,1,0]]
X[:, :, 3] = [[0,0,0,1,0], [0,0,1,1,0], [0,1,0,1,0], [1,1,1,1,1], [0,0,0,1,0]]
X[:, :, 4] = [[1,1,1,1,1], [1,0,0,0,0], [1,1,1,1,0], [0,0,0,0,1], [1,1,1,1,0]]

    
    
 # 시각화
plt.figure(figsize=(12,4))
for n in range(5):
    plt.subplot(1, 5, n+1)
    plt.imshow(X[:,:,n])
plt.show()

---

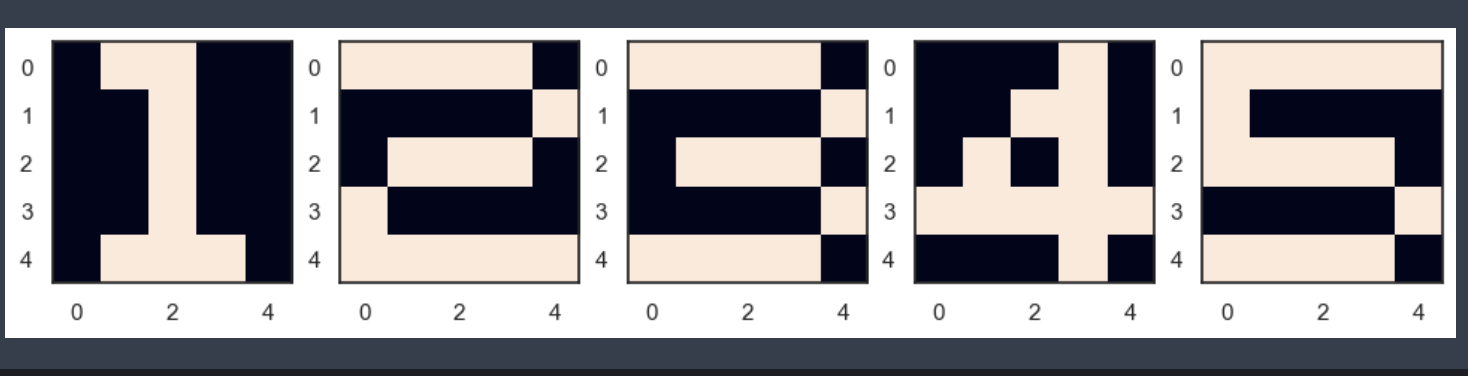
예제2(ReLU 이용한 정방향 계산)

1. ReLU 함수 정의
import numpy as np
from tqdm.notebook import tqdm

# ReLU 함수 정의
def ReLU(x):
    return np.maximum(0, x)

# Softmax 함수 정의
def Softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum(axis=0)





2.ReLU를 이용한 정방향 계산
# 4개의 신경망 출력 계산한다.
# 각 층은 선형 변환후 ReLU 활성화 함수를 적용하고 마지막층은 softmax 활성화 함수를 적용한다.

def calcOutput_ReLU(W1, W2, W3, W4, x): # W1,2,3,4는 각 층의 가중치 행렬이다.
    v1 = np.matmul(W1, x) # v1을 구하기 위해 입력 x에 가중치 W1을 곱한다.
    y1 = ReLU(v1)# y1을 계산하기 위해 v1에 ReLU활성화 함수를 적용한다.
    v2 = np.matmul(W2, y1)# 
    y2 = ReLU(v2)
    v3 = np.matmul(W3, y2)
    y3 = ReLU(v3)
    v = np.matmul(W4, y3)
    y = Softmax(v)#마지막으로 y를 계산하기위해 v에 소프트맥스 활성화 함수를 적용
    
    return y,v1, v2, v3, y1, y2, y3




3. 역전파
# 4층 신경망을 통한 역전파를 수행하여 오차 기울기를 계산한다.
# ReLU 활성화 함수를 사용하기 때문에, 오차 기울기를 계산할 때 해당 뉴런의 입력이 0보다 클 때만 기울기를 전파한다.
# 이 함수는 역전파 과정에서 각 층의 오차 기울기를 계산하여, 가중치를 업데이트 하는 데 사용될 수 있다.

# d: 목표 출력 값(원-핫 인코딩 벡터)
# y: 신경망의 최종 출력(소프트맥스 활성화 함수를 통과한 값)
# W2, W3, W4: 각 층의 가중치 행렬.
# v1, v2, v3: 각 층의 가중합.

def backpropagation_ReLU(d, y, W2, W3, W4, v1, v2, v3):
    e = d - y # 출력 오차 계산
    delta = e# 출력 층의 오차 기울기 delta 계산(가중치 W4 의 전치와 delta의 행렬 곱)
    
    e3 = np.matmul(W4.T, delta)# 세번째 층의 오차 계산(가중치 W4의 전치와 delta의 행렬곱)
    delta3 = (v3 > 0)*e3# 세번째 층의 오차 기울기 delta3 계산(e3와 ReLU 미분 결과의 요소별 곱)
    
    e2 = np.matmul(W3.T, delta3)# 두 번째 층의 오차 e2를 계산한다. (가중치 W3 의 전치와 delta3의 행렬곱)
    delta2  = (v2 > 0) *e2# 두번쨰  층의 오차 기울기 delta2(e2와 ReLU미분 결과의 요소별곱)
    
    e1 = np.matmul(W2.T, delta2)
    delta1 = (v1 > 0)*e1
    
    return delta, delta1, delta2, delta3




4. 가중치 계산
# 함수 기능은 역전파 알고리즘을 사용하여 계산된 오차 기울기를 사용하여 신경망의 가중치를 업데이트 한다.
#이 함수는 신경망 학습 과정에서 각 에포크마다 호출되어 가중치를 업데이트하고, 신경망 성능을 향상시키는 데 사용된다.

# alpha: 학습률, 가중치 업데이트의 크기를 조절합니다.
# delta, delta1, delta2, delta3: 각 층의 오차 기울기.
# y1, y2, y3: 각 층의 출력.
# x: 입력 데이터.
# W1, W2, W3, W4: 각 층의 가중치 행렬.


def calcWs(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4):
    dW4 = alpha * delta * y3.T# dW4는 오차 기울기 delta와 이전 층의 출력 y3의 전치와의 곱에 학습률을 곱한 값
    W4 = W4 + dW4
    
    dW3 = alpha * delta3 * y2.T
    W3 = W3 + dW3
    
    dW2 = alpha * delta2 * y1.T
    W2 = W2 + dW2
    
    dW1 = alpha * delta1 * x.T
    W1 = W1 + dW1
    
    return W1, W2, W3, W4
    
    
    
    
    
 5. 가중치 업데이트
 # 깊은 신경망에 대해 역전파 알고리즘을 사용하여 가중치를 업데이트하는 과정을 구현한다.
#이 신경망은 ReLU 활성화 함수와 Softmax출력층을 사용

#입력 데이터 X
#목표 출력 D
#학습률 alpha

#가중치 행렬 W1, W2, W3, W4
# W1, W2, W3, W4: 각 층의 가중치 행렬.
# X: 입력 데이터 (5x5x5 크기의 3D 배열).
# D: 목표 출력 (5x5 크기의 2D 배열).
# alpha: 학습률, 가중치 업데이트의 크기를 조절합니다.


def DeepReLU(W1, W2, W3, W4, X, D, alpha):
    for k in range(5):
        x = np.reshape(X[:,:,k], (25,1))
        d = D[k, :][:,np.newaxis]
        
        y, v1, v2, v3, y1, y2, y3 = calcOutput_ReLU(W1, W2, W3, W4, x)
        #신경망의 출력y  각층의 가중합(v1,v2,v3) 각 층의 활성화 출력(y1, y2, y3)계산
        
        
        delta, delta1, delta2, delta3 = backpropagation_ReLU(d, y, W2, W3, W4, v1, v2, v3)
        #오차 기울기(delta,delta1,delta2,delta3)계산
        
        W1, W2, W3, W4 = calcWs(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4)
        #가중치 행렬(W1,W2,W3,W4)행렬을 업데이트한다.
        
    return W1, W2, W3, W4
    
    
    
    
    
    
 6. 학습하기
# 가중치 랜덤하게 뽑은후 학습 시작하기
# 4층 신경망을 학습시키기 위한 코드 
#각 층에는 여러 개의 뉴런이 있고, 각 뉴런은 가중치를 가지고 있다.
#학습을 위해 무작위로 초기화된 가중치로 시작하여, 예측 오차를 줄이기 위해 반복적으로 가중치 조정한다.

import tqdm
W1 = 2 * np.random.random((20,25)) - 1 # 가중치 크기 (20,25)이며  -1과 1 사이의 균등 분포에서 무작위로 선택된 값으로 초기화
W2 = 2 * np.random.random((20,20)) - 1
W3 = 2 * np.random.random((20,20)) -1
W4 = 2 * np.random.random((5,20)) - 1

alpha = 0.01
for epoch in tqdm.tqdm_notebook(range(10000)):
    W1, W2, W3, W4 = DeepReLU(W1, W2, W3, W4, X, D, alpha)
    #입력 데이터 X와 목표 출력 D를 사용하여 학습을 진항하게 된다. 
    #1만번의 에포크가 끝나면, 신경망의 가중치 W1, W2, W3, W4는 훈련 데이터에 더 잘 맞도록 조정
    
    
    
    
    
 7. 훈련 데이터 검증
 def verify_algorithm(x, W1, W2, W3, W4):
    v1 = np.matmul(W1, x)
    y1 = ReLU(v1)
    
    v2 = np.matmul(W2, y1)
    y2 = ReLU(v2)
    
    v3 = np.matmul(W3, y2)
    y3 = ReLU(v3)
    
    v = np.matmul(W4, y3)
    y = Softmax(v)
    
    return y
  
  
  
  
  
  
  
  8. 결과

N = 5
for k in range(N):
    x = np.reshape(X[:,:,k], (25,1))
    y = verify_algorithm(x, W1, W2, W3, W4)
    
    print("Y = {}:".format(k+1))
    print(np.argmax(y, axis=0) + 1)
    print(y)
    print('--------')
#결과
Y = 1:
[1]
[[9.99961397e-01]
 [1.39639399e-08]
 [2.81797726e-05]
 [7.19283051e-10]
 [1.04086870e-05]]
--------
Y = 2:
[2]
[[6.85400057e-06]
 [9.99975499e-01]
 [9.74599451e-06]
 [7.90080899e-06]
 [5.09081220e-12]]
--------
Y = 3:
[3]
[[1.90029615e-05]
 [7.06403933e-06]
 [9.99942559e-01]
 [3.13728426e-05]
 [1.40261217e-09]]
--------
Y = 4:
[4]
[[3.94499217e-08]
 [1.86645168e-05]
 [1.98764111e-05]
 [9.99961411e-01]
 [8.48558374e-09]]
--------