$A \bold x=\bold b$

$A\bold x= \bold b$의 의미

$m\times n$ 행렬 $A$에 대해서 $A\bold x$는 아래와 같이 표현할 수 있다.

• $n$개의 열벡터($\bold{a_i}$)로 이루어진 행렬 $A$와 $n$개의 미지수로 이루어진 벡터 $\bold x$의 곱
• 각 열벡터($\bold{a_i}$)와 벡터 $\bold x$의 요소들($x_i$)의 선형결합 → $\bold b$
  = $A$의 column들의 liner combination이다.
  

따라서 $A\bold x=\bold b$ 방정식은 벡터 $\bold b$가 $A$의 Column space 안에 들어있다면 해를 가진다. (if and only if)

Some Terminology : 용어

elimination이 진행된 행렬 $A$에 대해, $A\bold x = 0$ 에서

• Pivot column: 행렬 $A$에서 pivot을 가지는 column
• Free column: 행렬 $A$에서 pivot을 가지지 않는 column
• Pivot variable: 벡터 $\bold x$에서 행렬 $A$의 pivot column에 곱해지는 변수 (요소)
• Free variable: 벡터 $\bold x$에서 행렬 $A$의 free column에 곱해지는 변수 (요소)

예시 : 아래 행렬에서 pivot/free column과 pivot/free variable은?

• pivot column : $[1\ \ 0 \ \ 0]^T$, $[2\ \ 1 \ \ 0]^T$ (pivot : $1, 1$)
  
• free column : $[1\ \ 4 \ \ 0]^T$, $[0\ \ -1 \ \ 0]^T$
• pivot variable : $x_1, x_2$
• free variable : $x_3, x_4$

NullSpace 구하기 : special solution

method 1

각각의 pivot variable을 free variable를 이용해서 표현하고 벡터 $\bold x$에 대입한다.

1. $A\bold x = \bold 0$ 꼴로 행렬을 표현한다.

2. $A$에 대하여 Gauss Elimination을 진행한다.

3. 이후 $\bold x$의 pivot variable을 free variable로 표현한다.

   → fv의 선형결합으로 표현된 pc를 각각의 표현으로 분리한다.

4. 그렇게 free variable로 표현된 변수들을 벡터 $\bold x$에 대입한다.

5. 벡터 $\bold x$를 각각의 free variable과 벡터*의 linear combination 으로 표현한다. ⇒ solution to $A\bold x= \bold 0$, $N(A)$

   이때, 각각의 벡터를 special solution이라고 부른다.

• 표현 예시

  1. variable에 대해 다음 두 방정식이 주어졌다. (fv : $x_2, x_4, x_5$ 일 때)

     • $x_1 = -2x_2 + 2x_5$
     • $x_3 = -x_4-2x_5$

  2. 식을 활용하여 벡터 $\bold x$에 대입한다.

     $\bold x = \begin{bmatrix} x_1\\x_2\\x_3\\x_4\\x_5 \end{bmatrix} = \begin{bmatrix} -2x_2 + 2x_5\\x_2\\-x_4-2x_5\\x_4\\x_5 \end{bmatrix}$

  3. 각각의 free variable에 대한 선형결합으로 표현한다.

     $\bold x = x_2 \begin{bmatrix} -2\\1\\0\\0\\0 \end{bmatrix}+x_4 \begin{bmatrix} 0\\0\\-1\\1\\0 \end{bmatrix}+x_5 \begin{bmatrix} 2\\0\\-2\\0\\1 \end{bmatrix},\ \ \ x_2,x_4,x_5\in \mathbb R$

method 2

free variable중 하나의 변수에는 1을 대입하고 나머지에는 0을 대입하는 과정을 반복한다.

1. $A\bold x = \bold 0$ 꼴로 행렬을 표현한다.

2. $A$에 대하여 Gauss Elimination을 진행한다.

3. 여러개의 free variable중 하나를 1로 하고 다른 free variale들은 0을 대입하여 표현한다.

4. 3번 과정을 거쳐 이제 pivot variable의 값만 알아내면 되는 벡터 $\bold x$에 대해 $A\bold x = \bold 0$ 을 풀어 벡터: special solution를 구한다.

5. 각각의 모든 free variable에 해당 과정을 반복해서(1인 variable을 변경해줌) 적용하여 모든 special solution들을 구한다.

6. 이렇게 구한 special colution들의 linear combination ⇒ solution to $A\bold x= \bold 0$, $N(A)$

   
   

• 표현 예시
  fv : $x_2, x_4, x_5$ 일 때
  1. variable에 대해 다음 두 방정식이 주어졌다. (fv : $x_2, x_4, x_5$ 일 때)
     • $x_1 = -2x_2 + 2x_5$
     • $x_3 = -x_4-2x_5$
  2. 각 case별 Special solution
     • $x_2 = 1, x_4 = 0, x_5 = 0$
       $\bold x = \begin{bmatrix} -2x_2 + 2x_5\\1\\-x_4-2x_5\\0\\0 \end{bmatrix} = \begin{bmatrix} -2 \\1\\0\\0\\0 \end{bmatrix}$
     • $x_2 = 0, x_4 = 1, x_5 = 0$
       $\bold x = \begin{bmatrix} -2x_2 + 2x_5\\0\\-x_4-2x_5\\1\\0 \end{bmatrix} = \begin{bmatrix} 0 \\0\\-1\\1\\0 \end{bmatrix}$
     • $x_2 = 0, x_4 = 0, x_5 = 1$
       $\bold x = \begin{bmatrix} -2x_2 + 2x_5\\0\\-x_4-2x_5\\0\\1 \end{bmatrix} = \begin{bmatrix} 2 \\0\\-2\\0\\1 \end{bmatrix}$
  3. Special solution들의 linear combination
     $\bold x = x_2 \begin{bmatrix} -2\\1\\0\\0\\0 \end{bmatrix}+x_4 \begin{bmatrix} 0\\0\\-1\\1\\0 \end{bmatrix}+x_5 \begin{bmatrix} 2\\0\\-2\\0\\1 \end{bmatrix},\ \ \ x_2,x_4,x_5\in \mathbb R$

special solution?

• NullSpace를 이루는 vector
• special solution은 free variable(=free column)의 개수와 동일하다.
• free variable의 개수 = 전체 column의 갯수 - pivot의 개수 ($n-r$)

Complete Solution

Theorem

벡터 $\bold w$가 $A\bold x= \bold b$의 임의의 solution이라고 가정하자. Then,

• $A\bold x= \bold b$ 의 solution이 $\bold y$이면 $\bold y = \bold w+\bold z$ 이다. ($\bold z \in N(A)$)
  pf)
  1. $\text{if }\ A\bold y = \bold b$ 이라면,
     $A\bold y - A\bold w = \bold b - \bold b =0\\\ \\A(\bold y - \bold w) = 0$
  2. 따라서 벡터 $\bold y - \bold w$는 NullSpace에 속하는 vector이다.
     $\bold y - \bold w \in N(A)$
  3. 벡터 $\bold z$를 NullSpace에 속하는 또다른 vector라고 하면, linear combination 성질에 의해
     $\bold y-\bold w = \bold z\ \ (\bold z \in N(A))\\\ \\ \bold y = \bold w + \bold z$
• ↔  $\bold y = \bold w+\bold z$ ($\bold z \in N(A)$) 이면 $\bold y$는 $A\bold x= \bold b$의 solution이다.
  pf)
  1. $\text{if }\ \bold y = \bold w+\bold z$ 이라면,
     $A\bold y = A(\bold w + \bold z)= A\bold w + A\bold z$
  2. 이때, 처음 Theorem의 가정에 따라 $A\bold w = \bold b$이고 $\bold z$는 NullSpace에 속하는 벡터이므로 $A\bold z = \bold 0$
     $\bold b + \bold 0 = \bold b$
  3. 따라서 $\bold y$는 $A\bold x= \bold b$의 solution이다.
     $A\bold y = \bold b$

$\bold y = \bold w + \bold z$ 를 이용하여 모든 solution을 표현할 수 있다.

→ 즉, NullSpace를 구하여 그 벡터 ($\bold z \in N(A)$)에 임의의 solution $\bold w$를 더하면 complete solution을 표현할 수 있다.

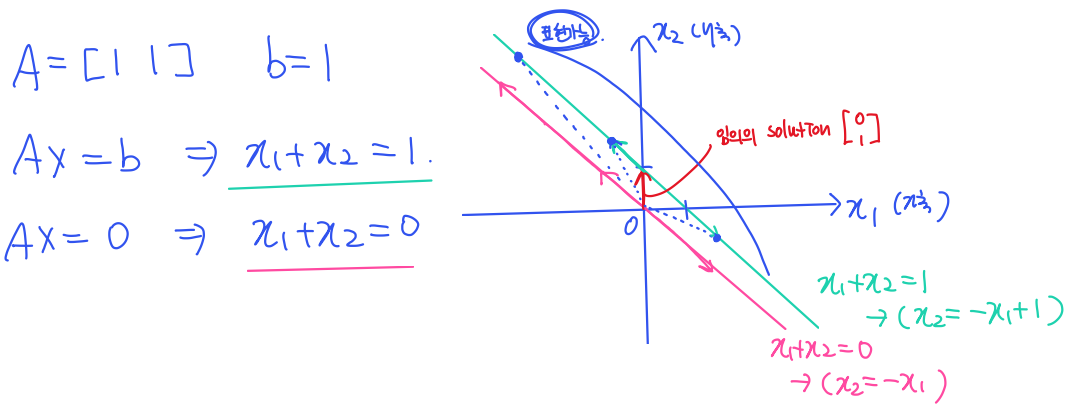
기하학적 의미

• 임의의 solution과 NullSpace의 vector(special solution)을 더한 vector의 종점은 여전히 $A\bold x = \bold b$ 안에 들어있다.
• 따라서 NullSpace의 어떤 solution과 임의의 solution의 합으로 $A\bold x = \bold b$의 모든 solution을 표현할 수 있다.

과정

1. $A\bold x = \bold b$의 아무 solution을 찾는다. $(=x_p)$

   • 임의의 어떤 solution이던간에 관계없음
   • 따라서 가장 쉽게 solution을 찾을 수 있도록 fv를 0으로 가정하고 $A\bold x = \bold b$를 풀어서 particular solution을 구한다.

2. $A\bold x = \bold 0$의 solution을 찾는다. → Null Space를 찾는다. $(N(A) = x_n)$

3. $x_p + x_n$이 $A\bold x = \bold b$의 complete solution이 된다.

   (NullSpace의 모든 vector에 대해 진행하여 새로운 벡터 공간을 정의함)

완전해(complete solution)은 특수해들의 선형조합이다.

• 특수헤?
  • $A\bold x = \bold 0$ 의 해 (=Special solution) : NullSpace의 벡터
  • $A\bold x = \bold b$의 임의의 solution (=particular solution)