POSS:Position Specialist Generates Better Draft for Speculative Decoding

Hyunjoon Jeong·2025년 11월 9일

목록 보기

11/13

오늘 리뷰할 논문은 POSS라는 논문이다. 이 논문은 사내에서 speculative decoding 스터디를 할 때 소개 받은 것인데, 내 뒷자리에 앉아 있는 분이 이 논문에서 많은 영감을 받은 것 같았다. 그 분이랑 아이디어 얘기를 하면서 이 논문을 한 번 읽어 봐야겠다는 생각이 들었다. (사실 그 분의 아이디어를 이해하기 조금 어려운 부분이 있어서, 리뷰를 해야겠다는 생각이 들었다.)

https://arxiv.org/abs/2506.03566

EAGLE-2와 HASS의 문제점

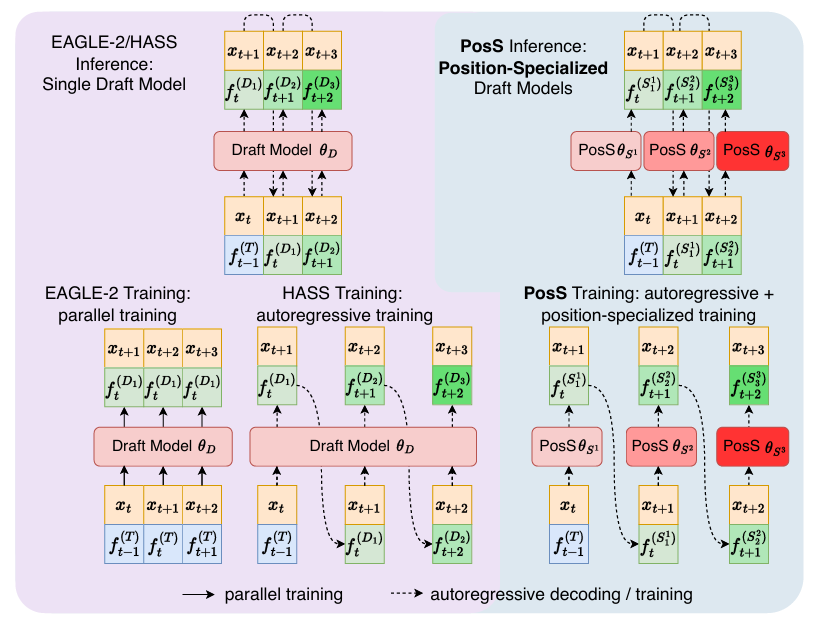
예전에는 draft 모델와 target 모델을 따로 사용하는 speculative decoding이 유행이였지만, Medusa나 Eagle이 등장하면서 target 모델의 hidden state를 draft의 입력값으로 사용하는 패러다임이 등장하면서 1-layer transformer나 특수한 LM head를 draft 대신 사용하는 방식이 각광을 받고 있다. 실제로도 내가 speculative decoding 실험을 할 때, 적절한 draft 모델을 찾는 것이 어렵기도 하고, GPU 메모리 문제도 있어서 이러한 방식이 좋은 해결책으로 떠오르고 있다. 그 중, EAGLE이나 Medusa는 vLLM V1 버전의 speculative decoding의 옵션으로 사용이 될 만큼 좋은 성능까지 보여준다.

하지만 어느 논문이든 문제점이 없지는 않다. EAGLE의 경우, training과 inference 사이에 일치하지 않는 문제가 존재한다. 학습 시에는 target 모델의 정답 feature를 이용해 토큰을 예측한다. 하지만 실제 inference 환경에서는 이전 위치의 정답 feature를 사용 할 수 없고, draft가 생성한 feature에 의존하게 된다. 이로 인해 점점 오차가 누적이 되면서 후반부의 예측에서 품질이 떨어지는 문제가 있다.

HASS라는 논문은 이를 해결하기 위해서 draft 모델이 이전 draft 단계의 feature를 사용해서 다음 토큰을 예측하도록 학습 시킨다. 하지만 이러한 방식은 단일 draft 모델이 draft sequence 내 여러 위치의 토큰을 동시에 예측해야 하는 문제점이 있기 때문에 여전히 뒤쪽 토큰 예측은 부정확한 문제가 있다.

Position Specialist (POSS) Method

POSS는 뒤쪽 토큰이 feature 오차가 누적 되기 때문에 예측이 어렵다는 점을 위치마다 특화 된 draft 모델을 따로 두는 방식으로 개선하고자 했다. 기존처럼 draft를 하나만 사용 하는 방식 대신, 여러 개의 위치별 특화 draft layer를 이용한다.

Position-wise Acceptance Rate (pos-acc)

앞서 언급하였듯, 이전의 EAGLE-2와 HASS는 하나의 draft layer가 여러 위치의 토큰을 잘 생성 할 수 있다는 일반화 능력에 의존한다. POSS는 이에 대한 일반화의 한계를 보여주기 위해 position-wise acceptance rate을 다음과 같이 정의하였다. 이는 이전 위치의 토큰이 accept 되었다는 조건 하에, 해당 위치의 토큰이 accept 될 확률을 의미한다.

pos-acc_i = P(A_i|A_{i-1}) = \frac{P(A_{i-1}\cap A_i)}{P(A_{i-1})} = \frac{P(A_i)}{P(A_{i-1})}\ ,\ i>1

위 식에서 $A_i$ 는 어떤 위치 $i$ 의 토큰이 검증 단계에서 승인된 사건을 의미한다. target 모델의 검증은 sequential dependency를 가지기 때문에, 만약 토큰 $x_i$ 가 accept이 되었다는 말은, 그 이전의 토큰인 $x_0$ 부터 $x_{i-1}$ 까지도 모두 accept이 되었다는 것을 의미한다. 그렇기 때문에 $A_i \subset A_{i-1}$ 가 성립한다.

pos-acc가 높을수록, 각 drafting 단계에서 더 긴 acceptance length를 얻을 수 있게 된다. 만약 draft sequence의 길이를 $L$ 이라고 할 때, 앞에서부터 $k$ 번째 위치까지의 모든 토큰이 accept 될 확률을 다음과 같이 표현 할 수 있다.

P(A_1 \cap A_2 \cap ...\ \cap A_k) = \begin{cases} P(A_1),\ k=1 \\ P(A_1) \prod_{i=2}^k pos-acc_i\ ,\ k>1 \end{cases}

위 식을 보면, 전체 acceptance length는 각 위치별 pos-acc의 곱에 의해 결정되기 때문에, 어느 한 위치라도 pos-acc 값이 낮아지면 전체 성능이 급격하게 떨어지게 된다. EAGLE-2와 HASS의 경우, 후반부 토큰으로 갈 수록 예측 오차가 누적 되고 불확실성이 증가하기 때문에 pos-acc가 감소하게 된다.

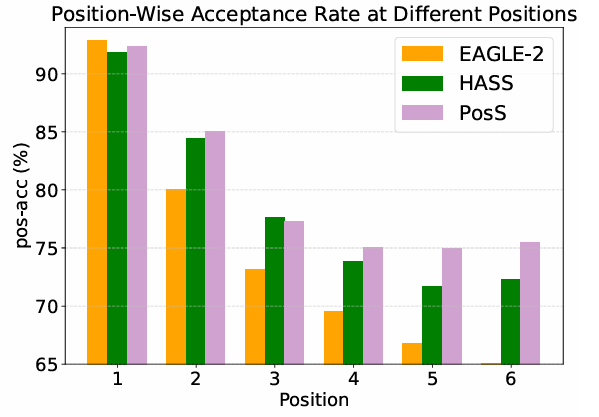
위 그래프는 EAGLE-2와 HASS의 실제 pos-acc 측정 결과이다. EAGLE-2의 경우, $k=1$ 이후 부터 pos-acc가 급격하게 떨어지는데, 이는 EAGLE-2의 draft 모델이 오로지 다음 한 토큰만 예측하도록 학습이 되어 있기 때문이다. HASS의 경우, EAGLE-2보다는 상대적으로 높은 pos-acc를 가지는데, 이는 여러 위치를 동시에 학습했기 때문이다. 그러나 하나의 draft 모델이 여러 위치를 동시에 커버해야 하기 때문에, $k=1$ 에서도 1%의 pos-acc 감소가 발생하고, 이는 pos-acc가 누적곱으로 연산이 되기 때문에 작은 값의 감소도 전체 acceptance length에 치명적인 영향이 가게 된다.

Position Specialist를 이용한 pos-acc 향상

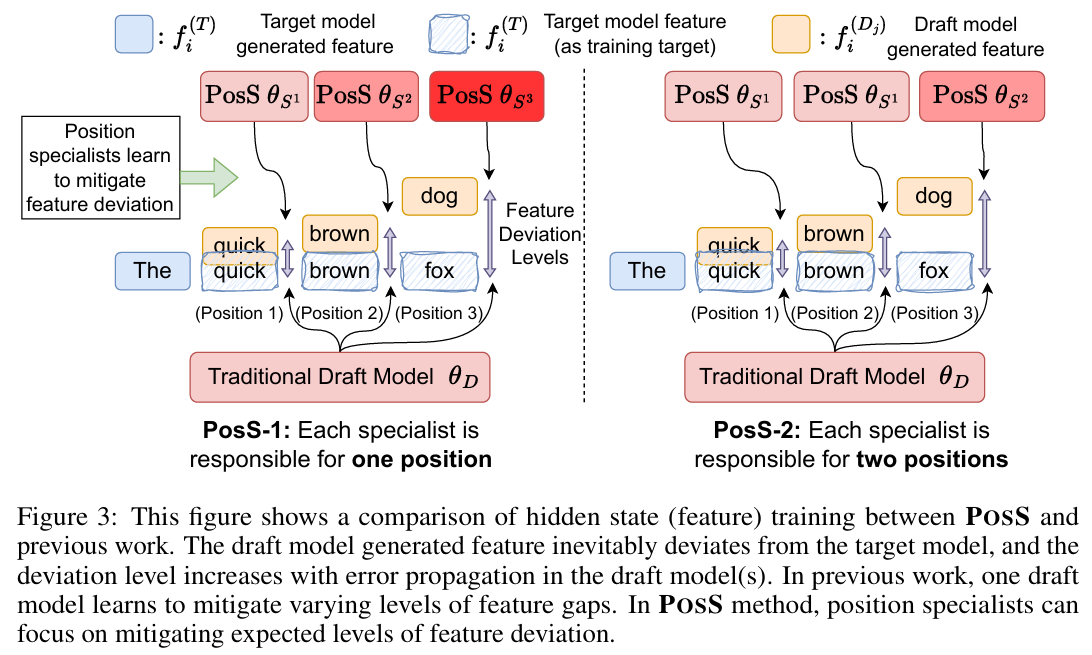
POSS는 초기 위치의 pos-acc를 유지 시키면서, 후반부 위치의 예측 정확도를 향상시키고자 했다. POSS는 여러 개의 위치 특화 draft layer로 구성이 되어 있고, 이를 이 논문에서 position specialist라고 부른다. 각 specialist는 특정 위치나 여러 연속 된 위치의 토큰을 담당하며, 자신에게 할당 된 위치에서 draft 토큰을 생성하도록 학습된다.

각 specialist가 담당하는 위치 개수가 $n$ 이라고 할 때, POSS- $n$ 은 각 specialist가 $n$ 개의 위치를 담당함을 의미한다.

예를 들어, POSS- $i_{i=1}^3$ 이 있다고 한다면, 각 specialist는 각각 $x_{t+1}$ , $x_{t+2}$ , $x_{t+3}$ 위치의 draft 토큰을 예측하도록 할당이 된다.

위 그림은 POSS가 단일 draft 모델보다 왜 더 효과적인지를 설명해준다. trainig이 잘 되어 있더라도, draft 모델이 생성한 hidden state는 target 모델의 feature와 점점 더 차이가 발생하게 된다. 이러한 feature의 편차는 draft가 진행 될수록 누적 된 오차로, 위 그래프에서 보라색 화살표를 의미한다. POSS는 각 위치에서 specialist가 예측 가능한 범주의 feature 편차를 다룰 수 있기 때문에 각 위치에 특화 된 subtask 형태로 분할이 되고, 이를 통해 정확한 draft 예측이 가능해진다.

POSS-n의 Loss Function

POSS의 specialist를 학습 시키기 위해서 필요한 loss function은 크게 3가지로 분류 된다.

Token-level loss
Feature-level loss
Top-K distillation loss

위 3가지 loss에 하이퍼파라미터 두 가지를 추가하여 다음과 같이 전체 loss가 구성이 된다. 이 때, 하이퍼파라미터 $w=0.1$ , $K=10$ 으로 보통 설정을 한다.

L_{total} = L_{feature} + w \times L_{token} + L_{Top-K}

1. Token-level loss

Token-level loss은 정답 토큰을 맞추는 loss를 cross-entropy를 이용하여 만들었다. 그렇기 때문에 이 loss의 역할은 draft 모델이 올바른 단어를 예측하였는가를 의미한다.

L_{token} = CrossEntropy(P(x_{t+i+1}), \hat P(x_{t+i+1}))

여기서 각각의 확률 분포는 다음을 의미한다.

$P(x_{t+i+1})$ : 해당 specialist가 예측한 확률 분포
$\hat P(x_{t+i+1})$ : target 모델이 예측한 확률 분포

그리고 각 확률 분포는 다음과 같이 feature와 specialist index를 이용하여 구할 수 있다.

P(x_{t+i+1}) = Head(f_{t+i}^{S_{\lceil (i+1)/n \rceil}})

\hat P(x_{t+i+1}) = Head(f_{t+i}^{T})

여기서 $f_{t+i}^{T}$ 는 target feature를 의미한다. 그리고 $f_{t+i}^{S_{\lceil (i+1)/n \rceil}}$ 는 해당 위치를 담당하는 specialist의 feature를 의미한다. $\lceil (i+1)/n \rceil$ 은 해당 위치 $i$ 를 담당하는 specialist의 index를 결정한다. 예를 들어 $n=2$ 라면, 아래와 같이 담당하는 index가 결정이 된다.

specialist S1 : 0, 1 index
specialist S2 : 2, 3 index
specialist S3 : 4, 5 index

각 feature는 다음과 같이 계산이 된다.

f_{t+i}^{T} = \theta_T([x_{t+i};\ f_{t+i-1}^{T}],\ [x_{t+i-1};\ f_{t+i-2}^{T}],\ ...\ ,\ [x_{1};\ f_{0}^{T}])

f_{t+i}^{S_{\lceil (i+1)/n \rceil}} = \theta^{S_{\lceil (i+1)/n \rceil}}([x_{t+i};\ f_{t+i-1}^{S_{\lceil (i+1)/n \rceil}}],\ ...\ ,\ [x_{t+1};\ f_{t}^{S_1}],\ [x_t;\ f_{t-1}^T],\ ...\ ,\ [x_1;\ f_0^T])

specialist의 feature 수식이 많이 복잡한데, 각 입력은 토큰 위치 $t$ 를 기점으로, 다음과 같이 구성이 된다.

$t+1$ ~ $t+i-1$ 까지는 누적 오차가 존재하는 이전 specialist가 만든 feature를 의미한다.
$t$ 이하는 target 모델이 가지는 정확한 feature를 의미한다.

2. Feature-level loss

feature-level loss는 feature간 거리를 줄이기 위해 smooth L1을 이용하여 구성이 된다. 그렇기 때문에 draft 모델 내부 hidden state가 target 모델과 얼마나 비슷한지를 나타내는 역할을 갖게 된다.

L_{feature} = SmoothL1(f_{t+i}^{T}\ ,\ f_{t+i}^{S_{\lceil (i+1)/n \rceil}})

이 loss를 통해 specialist는 training 도중에 이미 이전 단계에서 편차가 존재하는 feature를 입력으로 받아서 학습하기 때문에, 추론 시 누적된 오차를 완화 시킬 수 있다.

3. Top-K distillation loss

Top-K distillation loss는 상위 확률 토큰만 비교하는 distillation loss이다. 이는 draft 모델이 중요한 토큰 확률 분포를 target과 얼마나 비슷하게 유지하는지를 나타낸다. HASS에서 제안 된 방식과 동일하게 적용이 되며, target 확률 분포에서 상위 $K$ 개의 토큰만 선택하여 cross-entropy를 계산하는 방식이다.

L_{Top-K} = CrossEntropy_{\ Top-K}(P(x_{t+i+1})\ ,\ \hat P(x_{t+i+1}))

Position Specialist의 계산 비용

POSS를 사용하기 위해서는 다음 2가지 computational overhead가 발생 할 수 있다.

GPU 메모리 사용 증가
specialist switching으로 인한 latency

GPU memory의 경우, position specialist가 증가 할수록 당연히 사용량도 증가하게 된다. 하지만 specialist는 하나의 transformer layer로 만들어져 있기 때문에 target 모델 크기 대비 무시할만한 수준이다. 보통 논문에서 사용 된 8B 모델 기준으로 specialist 하나가 갖는 모델 크기는 218M 수준이였다고 한다.

POSS의 specialist는 EAGLE-2의 단일 draft와 동일한 구조를 사용한다. 그렇기 때문에 draft 단계당 계산 시간은 동일해야 한다. 하지만 실제로는 KV cache가 specialist끼리 공유 되지 않고, 파라미터를 전환 시키는 로딩 오버헤드가 있기 때문에 약간의 오버헤드가 더 존재한다고 한다. 그럼에도 position specialist로 인한 acceptance length 증가의 이득이 더 크기 때문에 무시할 수 있는 수준이라고 한다.

실험 결과

POSS의 실험을 위해서 EAGLE-2와 동일하게 6개의 데이터셋으로 speed-up ratio와 평균 acceptance length를 측정하였다. 모델은 LLaMA-3 8B instruct 모델과 LLaMA-2 13B chat 모델을 사용하였다. 추론 시에는 Sequoia 논문에서 사용 된 tree drafting을 사용하였으며, LLaMA-3에서는 tree depth를 6, 2에서는 7을 사용하였다.

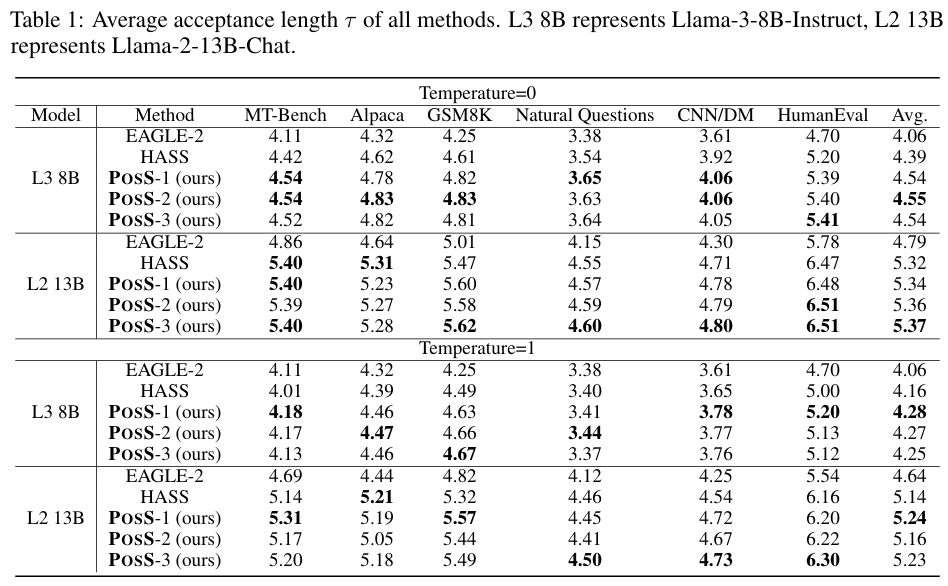
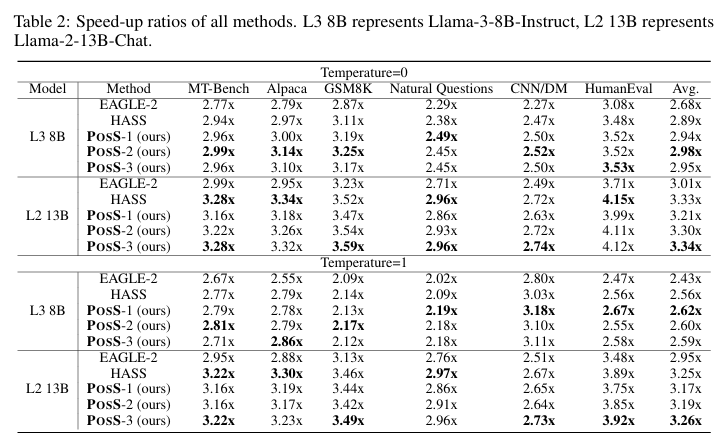
위 두 표는 각각 다양한 모델과 비교군 (EAGLE-2와 HASS)에서의 평균 acceptance length와 speed-up ratio를 나타냈다. temperature 값을 바꾸더라도 POSS가 비교군들에 비해 더 높은 acceptance length와 speed-up을 달성했다. LLaMA-2 13B의 경우, feature representation이 좋게 생성되기 때문에 상대적인 POSS의 장점이 줄어들긴 하더라고 POSS-3의 성능이 제일 좋았다.

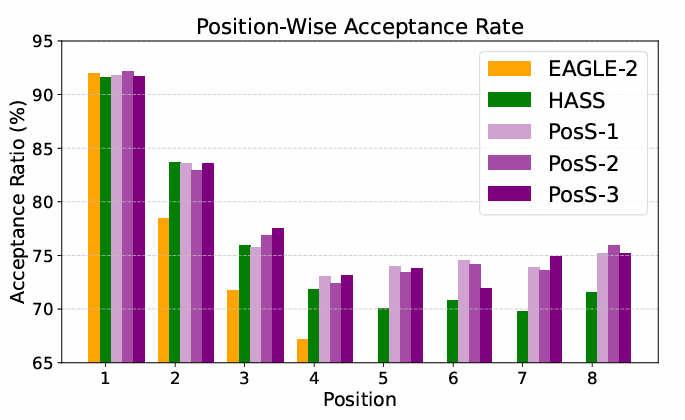
위 그래프는 draft depth가 8인 상태에서, 각 모델의 pos-acc를 비교한 그래프이다. EAGLE-2는 위치를 일반화 시키는 능력이 제일 떨어지기 때문에 5번째 부터 pos-acc가 급격하게 떨어진다. HASS는 첫 4개까지는 적절한 pos-acc가 유지 되지만, 그 이후부터는 단일 draft 모델을 사용하기 때문에 성능이 떨어진다. POSS는 모든 variant가 마지막 위치가지 높은 pos-acc를 유지한다. 이는 POSS가 specialist로 인해 위치별 편차를 줄일 수 있기 때문이다.

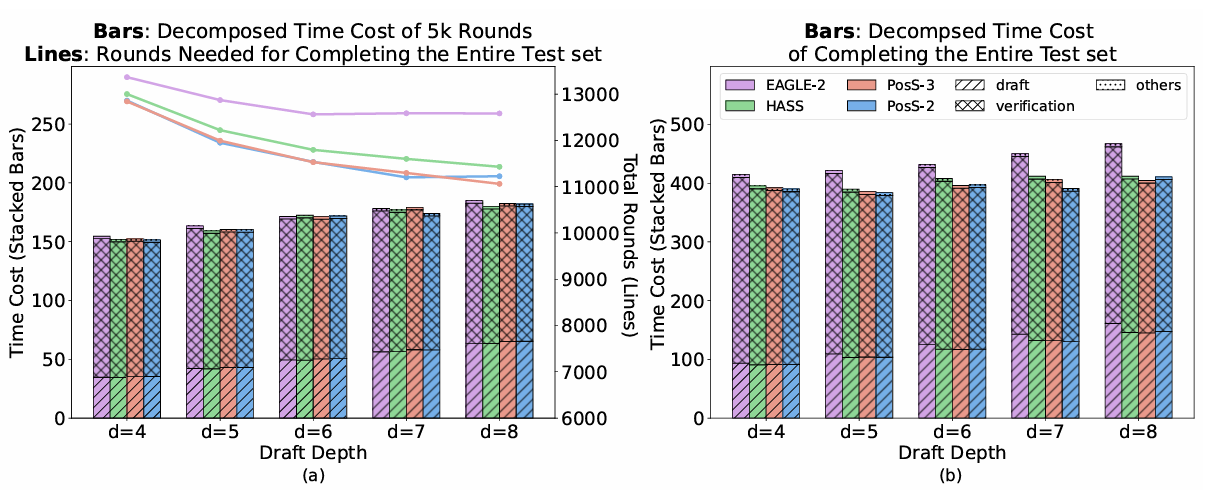
위 그래프는 POSS의 computational overhead에 관련 된 그래프이다. 왼쪽은 5000 라운드 동안 draft depth별 계산 시간을 표시한 결과로, EAGLE-2에 비해 낮고 HASS에 비해 약간의 오버헤드만 보였다. 또한 왼쪽 그래프의 선은 draft 전체 생성에 필요한 총 라운드 수를 의미한다. POSS가 다른 비교군에 비해 라운드 수 또한 적음을 알 수 있다. 오른쪽 그래프는 전체 decoding에 소모 되는 시간을 나타낸 것으로, POSS가 비교군들에 비해 낮은 latency를 갖는데, 이는 라운드 수 감소로 얻는 효율 향상이 POSS의 오버헤드를 충분히 상쇄하고도 남는다는 것을 보여준다.

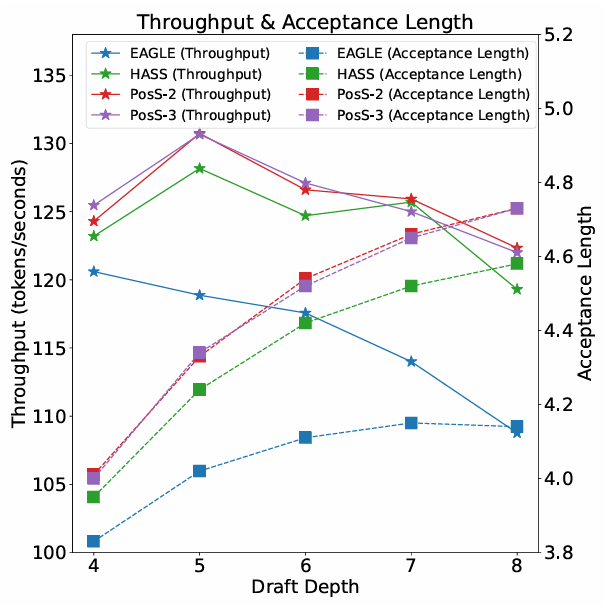
마지막으로 서로 다른 draft depth에서 throughput과 평균 acceptance length를 비교한 그래프이다. draft depth가 커질수록 평균 acceptance length는 증가하지만, 개선 폭은 점점 줄어든다. 그렇기 때문에 throughput의 최적 지점이 존재하는데, POSS의 경우 8번째 위치에서 최적의 speed-up을 달성했다.

결론 및 고찰

이 논문을 읽으면서 POSS를 소개 했던 그분의 아이디어 모티베이션을 어느정도 이해 할 수 있을 것 같다. (물론 나도 이에 대한 다른 의견이 몇가지 있기 때문에 내일 의논을 해볼 생각이지만...) EAGLE-2의 시점에서 성능이 개선이 된 것 같긴 한데 좀 더 다른 모델을 이용한 실험이 있었으면 좋겠다는 생각이 들었다. MoE 관련 논문을 보면서 하도 데이다보니까 이 논문도 과연 다른 모델에서도 잘 될까라는 생각이 들었다.