Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity

Hyunjoon Jeong·2025년 7월 27일

목록 보기

4/13

오늘 리뷰할 논문은 Switch Transformer로 MoE와 관련된 논문이다.
Mixtral과 DeepSeek의 등장으로 인해 MoE 구조에 대한 연구가 ML System 분야에서도 많이 이루어지게 되었는데, 오늘은 우선 그 논문들을 이해하기 전에 MoE에 대한 지식을 쌓을 겸, Switch Transformer를 다뤄볼까 한다.

https://www.jmlr.org/papers/v23/21-0998.html

Sparsely-Activated Expert Model

보통 ML 모델의 파라미터 수가 클수록 더 많은 feature 반영이 가능하기 때문에 성능이 더 좋아진다. 물론 항상 모든 조건에서 모델의 파라미터가 많다고 좋은 것은 아니긴 하지만, 해당 논문에서는 모델의 파라미터가 많으면 성능이 좋다는 것을 전제로 두고 있다.
하지만 모델의 파라미터가 많고 밀집 되어 있다면 아무리 병렬 연산에 특화가 되어 있는 GPU라 할지라도 계산 속도가 느려질 수 밖에 없을 것이다. 그래서 파라미터를 밀집 시키는 방식 대신, sparsity를 부여하여, 모델의 크기는 키우면서 계산 속도를 최적화 하는 방식이 제안 되었다.이러한 상황에서 저자들은 input 값에 대해서 항상 모든 sparse parameter가 활성화가 되는 것이 아니라는 점을 발견했다.
저자들이 제안하는 Sparsely-Activated Expert Model은 여기에서부터 시작한다.

Switch Transformer

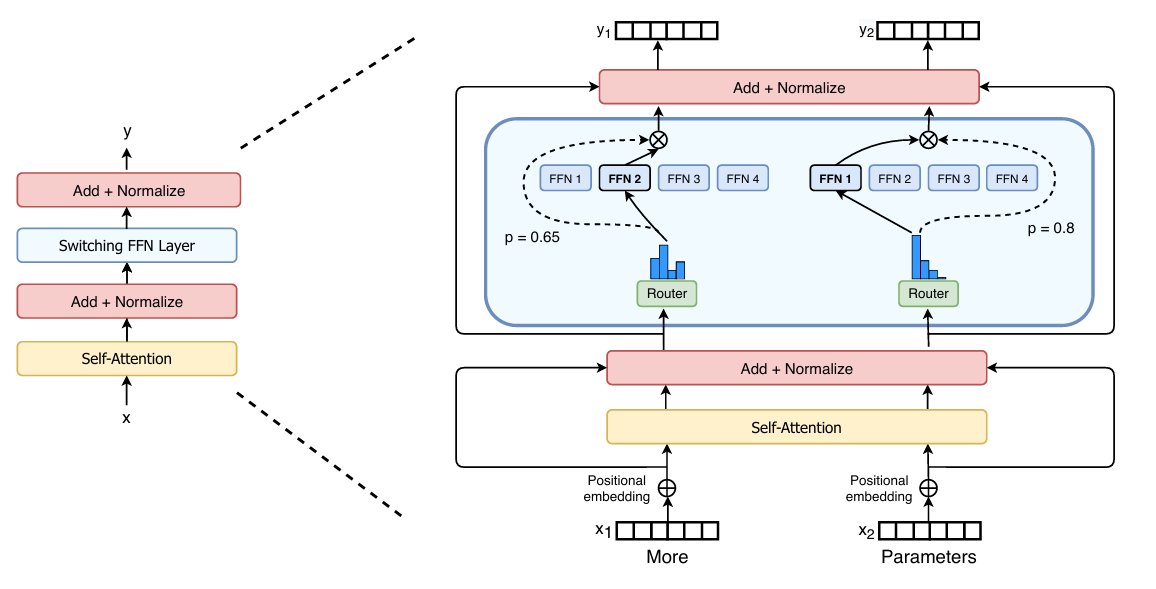
논문에서 제안하는 Switch Transformer의 구조는 매우 간단하다. 위 그림과 같이 기존에 Feed-Forward에 해당하는 Linear 레이어를 Sparse Feed-Forward로 교체하고, 그 앞단에 Switch Router가 포함 된 MoE로 변경한 것이 전부이다. 우선 MoE Routing 방식이 어떻게 다른지부터 살펴보자.

기존 MoE Routing

어떤 입력 토큰 $x$ 가 주어졌다고 가정하자. 그리고 N개의 expert가 주어진다면 $x$ 를 처리할 $N$ 개의 expert 집합을 다음과 같이 수식으로 표현 할 수 있다.

\{E_i(x)\}_{i=1}^N

그래서 토큰 $x$ 에 대해서 저 expert 중 특정 몇개의 expert만 선별해서 계산을 진행해야 한다. 이 때, 확률 계산을 통해 선별해서 토큰이 어느 expert를 통과 할지 결정하는 작업을 MoE Routing이라고 부른다. 만약 Routing을 수행하는 가중치 행렬을 $W_r$ 이라고 정의한다면, 토큰 $x$ 에 대한 logits 값은 아래와 같이 될 것이다.

h(x) = W_rx

각 토큰이 특정 expert ( $i$ 번째 expert)에 routing 되는 확률은 softmax를 통해 정규화가 되어 다음과 같이 계산하게 된다.

p_i(x) = \frac{e^{h(x)_i}}{\sum_{j=1}^{N} e^{h(x)_j}}

이렇게 각 expert로 토큰이 routing 될 확률을 구하게 되는데, 보통 가장 확률이 높은 순서대로 $k$ 개 만큼 선택한다. 이를 top-k Routing이라고 부른다.

그러면 이제 각 expert를 선택 할 확률을 구하고, 어떤 expert들이 활성화가 될 지 정해졌다. 남은 것은 MoE에 대한 토큰의 output을 구해야 한다.

y=\sum_{i\in T}p_i(x)E_i(x)

선택 된 $k$ 개의 expert가 모여 있는 집합을 $T$ 라고 한다면, MoE의 출력 값은 활성화 된 모든 expert들을 수행한 값과, 그 확률의 weighted sum으로 정해지게 된다.

즉, MoE는 선택 된 $k$ 개의 expert만 활성화 시키고,
이들의 출력을 게이트 값으로 가중합(weighted sum) 하여 최종 출력을 생성한다.

Switch Routing

앞서 언급한 top-k routing 방식은 k > 1 이상이 되어야 non-trivial한 gradient가 발생한다는 연구 결과가 있었다. 즉, expert 2개 이상이 서로 비교가 되어야 유의미한 결과가 나온다는 것이다.

하지만 Switch Transformer는 오직 하나의 expert ( $k=1$ )로 routing 시키는 전략을 취했다. 이로 인해 얻을 수 이점은 다음과 같다.

Routing을 위한 연산량이 줄어들고 구현이 간단해진다.
각 expert에서 사용 할 수 있는 batch size가 적어도 2배 이상 커진다.

Expert Capacity

Switch Transforemr는 각 expert마다 처리 할 수 있는 최대 토큰의 수가 정해져있다. 그 이유가 이 논문이 TPU에서 실행 되는 것을 고려 했기 때문이라고 한다. TPU의 경우, 모든 연산을 런타임에서 수행 할 때 사용 되는 Tensor shape는 compile time에 결정 되기 때문이다.
그로 인해 각 expert가 처리할 수 있는 최대 토큰량을 expert capacity라는 이름으로 정의하고, 다음과 같이 계산한다.

expert\ capacity = \frac{tokens per batch×capacity factor}{number\ of\ experts}

capacity factor의 경우, 1.0값이 넘어가게 되면 토큰이 각 expert에게 균등하게 분배 되지 않을 확률이 커지기 때문에, 이를 대비해서 여유 버퍼를 준비하게 된다.

만약 특정 전문가에게 너무 많은 토큰이 할당 되는 경우, expert capacity를 넘어서는 해당 토큰은 dropped token으로 간주되어 expert 연산을 하지 않고, residual connection을 통해 다음 레이어로 전달 된다.

너무 많은 dropped token이 발생하는 경우, capacity factor를 증가 시켜서 위 그림처럼 각 expert가 처리하는 토큰량을 증가 시킬 수 있다. 하지만 이런 경우, expert 하나가 더 많은 연산량을 처리해야 하는 문제가 발생하기 때문에, 이는 trade-off로 간주된다.

Auxiliary Loss

MoE의 문제점 중 하나는, 토큰의 load balancing 문제이다. 특정 expert 방향으로 대부분의 token이 몰리게 되면 학습 효율이나 정확도에 문제가 발생 할 수 있다. 이를 해결하기 위해 Switch Transformer는 각 switch layer가 학습하는 도중에 발생한 loss에 아래와 같은 Auxiliary Loss를 추가하였다.

Auxiliary\ Loss = \alpha\sum_{i=1}^N f_iP_i

Auxiliary Loss를 계산하기 위해서는 두 가지 파라미터 연산이 필요하고, 그 수식은 아래와 같다.
전체 expert의 수가 $N$ , batch size를 $B$ , 토큰 크기를 $T$ 라고 했을 때,

f_i=\frac{1}{T}\sum_{x\in B}1\{\argmax{p(x)}=i\}

P_i=\frac{1}{T}\sum_{x\in B} p_i(x)

$f_i$ 는 실제로 몇 개의 토큰이 expert $i$ 에게 갔는지를 나타낸다. 즉, 토큰이 어느 전문가에게 얼마나 몰렸는지를 나타낸다. $P_i$ 는 모델이 계산한 expert $i$ 의 선호 확률의 평균을 나타낸다. 즉, 모델이 각 expert를 얼마나 좋아했는지를 나타낸다.

Load balancing은 모든 expert에게 똑같이 보내는 것이 제일 이상적이다. 따라서 위에 두 수식은 다음과 같은 값이 되기를 원할 것이다.

f_i=\frac{1}{N}\ \ \ P_i=\frac{1}{N}

결국 실제 토큰 분배( $f$ )가 모델의 의도( $P$ )와 비슷해지고, 둘 다 골고루 분배가 되어야 좋다. 따라서 Auxiliary Loss의 의도는 두 벡터의 유사도를 보고, 불균형한 경우, 페널티를 주는 것이 의도이다.

Auxiliary Loss 연산을 보면 앞에 특정 하이퍼파라미터 $\alpha$ 값이 존재한다. 만약 Auxiliary Loss가 너무 크다면 모델이 load balancing에만 신경을 쓰고 training에 악영향을 줄 수 있다. 그렇다고 너무 작다면 load balancing이 망해버린다. 따라서 $\alpha$ 값은 적절한 값을 사용해야 하고, 이 값은 실험적으로 $10^{-2}$ 값이 적절하다.

Training & Fine-tuning Techniques

Selective Precision

보통 Swtich Transformer처럼 hard-switching (Top-1으로 타이트하게 routing 하는 경우)을 사용 할 때, 작은 값 변화에도 민감한 softmax로 인해 float16을 사용 할 경우 학습이 불안정한 문제가 발생한다. 그로 인해, 이전 연구는 MoE Transformer를 float32로 학습을 시도했다. 하지만 이는 GPU 사이에 통신이 비싸지는 문제가 발생한다.

Switch Transformer는 이런 문제를 해결하기 위해 특정 부분에서만 float32로 캐스팅하여 학습을 했다고 한다. router에 입력 토큰이 들어 갈 때 float32로 변환 하고, router는 이를 이용해 expert 연산 선택과 재결합에 사용 되는 dispatch, combine tensor를 생성한다. 이 때 발생하는 dispatch, combine tensor는 다시 float16으로 변환 되고, 결국 통신에 참여하는 tensor는 float16이 된다.

Smaller Parameter Initialization for Stability

보통 학습 파라미터를 초기에는 평균 0값을 가지고, 표준 편차가 $s/\sqrt{n}$ 인 truncated 정규분포에서 값들을 추출하여 초기화 한다. 이 때, $s$ 는 scale 파라미터이고, $n$ 은 weight tensor의 입력 유닛 수를 의미한다.
보통 일반적인 Transformer는 $s=10$ 을 사용한다. 하지만 이는 학습이 불안정해지고, 매 실험마다 성능이 달라질 수 있기 때문에, Switch Transformer는 이 값을 1로 사용했다고 한다.

Regularizing large sparse models

보통 NLP 모델은 pre-training 이후에 목적에 맞게 fine-tuning을 수행한다. 하지만 pre-training에 수행 되는 데이터에 비해 downstream 작업의 데이터가 상대적으로 작다보니 overfitting이 발생할 수 있다는 문제점이 있다. 이를 방지하기 위해서, 보통 transformer에서는 각 레이어를 dropout 하는 방식을 사용한다.

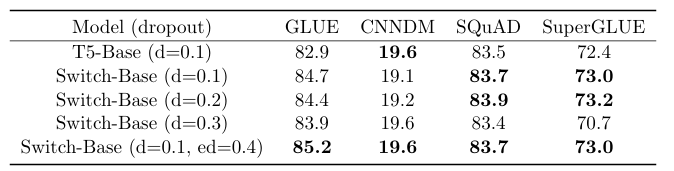
하지만 Switch Transformer는 FLOPS가 동일한 dense baseline에 비해 더 많은 파라미터를 갖고 있기 때문에 overfitting 문제가 더 심할 수 있다. 따라서 이를 해결하기 위한 방법은 expert layer의 중간 feed-forward의 dropout의 비율을 다른 레이어보다 높게 설정 하는 것이다.

위 표는 모든 레이어에 dropout을 동일하게 적용 했을때와 expert에서만 높게 설정한 결과를 보여준다. 단순하게 모든 레이어의 dropout을 키우는 경우, overfitting이 줄어 들더라도 모델 전체의 표현력도 약화된다. 특히 attention이나 non-expert까지 약화시키면 전체 성능 또한 감소한다.

그래서 파라미터 수가 많은 expert의 feed-forward에서 overfitting이 대부분 발생하기 때문에 이에 대해서 과감하게 dropout을 적용하고, attention 같은 다른 레이어의 비율을 적게 유지해서 표현력은 그대로 유지 할 수 있도록 조정할 수 있다.

또한 dropout은 학습 도중에 일부 네트워크를 랜덤하게 꺼서 여러 모델을 학습하는 앙상블 효과를 준다. 이를 expert에 비추었을 때, expert dropout은 여러 expert 조합을 학습하게 해서 특정 expert만 사용하는 경향을 방지 할 수 있게 된다.

실험 결과

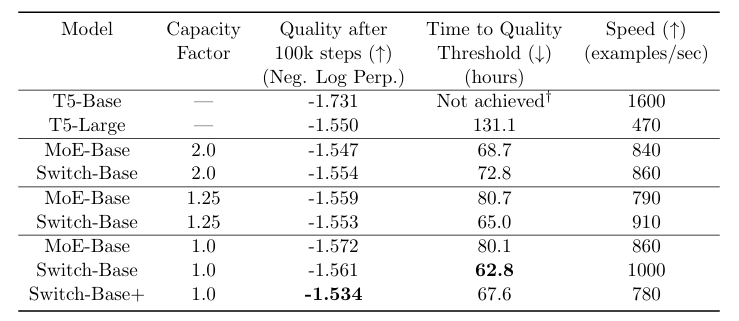
해당 논문에서 실험은 T5 모델을 이용하였고, 이를 각각 기존 MoE의 top-2 방식과 switch transformer를 이용해 training한 결과를 이용하였다.

우선 학습 속도의 경우, Switch Transformer > MoE > Dense 순서대로 연산 효율이 좋았다. 특히 capacity factor를 적절하게 조정 한 경우, 처리량이 16%까지 증가하는 것을 볼 수 있었다.

결론 및 고찰

기존에 내가 대략적으로 알고 있던 MoE의 경우, top-k가 2 이상인 경우만 가정했었는데, 이 논문의 경우 top-1으로 hard-routing을 하는 논문이라 재밌었다. 다만 아무래도 ML System이 아니라 DNN 자체에 관한 내용이다보니, 아무래도 나에게는 방법론에서 흥미가 떨어지는 것 같았다. 그래도 MoE를 어느정도 이해 하게 되었으니 그걸로 만족해야하나 싶다.