Linear Algebra - 4주차 1/2

사실 3주차 포스팅 이후로 복습을 하지 않고 일주일 동안 버닝을 했더니 그 사이에 완강을 해버렸다. 복습 좀 제때 하자

DISCLAIMER: 아래 내용은 오로지 Coursera 강의를 토대로 제가 이해한 대로 정리한 것이기 때문에 부정확하거나 설명이 그닥 친절하지 않은 부분이 있을 수도 있습니다.

---

아인슈타인 표기법(Einstein summation convention)

아인슈타인 표기법(Einstein summation convention)은 행렬 공식을 간결하게 표현하는 또 다른 방법이라고 볼 수 있다. 대충 시그마를 생략하는 거라고 생각하면 될 것 같다.

다음과 같은 행렬 $A$와 $B$가 있다고 하자.

$A=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}$, $B=\begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{nn} \end{bmatrix}$

이 두 행렬의 곱 $AB$ 중에서 2열 3행에 위치한 $(ab)_{23}$의 값은 다음과 같이 구할 수 있다.

$(ab)_{23} = a_{21}b_{13} + a_{22}b_{23} + \dots + a_{2n}b_{n3}$

아인슈타인 표기법을 이용하면 이 과정을 모든 원소에 대해서 다음과 같이 정리할 수 있다.

$(ab)_{ik} = \sum_{j=1}a_{ij}b_{jk} = a_{ij}b_{jk}$


아인슈타인 표기법으로 내적(dot product) 공식을 간단히 할 수 있다.

$u = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix}$, $v = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}$가 있을 때, 이 두 벡터의 내적은 다음과 같이 표현할 수 있다.

$u \cdot v = \sum_{i=1}u_iv_i = u_iv_i$

---

행렬곱과 역행렬을 이용한 기저변환

사영벡터를 이용하는 방법 뿐만 아니라, 행렬곱과 역행렬을 이용하여 기저변환을 하는 방법도 있다.

기저벡터가 $\hat e_1=\begin{bmatrix} 1 \\ 0 \end{bmatrix}$, $\hat e_2=\begin{bmatrix} 0 \\ 1 \end{bmatrix}$인 벡터공간이 있다고 하자. 또 다른 벡터공간(강의에서는 판다의 벡터공간이라고 부른다)의 기저벡터는 기존 벡터공간에서 표현했을 때 $\begin{bmatrix} 3 \\ 1 \end{bmatrix}$, $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$라고 하고, 행렬 $\begin{bmatrix} 3 & 1 \\ 1 & 1 \end{bmatrix}$로 나타낼 수 있다.

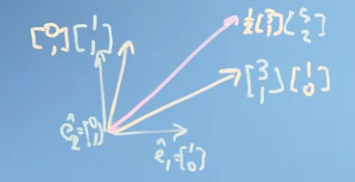
판다의 벡터공간 안에서 정의된 벡터 $\begin{bmatrix} \frac{3}{2} \\ \frac{1}{2} \end{bmatrix}$가 있다. 이 벡터를 $\hat e_1$, $\hat e_2$로 정의된 기존 벡터공간의 값으로 변환하려면 다음과 같이 하면 된다.

$\begin{bmatrix} 3 & 1 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} \frac{3}{2} \\ \frac{1}{2} \end{bmatrix} = \begin{bmatrix} 5 \\ 2 \end{bmatrix}$

비슷한 방식으로 변환된 값을 다시 판다의 공간으로 변환을 하려면 $\begin{bmatrix} 3 & 1 \\ 1 & 1 \end{bmatrix}$의 역행렬을 곱해주면 된다.
$\frac{1}{2}\begin{bmatrix} 1 & -1 \\ -1 & 3 \end{bmatrix}\begin{bmatrix} 5 \\ 2 \end{bmatrix} = \begin{bmatrix} \frac{3}{2} \\ \frac{1}{2} \end{bmatrix}$

---

직교행렬(orthogonal matrix)과 전치(transpose)

전치(transpose)라는 것은 행렬을 대각선 기준으로 뒤집는 것을 의미하고, T를 사용하여 표현한다.

$A_{ij}^T = A_{ji}$

$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}^T = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}$

벡터 $a_1$, $a_2$, $\cdots$, $a_n$으로 이루어진 $n \times n$ 행렬 $A$가 있다고 하자. $A$를 구성하는 벡터들은 다음과 같은 성질을 갖는다.

$a_i \cdot a_j = 0 \space (i \neq j)$
$a_i \cdot a_j = 1 \space (i = j)$

즉, $A$의 벡터들은 모두 orthogonal하며 unit length를 가지므로 orthonormal basis set를 이룬다. 이러한 행렬을 직교행렬(orthogonal matrix)라고 부른다. 참고로 $det A = \pm 1$이다.

직교행렬의 행과 열은 모두 orthonormal하다. 또한 orthonormal basis set을 전치(transpose)한 결과 값도 orthonormal하다.

직교행렬 $A$의 전치행렬은 $A$의 역행렬과 동일하다. ($A^T=A^{-1}$ ↔ $A^TA=I$)

---

필기 첨부