로봇의 움직임을 알아보기 전에 우리는 '로봇이 어디에 있는가?'라는 질문에 답을 해야한다. 이에 대한 답은 로봇의 configuration에서 시작된다.

Configuration

책에서는 Configuration을 다음과 같이 설명한다.

robot's configuration: a specification of the positions of all points of the robot.

해석하면 로봇의 Configuration은 로봇의 모든 점의 위치를 정확하게 명시하는 것이다.
로봇의 움직임을 분석하기 위해 보통 로봇을 강체인 링크와 그 링크를 연결해주는 관절(joints)로 구성한다.
여기서 우리는 강체에 모양을 알고 그 모양이 변하지 않기 때문에 로봇의 configuration을 표현하기 위해 많은 숫자가 필요하지 않을 수도 있다.

예를 들어 다음과 벽에 고정되어 있고 $\theta$ 만큼 열려있는 문이 있다고 하자

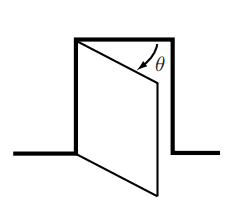
이 문의 configuration은 $\theta$라는 하나의 매개변수로 표현할 수 있다.

이번에는 평면에 앞면으로 놓인 동전을 살펴보자

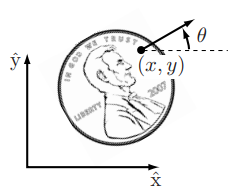
이 동전의 Configuration을 표현하기 위해서는 이 동전의 위치를 표현하는 $x, y$와 동전의 방향을 표현하는 $\theta$가 필요하다.

Degree of Freedom (자유도)

줄여서 dof 한국어로는 "자유도" 라고 한다. 자유도는 로봇의 configuration을 표현하기 위해 필요한 최소한의 실수 매개변수(좌표)의 수이다.

위에 예시에서 문의 컨피규레이션을 $\theta$하나로 표현할 수 있기 때문에 문의 자유도는 1 이다.
평면 위에 놓여진 동전은 $x, y, \theta$임으로 자유도가 3임을 알수있다.

2.1 Degree of Freedom of a rigid Body (강체의 자유도)

시스템의 자유도를 결정하기 위해 다음과 같은 일반적인 규칙을 적용 할 수 있다.

자유도 = (모든 점의 자유도의 합) - (독립적인 제약조건의 개수)

(2.1)

이를 적용하기 위해 위에 동전 예시에서 이번에는 동전 위에 3개의 점을 정해보자

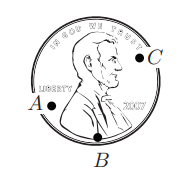
이 평면이 $x-y$좌표계에 있다고 할때 이 3개의 점은 $(x_A,y_A), (x_B,y_B), (x_C,y_C)$로 표현 할 수 있다. 만약 이 3개의 점이 이 평면에서 어디에든 서로 독립적으로 움직일 수 있다면 이 한 점의 자유도는 2임으로 동전의 자유도가 6이 된다. 하지만 동전은 강체임으로 각각의 점 사이에 거리는 모두 일정하다. 그럼으로 다음과 같은 제약조건 식을 세울 수 있다.

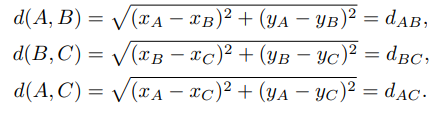
여기에 앞에서 설명한 규칙을 적용하면

동전의 자유도=6(모든 점의 자유도의 합) - 3(독립적인 제약조건의 개수) = 3

이렇게 앞에서 설명한 동전의 자유도와 같은 것을 알 수 있다. 이와같은 방식을 적용하면 3차원에 놓여진 강체의 자유도는 6이라는 것을 알 수 있다.

로봇은 강체로 이루어 졌기 때문에 로봇에서는 위에 규칙을 다음과 같이 나타낼 수 있다.

자유도 = (몸체의 자유도의 합) - (독립적인 제약조건의 개수)

2.2 Degrees of Freedom of a Robot (로봇의 자유도)

로봇의 경우에는 joint가 강체의 자유도를 제한함으로서 로봇의 전체 자유도를 줄인다. 이 관점으로 링크(강체)와 관절의 수를 셈으로서 로봇의 자유도를 결정할 수 있다.

2.2.1 Robot Joints (로봇 관절)

다음은 전형적인 로봇 관절이다.

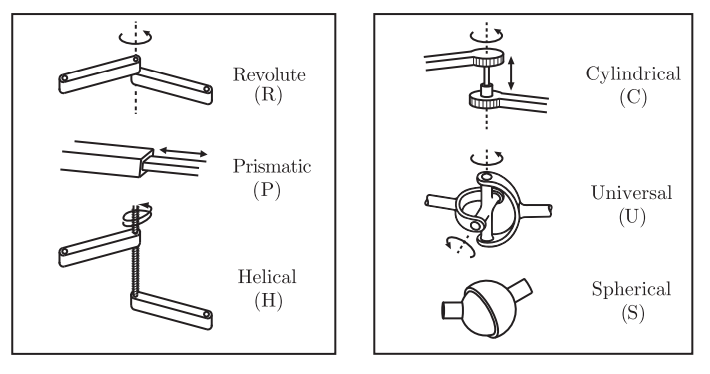
모든 관절은 정확히 두 개의 링크를 연결하며, 세 개 이상의 링크를 동시에 연결하는 것은 허용하지 않는다.

다음은 로봇 관절이 제공하는 자유도 $f$와 제약조건 $c$이다.

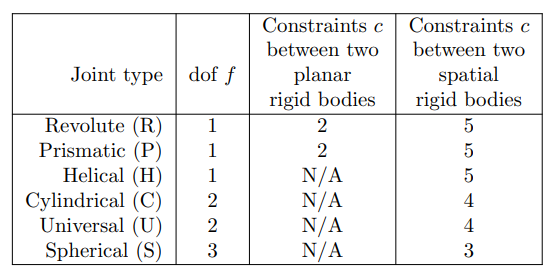
예를 들어 원통형(Cylindrical)관절은 하나의 공간 강체에 다른 강체에 대한 5개의 제약조건을 가함으로서 두 강체 사이에 하나의 자유도를 부여한다. 여기서 2.1에서 설명한 자유도 규칙이 적용되는 것을 알 수 있다.(6-5=1)

2.2.2 Grübler's Formula (그뤼블러의 공식)

링크와 관절로 이루어진 매커니즘의 자유도는 그뤼블러의 공식으로 구할 수 있다.

지면을 링크로 간주할 때 다음의 매커니즘을 봐보자

• 링크의 개수: $N$
• 관절의 개수: $J$
• 강체의 자유도: $m$(공간:=6, 평면:=3)
• 관절 $i$가 제공하는 자유도: $f_i$
• 관절 $i$가 제공하는 제약조건의 수: $c_i$

위에 상황을 2.1.에서 설명한 규칙에 적용하면 로봇의 자유도를 쉽게 구할 수 있는 공식이 나온다.

이 식은 관절 제약조건이 독립이 아니면 성립하지 않으며 이 공식을 그뤼블러의 공식이라고 한다.

아래 그림에 나오는 매커니즘에 그뤼블러 공식을 적용해 보자

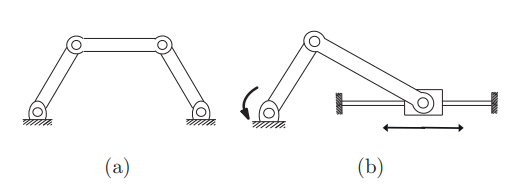
평맨 매카니즘임으로 $m=4$이다.

• (a)의 경우
  $N=4, J=4, f_i = 1$임으로 자유도는 $-3(4-1-4)+4=1$이다.

• (b)의 경우
  2개의 방법으로 분석 할 수 있다.
  1). 3개의 회전형 관절과 1개의 선형관절 그리고 4개의 링크
  2). 2개의 회전형 관절과 1개의 RP관절(회전형 관절과 선형 관절을 연결한 것 $f_i=2$)

더 많은 예제는 본 책에서 볼 수 있다.

open-chain and closed-chain mechanisms

보통 로봇을 개연쇄 메커니즘(open-chain mechanisms)과 폐연쇄 메커니즘(closed-chain mechanisms)으로 구별할 수 있다.
폐연쇄 메커니즘은 위에 (a)와 같이 닫힌 고리를 포함하는 메커니즘이고
개연쇄 메커니즘은 일반적인 로봇팔과 같이 닫힌고리가 없는 메커니즘이다.

2.3 Configuration Space: Topology and Representation

Topology:위상

2.3.1 Configurarion Space Topology

Configuration Space(C-space)

로봇의 모든 가능한 컨피규레이션을 포함하는 n차원 공간을 Configuration space(C-space)라고 한다.

configuration space의 형태에 대해 알아보자.

topologically equivalent (위상 동형)

구의 표면에서 움직이는 점을 생각했을 때 점의 configulation을 위도와 경도로 표현할 수 있으며 이때의 C-Space(configuration space)는 2차원이다.
이번에는 $x-y$ 평면위에 놓인 점을 생각해보자 이번에는 $(x,y)$로 표현하게 되며 C-Space는 2차원이다.

위에서 불 수 있듯이 2개의 C-Space 모두 2차원이다. 하지만 이들은 같은 모양을 갖지 않는다는 것에 주목해야한다. 평면은 무한히 확장되지만 구는 끝을 감싸는 모양이 된다.
이런 경우는 위상 동형이 아니다.

위상 동형이려면 하나의 공간을 자르거나 붙이지 않고 다른 공간으로 연속적으로 변형될 수 있어야한다.
구를 자르거나 붙이지 않고 단순하게 늘려 미식 축구공처럼 타원형으로 만들 수 있기 때문에 이 경우에는 두 공간을 위상 동형이라고 한다.

1차원 공간을 위상적으로 구분해 보면

• 직선(line): $\mathbb {E}$ or $\mathbb {E}^1$, $\mathbb {R}$ or $\mathbb {R}^1$ 으로 표현
  (종점을 포함하지 않는다. (open interval of the line): $(a,b) \subset \mathbb {R}^1$와 위상 동형)
• 원(circle): $S$ or $S^1$ ; $S^n$은 $(n-1)$차원에 있는 구의 $n$차원표면이다.
• 직선의 닫힌 구간(closed interval of the line): $[a,b] \subset \mathbb {R}^1$

공간의 위상은 공간 그 자체의 근본적인 특성이며 공간에서 점을 표현하기 위해 선택하는 좌표와 독립적임을 알아야 한다.

일부 상태 공간은 아래와 같이 낮은 차원들의 집교 곱(Cartesian product)으로 나타낼 수 있다

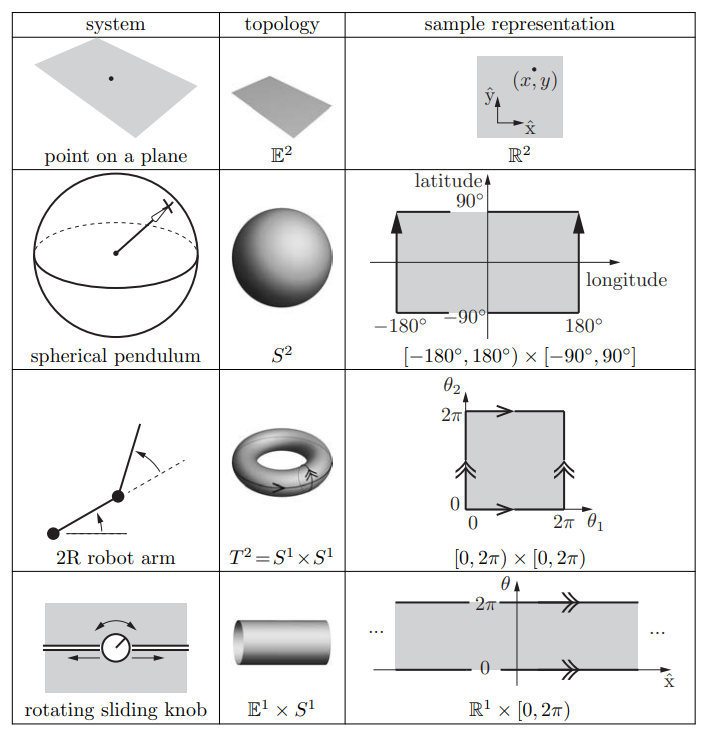
예를들어 평면상의 강체의 configulation은 위치를 나타내는 $(x,y):\mathbb{R}^2$와 방향을 나타내는 $\theta:\mathbb{S}^1$으로 표현됨으로
C-Space는 $\mathbb{R}^2\times\mathbb{S}^1$으로 나타낼 수 있다.

2.3.2 Configuration Space Representation (상태 공간 표현)

explicit parametrization (직접적 매개변수화)

직접적 매개변수화는 $n$차원 공간을 표현할때 $n$개의 매개변수를 사용하는 것이다.
이 경우 매개변수의 특정한 범위에서만 유효하다.
예를들어 위도:$[-90\degree,90\degree]$ 경도:$[-180\degree,180\degree)$로 표현된 구를 생각해 보자

이 경우 북극점, 남극점에서 조금만 움직여도 좌표상에서 큰 변화가 생긴다. 이때의 북극점과 남극점을 이 표현식의 특이점(singularities)라고 한다.
특이점은 좌표의 시간 변화율로 속도를 나타낼 때 특히 문제가 된다. (무한대로 발산 할 수 있다.) 만약 컨피규레이션 표현이 특이점에 절대 도달할 수 없다면 문제가 되지는 않지만 도달할 가능성이 있다면 이 문제를 해결해야 한다.

implicit representation (간접적 표현식)

직접적 매개변수화의 문제를 해결할 수 있는 방법이다.
간접적 표현식은 $n$차원 공간을 표현할때 $n$개 보다 더 많은 변수를 사용하고 이에 제약조건을 걸어 자유도를 제한한다. $n$차원보다 높은 차원의 공간에서 $n$차원을 표현한다고 생각할 수 있다.
예를들어 다음에 다룰 회전행렬(rotation matrixes)가 있다.
회전행렬은 9개의 매개변수와 6개의 제약조건을 사용하여 공간상의 방향을 표현한다.
이 경우 롤-피치-요 각도와 달리 특이점이 없다.

이 외에도 직접적 매개변수화의 문제점을 해결하는 방법이 있다. 이에 대해서는 본책에서 찾아보자

2.3 Configuration and Velocity Constraints (컨피규레이션과 속도 제약조건)

holonomic constraints (홀로노믹 제약조건)

하나 이상의 닫힌 고리를 가진 로봇에서는 보통 직접적 보다 간접적 표현식을 더 쉽게 얻을 수 있다. 다음 예제를 살펴보자

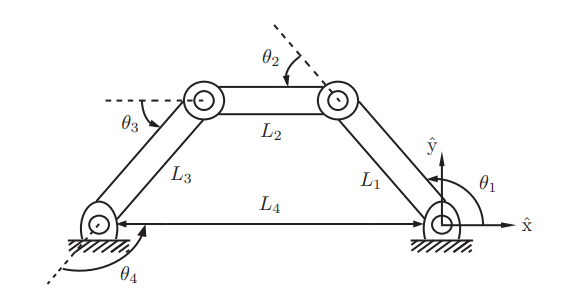
위 예제는 아래와 같이 4개의 변수와 3개의 식으로(제약조건)으로 표현할 수 있다.

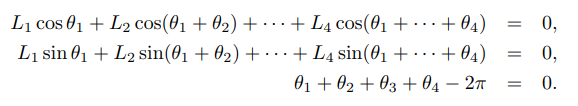
이러한 방정식을 종종 고리 닫힘 방정식(loop-closure equations)라고 한다.
이 해의 모든 집합은 3차원 공간에서 1차원 곡선을 이루며 상태 공간을 구성한다.
이 고리 닫힘 방정식에서 주어지는 $k$개의 독립방정식을 이용하여 고리 닫힘 방정식을 $g(\theta)=0$을 표현해보자 ($k<=n$)

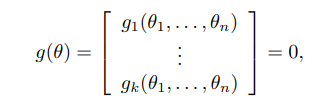
이러한 제약조건을 홀로노믹 제약조건(holonomic constraints)이라고 하며 상태공간의 차원을 줄인다. 이 제약조건이 모두 독립일 때 상태공간은 $n$차원에서 표현된 $n-k$차원 표면으로 볼 수 있다.

Pafaffian constraints (파피안 제약조건)

위에 로봇이 시간 궤적 $\theta(t)$를 따라 움직인다 가정하고 $g(\theta(t))=0$의 양변을 미분해보자

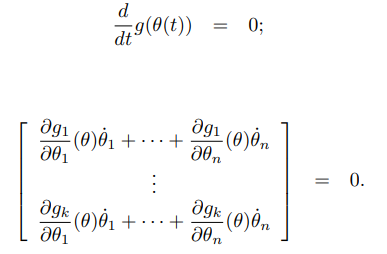
행렬에 열벡터를 곱하는 방식으로 표현하면

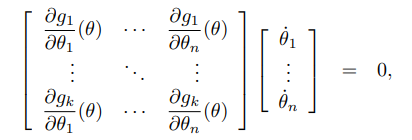
이를 다음과 같이 쓸 수 있다.

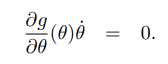
그리고 이를 다음과 같이 써보자

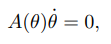
이러한 속도제약조건을 파피안 제약조건(Pafaffian constraints)이라고 한다.

파피안 제약조건에서 $A(\theta)=\frac{\partial g}{\partial \theta} (\theta)$를 만족하는 미분가능한 함수 $g(\theta)$가 존재하는 홀로노믹 제약조건을 적분 가능한 제약조건이라고 부른다.

nonholonomic constraints (비홀로노믹 제약조건)

이번에는 다음과 같이 미끄러짐 없이 평면 위를 구르는 동전을 생각해보자

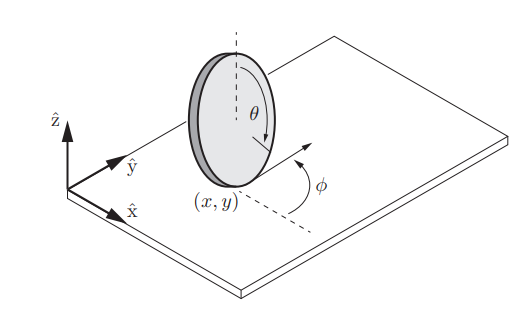
이 동전의 configuration은 $(x,y,\theta,\phi)$로 표현된다.
이 동전의 속력은 $r\dot{\theta}$임으로 속력은 $(r\dot{\theta} cos\phi,r\dot{\theta}sin\phi )$이다. 이 것을 다음과 같은 식으로 정리할 수 있다.

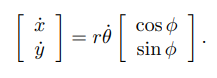
상태공간 좌표를 하나에 벡터 $q=(q_1,q_2,q_3,q_4)^T=(x,y,\phi,\theta)^T$로 표현한다면 다음과 같이 정리할 수 있다.

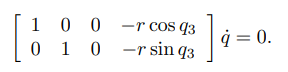
이것은 $A(q)\dot{q}=0$의 형태를 갖는 파피안 제약조건이다.
여기서 $A(q)=\frac{\partial g}{\partial q} q)$를 만족하는 미분가능한 함수 $g(q)$가 존재할려면 함수 $g$는 다음을 만족해야 한다.

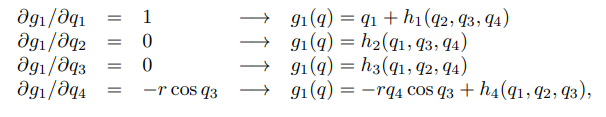
여기서 이런 함수$g$는 존재하지 않는다는 것을 알 수 있다.
즉 이 제약조건은 적분이 불가능하다.
이렇게 적분이 불가능한 파피안 제약조건을 비홀로노믹 제약조건(nonholonomic constraints)이라고 한다.

이 제약조건의 시스템의 속도에는 제한을 주지만 상태 공간의 도달 가능한 차원을 줄이지는 못한다. 이런 비홀로노믹 제약조건은 운동량 보존과 미끄러짐없는 구름에서 볼 수 있다.
이 제약조건은 13장에서 더 자세히 다룬다.

2.5 Task Space and Workspace

Task Space

The task space is a space in which the robot’s task can be naturally expressed.

Task Space는 로봇의 작업이 자연스럽게 표현되는 공간이다. 말 그대로 task가 진행되는 공간이라고 할 수 있을거 같다. 여기서 중요한 것은 Task Space는 로봇과 별개라는 것이다.
예를 들어 로봇의 작업이 평면에 그림을 그리는 것이라면 엔드 이펙터가 어디까지 다을 수 있는 지와는 상관 없이 Task Space는 평면의 실수 2차원 전체가 된다.

여기서 엔드 이펙터란 환경과 상호 작용하도록 설계된 로봇 팔 끝에 있는 장치이며 로봇공학에서 중요한 용어이다.

Workspace

The workspace is a specification of the configurations that the end-effector
of the robot can reach.

Workspace는 로봇의 엔드 이펙터가 닿을 수 있는 configuration이다.
이는 task space와는 반대로 로봇의 형태에 의존적이며 로봇의 Task와는 별개다.

오늘의 영단어

• specify: (구체적으로)명시하다.
• specification: (자세한)설명서, 사양
• real-valued: 실수의
• equality: 등식; 평균, 균등
• coordinate frame: 좌표계
• apparent: 분명한
• noncollinear: 동일선상이 아닌
• sptial: 공간
• via: ~를 통하여
• vary: 다르다
• proposition: 명제; 제의
• distinct: 분명한, 뚜렷한
• concept: 개념
• relate to: ~와 관계가 있다.
• feasible: 실현 가능한
• default representation: 기본 표현식
• primarily: 주로
• numerical: 수치적인
• latitude: 위도
• longitude: 경도
• subset: 부분집합
• deform: 변형시키다
• integrable: 적분시키다