우리는 로봇의 움직임을 분석할 때 로봇의 링크를 강체로 취급하고 그 강체의 위치와 이동을 수학적으로 표현한다.
이번에는 강체의 위치와 이동을 어떻게 표현하는 지에 대해 다룰거다.
이 파트에서 배운 표현이 앞으로 계속 사용되기 때문에 잘 숙지하는 것이 좋다.

이 파트에서는 나의 개인적인 분석과 해석이 들어가기 때문에 본책의 내용과 순서와 설명이 다를 수 있다.

3.1 Rigid-Body Motions in the Plane

평면에서 강체의 표현

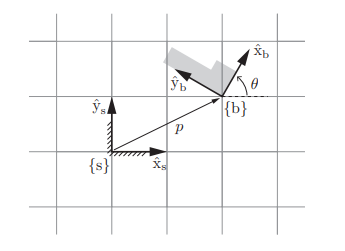
보통 로봇의 강체에 달린 좌표계를 물체 좌표계${b}$로 표현하고
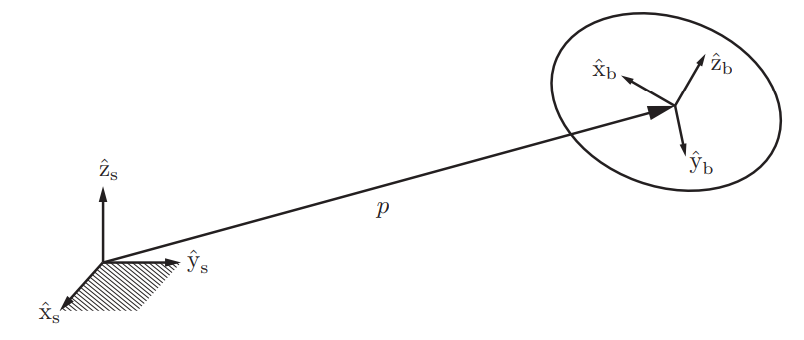
로봇이 놓인 움직이지 않는 공간에 좌표계를 고정 좌표계${s}라고 표현한다.
이런 몰체 좌표계의 움직임을 고정 좌표계에 대해 설명하며 우리는 로봇의 움직임을 설명 할 수 있는 것이다.
물체 좌표계를 고정 좌표계에 대해 표현해 보자

물체 좌표계의 원점을 표현하는 벡터 $p$를 공간 좌표계의 단위축$\hat{x}_s,\hat{y}_s$을 사용하여 다음과 같이 나타낼 수 있다.

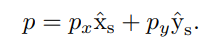
물체 좌표계의 방향을 표현하기 위하여 물체 좌표계의 단위축 $\hat{x}_b,\hat{y}_b$을 고정 좌표계에 대해 다음과 같이 표현해보자.

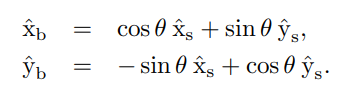
위의 표현들을 벡터와 행렬로 나타내 보자


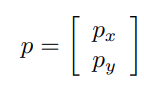
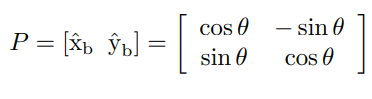
$p$는 물체 좌표계의 위치를 $P$는 물체 좌표계의 방향을 나타낸다.
이렇게 물체좌표계 즉 강체의 위치와 방향을 표현할 수 있다.

똑같은 방법으로 3차원에 있는 강체를 다음과 같이 표현할 수 있다.

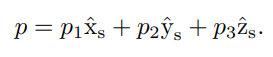
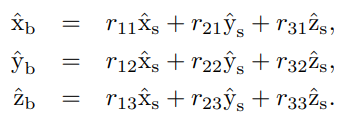
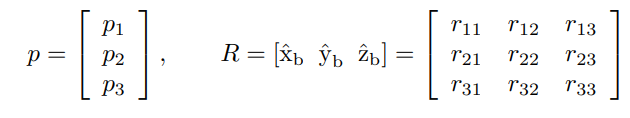
이 정보들은 강체의 자세를 표현하거나 기준 좌표계의 변경, 그리고 벡터나 좌표계를 이동시킬 때 사용될 수 있다. 이에 대해서는 나중에 자세히 다루어진다.

위에서 방향을 나타내는 행렬 $P$와 $R$은 회전행렬(rotation matrixes)이라 불린다. 위에서 볼 수 있듯이 회전행렬의 열벡터가 단위벡터라는 것을 기억하자.

3.2 Rotations and Angular Velocities

회전과 각속도

3.2.1 Rotation Matrixes

회전행렬

2.3.2의 간접적 표현식에서 설명했 듯이 회전행렬은 간접적 표현식을 사용한다. 3차원 공간에서 강체의 방향은 3자유도를 사용하기 때문에 3차원 회전행렬에서 3개의 원소만 독립적으로 정해질 수 있다.

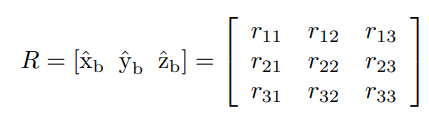
위와같이 3차원 회전행렬은 3 by 3행렬이고 이 행렬의 9개의 원소에 6개의 제약조건이 걸린다. 이 제약조건을 알아보자.

위에서 볼 수 있듯이 회정행렬은 단위축(즉 단위벡터이다.)을 행렬의 열로 사용하기 때문에 각 열들은 서로 orthogonal이다. 즉 크기가 1이고 서로 수직이다.

그럼으로 다음을 만족한다.


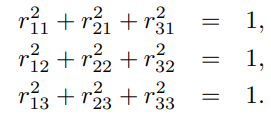
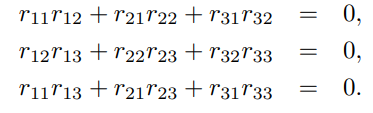
이것이 위에서 말한 6개의 제약조건이 된다.
이렇게 각 열이 orthonormal한 행렬을 orthogonal matrix 혹은 orthnormal matrix라고 한다.

3.2.1.1 Properties of Rotation Matrices

회전행렬의 성질

즉 회전행렬은 orthogonal matrix이다. 이러한 3 by 3 행렬들을 특수직교군(Special Orthogonal Group) $SO(3)$라고 한다. ($SO(2)$은 $2$ by $2$ 회전행렬이다.)

특수직교군은 '군'(group)임으로 다음과 같은 수학적인 군의 성질을 만족시킨다.

추가로 특수직교군은 다음과 같은 성질을 가진다.
특수직교군에 속한 행렬 $R$에 대해

• $R^{-1}=R^T$이고 이 둘 모두 회전행렬이다.
• $det(R)=1$이다.
• 두 회전행렬의 곱 또한 회전행렬이다.
• 벡터$x$에 대해 $y=Rx$는 $x$의 크기와 같다.

3.2.1.2 Uses of Rotation Matrices

회전행렬의 활용

좌표계 {$a$},{$b$},{$c$}가 있을 때 $R_{ab}$는 {$a$}를 기준으로 표현한 {$b$}의 방향이다. 그럼으로 $R_{bc}$는 {$b$}에서 보는 {$c$}의 방향이라고 할 수 있다.

여기서 $R_{ac}R_{ca}=I$ 임으로 $R_{ac}=R_{ca}^{-1}$이다.

이런 회전행렬의 용도는 3가지이다.

(1) (좌표계의) 방향을 표현하기 위해

3.1에서 보았듯이 $R$자체로 방향을 표현할 수 있다.
$R_{bc}$는 {$b$}에서 보는 {$c$}의 방향이며
$R_{bc}$의 열은 {$b$}에서 표현한 {$c$}의 단위축이다. 회전행렬을 설명하는 글을 많이 봐왔지만 이렇게 단위축으로 설명하는 경우는 거의 없었다. 하지만 나는 단위축 해석을 통해 회전행렬을 직관적으로 이해 할수 있었다.

(2) 벡터나 좌표계를 표현하고 있는 기준 좌표계를 변환하기 위해

$R_{ac}=R_{ab}R_{bc}$
$p_a=R_{ab}p_b$
위에 식처럼 기준좌표계를 변환시킬 수 있다.

(3) 벡터나 좌표계를 회전하기 위해

$\hat{w}$를 회전축으로 하여 $\theta$만큼 회전시키는 회전행렬을 다음과 같이 표현할 수 있다.

$\hat{w}=(\hat{w}_1,\hat{w}_2,\hat{w}_3)$에 대해 $R$은 다음과 같다.

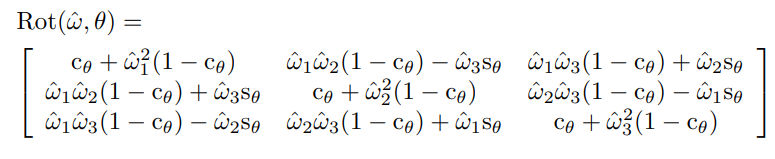
이 식의 증명은 3.2.3.2에서 다룬다.

다음과 같이 {$b$}를 $R$을 이용하여 두 가지 방식으로 회전시킬 수 있다.

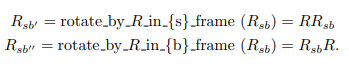
여기서 {$\acute{b}$}는 {$b$}가 회전된 것이다.

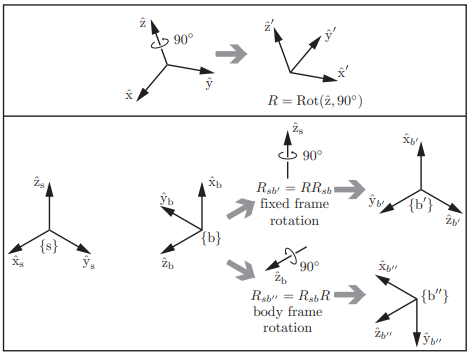
이 식에서 볼 수 있듯이 R을 앞에 곱하면 고정 좌표계에서 표현한 값이 $\hat{w}$인 회전축을 중심으로 회전한 것이고 R을 뒤에 곱하면 물체 좌표계에서 표현한 값이 $\hat{w}$인 회전축을 중심으로 회전한 것이다.
즉 전자는 고정 좌표계를 중심으로 후자는 물체 좌표계를 중심으로 회전시킨 거다.

아래 그림이 이해에 도움이 될 것이다.

벡터의 경우에는 그 벡터를 표현하는 기준 좌표계 하나만 있음으로 벡터의 회전은 다음과 같다.

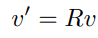
3.2.2 Angular Velocities

각속도

이번에는 좌표계를 임의의 각속도를 중심으로 회전시키는 것을 봐보자
각속도 벡터 $w$는 회전축$\hat{w}$와 각속도의 크기$\dot{\theta}$로 다음과 같이 정의된다.
$w=\hat{w}\dot{\theta}$
다음 그림과 같이 좌표계를 회전시킨다.

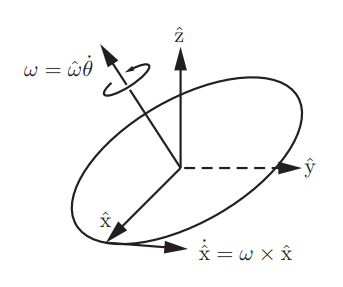
여기서 $w$가 어느 좌표계에서 나타낸 지를 알아야 한다.
$w_s$는 {s}좌표계(고정좌표계)에서 나타낸 것이고 $w_b$는 {b}좌표계(물체좌표계)에서 나타낸 $w$이다.

그리고 위에서 설명한 회전행렬의 활용을 이용하여 다음처럼 기준좌표계를 바꿀 수 있다.

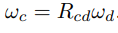
이 각속도는 물체 좌표계{b}의 방향을 표현한 $R$과 다음과 같은 관계가 있다.

여기서 $\dot{R}$은 각속도$w$로 인해 회전하는 $R$의 변화율이고 [$w$]은 $w$의 반대칭(skew-symmetric)행렬표현이다.

이 식의 증명과 반대칭행렬 표현에 대한 설명해보겠다.

이 그림에서 회전하는 좌표계의 단위축들의 변화율은 다음과 같이 구할 수 있다.

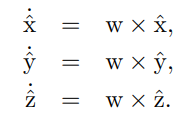
물체 좌표계{b}가 고정 과표계{s}에서 표현된 각속도 $w$를 기준으로 회전한 다고 할 때
단위축 $\hat{x},\hat{y},\hat{z}$는 {b}의 방향을 나타내는 회전행렬을 $R$의 열이다. 이 열을 $r_1,r_2,r_3$로 표현하고 이 회전행렬의 시간에 대한 변화율을 $\dot{R}$로 한다면 다음과 같은 식을 세울 수 있다.

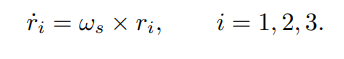
이 세 방정식을 행렬을 사용하여 정리하자

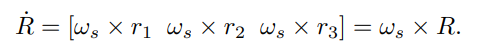
이 식의 외적 기호를 제거하기 위해 우리는 반대칭(skew-symmetric)행렬 표현을 사용할 것이다.

반대칭(skew-symmetric)행렬 표현

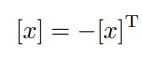
반대칭 행렬이란 위 식을 만족하는 행렬이며
벡터 $x=(x_1,x_2,x_3)^T$의 3 by 3 반대칭 행렬 표현 [$x$]은 다음과 같다.

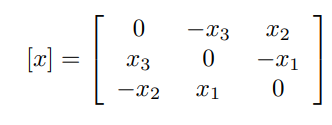
그리고 3 by 3 실수 반대칭행렬의 집합을 $so(3)$라 한다.
반대칭 행렬과 회전회전의 성질로 임의의 $w\in\mathbb{R}^3$와 $R\in SO(3)$가 일을 때 다음 식이 항상 성립한다.

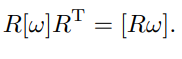
이 식의 증명은 본책에서 볼 수 있다.

이 반대칭행렬 표현을 사용하여 우리는 다음과 같이 위에서 정리한 식의 외적 기호를 없앨 수 있다.

$\dot{R}=w_s\times R=[w_s]R$

이 식의 양변의 오른쪽의 $R^T$을 곱해주면 다음과 같다.

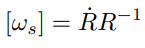
이번에는 {b}를 기준좌표계로 하여 설명해 보자

$w_b$는 회전행렬의 성질로 인해 다음과 같다.

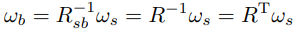
이번에는 반대칭행렬 표현을 이용해보자

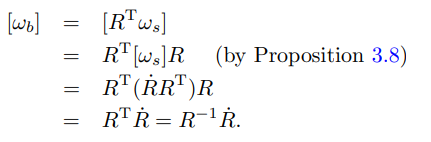
여기서 Proposition 3.8은 위에서 소개되었던 반대칭행렬 표현의 성질인 다음의 식이다.

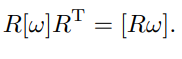
3.2.3 Exponential Coordinate Representation of Rotation

회전의 지수 좌표 표현

회전을 3차원 매개변수로 표현하는 것이 회전의 지수 좌표 표현이다.
3차원의 회전은 회전축 $\hat{w}$와 회전각 $\theta$으로 표현될 수 있고
이 때 벡터 $\hat{w}\theta$가 회전의 3차원 지수좌표 표현이 된다.

회전행렬 $R$의 지수좌표 $\hat{w}\theta$는 다음과 같이 3가지 방식으로 해석될 수 있다.

• 처음 $s$와 일치하던 좌표계가 $s$에서 표현한 축$\hat{w}$를 중심으로 $\theta$만큼 회전했다 할 때 $R$은 회전한 좌표계의 방향을 $s$에서 표현한 것이다.

• 처음 $s$와 일치하던 좌표계가 $s$에서 표현한 각속도 $\hat{w}$$\theta$로 단위 시간 만큼 회전했다 할 때 $R$은 회전한 좌표계의 방향을 $s$에서 표현한 것이다.

• 처음 $s$와 일치하던 좌표계가 $s$에서 표현한 각속도 $\hat{w}$로 시간$\theta$ 만큼 회전했다 할 때 $R$은 회전한 좌표계의 방향을 $s$에서 표현한 것이다.

여기서 회전행렬과 지수좌표 사이에 변환을 행렬지수와 행렬로그 를 활용하여 할 수 있다.

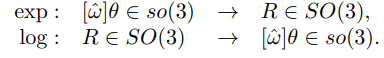
위 표현처럼 지수좌표가 $\hat{w}\theta$일때 반대칭행렬$[\hat{w}]\theta$의 행렬지수(exp)가 그 회전의 회전행렬$R$이고
회전행렬$R$의 행렬로그(log)가 지수좌표의 반대칭행렬$[\hat{w}]\theta$이다.

3.2.3.2 Exponential Coordinates of Rotations

행렬 지수(회전의 지수 좌표)

회전의 지수좌표가 $\hat{w}\theta$일때 회전의 회전행렬 즉 반대칭행렬$[\hat{w}]\theta$의 행렬지수는 다음과 같다.

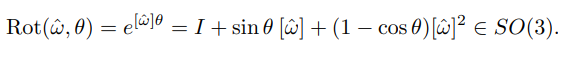
행렬로 표현하면

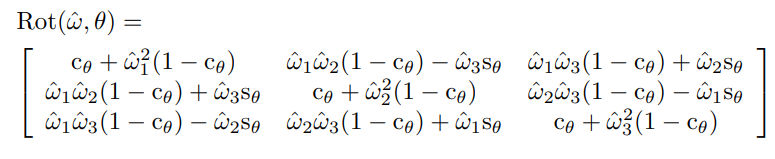
이다.

행렬 지수 표현은 $e^{[\hat{w}]\theta}$로 많이 사용함으로 위에 행렬표현을 암기하기 보다는 $\hat{w}$을 중심으로 $\theta$만큼 회전하는 회전행렬을 $e^{[\hat{w}]\theta}$로 표현한다는 것을 기억하자.

3.2.3.3 Matrix Logarithm of Rotations

행렬 로그(회전 행렬의 행렬 로그)

다음과 같은 알고리듬으로 회전행렬$R$의 행렬지수를 구할 수 있다.

• $R=I$이면 $\theta=0$이고 $\hat{w}$은 정의되지 않는다.

• $trR=-1$이면 $\theta=\pi$이고 $\hat{w}$는 다음 세 벡터 중에서 적합한 해로 둔다.
  
  
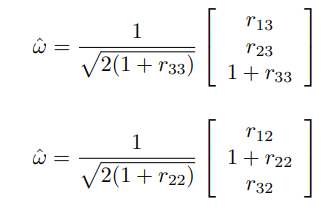
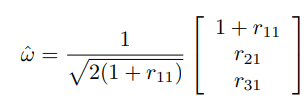
  여기서 $r_{ij}$는 $R$의 $i$행 $j$열인 원소이다.

• 그 외에 경우에는 다음과 같다.
  
  

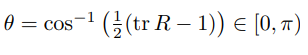
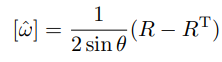
모든 $R$이 알고리금의 세 가지 경우 중 어느 한 가지에 속하기 때문에 모든 행렬 $R$이 존재한다. 즉 지수좌표 $\hat{w}\theta$가 존재한다.
행렬 로그가 계산하는 지수 좌표는 $\Vert \hat{w}\theta \Vert \leq \pi$이기 때문에 벡터 $r$을 $r=\hat{w}\theta$라고 하고 모든 회전행렬의 지수좌표에 대한 벡터 $r$을 3차원 공간에 그린다면 반지름이 $\pi$인 속인 꽉찬 구가 나올 것이다. 즉 $SO(3)$를 이런 구로 표현할 수 있다. 여기서
$trR\neq-1$이면 임의의 $R$에 해당하는 점(벡터) $r$이 유일하게 존재하고
$trR=-1$이면 이 $R$에 해당하는 점 $r$은 구면에 서로 반대편에 존재하는 두 점으로 주어진다. ($\theta=k\pi$에서 $k$가 홀수인 경우를 생각해 보자!)

이런 행렬지수와 행렬로그의 증명은 본책에서 볼 수 있다.

3.3 Rigid-Body Motions and Twists

강체운동과 트위스트

지금 까지 좌표계(강체)의 회전에 대해서만 다루었다. 이번에는 좌표계의 위치까지 다루어 보아 강체의 운동을 설명해볼 것이다.

3.3.1 Homogeneous Transformation Matrices

동차 변환행렬

회전행렬은 강체의 회전만을 표현한다. 이번에는 회전과 위치를 모두 표현하는 동차 변환행렬(homogeneous transformation matrix)에 대해 알아보자

$R$은 {s}에서 바라본 {b}의 방향을 표현하는 회전행렬이고

벡터 $p\in\mathbb{R}^3$는 {s}에서 바라본 {b}의 원점을 열 벡터로 표현한 것일 때

동차 변환행렬 $T$는 다음과 같이 회전행렬 $R$과 벡터 $p$ 를 하나의 행렬로 묶어서 표현하며 {s}에서 바라본 {b}의 자세를 나타낸다.

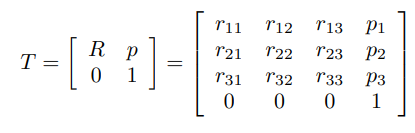
변환행렬 $T$는 ($R,p$)로 표기되기도 한다.

위와 같이 $R\in SO(3)$와 열벡터 $p\in\mathbb{R}^3$로 표현된 행렬들을 특수유클리드군(Special Euclidean Group) $SE(3)$이라고 한다. (강체운동의 군 혹은 동차 변환행렬의 군으로도 알려졌다.)
$SE(2)$은 3 by 3 행렬이고 2차원의 좌표계의 방향과 위치를 표현한다.

3.3.1.1 Properties of Transformation Matrices

변환행렬의 성질
이런 변환행렬의 성질을 알아보자

• 변환행렬의 역행렬 또한 변환행렬이며 다음과 같은 형태를 갖는다.
  

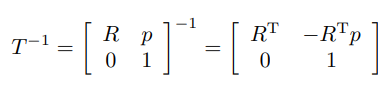
• 두 변환행렬의 곱 또한 변환행렬이다.

• 변환행렬의 곱셈은 결합 법칙을 만족한다.

• 모든 변환행렬 $T\in SE(3)$와 $x,y,z\in \mathbb{R}^3$에 대해 다음이 성립한다.
  (a) $\Vert Tx-Ty\Vert=\Vert x-y\Vert$
  (b) $\langle Tx-Tz,Ty-Tz \rangle=\langle x-z,y-z \rangle$
  이 성질은 변환행렬의 활용을 본 후에 더 봐야 이해가 잘 될 것이다.
  

3.3.1.2 Uses of Transformation Matrices

변환행렬의 활용

변환행렬의 활용 또한 회전행렬의 활용과 비슷한다. 단지 변환행렬은 회전뿐만 아니라 위치까지 다룬다.

변환행렬의 활용을 알아보자

(1) 강체의 자세(위치와 방향)을 표현하기 위해

{s}에서 바라본 물체 좌표계{b}자세를 표현하는 변환행렬을 $T_{sb}$라고 하며
$T_{sb}=(R,p)$에서 $R$은 {s}에서 본{b}의 방향 $q$는 {s}에서 본{b}의 위치를 바타낸다.

(2) 벡터나 좌표계를 표현하고 있는 기준 좌표계를 변환하기 위해

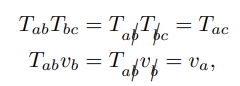
회전행렬 때처럼 위에 식과 같이 기준좌표계를 변환시킬 수 있다.

(3) 벡터나 좌표계를 이동시키기 위해

$T=(R,p)$를 통하여 벡터나 좌표계를 $R$만큼 회전시킨 후 $p$만큼 이동시킬 수 있다.
예를들어 벡터 $x\in\mathbb{R}^3$를 변환시킨다고 한다면 $x$의 아래의 1을 붙여 벡터$(x^T,1)^T$를 만들고 $T=(R,p)$를 통하여 변환해보자.

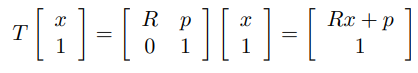
이와 같이 $Rx+p$를 얻을 수 있고 이것은 $x$를 $R$만큼 회전시킨 후 $p$만큼 이동시킨 것이라는 것을 알 수 있다. 여기서 $(x^T,1)^T$은 $x$를 동차 좌표로 표현한 것이고 그래서 $T\in SE(3)$를 동차 변환이라 부르는 것이다.
앞으로 $Tx$처럼 벡터와에 곱은 위와 같은 변환을 의미한다.
이는 좌표계도 똑같이 적용된다.
여기서 회전행렬 때와 같이 변환행렬을 어디에 곱하는 지에 따라 기준좌표가 달라진다.

• $T$를 $T_{sb}$앞에 곱했을 때(고정좌표계 기준의 변환)
  
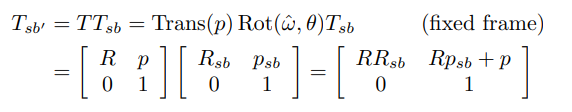
  $T=(R,p)$의 $\hat{w}$와 $p$를 표현한 좌표계가 {s}가 된다. 그리고 이런 고정좌표계 기준의 변화는 좌표계{b}를 {s}좌표계를 기준으로 회전시킨 후 회전된 {b}를 {s}의 $p$만큼 이동시켜 {$b\acute{}$}를 얻는다.

• $T$를 $T_{sb}$뒤에 곱했을 때(물체좌표계 기준의 변환)
  
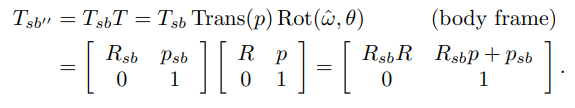
  $T=(R,p)$의 $\hat{w}$와 $p$를 표현한 좌표계가 {b}가 된다. 그리고 이런 물체좌표계 기준의 변화는 좌표계{b}를 {b}의 $p$만큼 이동시킨 후 이동된 좌표계를 기준으로 회전시켜 {$b\acute{}$}를 얻는다.

이런 이동의 차이를 다음 그림에서 시각적으로 볼 수 있다.

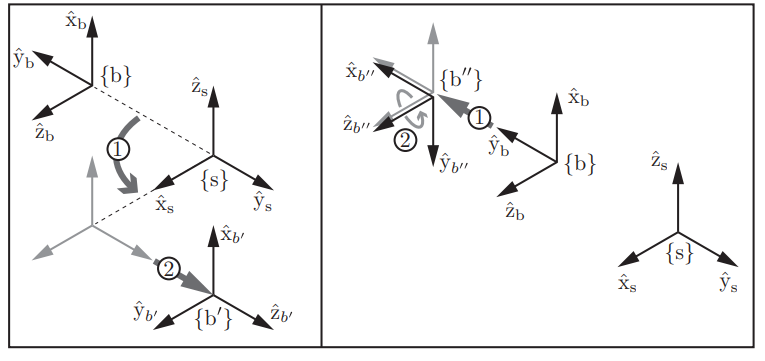
왼쪽 그림이 고정좌표계 기준의 변환이고 오른쪽이 물체좌표계 기준의 변환이다.

3.2.2 Twists

트위스트

변환행렬이 회전과 위치를 모두 표현한 것처럼
트위스트는 위에서 배운 물체의 각속도와 선속도를 다음과 같이 모두 표현한 것이며 공간 속도(spatial velocity)라고도 불린다.

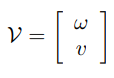
이 트위스트는 $\mathcal{V}$로 표현되며 첨자를 통해 다음과 같이 표현된다.

• $\mathcal{V}_b$: 물체 좌표계에서의 트위스트 즉 물체 트위스트(body twist)
• $\mathcal{V}_s$: 공간(고정) 좌표계에서의 트위스트 즉 공간 트위스트(spatial twist)

고정좌표계{s}와 물체좌표계{b}가 있고 물체 좌표계가 부착된 강체가 각속도 $w$로 회전하면서 속도 $v$로 이동하고 있다고 하자 이때 트위스트 $\mathcal{V}_b$와 $\mathcal{V}_s$는 다음과 같다.

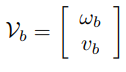
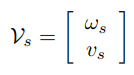
$w_b$는 {b}에서 표현한 각속도이며 $w_s$는 {s}에서 표현한 각속도이다.
$v$는 이 강체가 무한히커서 {s}의 원점 위에도 이 강체가 놓인다고 가정을 하면 다음과 같은 해석이 가능하다.

• $v_b$는 강체에서 {b}의 원점에 있는 점의 선속도를 {b}에서 표현한 값이다.
• $v_s$는 강체에서 {s}의 원점에 있는 점의 선속도를 {s}에서 표현한 값이다.

여기서 조심해야 할 것은 회전의 중심이 {s}의 원점을 지나지 않는다면 $v_s$은 강체 중심의 선속도와 동일하지 않다는 것이다.
다음 그림과 같이 강체 중심이 아닌 {s}의 원점에 있는 점의 선속도를 {s}에서 표현한 것 임으로 강체가 이동하지 않고 회전만 해도 $v_s$는 0이 아니게 된다.
($v_b$에서도 마찬가지이다.)

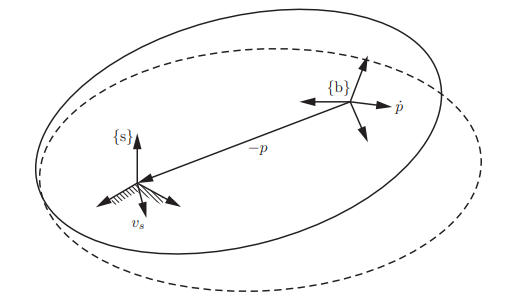
(초기 강체의 자세가 실선이고 이동후의 강체의 자세가 점선이다.)
이때 $v_s$는 다음과 같다.

$v_s=-w\times q$

그리고 {s}에서 바라본 {b}의 자세인 변환행렬$T_{sb}$가 있을 때 트위스트와 변환행렬은 다음과 같은 관계가 있다.

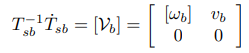
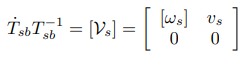
여기서 [$\mathcal{V}$]는 4 by 4행렬이며 트위스트의 행렬표현 $se(3)$라 한다.
위에 식들은 각속도 파트에서 다룬 각속도-회전행렬의 관계와 비슷한 것을 알 수 있다.

좌표계{c},{d}가 있을 때 트위스트 $\mathcal{V}_c$,$\mathcal{V}_d$또한 다음과 같이 서로 변환이 가능하다.

여기서 [$Ad_{T}$]는 주어진 $T$에 대한 수반 표현이며 $T=(R,p)$에 대해 다음과 같다.

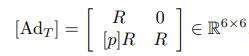
이 수반표현은 다음과 같이 표현하기도 하며

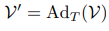
다음과 같은 성질을 가진다.

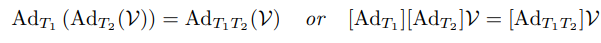
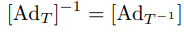
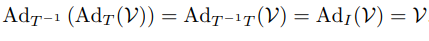
이와 같은 트위스트에 관한 식들은 행렬곱을 통해 직접 증명이 가능하며 그 과정은 본책에서 볼 수 있다.

3.3.2.2 The Screw Interpretation of a Twist

트위스트의 스크류 해석

각속도$w$는 회전축 $\hat{w}$와 각속력$\dot{\theta}$을 이용해 $w=\hat{w}\dot{\theta}$로 표현되 듯이 트위스트$\mathcal{V}$도 스크류 축$\mathcal{S}$와 이에 대한 각속력 $\dot{\theta}$를 이용하여 $\mathcal{V}=\mathcal{S}\dot{\theta}$으로 표현된다.
즉 스크류 축은 회전운동의 회전축과 대응대며 회전축에서 이동 정보까지 담은 것이며 스크류 운동은 어떠한 축을 중심으로 회전하면서 그 축을 따라 이동하는 운동을 말한다.

스크류 축의 이해를 돕기위해 스크류 축을 {$q,\hat{s},h$}으로 표현해 보겠다.

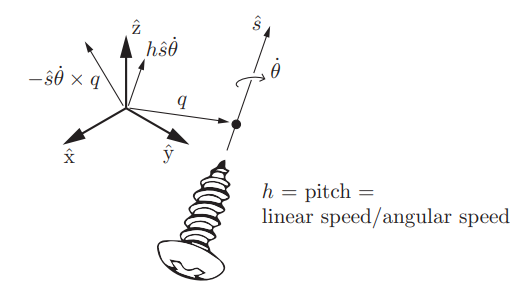
위 그림처럼 $q\in\mathbb{R}^3$은 축 위의 임의의 점, $\hat{s}$는 축 방향을 나타내는 단위벡터,$h$는 스크류 피치(screw pitch)이다. 스크류 피치는 스크류 축을 따라 이동하는 석속력과 스크류 축에 대한 회전 속력 $\dot{\theta}$의 비율이다.(순수한 회전의 경우 $h$=0, 순수한 병진운동의 경우에는 $h$는 무한대로 발산한다.)

위 그림에서 스크류 축 $\mathcal{S}$와 각속력 $\dot{\theta}$에 대한 트위스트 $\mathcal{V}$는 다음과 같다.

스크류 축의 {$q,\hat{s},h$}표현은 번거롭기 때문에 이러한 트위스트를 정규화 하여 다음과 같이 표현한다.

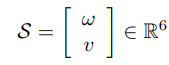
스크류 축의 $v$도 트위스트 때와 비슷하게 해석된다.(차이점은 스크류 축의 경우는 크기를 제외한 방향만을 나타낸다.)
(트위스트, 스크류 축 모두 $(w,v)$를 사용하기 때문에 맥락을 보고 둘 중에 무엇인지 파악한다.)
여기서 $w$는 스크류 운동의 회전축을 의미한다 그럼으로 $\Vert w \Vert=1$ 혹은 $\Vert w \Vert=0$를 만족한다.

• $\Vert w \Vert=1$이라는 것은 스크류 운동에서 회전이 존재한다는 뜻이며 $v$는 회전운동과 병진운동에 의한 속도의 합인 $v=-w\times q+hw$이다.
• $\Vert w \Vert=0$이라는 것은 스크류 운동에서 회전이 없다는 뜻이다. 즉 순수한 병진운동이다. 이 경우에 $v$는 병진운동의 방향만을 나타내고 $\Vert v \Vert=1$이다.

스크류 축은 단순히 정규화된 트위스트이기 때문에 스크류 축 $\mathcal{S}=(w,v)$의 4 by 4행렬 표현 $[\mathcal{S}]$은 다음과 같다.

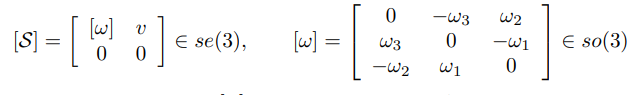
또한 스크류 축의 기준좌표계 변환도 다음과 같이 트위스트의 경우와 같다.

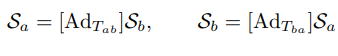
3.3.3 Exponential Coordinate Representation of Rigid-Body Motions

강체 운동의 지수 좌표 표현

샤를-모치 이론(chasles-mozzi theorem)에 따르면 모든 강체 이동은 공간상에 고정된 스크류 축 $\mathcal{S}$에 대한 이동으로 나타낼 수 있다.
그럼으로 회전의 지수좌표 $\hat{w}\theta$처럼 동차 변환$T$의 6차원 지수 좌표를 $\mathcal{S}\theta$로 정의할 수 있다.
여기서 $\mathcal{S}$는 스크류 축이고 $\theta$는 이동의 변위량을 의미한다.
즉 스크류 운동의 회전이 존재한다면 즉 $\Vert w \Vert=1$이면 $\theta$는 이 회전의 회전각을 의미하고
스크류 운동이 회전이 없는 순수한 병진운동이라면 $\theta$는 스크류 축을 따라 이동한 선형 거리가 된다.
그리고 회전의 경우와 유사하게 다음처럼 행렬지수(exp)와 행렬(log)로그를 다음과 같이 정의할 수 있다.

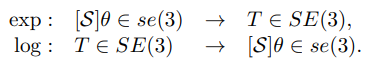
3.3.3.1 Exponential Coordinates of Rigid-Body Motions

강체 운동의 지수 좌표

스크류 축 $\mathcal{S}=(w,s)$와 변위량 $\theta$에서

• $\Vert w \Vert=1$이면 행렬지수는 다음과 같다.
  
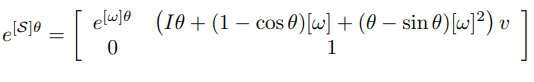
• $\Vert w \Vert=0$,$\Vert v\Vert=1$이면 행렬지수는 다음과 같다.
  

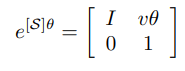
3.3.3.2 Matrix Logarithm of Rigid-Body Motions

강체 운동의 행렬 로그

주어진 $T=(R,q)\in SE(3)$의 행렬로그 $[S]\theta\in se(3)$는 다음의 알고리듬으로 구해진다. ($S=(w,v)$라고 하자)

• $R=I$인 경우: $w=0, v=p/\Vert p\Vert, \theta=\Vert p\Vert$이다.
• $R\neq I$인 경우: ($SO(3)$알고리듬에서 $\hat{w}$라고 표기한) $w$와 $\theta$를 $SO(3)$에서 $R$의 행렬로그를 통해 구한다.
  그리고 $v$는 다음과 같이 구한다.
  
  
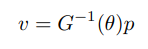
  이 식들의 유도는 본 책에서 볼 수 있다.

3.4 Wrenches

렌치
렌치(wrench)는 강체에 힘이 가해졌을 때 그때 발생한 모멘트와 그 힘을 같이 나타낸 것이다.
{a}좌표계에서 표현된 강체 위의 점 $r_a\in\mathbb{R}^3$에 힘$f_a\in\mathbb{R}^3$가 가해지고 있다고 하자 이때 힘은 토크 또는 모멘트를 발생시키는데 {a}에서 표현한 모멘트인 $m_a\in\mathbb{R}^3$를 다음과 같이 표현할 수 있다.

트위스트 때와 비슷하게 모멘트와 힘을 묶어 다음과 같이 렌치(wrench)$\mathcal{F}_a$를 다음과 같이 쓸 수 있다.

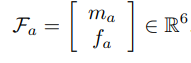
6차원 벡터 공간 힘(spatial force)라고도 부른다.
힘 성분 없이 모멘트만 있는 렌치는 순수 모멘트(pure moment)라고 한다.

두 개 이상의 렌치가 강체의 적용하고 있을 때 모든 렌치가 같은 좌표계에서 표현되고 있다면 최종 렌치는 각각의 렌치의 벡터합이 된다.

이러한 렌치도 트위스트와 스크류 축 처럼 다음과 같이 기준좌표계의 변환이 가능하다.

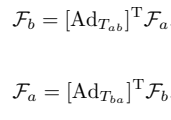
이 기준좌표의 변환은 트위스트와 스크류 축의 변환과 같은 방식으로 증명 될 수 있다. 하지만 렌치의 경우에는 이 외에 $\mathcal{F}_a$와 $\mathcal{F}_b$사이에 관계를 직관적으로 유도할 수 있는 방법이 있는데 이 과정이 물리적으로 의미가 있기 때문에 이번에는 스킵을 하지 않고 증명을 해보겠다.

기준 좌표계가 변해도 일률의 값은 변하지 않는다. 일률은 속도와 힘의 내적으로 구할 수 있기 때문에 다음식이 만족한다는 것을 알 수 있다.

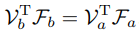
이 식에 $\mathcal{V}_a=[Ad_{T_{ab}}]\mathcal{V}_b$를 대입하면 다음과 같이 정리 할 수 있다.

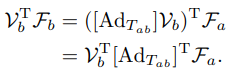
일반적으로 고정된 좌표계{S}와 물체 좌표계{b}를 사용할때 공간 렌치(spatial wrench)$\mathcal{F}_s$와 물체 렌치(body wrench)$\mathcal{F}_b$로 표현한다.