Dijkstra Algorithm - ShortestPath

과제 03번 ADT

• 수업시간에 배운 다익스트라 알고리즘을 사용하여 최단거리 경로를 구하는 문제이다.
• 강의에선 C++ STL의 std::priority_queue를 쓰는 방법으로 예시를 들어주셨지만 priority_queue<pair<distance,vertex>>에서 임의의 pair의 distance를 수정, 수정 후 정렬하는 메소드를 제공하지 않아 이를 모두 구현해야하는 불편함이 있었다.(일일이 pop하여 temp에 저장하고 다시 추가해줘야한다..
  (하지만 O(n^2) -> O(nlogn)으로 개선된 시간복잡도를 보인다.)
• 난 STL의 std::vector를 사용해 checked[]과 distance[]를 사용하여 (cloud에 새로 들어갈) 가장 가까운 정점을 그때마다 찾아주는 방식으로 구현하였다.
  (O(n^2)의 시간복잡도를 보인다)
• 각 정점 별 최단 경로를 저장하기 위해 vector<vector<queue<int>>> path를 사용하였다. queue를 통해 각 정점별 경로를 추가하고 출력할 수 있다.

---

Graph 클래스에서 사용한 field 변수들

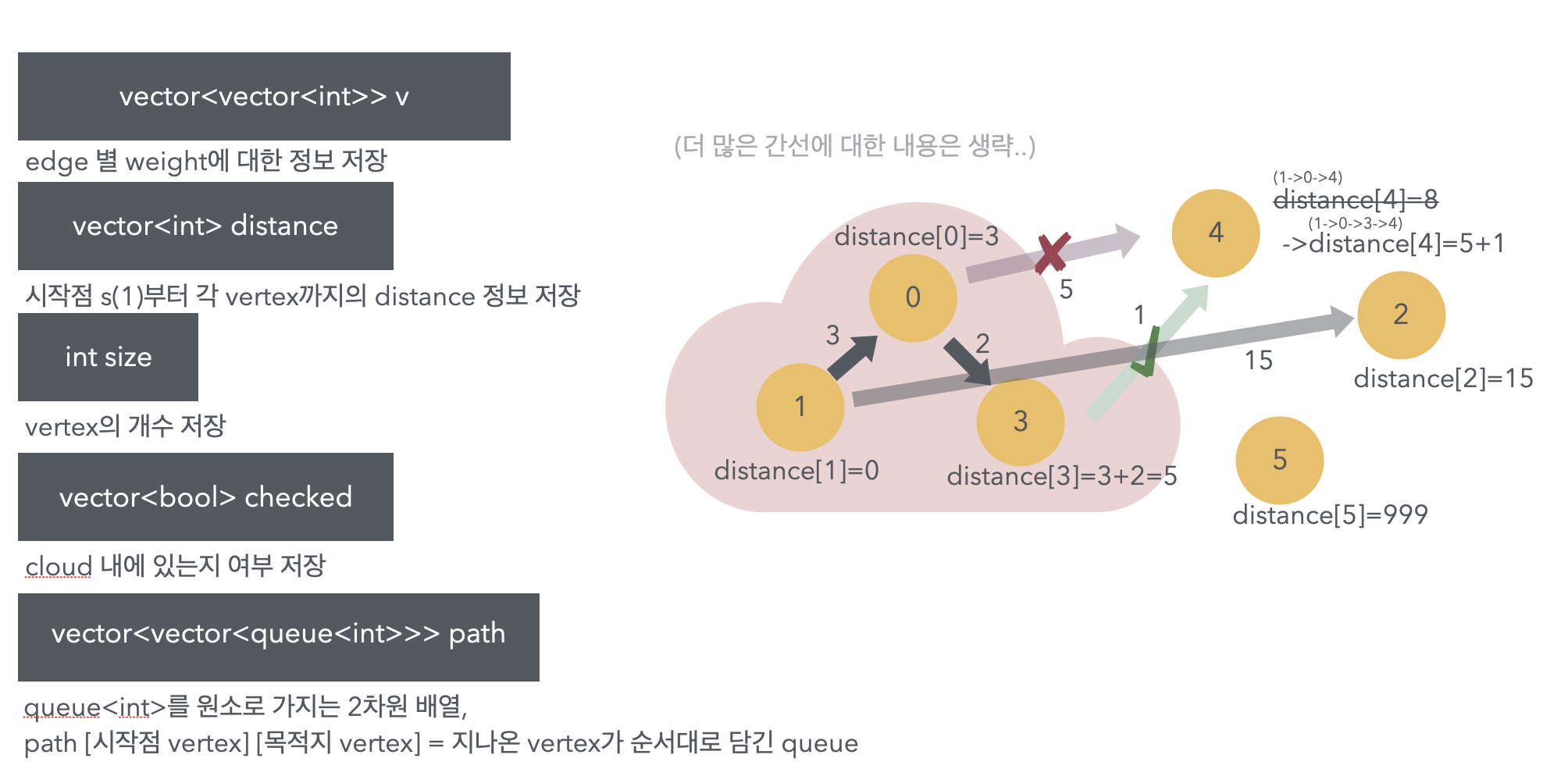
vector<vector<int>> v;// weight 행렬
vector<int> distance; // 현재 vertex별 거리 배열
int size;// vertex 개수
vector<bool> checked; // vertex cloud 판별 배열
vector<vector<queue<int>>> path; // [시작점(size)][각 정점별(size)][경로]

Solution Visualization

Code

graph.h

#include <vector>
#include <queue>
using namespace std;

class Graph {
public :
  void LoadMatrix(string& filename);
  void PrintMatrix();
  int GetSize();
  void PrintShortestPathWeight(int s);
  void PrintShortestPath(int s);
  void FindPath(int s);
private :
  vector<vector<int>> v; // weight 행렬
  vector<int> distance; // 현재 vertex별 거리 배열
  int size; // vertex 개수
  vector<bool> checked; // vertex cloud 판별 배열
  vector<vector<queue<int>>> path; // [시작점(size)][각 정점별(size)][경로]
};

graph.cpp

#include "graph.h"
#include <fstream>
#include <string>
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

void Graph::LoadMatrix(string &filename) {
  ifstream file(filename);
  file >> size;
  v.resize(size, vector<int>(size));
  distance.resize(size, 999); // 최단 거리를 999로 초기화
  checked.resize(size, false); // 방문 여부를 false로 초기화
  path.resize(size, vector<queue<int>>(size));
  for (int i = 0; i < size; i++) {
      for (int j = 0; j < size; j++) {
          file >> v[i][j];
      }
  }
  file.close();
}

void Graph::PrintMatrix() {
  for(int i=0; i<size; i++){
      for(int j=0; j<size; j++){
          cout << v[i][j] << " ";
      }
      cout << endl;
  }
}

int Graph::GetSize() {
  return size;
}

void Graph::PrintShortestPathWeight(int s) {
  FindPath(s);
  // 모든 정점까지의 최단 경로의 가중치의 합을 출력
  int sum = 0;
  for(int i = 0; i < size; i++) {
      sum += distance[i];
  }
  cout << sum;
}

void Graph::PrintShortestPath(int s) {
  FindPath(s);
  for(int i = 0; i < size; i++) {
      queue<int> temp = path[s][i];
      if(i!=s) {
          cout << s << " ";
          while (!temp.empty()) {
              cout << temp.front() << " ";
              temp.pop();
          }
          cout << endl;
      }
  }
}

void Graph::FindPath(int s){
  distance[s] = 0; // 시작 정점까지의 거리를 0으로 설정

  for(int count = 0; count < size - 1; count++) {
      int minDistance = 999, minIndex;

      // 아직 처리되지 않은 정점 중 최단 거리를 찾음
      for(int i = 0; i < size; i++) {
          if(!checked[i] && distance[i] <= minDistance) {
              minDistance = distance[i];
              minIndex = i;
          }
      }
      checked[minIndex] = true;

      // 최단 거리를 갱신하고 경로를 업데이트함
      for(int i = 0; i < size; i++) {
          if(!checked[i] && v[minIndex][i] != 999 && distance[minIndex] + v[minIndex][i] < distance[i]) {
              distance[i] = distance[minIndex] + v[minIndex][i];
              path[s][i] = path[s][minIndex]; // 경로 업데이트
              path[s][i].push(i);
          }
      }
  }
}