워드 임베딩에 대해서 공부를 하면 자주 등장하는 임베딩 기법으로 GloVe가 등장한다. Word2Vec과 함께 실제로도 가장 많이 사용되며 성능 차이도 거의 없으나 Word2Vec에 비해 개념 자체가 어려워 설명 없이 넘어가는 경우가 많다.
본인도 이번 기회에 정리를 해보며 GloVe 임베딩 방법론에 대해 공부해보고자 한다.
🐣 1. 등장 배경
GloVe가 등장하기 이전까지 사용되던 임베딩 방식은 대표적으로 LSA와 Word2Vec 방식이 있다.
LSA의 경우 문서 전체의 각 단어의 빈도수를 담은 행렬이라는 전체적인 통계 정보를 입력으로 받아 차원을 축소(Truncated SVD)하여 잠재된 의미를 끌어내는 방법론이다. 즉, 각 단어의 유사성이나 관계성보다는 문서 전체에 단어가 등장하는 빈도를 통해 단어들을 임베딩하고자 했다.

반면, Word2Vec은 window를 사용해 문서 전체가 아니라 중심단어를 둘러싼 주변단어의 실제값과 예측값에 대한 오차를 손실 함수를 통해 줄여나가며 학습하는 예측 기반의 방법론이다.
이 둘은 각각 장단점이 있는데 LSA는 카운트 기반으로 코퍼스의 전체적인 통계 정보를 고려하기는 하지만 단어 의미의 유추 작업(Analogy task)에는 성능이 떨어진다. 즉, 임베딩된 단어의 선형대수적 연산 능력이 매우 떨어져 단어간의 관계성 부분을 고려하지 못한다.
Word2Vec는 예측 기반으로 단어 간 유추 작업에는 LSA보다 뛰어나지만, 임베딩 벡터가 윈도우 크기 내에서만 주변 단어를 고려하기 때문에 코퍼스의 전체적인 통계 정보를 반영하지 못한다.
GloVe는 이러한 점을 지적하며 각 임베딩의 방식을 부분적으로 차용하며 등장한 방식이다.
GloVe 논문에서는 임베딩된 두 단어벡터의 내적이 말뭉치 전체에서의 동시 등장확률 로그값이 되도록 목적함수를 정의했다. 그렇게 설정한 이유는 단어 임베딩의 선형성(내적)을 내포한 채로 문서 전체의 통계치를 반영하고자 했기 때문이다.
their dot product equals the logarithm of the words’ probability of co-occurrence
“임베딩된 단어벡터 간 유사도 측정을 수월하게 하면서도 말뭉치 전체의 통계 정보를 좀 더 잘 반영해보자”가 GloVe가 지향하는 핵심 목표다.
🛠 2. Window based Co-occurrence Matrix(윈도우 기반 동시발생 행렬)와 Co-occurrence Probability(동시 등장 확률)
동시발생 행렬
단어의 동시 발생 행렬의 행과 열을 전체 단어 집합의 단어들로 구성된다. 중심단어 i의 주변으로 window size 내에서 주변 단어 k가 등장한 횟수를 i행 k열에 기재한 행렬을 말합니다. 그리고 이를 대칭행렬로 만들어주면 된다.
윈도우 크기가 1이고, 주어진 텍스트가 아래와 같을 때 구성한 동시 발생 행렬은 그 아래의 표와 같다.
- I like deep learning
- I like NLP
- I enjoy flying
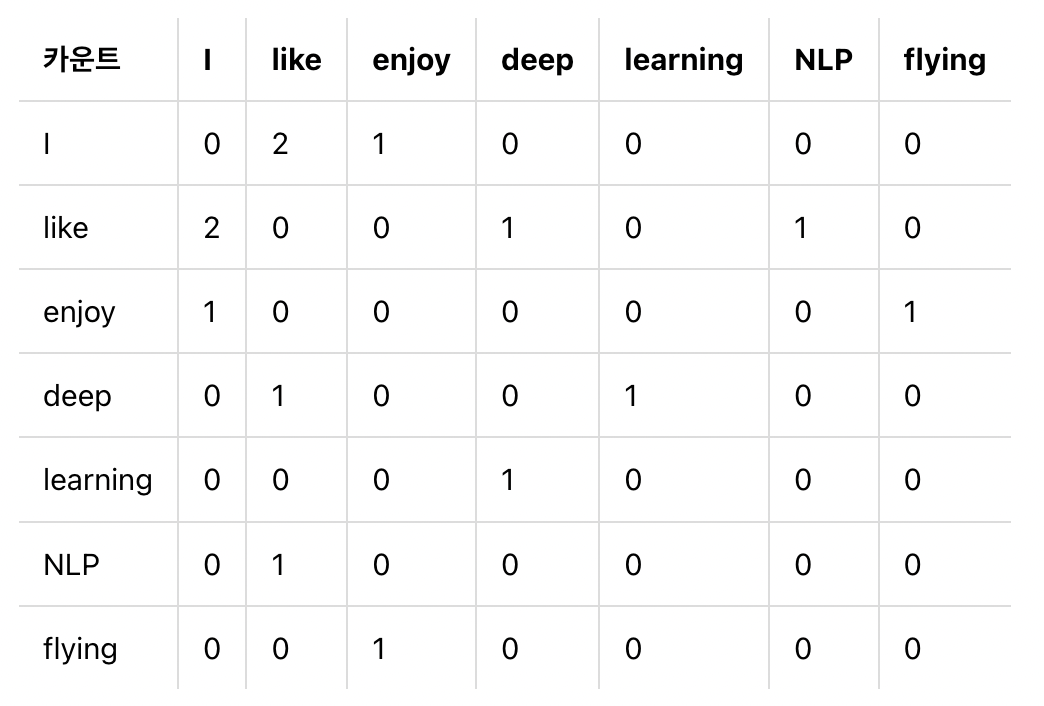
- 해당 내용은 스탠포드 대학교의 자연어 처리 강의에 나온 내용을 바탕으로 구성되었다.
동시 등장 확률
동시 등장 확률은 쉽게 말하면 두 단어가 등장할 조건부 확률이다. 즉, 특정 단어 i의 전체 등장 횟수를 카운트하고, 특정 단어 i가 등장했을 때 어떤 단어 k가 등장한 횟수를 카운트하여 계산한 조건부 확률 이다. 이때, i는 중심단어 k는 주변단어로 볼 수 있다.
동시 등장 행렬로 파악하면, 중심 단어 i의 행의 모든 값을 더한 값을 분모로 하고 i행 k열의 값을 분자로 한 값이다.
다음은 GloVe의 제안 논문에서 등장한 동시 등장 확률을 표로 정리한 하나의 예시이다.
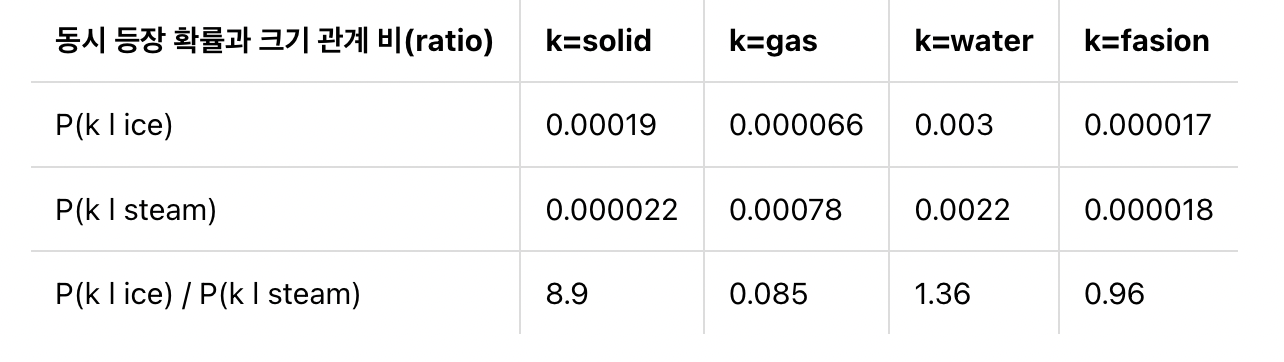
표를 보면 유사한 단어일 수록 동시 등장 확률이 크고 그렇지 않을 수록 작다. 위의 표에 따르면 ice라는 단어가 주어졌을 때 solid가 등장할 확률은 steam이 주어졌을 때 solid가 나타날 확률보다 높다. 이는 단어의 연관성으로 보았을 때 자명하다.
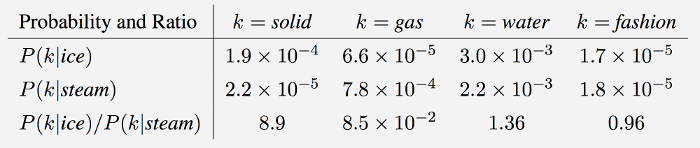
이때, 은 1보다 훨씬 큰 값(8.9)을 가진다. 반대로 은 1보다 훨씬 작은 값(0.0085)이 나오고 ice, steam과 관련성이 높거나 별로 없는 water와 fashion은 모두 1 안팎의 값이 나온다.
GloVe 연구팀은 특정 중심 단어가 주어졌을 때 임베딩된 두 단어벡터의 내적이 두 단어의 동시등장확률 간 비율이 되게끔 임베딩하려고 했다. 즉, 중심단어로 어떤 것이 주어지냐에 따라 단어 간의 내적값이 달라지도록 만드는 것이다.
이때 문서를 임베딩하면 중심단어로는 문서 전체의 모든 단어가 설정되므로 최종적으로 문서 전체를 반영하면서도 유사도를 반영한 임베딩 방법론을 구성하고자 한 것이다.
그렇기 위해서는 임베딩된 단어들 간의 내적값들이 문서 전체 단어의 분포를 바탕으로 알맞게 조절되어야 한다.
🔥 3. GloVe의 손실함수(목적함수)
주의. 여기서부터 갑자기 난이도가 급상승합니다.
문서에서 사용하는 notation은 다음과 같다.

우선 각 단어들의 임베딩으로 나타난 결과들의 내적값은 문서 전체에서의 동시 등장 확률이 되어야 한다.

위의 수식을 손실함수로 사용할 수 없으므로 임베딩된 벡터의 특성을 잘 반영하는 손실함수를 만들어주어야 한다.
이를 위해서는 임베딩된 단어 벡터들을 통해 문서 전체의 단어들간의 동시 발생 확률 비율을 구하는 목적함수로 학습하고자 한다. 그리고 그것을 만족시켜주는 함수 F가 있다고 가정한다.
여기서 비율을 사용하는 이유는 개인적으로 차이가 float16으로 표현이 되기 때문이라고 생각한다.
그렇지 않고 그대로 사용하면 너무 작은 값이 사용된다.
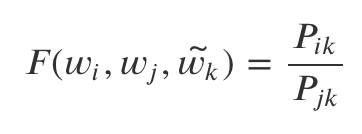
우리는 두 개의 중심단어가 주어지고 하나의 주변단어가 주어질 때 어떠한 함수 F를 통해 동시 발생 확률 비율을 도출할 수 있어야 한다.
그래야 문서 전체 내용을 담을 수 있으므로
우선 𝐹 안에 집어넣을 간에 관계를 따져보기 위해 와 를 뺀 벡터에 를 내적한다.
논문에서는 함수 는 두 단어 사이의 동시 등장 확률의 크기 관계 비(ratio) 정보를 벡터 공간에 적절하게 인코딩하는 것이 목적이다.
이를 위해 GloVe 연구진들은 와 라는 두 벡터의 차이를 함수 의 입력으로 사용하는 것을 제안한다.
사실 이렇게 빼게 되면 추후에 Homomorphism이 성립이 되어 손쉽게 처리할 수 있기 때문이다.
또 그냥 그렇게 하면 나중에 log 변환으로 -를 /으로 손쉽게 교체할 수 있기 때문인 것 같다.
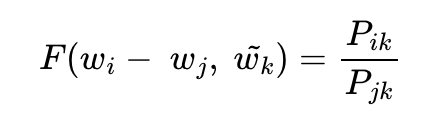
우변과 좌편이 스칼라, 벡터로 다르므로 이를 맞춰주기 위해서 함수 의 두 입력에 내적(Dot product)을 수행한다.
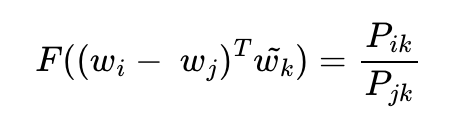
이때, 함수 F가 만족해야 할 필수 조건이 있다.
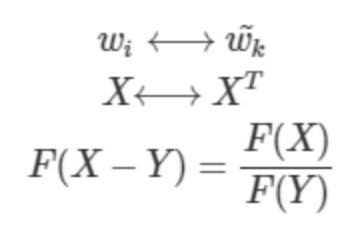
-
중심 단어 와 주변 단어에는 모든 단어가 올 수 있으므로 서로 변동이 가능해야 한다.
-
두번째로 X는 당연히 대칭행렬이어야 한다.
이것이 성립되게 하기 위해서 GloVe 연구진은 함수 F가 실수의 덧셈과 양수의 곱셈에 대해서 준동형(Homomorphism)을 만족하도록 만들어주었다.
더 공부하고 싶다면, https://dimenchoi.tistory.com/23
식으로 나타내면 아래와 같다.
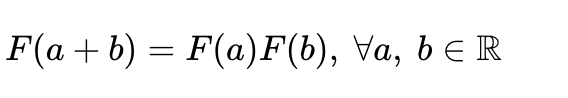
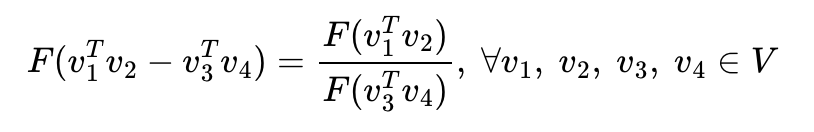
이때 우변이 정리되었으므로 우리가 구하고자 하는 원래 식을 가져와서 다시 식을 정리한다.
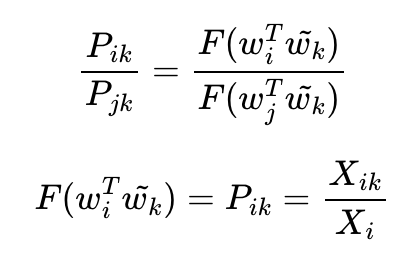
좌변을 다시 풀어서 작성하면 아래의 식으로 정리된다.
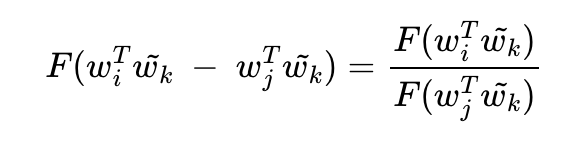
이러한 조건을 만족하는 손쉬운 함수는 지수함수이기 때문에 𝐹를 𝑒𝑥𝑝로 치환하고 식을 정리하면 아래와 같다.
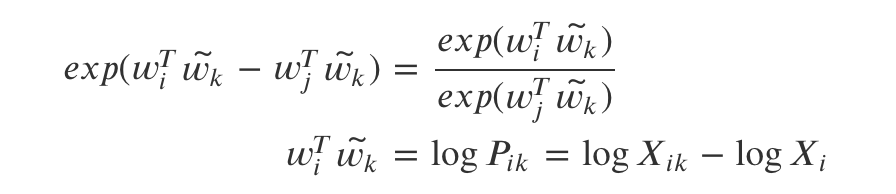
하지만 위의 수식은 첫번째 조건이었던 단어 간의 교체가 불가능하다. 이렇게 되려면 위 식 마지막의 가 와 같아야 한다.
이를 풀어쓰면 각각 가 되어서 당연히 식이 서로 달라지게 된다. 그러나 수식적으로는 달라도 동일하게 평가되어야 한다.
이 때문에 이 부분을 아래와 같이 상수항()으로 처리해 식을 한번 더 변환한다. 이렇게 하면 bias처럼 상수항으로 볼 수 있으므로 둘을 동일한 수식으로 판단할 수 있다.
다만 word가 달라지게 되면 bias도 달라지는 그냥 i와 k에 따라 달라지는 상수항이라고 생각
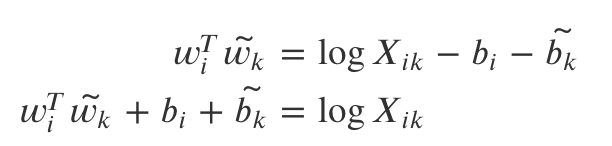
위 식에서 학습되어야 하는 임베딩된 단어들이 좌변으로 몰려 있고, 우변에는 𝑙𝑜𝑔(𝑋𝑖𝑘)를 통해 윈도우 사이즈를 두고 말뭉치 전체에서 단어별 등장 빈도를 구한 co-occurrence matrix에 로그를 취해준 행렬이 있다.
이를 우리가 구하고자 하는 목적함수 J로 나타내면 아래와 같다.
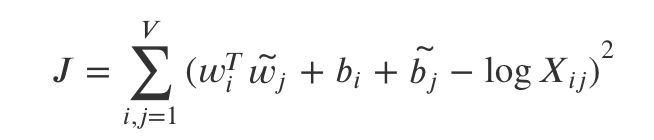
여기서 마지막으로 변환을 한 번 더 해주게 된다.
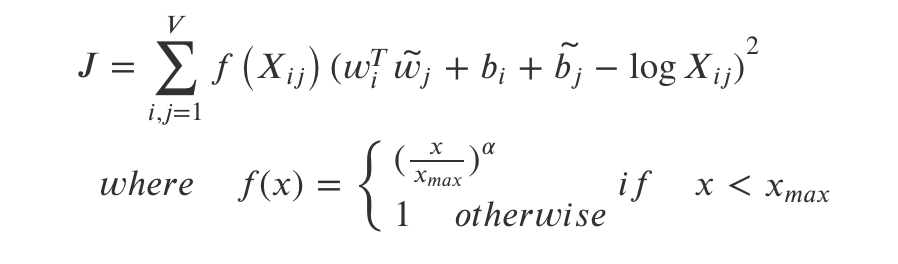
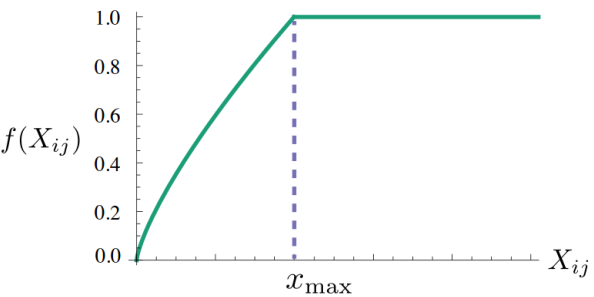
이는 너무 높은 단어 pair의 등장으로 임베딩 결과가 왜곡되지 않게 하기 위함이다. 예를 들어, "it is"라는 단어는 의미가 크지 않지만 당연히 많이 등장할 수 밖에 없으므로 임베딩 결과를 왜곡할 수 있다. 그래서 아래와 같은 f(x)를 추가해주게 된다.
✏️ 4. 후기
GloVe가 문서 전체 통계를 조금 더 반영한 임베딩 기법이라고만 알았지 이렇게 딥하게 공부해본 것은 처음이라 조금 어려웠다. 논문을 2회 읽으며 리뷰를 정리했는데 많이 정리되는 느낌이 들었다.
참조 : https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/09/glove/
