Building Deep Neural Network : step_by_step.ver

Packages

import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases import *
from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward
from public_tests import *

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

np.random.seed(1)

Outline

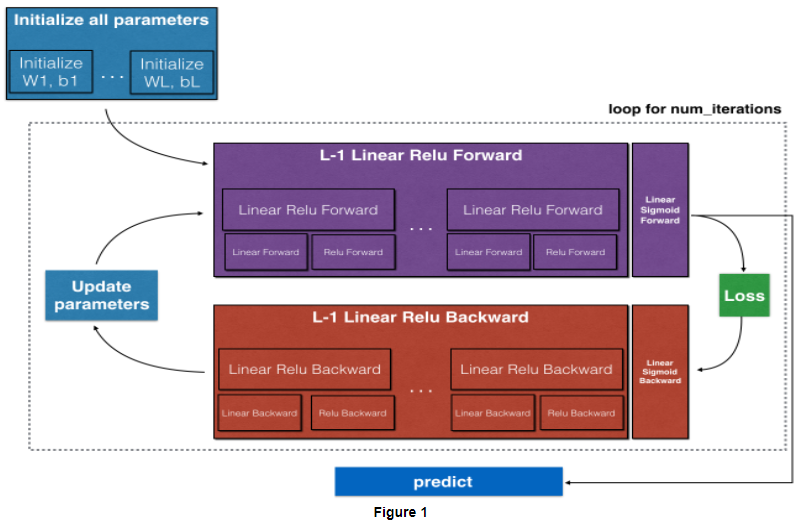
대략적인 순서를 적어보자면,
처음에 parameters을 초기화 해 준 다음, ReLU Forward->Sigmoid Forward에 넣고 Loss를 계산해 준 후, Backward에 넣어서 learning_rate값과 함께 parameters을 업데이트 해 준다. 위 과정을 반복한 후 마지막으로 predict를 한다.

처음 단계로, parameters를 초기화 해 주자.

Initialization

저번 글에서도 했었던 2-layer에서의 parameter초기화와 Deep Neural Network에서의 초기화가 어떻게 다른지 실펴보도록 하겠다.

2-layer Neural Network

def initialize_parameters(n_x, n_h, n_y):
	W1 = np.random.randn(n_h, n_x)*0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h)*0.01
    b2 = np.zeros((n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
                  
    return parameters

parameters = initialize_parameters(3,2,1)를 실행했을 때

라는 결과가 나오게 된다.
이제는 L-layer에서의 parameters을 초기화 해 보자.

L-layer Neural Network

원래는
LINEAR -> RELU -> LINEAR -> SIGMOID
였던 structure가 이제는
[LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID
로바뀌었다는 점에 주의하자.

def initialize_parameters_deep(layer_dims):
    np.random.seed(3)
    parameters = {}
    L = len(layer_dims)
    
    for l in range(1,L):
        parameters['W'+str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])*0.01
        parameters['b'+str(l)] = np.zeros((layer_dims[l], 1))
        
        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l - 1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
        
    return parameters

제일 먼저 보이는 차이점은 for loop을 썼다는 것이다.
그리고 Layer L에서 W의shape은 (nL, nL-1)이므로 두 차원을 초기화시켜줘야 한다.

Forward Propagation Module

Linear Forward

이제 우리는 forward propagation 모델을 만들 수 있다. 아래 수식을 참고하여 가장 기본적인 Linear forward부터 다시 만들어보자.

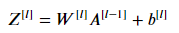
def linear_forward(A, W, b):
    Z = np.dot(W, A) + b
    
    cache = (A, W, b)
    
    return Z, cache

Linear-Activation Forward

sigmoid activation func 는 A, activation_cache = sigmoid(Z)
ReLU activation func는 A, activation_cache = relu(Z) 로 나타낼 수 있다.

def linear_activation_forward(A_prev, W, b, activation):

    if activation == "sigmoid":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)
        
    elif activation == "relu":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)
        
    cache = (linear_cache, activation_cache)

    return A, cache

L-layer Model

이제 마지막으로 L-layer Neural Net을 도입시켜보자.

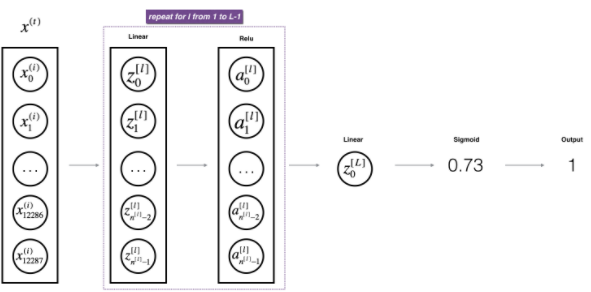
우리는 linear_activation_forwardwith ReLU를 (L-1)번, Sigmoid를 1번 하는 함수를 만들어 줄 것이다.

def L_model_forward(X, parameters):
    caches = []
    A = X
    L = len(parameters) // 2      #number of layers
    
    for l in range(1, L):
        A_prev = A 
        
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation="relu")
        caches.append(cache)
        
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation="sigmoid")
    caches.append(cache)
    
    return AL, caches

간단하게 구현할 수 있다. 또한 caches안에 모든 cache들을 track할 수 있게 되었다. 이제 Cost function을 구해보자!

Cost Function

이전 글에서도 구했듯이 위 식을 구현해내면 된다.

def compute_cost(AL, Y):
    m = Y.shape[1]
    
    logprobs = np.multiply(np.log(AL),Y)+np.multiply((1-Y), np.log(1-AL))
    cost = -1/m*np.sum(logprobs)
    
    cost = np.squeeze(cost)
    
    return cost

Backward Propagation Module

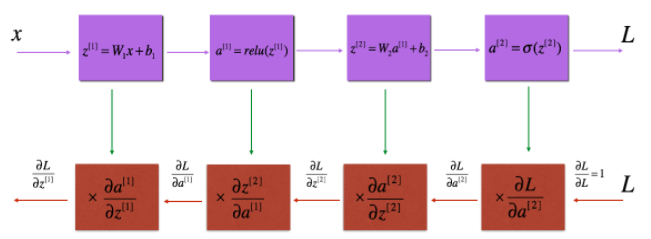
이제 forward와 비슷하게 반대로 미분을 구하는 backward propagation을 만들어보자.
여기서 해야 할 일은 세 가지로 나뉜다.

• linear backward
• LINEAR -> ACTIVATION backward (ReLU & sigmoid)
• [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID backward

혹시 axis=1, axis=0, keepdims 에 대해 헷갈린다면, 이 링크를 참고하길 바란다.

Linear Backward

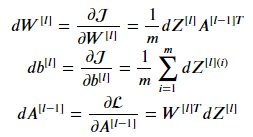
고대로 옮겨주자.

def linear_backward(dZ, cache):
    A_prev, W, b = cache
    m = A_prev.shape[1]
    
    dW = 1/m * np.dot(dZ, A_prev.T)
    db = 1/m * np.sum(dZ, axis=1, keepdims=True)
    dA_prev = np.dot(W.T, dZ)
    
    return dA_prev, dW, db

Linear activation backward

sigmoid backward는 dZ = sigmoid_backward(dA, activation_cache)
relu backward는 dZ = relu_backward(dA, activation_cache)를 참고하자.

def linear_activation_backward(dA, cache, activation):
    linear_cache, activation_cache = cache
    
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
        
    return dA_prev, dW, db

L-model Backward

마지막으로 전체 네트워크에 backward function을 넣어보자.

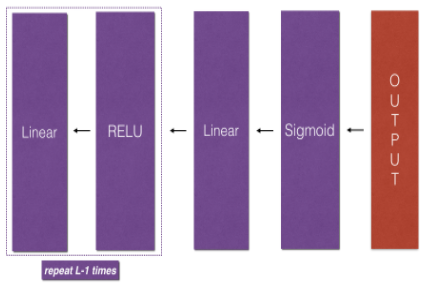
위 사진과 같이 backward가 전달된다.
참고로 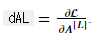을 계산하기 위해서는
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL)) 이 코드를 입력하면 된다.
천천히 빌드해보자.

def L_model_backward(AL, Y, caches):
    grads = {}
    L = len(caches) # the number of layers
    m = AL.shape[1]
    Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
    
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
    
    current_cache = caches[L-1]
    dA_prev_temp, dW_temp, db_temp = linear_activation_backward(dAL, current_cache, activation="sigmoid")
    grads["dA" + str(L-1)] = dA_prev_temp
    grads["dW" + str(L)] = dW_temp
    grads["db" + str(L)] = db_temp
    
    for l in reversed(range(L-1)):
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 1)], current_cache, activation="relu")
        grads["dA" + str(l)] = dA_prev_temp
        grads["dW" + str(l+1)] = dW_temp
        grads["db" + str(l+1)] = db_temp
    
    return grads

forward와 같이 sigmoid는 한번, relu는 L-1번 반복하여 각각의 미분한 값을 구해준다.

Update parameters

위에서 구한 값을 가지고 parameter들을 업데이트 시켜주자.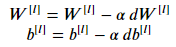
마지막 순서이기도 하고 간단하게 구현할 수 있다.

def update_parameters(params, grads, learning_rate):
    
    parameters = params.copy()
    L = len(parameters) // 2 # number of layers in the neural network
    
    for l in range(L):
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*grads["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*grads["db" + str(l+1)]
    return parameters

여기서 주의해야 할 부분은 learning_rate와 곱하는 값은 backward에서 계산한 gradient여야 하는 것!

이렇게 L-layer의 Neural Network에 대해서 알아봤다.