주택의 가격을 예측한다고 생각해보자.
학습 데이터셋에는 주택 규모(㎡)와 주택 가격이 들어가 있음.
그리고 주택 규모에 따른 가격을 예측하는 모델을 만들고 싶다.
| 주택 규모(㎡) | 주택 가격(백만원) |
|---|---|
| 220 | 325 |
| 135 | 295 |
| 85 | 250 |
| 55 | 176 |
| ... | ... |
✔️ 학습 데이터 각각에 정답(주택 가격)이 주어져 있으므로 지도학습(Supervised Learning)이며,
✔️ 주택 가격을 연속된 값으로 예측하는 것이므로 회귀 문제임
머신러닝 모델을 어떻게 만들까?
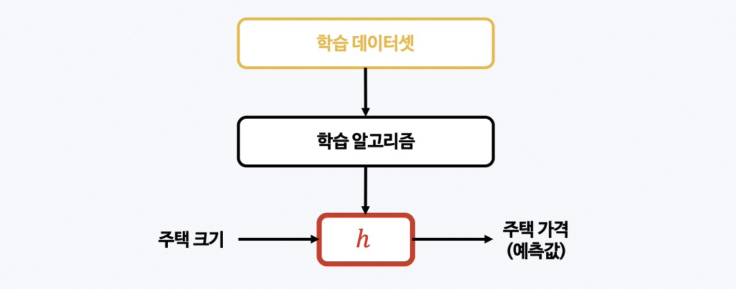
h = hypothesis로, 가설(=모델)을 의미한다.
머신러닝에서는 “모델이 실제 데이터를 얼마나 잘 설명하는가”를 평가할 때 가설 기반의 사고를 쓴다.
예를 들어 선형 회귀라고 했을 때 “가설 함수”는:
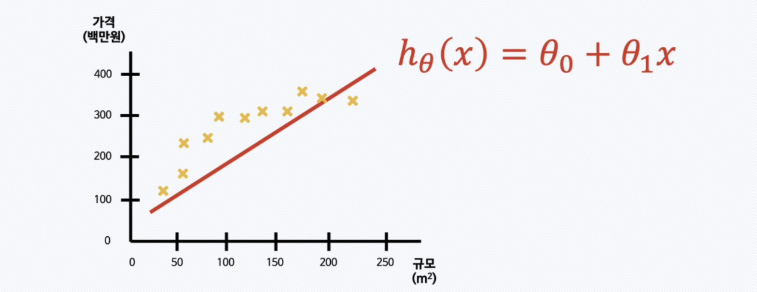
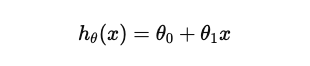
이걸 가설 함수(hypothesis function) 라고 부르고,
데이터를 가장 잘 설명하는 𝜃 값을 찾아가는 게 목표
➡️ 데이터와 가설(모델)의 에러(차이)가 최소가 되게끔 θ₀, θ₁을 설정하면? 가장 좋은 θ₀, θ₁가 된다.
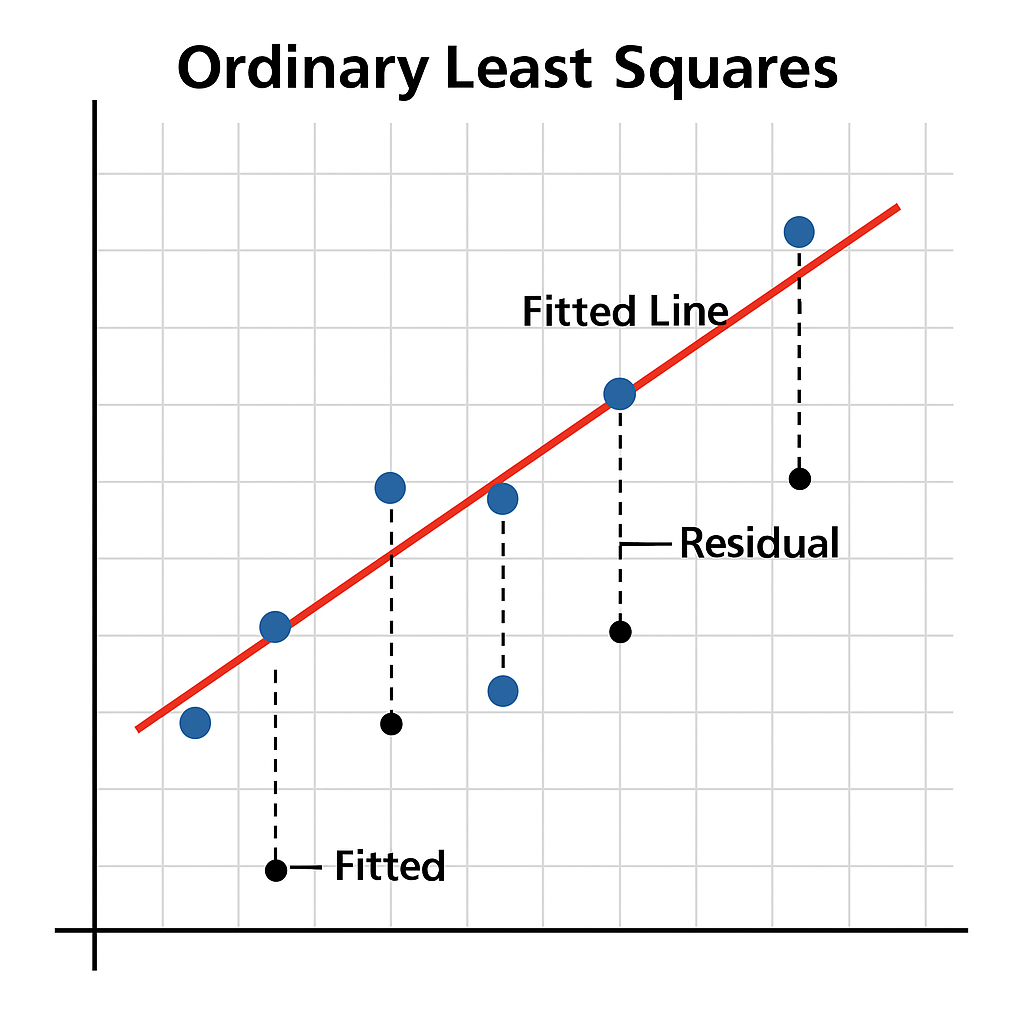
OLS: Ordinary Linear Least Square (최소자승법)
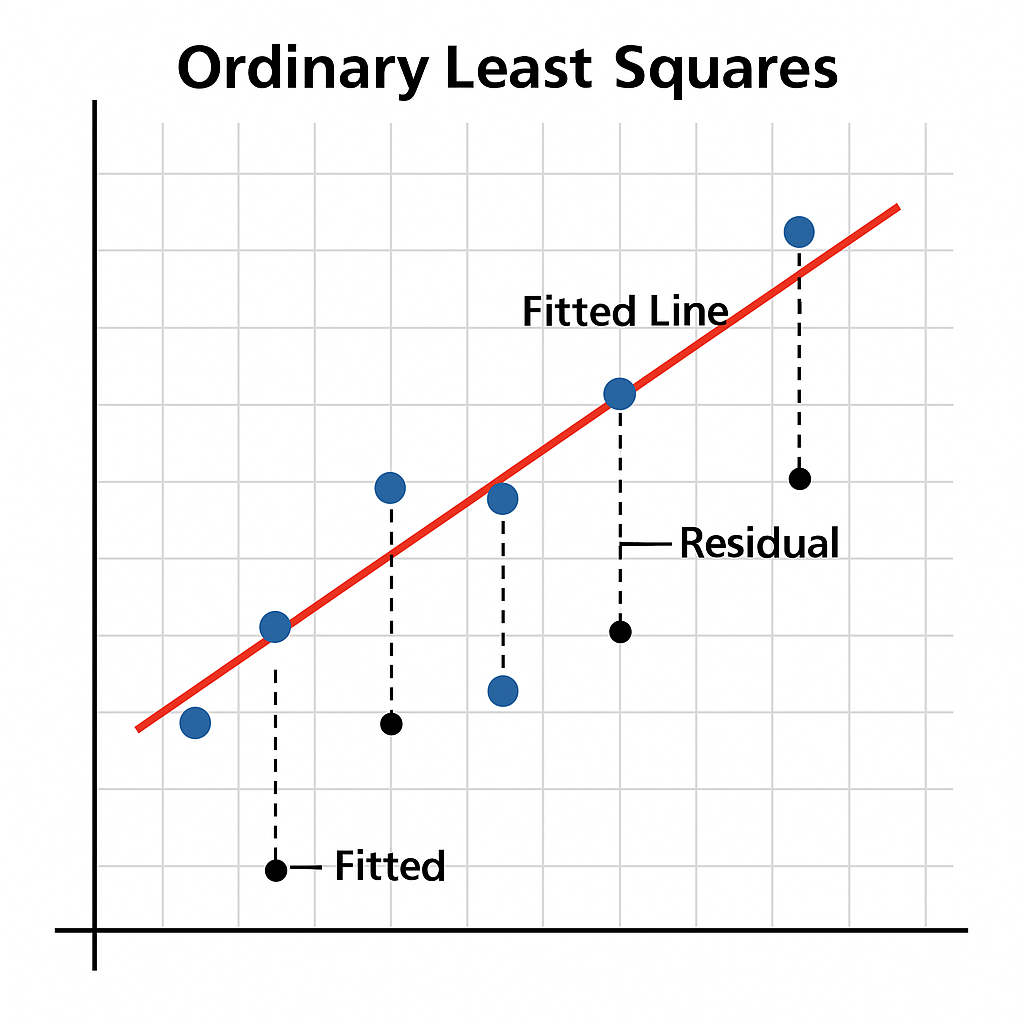
Ordinary Least Squares, 일반 최소제곱법이라고도 함
회귀분석에서 가장 널리 쓰이는 방법 중 하나로, 선형회귀를 하는 가장 간단하고도 오래된 방법이다.
간단히 말하면, 데이터와 예측 값 사이의 거리(오차)를 제곱해서, 그 합이 최소가 되도록 직선을 그리는 방법.
벡터/행렬을 이용한 선형 회귀 공식
(1,2), (2,3), (3,4), (4,6), (5,5)
이 5개의 데이터를 가장 잘 설명하는 하나의 직선을 그린다면 어떻게 그려야 할까?
y = ax + b에 5개의 x, y를 대입해서 행렬 벡터로 만들어서 어쩌구저쩌고 OLS 공식을 통해 최소제곱해를 구해주면 되는데..
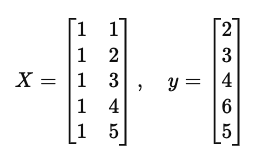
OLS 공식(최소제곱해 구하는 공식)을 통해
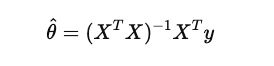
세타 벡터를 구함
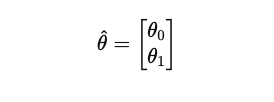
그럼 이런 형태의 직선을 구할 수 있음
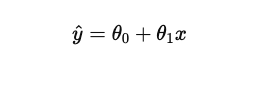
y = 1.1x + 0.5가 나온다고 함
좀 복잡하고 어렵지만 python 코드 한줄이면 수기 계산 대신 이걸 편하게 구할 수 있다..
OLS 예시
데이터를 이렇게 갖고 있다고 가정:
- 𝑥: 주택 크기
- 𝑦: 실제 집값
이때, 가설 함수는
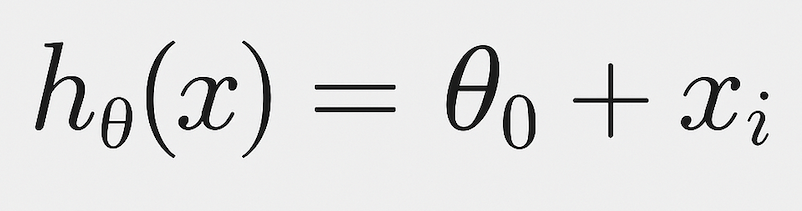
그럼 각 데이터마다 오차는 이렇게 나와:
오차 = 
이걸 제곱해서 다 더하면?
비용 함수 (Cost Function) =
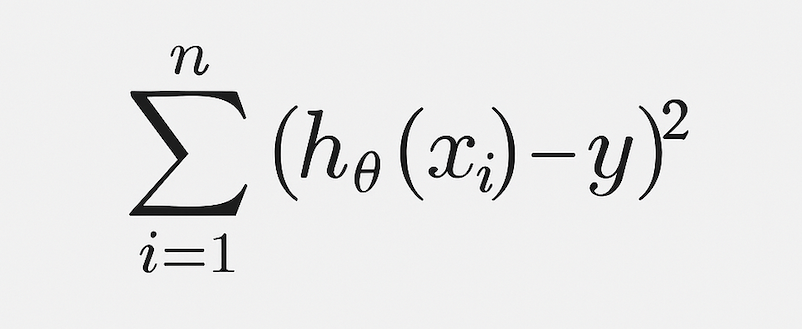
제곱하는 이유:
- 절대값보다 제곱이 수학적으로 다루기 쉬움
- 큰 오차에 벌점을 크게 주는 효과 (Outlier에 민감)
이 비용 함수가 최소가 되도록 θ₀, θ₁을 찾아주는 게 바로 OLS 🙌
OLS의 특징
- 해석이 직관적이고 간단
- 계산도 효율적 (특히 선형 회귀에 딱)
- 다만, 이상치(outlier) 에 민감할 수 있음
파이썬으로 해보자
데이터 만들기
import pandas as pd
data = {'x':[1., 2., 3., 4., 5.], 'y':[1., 3., 4., 6., 5.]}
df = pd.DataFrame(data)
df
scatterplot으로 그리면,
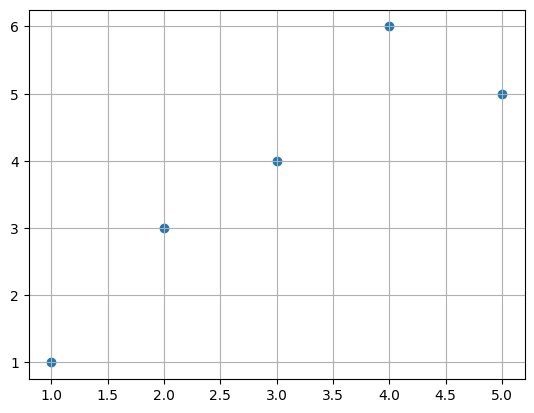
Scikit-Learn이 제공하는 OLS 방법인 LinearRegression 사용해보자
LinearRegression을 만들어준뒤 fit으로 훈련시키기~
from sklearn.linear_model import LinearRegression
X = df[['x']]
y = df['y']
reg = LinearRegression()
reg.fit(X, y) 그러면 나오는 예측값
pred = reg.predict(X)
pred
y값과 pred로 scatter를 그려보면
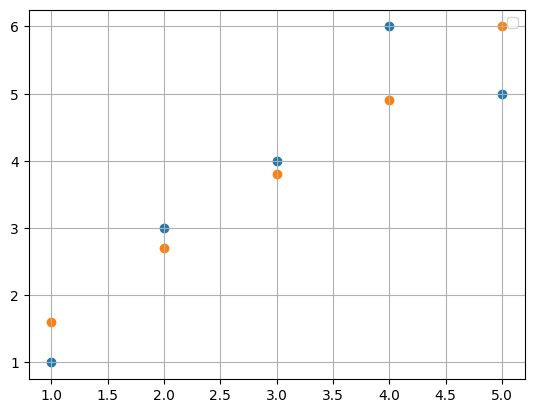
모델의 해석을 위해, 에러 절대값들에 평균을 내보면?
(= mean absolute error, MAE라고 줄여서 말함)
import numpy as np
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y, pred)
0.64가 나온다. 이거말고 MSE, RMSE도 있는데 이건 다음에
직관적으로 그래프를 그려보면~
(x 축에 참 값, y축에 예측값을 넣고, 비교를 위해 x=y 그래프도 그려줌)
plt.scatter(y, pred)
plt.plot([0, 6], [0, 6], 'r')
plt.xlabel('Actual')
plt.ylabel('Predict')
plt.title('Real vs Predict')
plt.grid()
plt.show()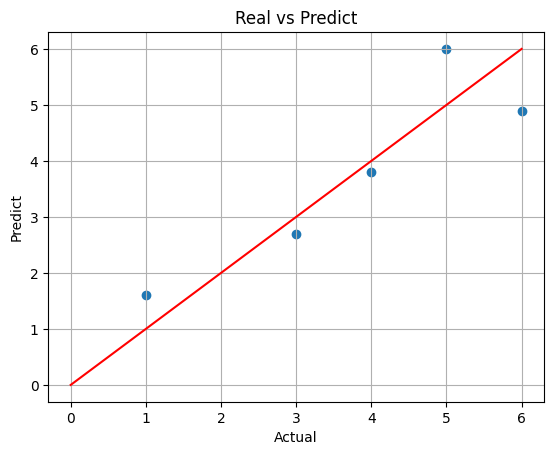
이렇게 눈으로 확인할 수 있다. 👀
(이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.)
