머신러닝의 종류

• 지도학습: 정답을 주고 학습시키는 것
• 비지도학습: 정답이 없음
• 강화학습 (제로베이스 데이터스쿨 과정에서는 다루지 않음)

지도학습의 종류

분류 Classification

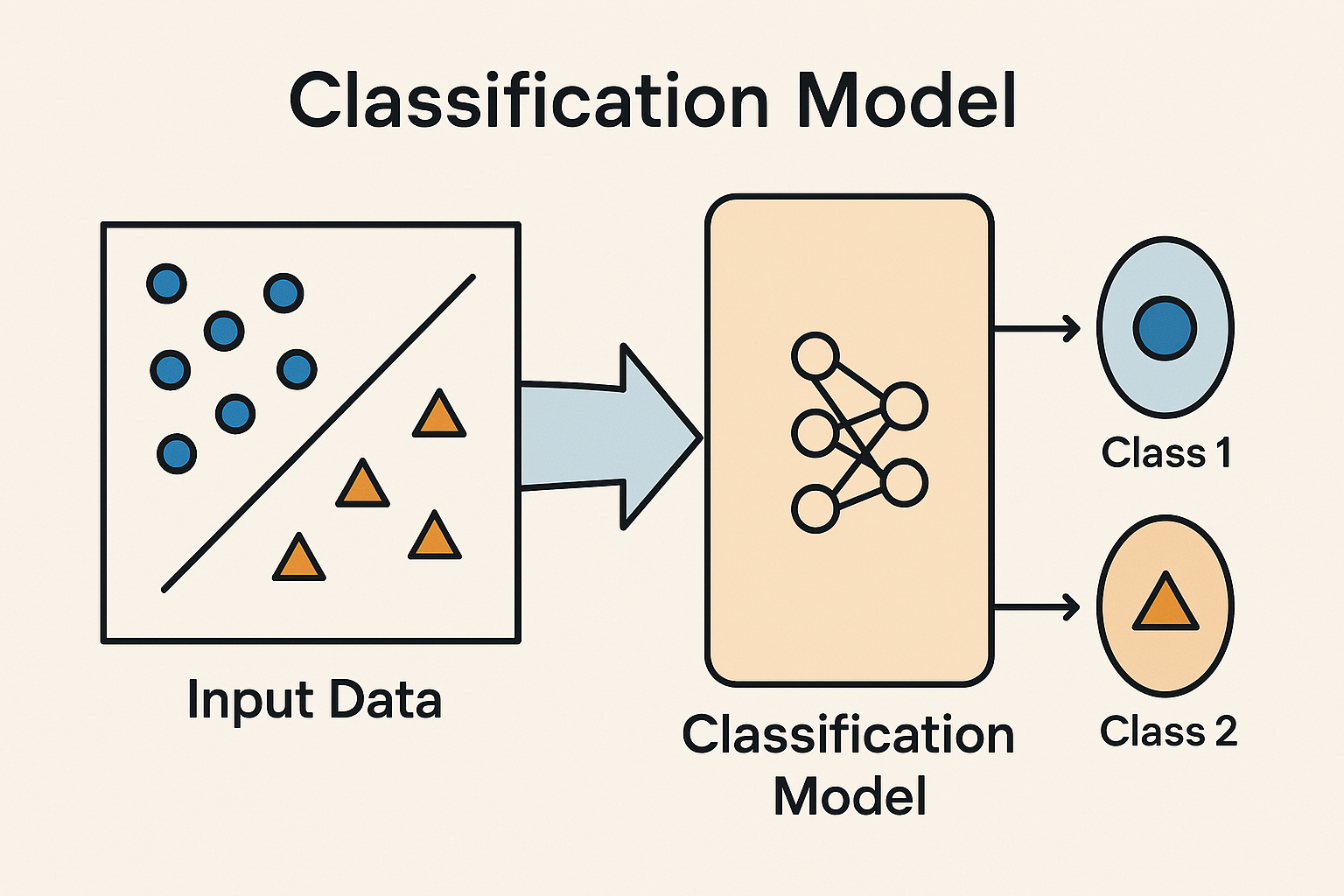
• 데이터를 보고 정해진 카테고리 중 하나로 분류하는 모델
• 새로운 Instance를 주었을 때 어떤 Label을 붙일지 결정하는 모델. 예를 들어:
  • 이메일이 스팸인지 정상인지
  • 사진 속 동물이 강아지, 고양이, 토끼 중 어떤 건지
  • 고객이 이탈할지 안 할지
    ➡️ 뭔가 정답이 정해진 범주(클래스) 중 하나를 고르는 문제에 사용돼.

🧩 작동 방식 (간단히):

1. 데이터를 입력하면
2. 특징(Feature)을 분석해서
3. 어떤 클래스에 속할 확률이 높은지 계산해서
4. 그중 가장 높은 확률의 클래스를 예측함

📊 분류 모델 예시

• 로지스틱 회귀(Logistic Regression) ← 선형 분류 문제에 좋다고 함
• KNN (K-최근접 이웃) ← 주변 데이터 기반
• 결정 트리 / 랜덤 포레스트
• 서포트 벡터 머신(SVM)
• 신경망 (Neural Networks) ← 복잡한 분류 문제에 강함

✨ 주요 특징

• 출력이 연속값이 아니라 클래스(label) 예: [고양이, 강아지, 토끼]
• 정확도(Accuracy), 정밀도(Precision), 재현율(Recall) 같은 지표로 성능 평가

회귀 Regression

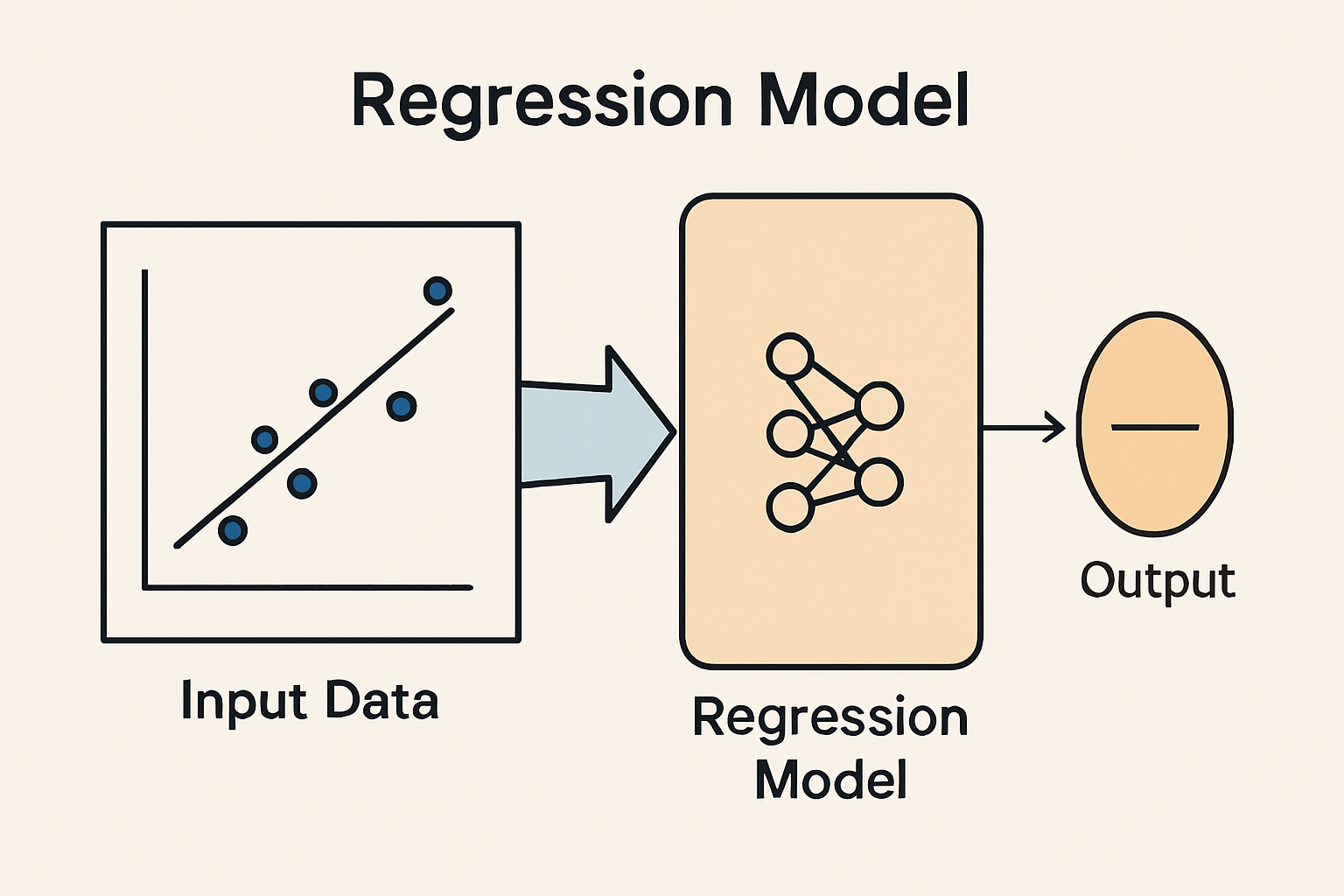
• 연속적인 값을 예측하는 머신러닝 기법
• 회귀의 특징은, 정답이 '연속적'이라는 것. 예를 들어:
  • 집의 면적으로 가격을 예측할 때
  • 날씨의 기온으로 아이스크림 판매량을 예측할 때
  • 키, 몸무게 등 (몸무게가 55.634512...kg)
    ➡️ 이런 문제들은 '분류'처럼 특정 카테고리를 고르는 게 아니라, 숫자 값을 예측하는 거니까 회귀 모델을 써야한다.

🧠 작동 방식 (쉽게 말하면):

1. 입력값(x)을 받고
2. 어떤 패턴(선형이든 비선형이든)을 찾아서
3. 출력값(y, 예측 값)을 내는 구조

예를 들어, 선형 회귀는 이런 수식 형태:

𝑦 = 𝑤𝑥 + 𝑏

w: 기울기 (weight)
b: 절편 (bias)
x: 입력값
y: 예측값

🤖 회귀 모델 종류 예시

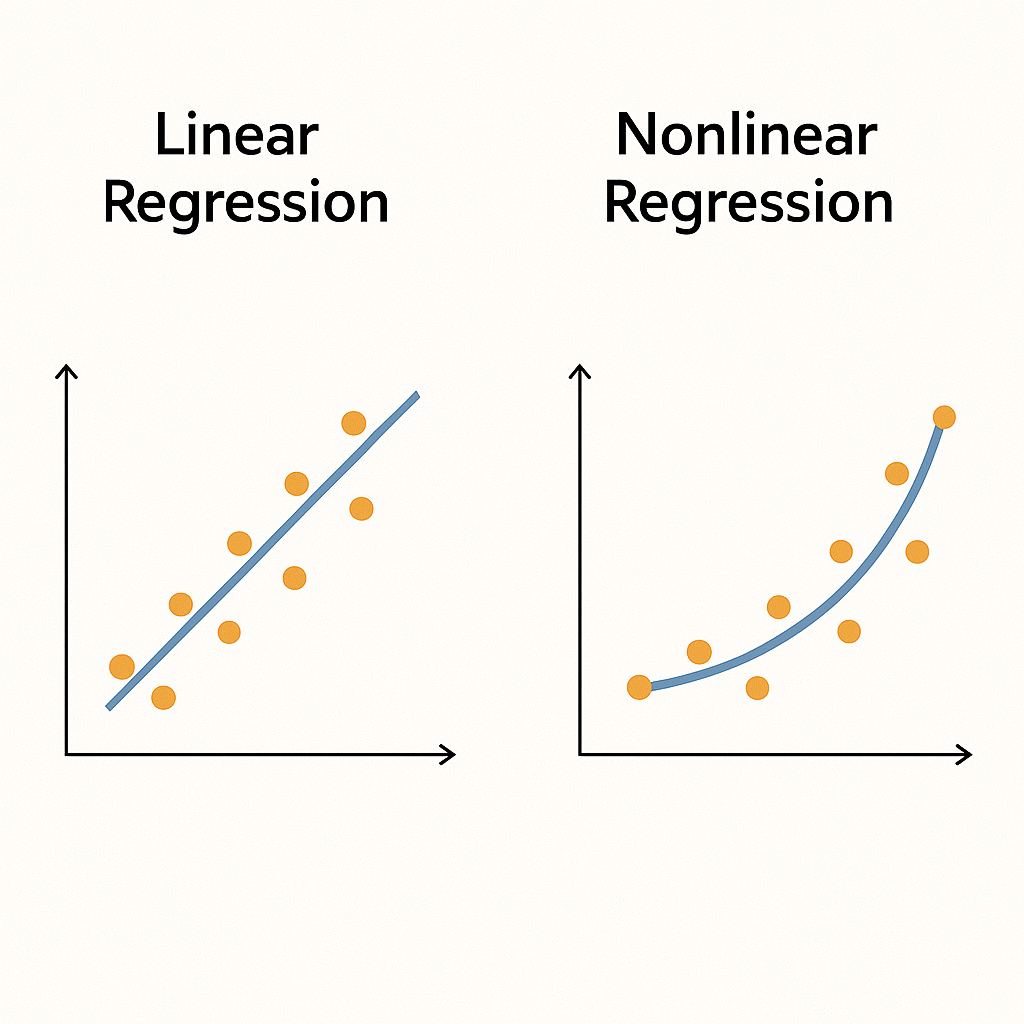
• 선형 회귀 (Linear Regression): 입력과 출력이 직선 관계일 때
• 다항 회귀 (Polynomial Regression): 입력과 출력이 곡선 형태의 관계일 때
• 릿지/라쏘 회귀: 정규화를 포함한 회귀
• 랜덤 포레스트 회귀, XGBoost 회귀 등: 비선형 관계도 잘 다루는 모델들

비지도 학습의 종류

군집

(예시 그림: K-means Clustering)

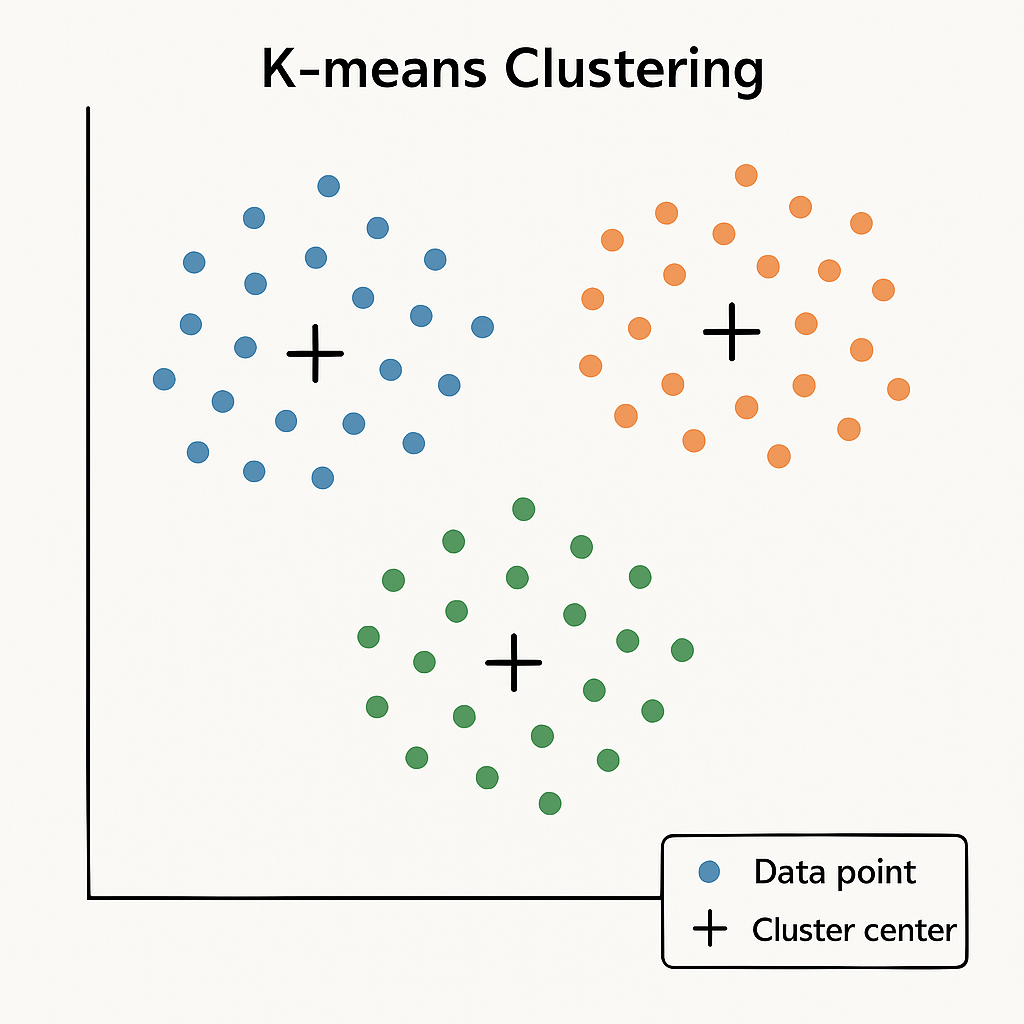
• 데이터를 비슷한 특성끼리 그룹(Cluster)으로 묶는 것
  📌 중요 포인트
  👉 라벨(정답)이 없어서 비지도 학습(unsupervised learning)에 해당함
• 예를 들어:
  • 고객을 소비 패턴에 따라 그룹 나누기
  • 영화 취향이 비슷한 사람들끼리 묶기
  • 웹사이트 방문자 유형 분류
  • 이미지에서 비슷한 색깔끼리 묶기

⚙️ 작동 방식

1. 각 데이터를 벡터 공간에 놓고
2. 서로 간의 거리(유사도)를 기준으로
3. 비슷한 애들끼리 하나의 그룹으로 묶는 구조

📊 군집 알고리즘 예시

• K-평균(K-Means) 👉 대표적인 간단한 군집화 기법
• DBSCAN 👉 밀도 기반으로 군집화 (노이즈도 구분 가능)
• 계층적 군집화(Hierarchical Clustering) 👉 트리 구조로 분할

💡 군집화 결과는 어떻게 활용되나?

• 고객 세그먼트 분석 (마케팅 타겟팅)
• 이상치 탐지 (다른 애들과 너무 다른 애를 찾는 데 유용)
• 데이터 전처리 or 시각화 용도 등 다양함

차원 축소 (Dimensionality Reduction)

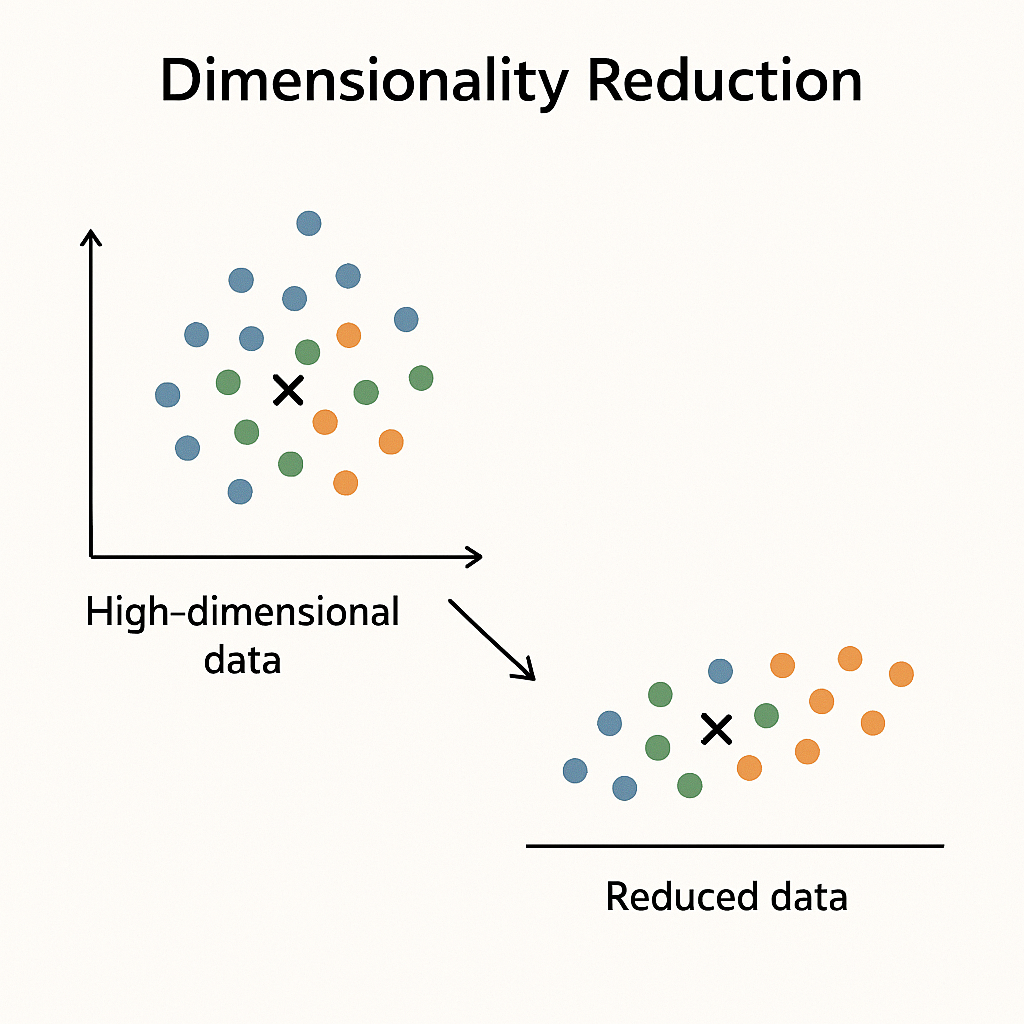
데이터가 너무 많은 특성(Feature) 을 가지고 있으면:

• 시각화가 어렵고,
• 연산 속도도 느려지고,
• 모델 성능도 떨어질 수 있다. 😥

➡️ 그래서,
"중요한 정보는 유지하면서, 덜 중요한 정보는 줄여서 차원을 축소"하는 것

✨ 예를 들어:

• 사진 한 장은 수천 개의 픽셀 → 이걸 2~3차원으로 줄이면 시각화가 가능
• 설문조사 100문항 → 핵심 유형만 뽑아내기

차원 축소 알고리즘

1. PCA (주성분 분석)

   • 가장 대표적인 차원 축소 방법.
   • 데이터를 회전시켜서 가장 분산이 큰 축을 기준으로 재구성함
   • 정보를 가장 잘 보존하는 새로운 축으로 바꿔주는 것

2. t-SNE

   • 복잡한 데이터(예: 이미지, 단어 벡터)를 2D로 예쁘게 시각화할 때 좋음
   • 고차원의 구조를 보존하면서 시각적으로 보기 좋게 펼쳐줌

3. UMAP

   • t-SNE보다 더 빠르고 구조 보존 잘 함 (최근에 인기가 많다고)

📊 활용 분야

• 데이터 시각화에 많이 쓰임 (고차원을 2D/3D로 보여줌)
• 노이즈 제거
• 특성 선택/축소
• 모델 학습 속도 향상