[CV] Convolution

Yeontachi·2025년 8월 7일

Computer Vision Note

목록 보기

17/47

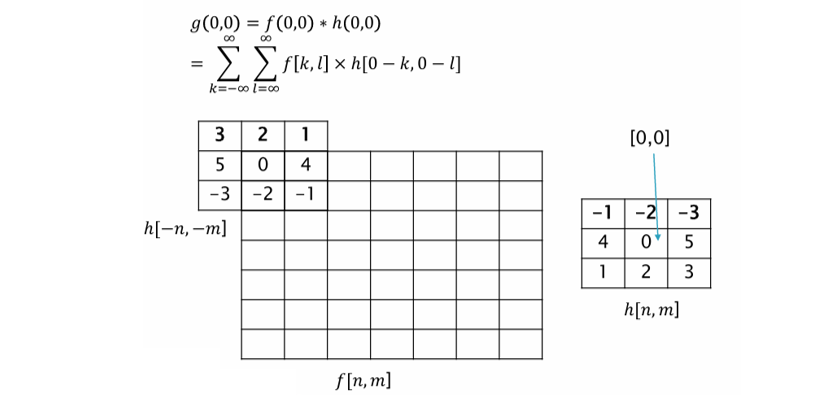
2D 컨볼루션(Convolution)은 이미지 처리에서 입력 이미지 $f$ 와 커널(또는 필터) $h$ 를 결합하여 새로운 출력 이미지 $g$ 를 생성하는 핵심 연산이다. 이 연산은 선형 시불변 시스템(LSI)의 성질을 기반으로 하며, 엣지 검출, 블러, 샤프닝 등 다양한 필터링 작업의 근간이 된다.

컨볼루션은 이미지의 국소적인 이웃 영역(local neighborhood)에서 연산을 수행하며, 커널을 뒤집은 후 이미지 전체를 따라 슬라이딩하며 곱셈과 덧셈을 반복해 결과를 만든다.

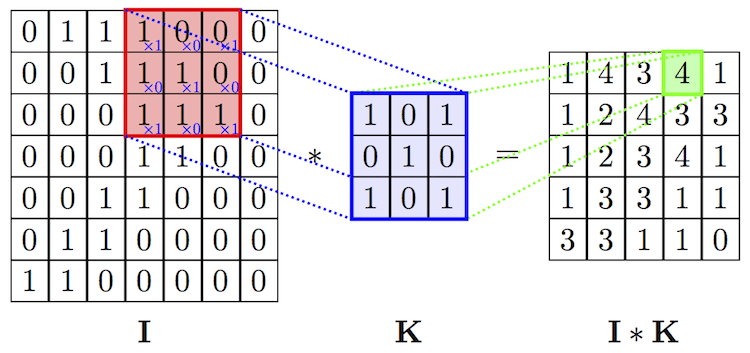
2D Convolution: 수학적 정의

출력 이미지 $g(n,m)$ 는 다음과 같이 계산된다.

g(n, m) = f(n, m) * h(n, m) = \sum_{k=-\infty}^{\infty} \sum_{l=-\infty}^{\infty} f[k, l] \cdot h[n - k, m - l]

$f[k,l]$ : 입력 이미지의 픽셀 값
$h[n-k, m-l]$ : 커널을 상하좌우로 뒤집은 값(CNN에서는 보통 Correlation 사용)
$g[n,m]$ : 위치 (n,m)에서의 출력 픽셀 값

Convolution에 Flip이 포함되는 이유?
컨볼루션은 원래 신호처리(system analysis) 분야에서 사용되던 개념으로 어떤 시스템 $h$ 가 입력 $f$ 에 대해 어떻게 반응하는지를 분석하기 위한 수학적 연산이다.

1D 수식:

(f * h)(t) = \int_{-\infty}^{\infty} f(\tau) \cdot h(t - \tau) \, d\tau

이 식에서의 핵심은 $h(t-\tau) \to$ h를 time-reverse + shift한 것, 즉 시간적으로 뒤집힌 시스템 응답을 입력에 대해 슬라이딩하면서 곱해서 적분하는 방식이다. 이것이 컨볼루션의 정의이며 그 연산을 2D로 확장한 것이 이미지 컨볼루션이다.

Convolution에 대한 정확한 식 정의는 아래 페이지에 정리되어 있다.
Convolution

2D Convolution Example

g(0,0)=f(0,0)*h(0,0) \\= \sum_{=-\infty}^{\infty} \sum_{l=\infty}^{\infty} f[k, l] \times h[0-k, 0-l]

주어진 커널은 아래와 같다고 가정을 하면,

h[n, m] = \begin{bmatrix} -1 & -2 & -3 \\ 4 & 0 & 5 \\ 1 & 2 & 3 \\ \end{bmatrix}

위 이미지에서 좌측의 빈 격자 $f[n,m]$ 는 입력 이미지이며, 우측의 $h[n,m]$ 는 커널(Filter)이다.

$h$ 는 원래 좌표 기준으로 가운데 값(0)이 $[1,1]$ 에 위치하지만, 컨볼루션 정의에 따라 수학적으로 플립(좌우/상하 뒤집힘) 예정이다.

뒤집힌 커널은 아래와 같다.

h[-n, -m] = \begin{bmatrix} 3 & 2 & 1 \\ 5 & 0 & 4 \\ -3 & -2 & -1 \\ \end{bmatrix}

이 커널을 $f[n,m]$ 위에 올려서 곱하고 합산하면 $g(0,0)$ 의 값을 구할 수 있다.

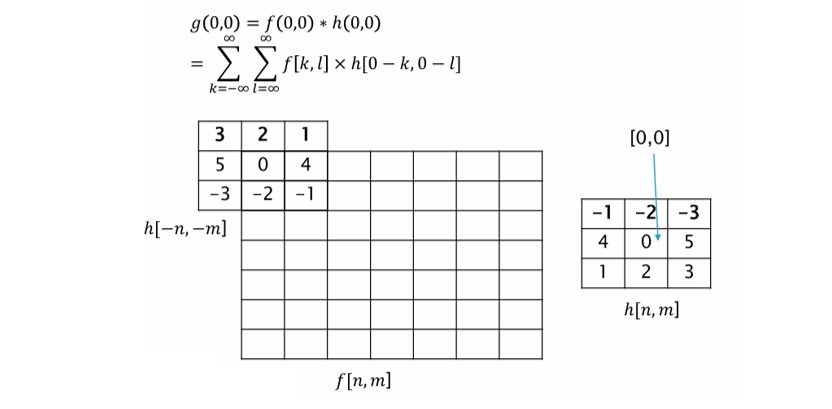
여기서 커널의 중심을 (0,0)에 두는 이유는 필터를 적용할 때, 중심값이 입력 이미지의 현재 픽셀과 정렬되도록 해야한다. 즉, 커널의 중심이 이미지의 현재 위치에 대응되어야 지역적 정보(local context)를 반영한 처리가 가능하다.

예를 들어 커널:

h=\begin{bmatrix}-1&-2&-1\\0&0&0\\1&2&1\end{bmatrix}

이 필터는 수직 에지 검출 필터인데, 가운데 (0,0)에 있는 값이 중심 픽셀과 정렬되어야 수직 방향의 상하 변화량을 올바르게 계산할 수 있다.

아래 이미지는 다양한 커널의 예시이다.

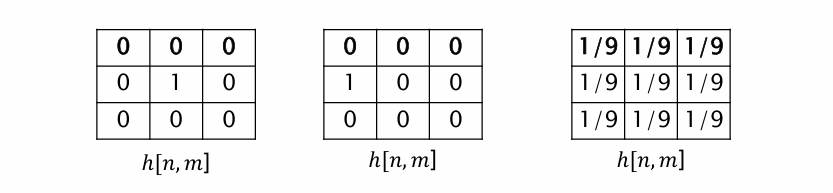
왼쪽 필터는 중앙에만 1이 있고 나머지는 0 $\to$ 입력 이미지의 중앙 값만을 그대로 출력한다.(Identity filter) 중심에 해당하는 픽셀 값만 곱해지고 나머지는 0이 되므로, 결과는 입력 이미지의 원래 픽셀 값이 그대로 유지된다.

가운데 필터는 좌측 중앙이 1이고 나머지는 0이다. 컨볼루션 과정에서 필터가 뒤집히면서 우측 중앙이 1이되고 결과적으로 입력이미지를 좌측으로 한 칸 이동(또는 우측 픽셀 가져오기)한 효과를 보인다.

오른쪽 필터는 모든 값이 $\frac{1}{9}$ 로, 평균 필터이다.(평균값을 계산해서 이미지 부드럽게 만들기 = smoothing)

Kernel Size

커널은 이미지에 적용되는 작은 행렬(보통 3x3, 5x5 등)로 입력 이미지의 주변 픽셀들과 연산을 통해 새로운 픽셀 값을 만들어낸다.

각 커널은 특정한 목적을 가진다. 예를 들면, 흐림, 선명도 향상, 경계 검충 등이 있다.

아래 그림은 다양한 커널 크기의 평균 필터(averaging filter)가 입력 이미지에 적용된 결과를 보여준다.

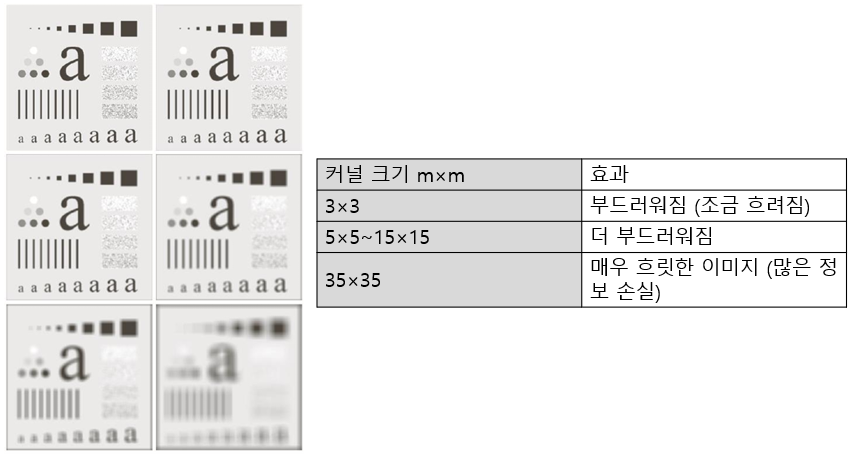
위 이미지에서 볼 수 있듯이 커널이 클수록 더 넓은 영역의 평균을 계산하기 때문에 더 강하게 흐려진다.

원리는 다음과 같다.

g[n,m] = \frac{1}{m^2} \sum_{i=-k}^{k} \sum_{j=-k}^{k} f[n+i, m+j]

여기서 $k = \frac{m-1}{2}$ 이며, 각 픽셀 주변 $m \times m$ 영역의 평균을 계산해 해당 위치에 적용한다.

즉, $m=3$ 일 때, 9개 픽셀의 평균으로 국소적으로만 영향을 미치지만, $m=15$ 일 때, 225개 픽셀의 평균으로 하나의 밝은 점이 주변 어두운 픽셀에 의해 묻힌다. 즉, 출력 $g[n,m]$ 값이 평균적으로 균일해지고, 국소적인 밝은 점이나 경계(contrast)는 약화되며, 그 결과 이미지가 흐릿해(blur) 보인다.(디테일이 평균화되어 사라짐)

아래 이미지는 허블 망원경 이미지에서의 필터링과 이진화를 보여주는 예시이다.

가운데 이미지는 15x15 평균 필터링 결과로, 잡음을 제거하고 밝은 별이나 은하만 부드럽게 남긴다. 이로써 작은 잡음이나 배경 노이즈는 제거된다.

우측 이미지는 Thresholding(임계값 이진화)의 결과로, 평균 필터 후 이미지에 일정 임계값을 줘서, 밝은 부분(별 등)은 흰색(1), 나머지는 검정(0)으로 분리한 결과이다.(객체 검출 전처리)

Sharpening Spatial Filters

Sharpening(샤프닝)은 이미지 내의 윤곽선(edge), 경계(boundary), 세부 구조(detail) 등을 강조하여 더 뚜렷하게 보이도록 하는 공간 도메인 필터링 방법이다.

주요 목적은 밝기(Intensity)의 급격한 변화를 강조하여 흐릿한 이미지를 선명하게 만들기 위함이다.

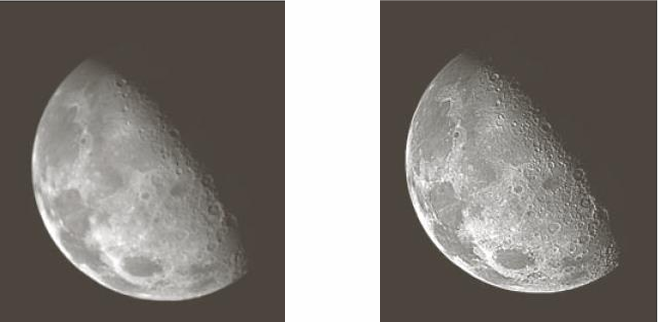
영상에서 경계(edge)는 물체를 구분 짓는 핵심 정보이다. Blur된 이미지는 디테일이 사리지는데 이 디테일을 복원하거나 강조하기 위해 Sharpening이 사용된다.

이미지에서 edge는 밝기(Intensity)의 급격한 변화가 있는 영역을 의미한다.

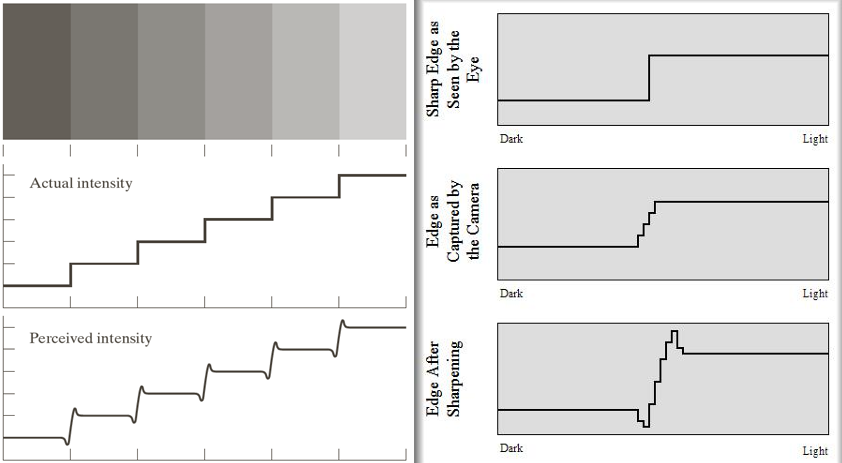
아래 이미지에서, 좌측 그림에서는 실제 밝기는 계단 형태로 증가하지만, Perceived intensity(지각된 강도)는 각 단계마다 overshoot/undershoot가 있는 것처럼 보인다.(Mach Band 효과)

우측 그래프를 보면,

구분	설명
Top: Sharp Edge as seen by eye	우리가 보는 선명한 경계
Middle: Captured by camera	센서에서 계단처럼 뭉개진 형태
Bottom: After sharpening	날카로운 경계를 복원한 결과

각각 다른 결과가 보임을 알수 있다.

1차 및 2차 미분을 통한 경계 검출

1. 1차 미분(First-order Derivative)

\frac{\partial f}{\partial x} = f(x+1) - f(x)

이는 인접한 두 픽셀 간의 밝기 변화량을 측정한다. 경계(edge)가 있는 곳에서는 변화량이 크기 때문에, 이 연산은 Edge Detection에 유용하다.

2. 2차 미분(Second-order Derivative)
1차 미분을 한 번 더 미분하면 2차 미분이다.

\frac{\partial^2 f}{\partial x^2} = \left( f(x+1) - f(x) \right) - \left( f(x) - f(x-1) \right)

이를 정리하면,

\frac{\partial^2 f}{\partial x^2} = f(x+1) + f(x-1) - 2f(x)

이 수식은 중앙값( $f(x)$ )과 그 양 옆 값을 비교하여 곡률(curvature), 즉 형태 변화를 강조한다.

특히 edge나 corner 근처에서 큰 값을 가지므로, Sharpening 필터로 많이 사용된다.

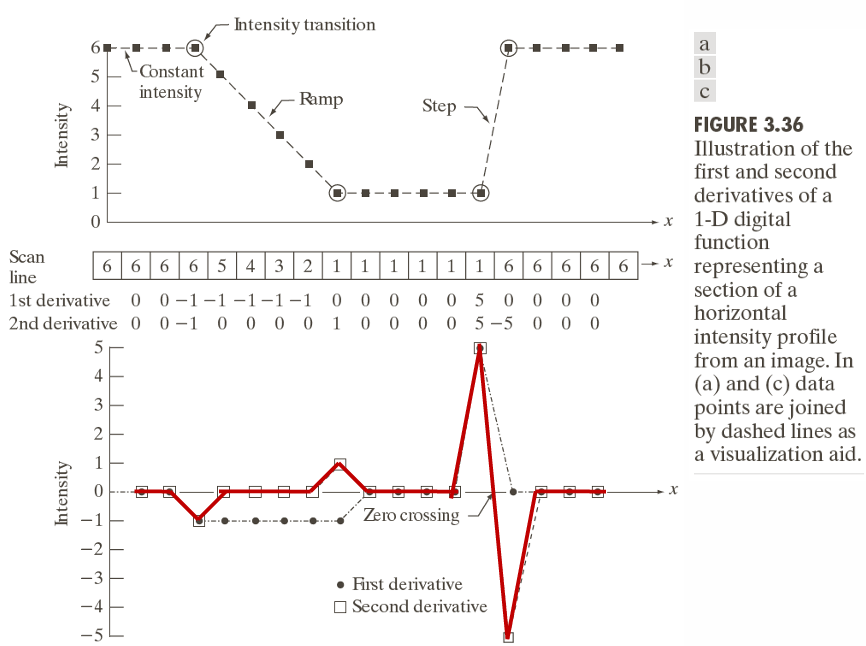
가장 상단의 그래프는 픽셀 밝기(Intensity) 변화를 보여준다. 가로축은 $x$ 방향으로 스캔한 픽셀 위치, 세로축은 해당 위치의 밝기 값이며, 세 영역으로 구분할 수 있다.
1. Constant Intensity : 밝기 변화 없음
2. Ramp : 선형 감소
3. Step : 갑작스러운 밝기 점프(가장 전형적인 Edge)

중간 표는 Scan Line 및 미분 값이다.
Scan Line은 실제 밝기 값의 배열을 의미하며,

1st derivative(1차 미분)은 밝기 차이이며 경계(edge) 근처에서 큰 값 or 급격한 변화가 발생함을 확인할 수 있다.

2nd derivative(2차 미분)은 변화율의 변화로, Zero-crossing이 edge 위치를 나타낸다.

가장 아래 그래프는 미분값을 시각화한 그래프인데, 검은점이 1차 미분 값을 나타내며 edge를 강한 기울기로 표현함을 확인할 수 있다. 빨간 선과 사각형은 2차 미분값을 나타내며, edge에서 양-음 변화(zero-crossing)이 나타나고, 이를 통해 경계의 정확한 위치를 감지할 수 있다.

구분	의미	역할
1차 미분	밝기 변화량 (gradient)	Edge 강도 강조
2차 미분	변화율의 변화	Edge 위치 탐지 (zero crossing)
Zero crossing	2차 미분이 0을 지나가는 지점	가장자리(edge)의 중심 추정 가능

Laplacian Filter

이미지 샤프닝(Sharpening)은 에지(edge) 또는 강한 밝기 변화(transition)를 강조하는 데 사용된다. 이러한 연산은 보통 고주파 성분을 강조하고, 윤곽선을 뚜렷하게 만드는 것이 목적이다.

특히 Laplacian 연산자는 영상의 두 번째 미분(2nd derivative)에 해당하며, 이미지의 경계(에지)가 있는 부분에서 응답하게 된다.

수학적 정의
x,y방향 모두에 2차 미분을 적용하면,

\frac{\partial^2 f}{\partial x^2} = f(x+1) + f(x-1) - 2f(x)

\frac{\partial^2 f}{\partial y^2} = f(y+1) + f(y-1) - 2f(y)

Laplacian 연산자는 다음과 같이 정의된다.

\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}

= f(x+1, y) + f(x-1, y) + f(x, y+1) + f(x, y-1) - 4f(x, y)

이 수식을 필터 마스크 형태로 표현하면 다음과 같다.

Laplacian 필터는 다양한 구현 형태가 존재한다. 사용 목적에 맞게 필터를 골라 사용하면 된다.

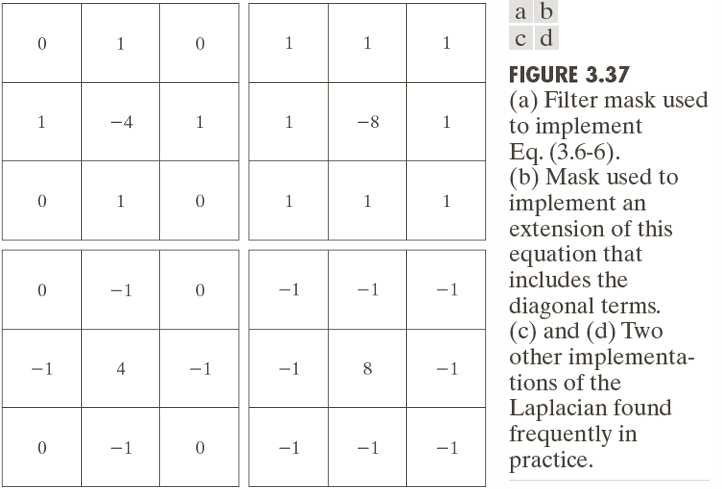
(a)는 기본 4방향 Laplacian 필터이다. 중심 픽셀을 기준으로 상하좌우 방향의 변화만 반영한다. 가장 단순하며, 널리 사용되는 형태이다.

(b)는 대각선까지 포함한 확장 Laplacian 필터이다. 대각선 방향까지 고려하여 더 민감한 에지 검출이 가능하다.

(c)는 중심이 양수인 Laplacian 필터이다. 중심이 양수이고, 주변은 음수이다. 결과 이미지가 중심을 기준으로 밝아질 수 있어 강조 효과가 다르게 나타난다.

(d)는 중심이 양수이고 8방향을 고려한 Laplacian 필터이다. 8방향을 모두 포함하며 중심이 양수이다. 더욱 강력한 에지를 강조할 때 사용된다.

즉, Laplacian은 에지 위치에서 강한 응답을 보인다. 하지만 Laplacian 자체는 에지만 검출하고, 원본 정보는 제거한다. 따라서 일반적으로 원본 영상과 Laplacian 결과를 더해서 샤프닝을 한다.

g(x,y) = f(x,y) - \nabla^2f(x,y)

이때 부호는 마스크 형태에 따라 + 또는 -가 된다.

그림 설명(Fig3.39)

Label	내용	설명
a	Original Signal	원래 신호, 즉 원본 이미지의 1D 단면
b	Blurred Signal	블러된(평균 필터 등으로 부드럽게 한) 신호
c	Unsharp Mask	원본 - 블러된 신호 즉, 엣지만 남은 마스크 (샤프닝 성분)
d	Sharpened Signal	원본 + 언샤프 마스크 → 더 선명한 신호 완성

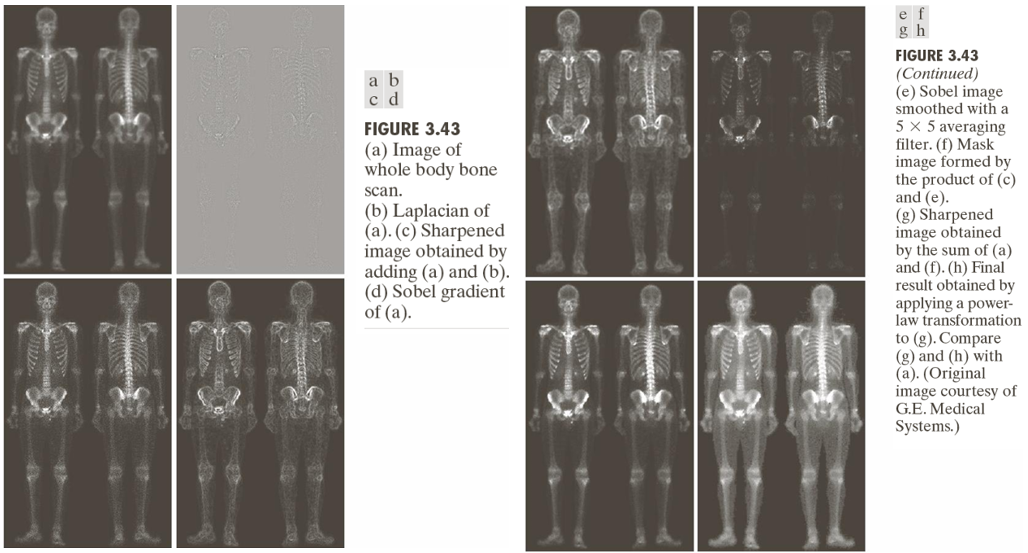
Examples

Boundary in 2D Convolution(경계 처리)

2D Convolution에서는 필터(kernel)가 입력 이미지의 모든 위치를 순회하면서 연산을 수행한다. 이때 출력 이미지의 크기는 아래 식으로 계산된다.

Output\,Size = (N_1, + N_2 -1,M_1 + M_2 -1)

$N_1, M_1$ : 입력 이미지 $f[n,m]$ 의 높이와 너비
$N_2, M_2$ : 커널 $h[n,m]$ 의 높이와 너비
이는 full convolution일 때 계산되는 출력 크기이다.(zero-padding 없이 전체 연산)

경계(Boundary) 문제

커널이 입력 이미지의 가장자리에서 벗어나는 경우가 발생한다.

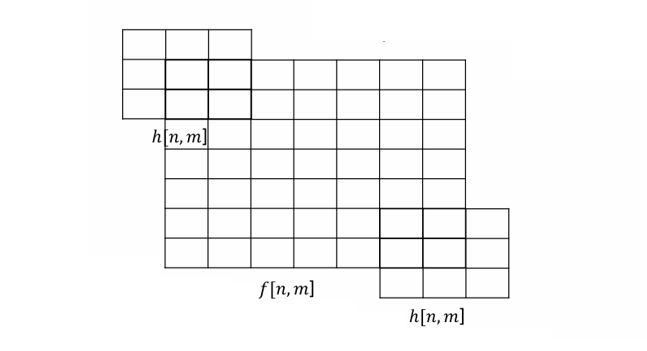
이때 존재하지 않는 픽셀 영역(No Pixel area)을 처리하는 방법이 필요하다.

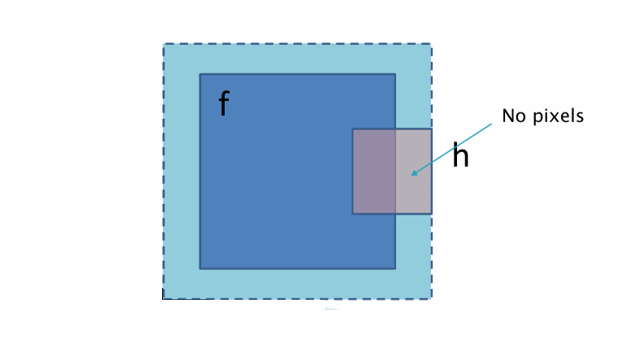
경계 처리 방식

방식	설명
Zero padding	경계 밖은 0으로 간주. ➜ 일반적으로 많이 사용되며, CNN에서 기본 옵션.
Boundary value repetition	경계에 있는 픽셀 값을 그대로 반복하여 채움.
Mirroring (대칭)	이미지 가장자리를 기준으로 대칭적으로 확장.
Wrap around	이미지 반대편 값을 참조. 주기적 구조에서 사용됨.
Crop (valid convolution)	아예 경계를 고려하지 않고 중심 부분만 출력. ➜ 출력 크기는 $(N_1 - N_2 + 1, M_1 - M_2 + 1)$