[CV] Filtering in the Frequency Domain(1) - Frequency Domain

주파수 영역에서의 필터링은 이미지를 구성하는 다양한 주파수 성분(고주파, 저주파 등)에 기반하여 원하는 성분은 통과시키고, 원하지 않는 성분은 제거함으로써 영상을 처리하는 방법이다. 이는 공간 영역 필터링(예: 마스크 연산)과는 다른 접근이며, Fourier Transform을 통해 이미지 데이터를 주파수 영역으로 변환한 후, 해당 도메인에서의 연산을 통해 블러링, 샤프닝, 노이즈 제거 등을 수행할 수 있다.

Backgraound Knowledge: Fourier Transform
Fourier Transform에 대한 이론과 예시는
CV | Fundamentals of Signal Processing(2) - Fourier Transform에서 더 자세히 확인할 수 있다.

Frequency Domain

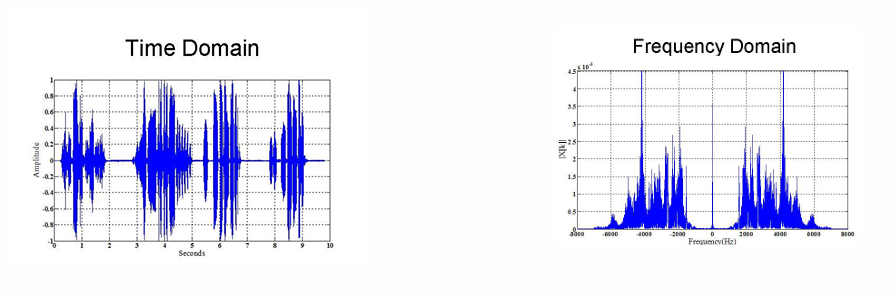
• 시간 영역(Time Domain)
  왼쪽 그래프는 시간(time)에 따라 신호의 진폭(amplitude)이 어떻게 변하는지를 보여준다.(예: 음성, 음악, 센서 데이터 등) 시간 영역에서는 언제 소리가 크고 작았는지 알 수 있지만, 어떤 주파수 성분(저음/고음 등)이 포함되었는지는 알 수 없다.

  $$

• 주파수 영역(Frequency Domain)
  오른쪽 그래프는 푸리에 변환을 통해 얻은 주파수 성분들의 세기(진폭)를 나타낸다. 수평축은 주파수(Hz), 수직축은 각 주파수 성분의 세기(예: |$F(u)$|)
  각 주파수가 얼마나 포함되었는지, 그리고 어떤 성분이 지배적인지를 확인할 수 있다.(그리프의 뾰족한 peak 부분이 해당 주파수가 지배적인 주파수 성분이라는 의미이다.)

• 주파수 영역(Frequency Domain)에서의 성분
  아래는 각 주파수의 파형이 어떤 위치에 해당하는지를 보여주며, 이를 통해 푸리에 변환 결과가 갖는 주요 속성(Property)들을 이해할 수 있다.
  
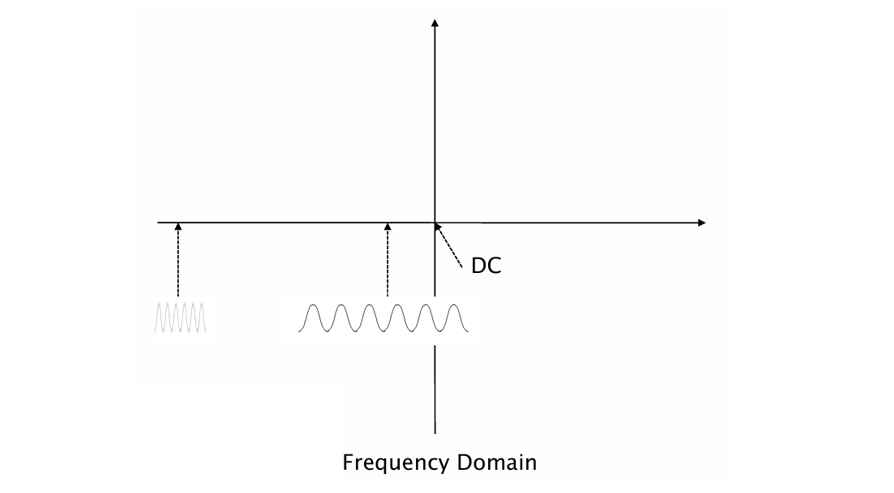
  1. 중앙(원점, DC)
  DC(Direct Current) 성분은 주파수 0에 해당하며, 이는 신호의 평균값 또는 직류 성분(변화 없는 일정한 값)을 의미한다. 이미지에서 중앙의 수직선이 바로 이 DC 성분을 나타내며, 높을수록 전체적인 밝기 값이 크다.(영상의 평균 밝기와 관련)

  2. 중간 주파수 성분
  DC에서 멀어질수록 주파수가 높아진다. 그림 중간의 파형은 중간 주파수 성분을 의미하며, 이는 느리게 진동하는 형태의 패턴을 나타낸다. 영상에서는 **부드러운 경계나 패턴(예: 그림자, 흐림 등)과 관련이 있다.

  3. 고주파 성분
  좌측 또는 우측 끝에 가까운 파형으로 고주파 성분이다. 빠르게 진동하는 신호로, 영상에서는 에지(edge), 텍스처, 노이즈 등 세밀한 정보와 관련되어 있다. 고주파 성분이 많으면 영상이 샤프(선명)해지며, 고주파를 제거하면 블러(흐림)효과가 나타난다.

Fourier Spectrum Examples

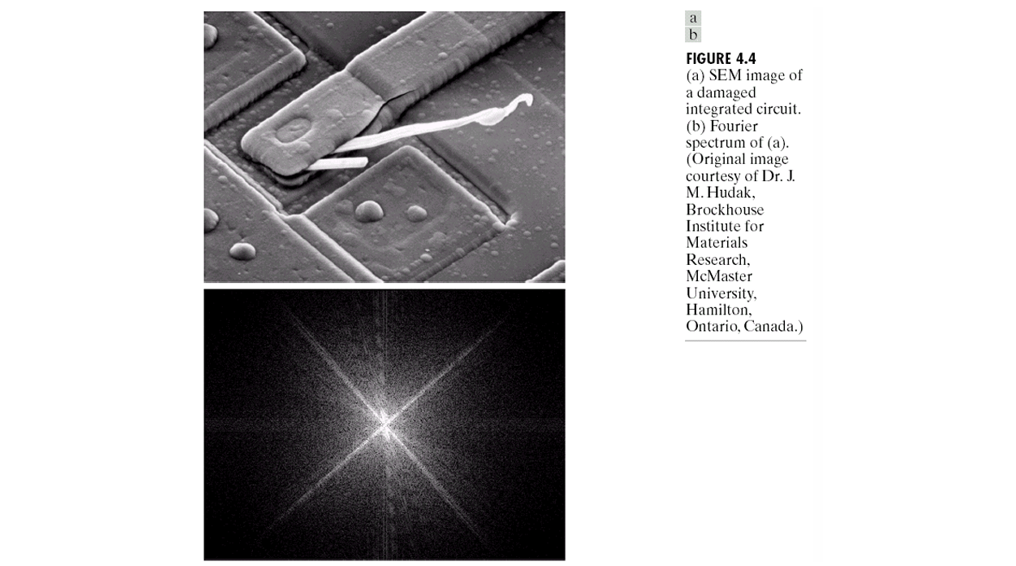
위 원본 이미지는 SEM(주사 전자 현미경)으로 촬영된 손상된 집적 회로의 고해상도 이미지이다. 아래 이미지는 위 원본 이미지에 2D 푸리에 변환을 적용하여 얻은 주파수 스펙트럼(Fourier Spectrum)이다.

여기서 중심은 DC 성분, 즉 평균 밝기이고, 그 주변 밝은 부분은 저주파 구조들이다.

대각선 방향 패턴은 이미지 내의 대각선 방향 구조물 또는 손상된 선이 주파수 도메인에 영향을 주었음을 보여준다.

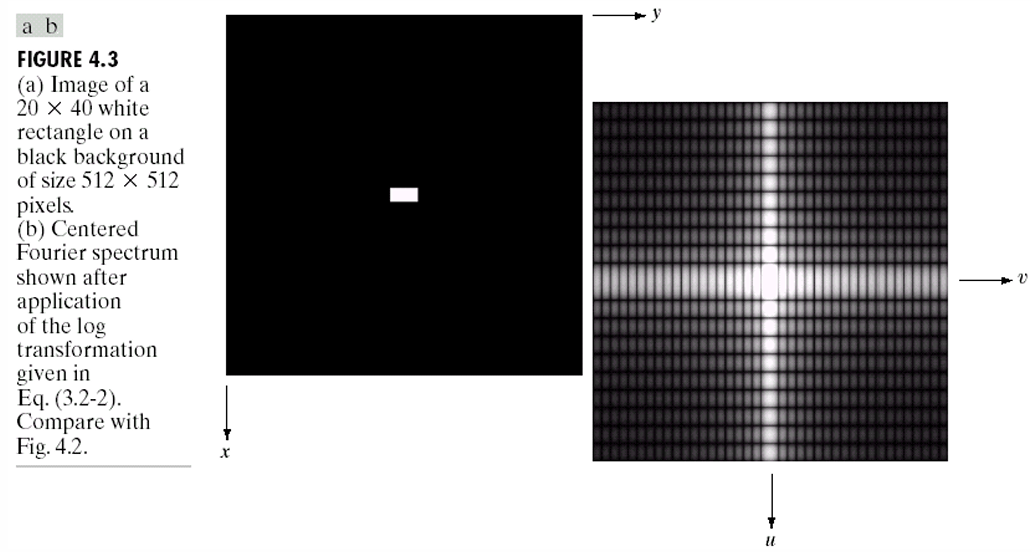
왼쪽 이미지는 가로40, 세로20의 흰 사각형이 위치한 단순 이미지이며, 우측 이미지는 왼쪽 이미지에 대해 2D DFT를 수행한 후 로그 변환(log scaling)을 적용해 스펙트럼을 시각화한 결과이다.

중심의 밝은 점은 DC 성분이며, 이는 사각형의 전체 평균 밝기를 의미한다. 수평 및 수직 방향으로 밝은 주기적 줄무늬가 펴져 있으며, 이는 사각형의 수직, 수평 가장자리(edge)가 강한 주파수 성분을 만들었음을 의미한다.

원본 이미지의 사각형의 경계는 급격한 밝기 변화(=고주파 성분)을 발생시키기 때문에 스펙프럼의 고주파 성분 또한 확인할 수 있다.

2D DFT(Discrete Fourier Transform)

• $f(x, y)$: 입력 영상 (공간 도메인)
• $F(u, v)$: 주파수 성분을 나타내는 스펙트럼 (주파수 도메인)
• $M \times N$: 이미지의 가로 × 세로 해상도
• $u, v$: 수직/수평 방향 주파수 인덱스

영상은 2차원 신호이므로, 1D DFT를 x방향, y방향으로 두 번 연속 적용하면 2D DFT가 된다.

실제 구현에서도 2D DFT는 보통 두 번의 1D DFT로 처리된다. 즉, $f(x,y)를 먼저 행(row) 기준으로 DFT, 그 다음 열(column) 기준으로 DFT 수행한다.

2D IDFT(Inverse DFT)

• $F(u, v)$: 주파수 도메인에서의 데이터
• $f(x, y)$: 복원된 공간 도메인 이미지

역 변환에는 $\frac{1}{MN}$이 빠진 대신, 정방향 DFT에 정규화 $\frac{1}{MN}$이 포함되어 있으므로 상쇄된다.(단방향 정규화 방식)

2차원 DFT는 이미지를 주파수 영역으로 변환함으로써, 단순히 픽셀 값의 배열로는 알기 어려운 이미지의 주파수적 특성을 분석할 수 있게 해준다. 이러한 변환을 통해 우리는 이미지가 어떤 주파수 성분으로 구성되어 있는지를 파악할 수 있으며, 이 주파수 성분은 다양한 영상 처리 작업에서 핵심적인 역할을 한다.

예를 들어, 이미지의 저주파 성분은 주로 배경이나 부드러운 영역에 해당하며, 이미지 전체의 윤곽이나 밝기 변화 같은 큰 구조를 표현한다. 반면 고주파 성분은 경계(edge), 세부 텍스처, 노이즈 등과 같이 급격한 변화가 있는 부분에 해당한다. 즉, 주파수 성분을 분석함으로써 이미지의 구조적 특징을 효과적으로 분리해낼 수 있다.

이러한 주파수 정보는 실질적인 응용에서도 유용하게 활용된다. 주파수 도메인에서 특정 범위의 성분만 선택적으로 통과시키거나 제거하는 방식으로, 샤프닝(Sharpening), 블러링(Blurring), 노이즈 제거와 같은 다양한 필터링 작업을 수행할 수 있다. 예를 들어, 고주파를 제거하면 부드러운 이미지를 만들 수 있고, 반대로 고주파를 강조하면 경계가 또렷한 이미지를 만들 수 있다.

또한 주파수 기반 표현은 이미지 압축에서도 핵심적인 역할을 한다. 실제로 JPEG와 같은 압축 알고리즘은 이미지에서 중요한 주파수 성분만 남기고, 덜 중요한 고주파 성분은 제거함으로써 데이터 양을 줄인다. 이렇게 하면 눈에 띄는 정보는 유지하면서도 저장 공간을 효과적으로 줄일 수 있다.

References

References
Images from Rafael C. Gonzalez and Richard E.
Wood, Digital Image Processing, 2nd Edition.