[CV] Filtering in the Frequency Domain(2) - Image Smoothing Using Lowpass Filters

Yeontachi·2025년 8월 8일

Computer Vision Note

목록 보기

19/47

주파수 영역 필터링은 이미지를 푸리에 변환 후, 원하는 주파수 성분만 통과시키고 나머지는 제거하거나 약화시키는 방식으로 처리하는 기법이다. 이는 공간 도메인에서의 컨볼루션(convolution) 연산과 동일한 역할을 하지만, 계산적으로 더 효율적인 경우가 많다.

아래 수식은 공간 도메인(Spatial Domain)에서의 2D 선형 필터링(컨볼루션)이다.

g(x,y) = \sum_{i=-a}^a\sum_{j=-b}^bh(i,j) \cdot f(x-i, y-j)

$f(x, y)$ : 입력 이미지
$h(i,j)$ : 필터 마스크(kernel)
$g(x,y)$ : 필터링된 출력 이미지
이 식은 필터 $h$ 를 이미지 $f$ 에 슬라이딩하며 곱하고 더하는 컨볼루션 연산을 의미한다.

하지만 이와 동일한 작업을 주파수 도메인에서는 다음과 같은 방식으로 수행한다.

G(x,y) = H(u,v) \cdot F(u,v)

즉, 컨볼루션 연산은 주파수 도메인(Frequency Domain)에서의 곱셈으로 대체될 수 있으며, 이는 푸리에 변환의 중요한 성질 중 하나이다. 최종적으로 역 푸리에 변환을 통해 다시 이미지 도메인으로 돌아온다.

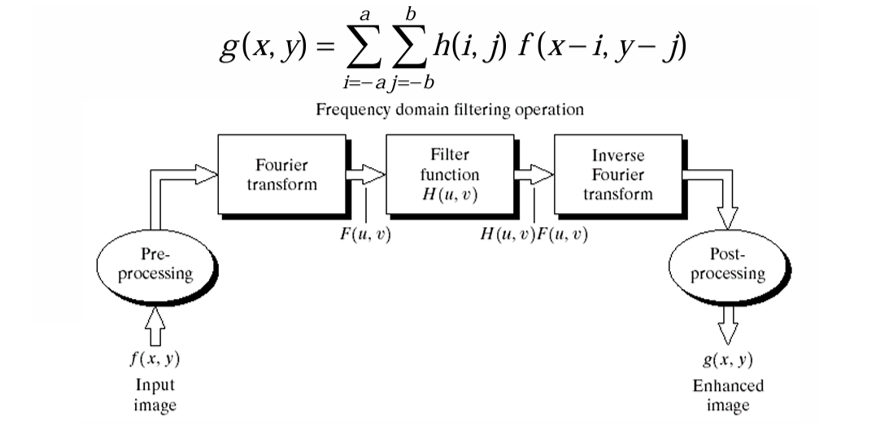
주파수 도메인 필터링을 사용하는 이유?
1. 효율성 : 큰 커널일수록 공간 도메인보다 주파수 도메이니에서 곱셈이 더 빠르다.

2. 선택적 제어 : 특정 주파수 대역(예: 고주파, 저주파)만 정밀하게 조작이 가능하다.

3. 복잡한 필터 설계 : 공간 도메인에서는 구현이 어려운 고급 필터를 주파수 기반으로 쉽게 표현이 가능하다.

4. 노이즈 제거, 샤프닝 : 고주파 제거로 부드럽게 만들거나, 강조하여 샤프라게 만들 수 있다.

Image Smoothing Using Frequency Domain Filiters

스무딩(Smoothing) 또는 블러링(Blurring)은 이미지에서 고주파 성분(고속 변화 = 에지, 노이즈 등)을 제거하여 더 부드럽고 흐릿한 이미지를 만드는 과정이다.

이러한 스무딩은 공간 도메인에서는 평균 필터나 가우시안 필터를 사용하는 반면, 주파수 도메인에서는 고주파 성분을 제거(drop out)하는 방식으로 수행된다.

즉, 고주파 성분을 차단하거나 약화시키는 Low-Pass Filter(저역 통과 필터)를 주파수 영역에서 곱함으로써, 스무딩 효과를 얻는다.

수식
주파수 영역에서의 스무딩은 아래 수식으로 표현된다.

G(u,v) = H(u,v) \cdot F(u,v)

여기서 각 항목의 의미는 다음과 같다.

$F(u,v)$ : 입력 이미지 $f(x,y)$ 의 2D 푸리에 변환
$H(u,v)$ : 필터 전이 함수(Filter Transfer Function) , 일반적으로 저역 통과 필터(Low-Pass Filter)를 사용
$G(u,v)$ : 필터링된 푸리에 스펙트럼 $\to$ 다시 역변환하여 출력 이미지 $g(x,y)$ 를 생성

최종 출력 이미지는 다음과 같다.

g(x,y) = \mathcal{F}^{-1}[G(u,v)] = \mathcal{F}^{-1}[H(u,v) \cdot F(u,v)]

Lowpass Filters

Ideal Lowpass Filters

ideal Lowpass Filter는주파수 영역에서 특정 반지름 $D_0$ 이내의 모든 저주파 성분은 그대로 통과시키고, 그 바깥의 고주파 성분은 완전히 제거하는** 매우 이상적인 필터이다.

이미지에서 고주파는 경계(edge), 텍스처, 노이즈에 해당하고, 저주파는 부드러운 배경이나 천천히 변화하는 밝기 정보에 해당한다.

따라서 Ideal Lowpass Filter를 적용하면 이미지가 부드럽게 흐려지며, 고주파 정보(에지, 잡음 등)는 제거된다.

필터 함수 정의

H(u,v) = \begin{cases}1, \,\,\, \text{if}\,\, D(u,v) ≤ D_0\\0, \,\,\, \text{if}\,\,D(u,v) > D_0 \end{cases}

이는 특정 거리 $D_0$ 이내의 주파수 성분만 통과시키는 원형 필터 형태이다.

거리 함수 $D(u,v)$

D(u,v) = \sqrt{(u-P/2)^2 + (v-Q/2)^2}

$(u,v)$ : 주파수 도메인 상의 좌표
$(P/2, Q/2)$ : 주파수 영역의 중심(DC 성분 위치)
$D(u,v)$ : 현재 좌표에서 중심까지의 거리
$D_0$ : 필터의 컷오프 주파수(이 거리까지만 통과)

아래는 필터 함수 $H(u,v)$ 를 시각적으로 표현한 것이다.

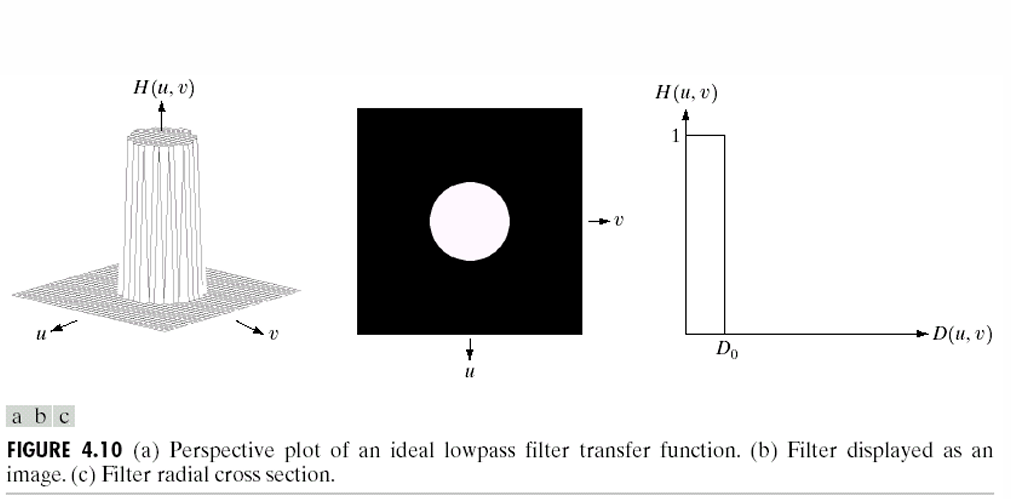
왼쪽 3D 그래프를 보면, 중심을 기준으로 반지름 $D_0$ 이내는 값이 1, 그 외는 0인 원기둥 모양의 형태이다. 즉, 주파수 공간에서 저주파(중앙)만 통과시키고, 고주파(바깥쪽)은 차단함을 시각적으로 보여준다.

가운데 원형 이미지는 실제 필터를 2D 이미지로 표현한 것이다. 흰색 원 부분은 값이 1로 통과, 검정 부분은 값이 0으로 차단이다. 푸리에 스펙트럼과 곰할 때, 이 영역만 남기고 나머지를 날려버리는 마스크 역할을 한다.

우측 단면도는 중심으로부터 거리 $D(u,v)$ 에 따라 필터 값이 어떻게 변하는지 보여주는 횡단면 그래프이다. $D_0$ 까지는 1, 이후는 갑자기 0으로 떨어지는 이상적인 계단 함수 형태이다.

Examples

우측 그림의 동심원은 각각 특정 반지름을 기준으로 주파수 성분을 포함하는 영역을 나타낸다. 그림이 설명하는 바로는 반지름 5,15,30,80,230은 각각 92.0, 94.6, 96.4, 98.0, 99.5%의 에너지 비율을 나타낸다. 즉, 중심에 가까울수록 저주파, 바깥쪽은 고주파 성분을 의미한다.

위 그림은 Ideal Lowpass Filter를 적용한 결과이다. 각 필터는 특정 반지름 내의 저주파만 통과시키고 고주파를 제거하였다. 반지름 값이 작을수록 이미지가 많이 흐려짐을 확인할 수 있다.(Blurring 심함) 반면, 반지름이 클수록 원본에 가깝다.

Butterworth Lowpass Filters

Butterworth 필터는 고주파 성분을 부드럽게 줄여나가는 필터로, 이미지의 고주파 성분(즉, 노이즈나 엣지 등)을 점진적으로 억제하면서 자연스럽게 흐림(blurring)을 유도한다.

수식은 다음과 같다.

H(u,v) = \frac{1}{1+(D(u,v)/D_0)^{2n}}

$D(u,v)$ : 주파수 평면 상의 원점에서 (u,v)까지의 거리
$D_0$ : 컷오프 주파수(cutoff frequency), 필터가 절반의 세기로 통과시키는 경계 주파수
$n$ : 필터의 차수(order) , 값이 클수록 경계가 더 뚜렷해짐

아래는 Butterworth Lowpass Filters를 시각적으로 나타낸 자료이다.

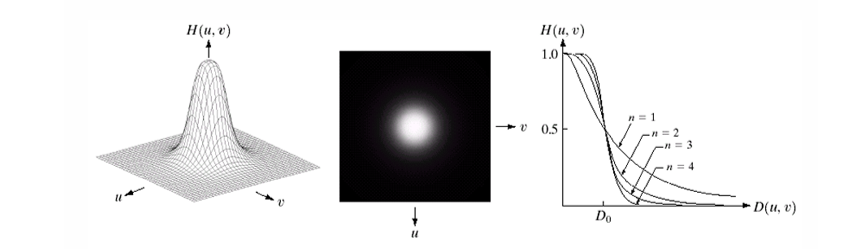
가장 왼쪽은 3D 플롯 형태로, 중심에서 높고, 주변으로 갈수록 완만하게 낮아지는 종형 형태이다. 중심(DC 성분)은 저주파로 통과, 외곽으로 갈수록 고주파들은 점진적으로 억제된다.

가운데 이미지는 필터를 2d 이미지로 표현한 것이다. 중앙 흰색은 통과, 외곽은 점점 어두워짐을 확인할 수 있다. 즉 부드러운 경계가 있는 저주파 통과필터임을 확인할 수 있다.

우측 이미지는 단면 그래프로 여러 차수 $n=1,2,3,4$ 에 따른 $H(u,v)$ 함수의 감소 속도 비교 그래프이다. $n$ 이 커질수록 감소가 가파르고 Ideal Lowpass Filters에 가까워진다.(Ideal Lowpass Filters보다 Ringing 현상이 크기 않음)

좌측은 Ideal Lowpass Filters, 우측은 Butterworth Lowpass Filters를 동일한 조건에서 적용했을 때 이미지 차이를 보여준다. Ideal 필터는 이론적으로 명확하지마나 Ringing 현상이 큼을 확인할 수 있다. Butterworth 필터는 현실적 적용에 더 적합하며, 자연스러운 흐림 효과를 제공한다. 실제 이미지 처리에서는 Butterworth 필터가 더 안정적이다.

Gaussian Lowpass Filter

가우시안 저역통과 필터(Gaussian Lowpass Filter)는 주파수 영역에서 고주파 성분을 부드럽게 제거하여 이미지를 자연스럽게 블러링(흐림)하는데 사용되는 필터이다. 필터의 전달함수는 가우시안 함수 형태를 가지며, 주파수가 중심에서 멀이질수록 지수적으로 감쇠한다.

이 필터는 급격한 변화가 없는 매끄러운 감쇠 곡선을 제공하기 때문에, Ringing 현상이 거의 발생하지 않으며, 시각적으로 가장 부드럽고 자연스러운 결과를 얻을 수 있다.

수식으로 표현하면 아래와 같다.

H(u,v) = e^{-\frac{D^2(u,v)}{2D_0^2}}

$D(u,v)$ : 주파수 도메인에서의 거리
$D_0$ : 컷오프 주파수, 작을수록 더 많은 고주파 성분을 제거한다.
이 함수는 절단 없이 부드럽게 고주파를 감소시킨다.(가우시안 곡선 형태)

아래는 가우시안 필터를 시각화한 자료이다.

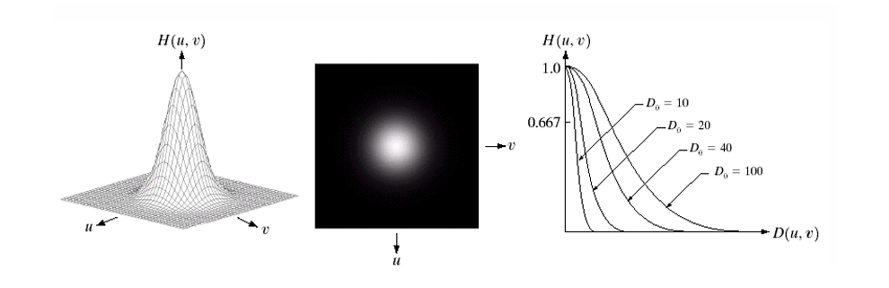
우측 3D로 표현한 가우시안 필터 H(u,v)이고, 가운데는 실제 필터 마스크 이미지로 중앙이 밝고 주변으로 갈수록 어두워진다. 오른쪽은 다양한 $D_0$ 값에 따른 곡선으로 곡선이 오른쪽으로 갈수록( $D_0$ 값이 커질수록) 더 많은 고주파를 통과한다.

가장 우측이 가우시안 필터를 적용한 이미지이다. (b)이미지를 비교해보면 Butterworth보다 Ringing 현상이 훨씬 감소함을 확인할 수 있다.

Practical Applications of Lowpass Filtering

텍스트 이미지 복원

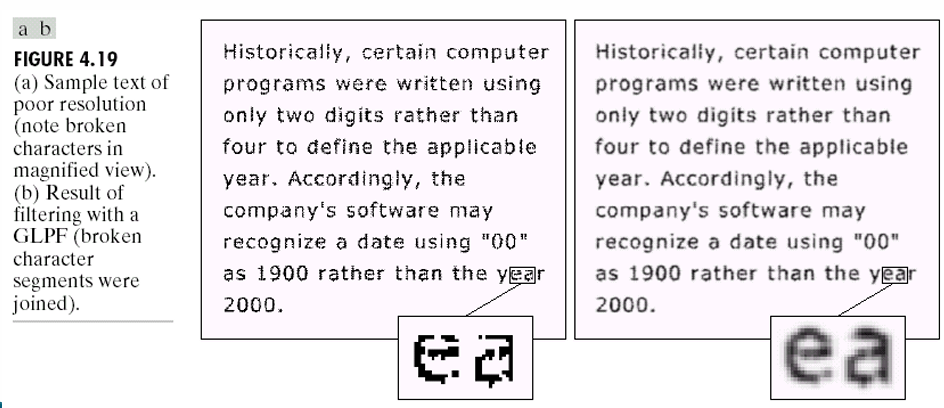
저해상도로 인해 글자 일부가 깨져보이는 이미지에서, 문자들의 단절된 부분을 부드럽게 연결해 가독성을 향상시킨다.

위 이미지에서는 Gaussian Lowpass Filter를 적용한 결과 깨져보이는 'e'와'a'가 필터링 후 연결된 'ea'로 복원된 모습이다.

인물 사진의 피부 질감 개선

인물 사진에서 세밀한 피부 질감(잔주름, 모공 등)을 줄이기 위해 사용된다.
Gaussian Lowpass Filter(GLPF)를 적용하면 $D_0$ 값에 따라 피부의 섬세한 선들이 부드럽게 되어, 좀 더 매끈한 피부 표현이 가능해진다. 뷰티필터 효과처럼 고주파 성분(잡티, 잔선)을 제거하여 시각적으로 부드럽고 선명한 느낌을 준다.

위성 영상의 스캔라인 제거

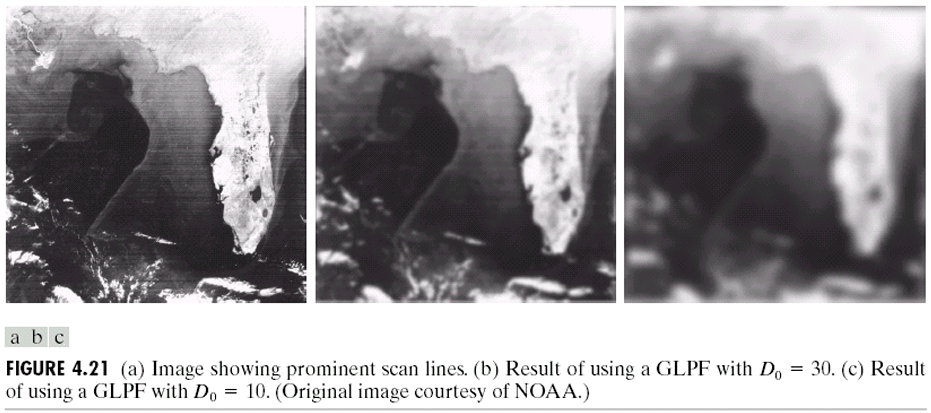
위성 영상 촬영 중 발생하는 수직/수평 스캔라인(주기적 노이즈)을 제거하는 데 사용된다.

동일하게 GLPF를 적용하면 $D_0$ 에 따라 주기적인 라인이 점차 사라지고 자연스러운 해양 및 지형 이미지로 개선된다.

정밀한 지형 분석이나 영상 해석을 위해 불필요한 인공 노이즈 제거가 중요하며, 저역 통과 필터는 효과적인 방법이다.

정리하면, 저역 통과 필터(Lowpass Filters)는 노이즈 제거 및 부드럽게 하기(smoothing), 고주파 성분 억제를 통한 디테일 감소(블러링), 스캔라인 등 주기적 패턴 제거, 글자, 문서, 위성, 인물 이미지 등 다양한 응용이 가능하다.

또한 필터의 종류(Ideal, Butterworth, Gaussian)에 따라 성능과 부작용(예: Ringing)의 정도가 다르므로, 적절한 필터 선택이 중요하다.

References

Images from Rafael C. Gonzalez and Richard E.
Wood, Digital Image Processing, 2nd Edition.

Yeontachi

기초를 다지는 중입니다.📚🧑‍💻

이전 포스트

[CV] Filtering in the Frequency Domain(1) - Frequency Domain

다음 포스트