[CV] Image Transformation(2) - 2D Transformation

Yeontachi·2025년 8월 20일

Computer Vision Note

목록 보기

33/47

영상 처리와 컴퓨터 비전에서 2D 변환(2D Transformation)은 두 영상이나 객체를 서로 정합(Alignment)하거나 새로운 좌표계로 표현할 때 기본적으로 사용되는 도구이다. 정합은 대응되는 점들을 가장 잘 설명하는 변환 모델을 찾는 문제로 이해할 수 있으며, 이러한 변환은 보통 전역 파라미터(Global Parametric Warping)로 정의된다.

2x2 행렬만으로도 회전(Rotation), 크기 변환(Scaling), 전단(Shear), 반사(Reflection) 같은 선형 변환을 표현할 수 있다. 하지만 이동(Translation)은 행렬곱만으로는 불가능하기 때문에, 이를 포함하기 위해 동차 좌표계(Homogeneous Coordinates)가 도입된다. 이때 좌표를 3차원 형태로 확장하고 3x3 행렬을 사용하면 선형 변환과 이동을 모두 포함하는 일반적인 변환을 표현할 수 있다.

기본적인 2D 변환에는 확대/축소, 회전, 이동, 전단, 반사 등이 있으며, 이들을 조합한 것이 Affine Transformation이다. Affine Transformation은 직선성을 보존하면서도 다양한 형태 변화를 허용하기 때문에 영상 정합에서 자주 사용된다.

결국, 2D 변환은 영상에서 대응점을 맞추고 두 장면을 하나로 결합하거나 특정 좌표계를 기준으로 이미지를 재표현하기 위한 수학적 기반이라고 할 수 있다.

Alignment as Fitting

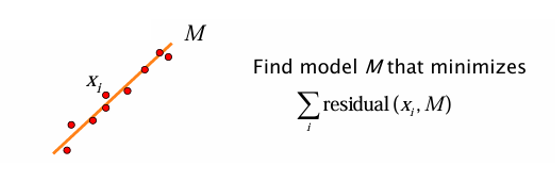
기존에는 한 장의 이미지 안에서 특정한 모델 $M$ 을 특징점들(feature points)에 맞추는 (fitting) 문제를 다뤘다.

예를 들어 여러 점들이 있을 때, 이 점들을 가장 잘 설명하는 직선 모델 $M$ 을 찾는 방식이였다. 이 과정은 잔차(residual), 즉 모델과 점들 간의 차이를 최소화하는 방향으로 이루어진다.

반면, 정합(Alignment)에서는 서로 다른 두 이미지가 있고, 각각의 이미지에서 추출된 특징점 쌍 $(x_i, x'_i)$ 이 주어진다.

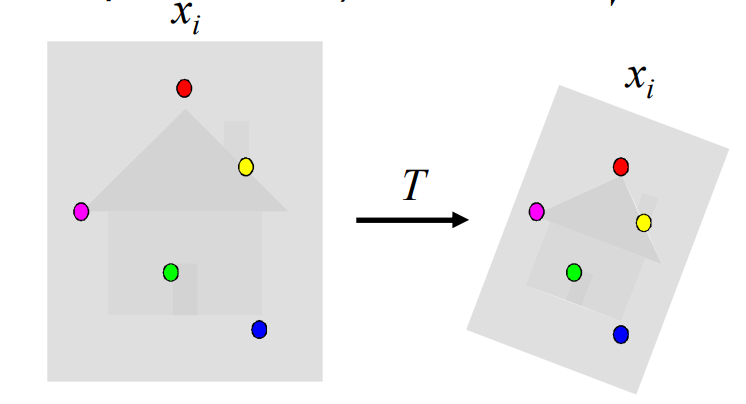
여기서 목표는 한 이미지의 점들을 다른 이미지의 대응점에 가장 잘 맞추는 변환(Transformation) $T$ 를 찾는 것이다.

즉,

\sum_i\text{residual}(T(x_i), x'_i)

를 최소화하는 $T$ 를 찾는 문제이다.

모델 피팅(Model Fitting) : 한 이미지 안에서 특징 점 $\to$ 모델(예: 직선)에 맞추는 것
정합(Alignment) : 두 이미지 간 대응 특징점 쌍 $\to$ 변환(예: 아핀, 호모그래피)에 맞추는 것

Parametric (Global) Warping

Warping은 이미지를 변환(transformation)하는 과정으로, 픽셀 좌표 $(x,y)$ 를 새로운 좌표 $(x',y')$ 로 사상(mapping)하는 것이다. 여기서 parametric이라는 말은 이 변환이 소수의 파라미터(parameters)로 정의될 수 있다는 뜻이며, global이라는 말은 이미지 전체에 동일하게 적용된다는 의미이다. 즉, 한 점에서 정의된 변환이 이미지의 모든 픽셀에 동일하게 작용한다.

수학적 표현

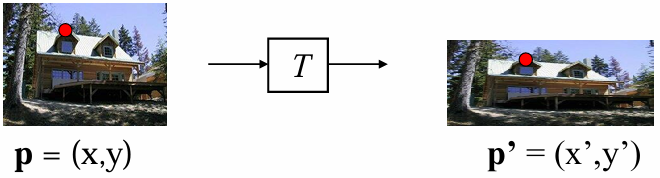
변환 $T$ 는 좌표 변환기와 같으며

p' = T(p)

형태로 표현된다.
이를 행렬 곱(matrix multiplication)으로 나타낼 수 있다.

\begin{bmatrix} x' \\ y' \end{bmatrix} = M \begin{bmatrix} x \\ y \end{bmatrix}

여기서 $M$ 은 변환을 정의하는 행렬이며, 이 행렬의 형태에 따라 변환이 이동/회전/스케일/아핀/투영으로 나뉜다.

핵심은, Global Parametric Warping은 이미지의 모든 점에 동일하게 적용되는 변환이며, 몇 개의 파라미터만으로 전체 변환을 기술할 수 있다는 점이다.

Scaling (확대 및 축소)

Scaling은 물체의 크기를 조절하는 변환이다. 좌표의 각 성분을 일정한 배율(scalar)로 곱하여 크기를 변화시키며, 이 과정에서 물체의 형태는 유지되지만 크기만 변한다.

Scaling은 크게 두 가지 방식으로 나눌 수 있다.

Uniform Scaling은 모든 좌표 성분에 동일한 배율을 적용하여 물체의 가로와 세로 비율을 그대로 유지하면서 크기만 변화시키는 방식이다.
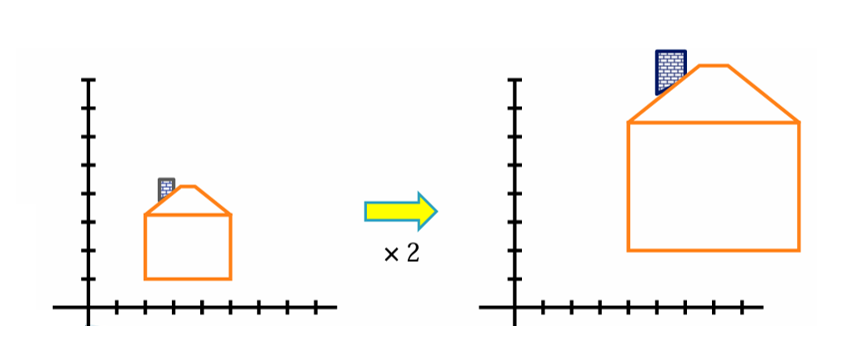
Non-Uniform Scaling은 각 성분에 서로 다른 배율을 적용하여 물체의 형태가 가로 혹은 세로 방향으로 늘어나거나 줄어드는 방식이다.
- 수학적 표현은 다음과 같다. $x' = ax, \quad y' = by$
- 여기서 a와 b는 각각 x축과 y축 방향의 배율을 의미한다. 이를 행렬 형태로 나타내면 다음과 같다. $\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$
- 즉, Scaling은 좌표에 단순한 곱셈 연산을 적용하여 크기를 변화시키는 기초적인 선형 변환이며, 다른 복잡한 2D 변환들의 기반이 된다.

What Transformations Can Be Represented with a 2x2 Matrix?

2D 공간에서 다양한 선형 변환들은 2x2 행렬을 통해 표현할 수 있다. 이 행렬은 점 $(x,y)$ 를 새로운 점 $(x', y')$ 로 매핑하며, 기하학적 구조를 바꾸는 역할을 한다.

2D Scaling(크기 조정)
각 좌표에 스케일 값을 곱하여 객체를 확대 또는 축소한다.
- Uniform scaling : 모든 축에 동일한 비율을 적용
- Non-Uniform scaling : 축마다 다른 비율 적용
  
  $x' = s_x \cdot x, \quad y' = s_y \cdot y$
  - Matrix form:
  $\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$
2D Rotation(회전)
원점을 중심으로 일정한 각도 $\theta$ 만큼 회전시키며, 코사인과 사인 항으로 표현된다.
$x' = \cos\theta \cdot x - \sin\theta \cdot y, \quad y' = \sin\theta \cdot x + \cos\theta \cdot y$

\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}

2D Shear(전단 변환)
한 축의 방향으로 기울이는 변환으로, 사각형을 평행사변형으로 만든다. $x' = x + sh_x \cdot y, \quad y' = sh_y \cdot x + y$

\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & sh_x \\ sh_y & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}

2D Reflection(대칭 변환)
축이나 원점을 기준으로 좌표를 반전시킨다. 예를 들어 Y축 대칭은 x를 음수로 바꾼다.
- Mirror about Y-axis:
  $x' = -x, \quad y' = y$ $\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$
- Mirror over (0,0):
  $x' = -x, \quad y' = -y$ $\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$

이러한 변환들은 모두 2x2 선형 변환 행렬로 표현이 가능하다. 하지만, Translation(평행 이동)과 같은 변환은 단순 2x2 행렬로는 표현할 수 없으며, 이 경우에는 동차 좌표(Homogeneous Coordinates)를 사용해 3x3 행렬로 확장해야 한다.

Homogeneous Coordinates

2차원 좌표계에서 우리는 보통 한 점을 $(x,y)$ 로 표현한다. 하지만 이러한 표현만으로는 모든 변환을 행렬 연산으로 표현하기 어렵다. 특히 Translation(이동) 같은 연산은 단순한 2x2 행렬 곱으로는 나타낼 수 없다. 이 문제를 해결하기 위해 Homogeneous Coordinate(동차 좌표계) 개념이 사용된다.

Homogeneous Coordinates로의 변환

일반적인 2D 좌표 $(x,y)$ 는 동차 좌표계에서 3차원 벡터로 확장된다. 즉,

(x, y) \;\;\Rightarrow\;\; \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}

이렇게 세 번째 성분을 추가함으로써, 단순한 2x2 행렬 연산으로 표현할 수 없었던 변환도 행렬 곱으로 나타낼 수 있게 된다.

Homogeneous Coordinates에서 다시 변환

동차 좌표계의 점은 $(x,y,w)$ 형태를 갖는다. 이때 원래의 2차원 좌표로 변환하려면 $w$ 로 나누어 주면 된다.

\begin{bmatrix} x \\ y \\ w \end{bmatrix} \;\;\Rightarrow\;\; \left( \frac{x}{w}, \frac{y}{w} \right)

즉, Homogeneous 좌표에서 스케일은 중요하지 않고, 좌파ㅛ의 비율만이 실제 점의 위치를 결정한다.

Translation을 Homogeneous Coordinates로 표현

앞서 언급했듯이, 이동 변환은 단순한 2x2 행렬로 표현할 수 없다. 하지만 Homogeneous Coordinates를 사용하면 이를 3x3 행렬로 깔끔하게 표현할 수 있다.

2차원 평면에서 이동은 다음과 같다.

x' = x + t_x \\ y' = y + t_y

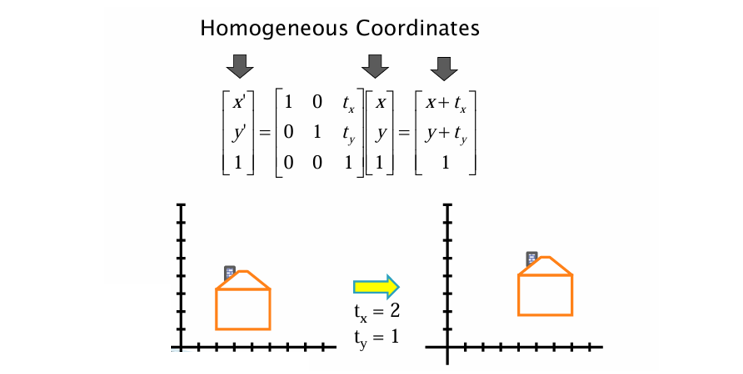
이를 Homogeneous 좌표계에서는 다음과 같은 행렬 곱으로 나타낼 수 있다.

Translation = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix}

즉, 단순히 행렬의 마지막 열에 이동 벡터 $(t_x, t_y)$ 를 추가하는 것만으로도 이동 변환을 행렬 연산으로 표현할 수 있다.

Homogeneous Coordinates의 장점

통합된 표현 : 회전(Rotation), 스케일링(Scaling), 이동(Translation), 기하학적 변환을 모두 행렬 곱으로 일관되게 표현할 수 있다.
계산의 단순화 : 여러 변환을 연속적으로 적용할 때, 각각의 변환 행렬을 곱하기만 하면 된다.
확장성 : 2D뿐만 아니라 3D 컴퓨터 그래픽스에서도 필수적으로 사용된다.

즉, Homogeneous Coordinates는 행렬 곱만으로 모든 기하학적 변환을 처리할 수 있게 하는 좌표계 확장 방법이다.

Basic 2D Transformations with Homogeneous Coordinates

1. Translation (이동)
이동은 한 점 $(x, y)$ 을 $(t_x, t_y)$ 만큼 평행 이동시키는 연산이다.

x' = x + t_x, \quad y' = y + t_y

이를 Homogeneous 좌표계로 표현하면 다음과 같다.

\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}

2. Scaling(스케일링)
스케일링은 좌표를 특정 배율로 확장하거나 축소하는 변환이다.

x' = s_x \cdot x, \quad y' = s_y \cdot y

Homogeneous 행렬 표현은 다음과 같다.

\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}

3. Rotation(회전)
회전은 원점을 기준으로 좌표를 $\theta$ 만큼 회전시키는 연산이다.

x' = \cos\theta \cdot x - \sin\theta \cdot y, \quad y' = \sin\theta \cdot x + \cos\theta \cdot y

Homogeneous 행렬 표현은 다음과 같다.

\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}

4. Shear(시어, 전단 변환)
시어는 축 방향으로 좌표를 기울이는 변환이다.

x' = x + sh_x \cdot y, \quad y' = sh_y \cdot x + y

Homogeneous 행렬 표현은 다음과 같다.

\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & sh_x & 0 \\ sh_y & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}

Homogeneous Coordinates를 활용하면 2D 기하학적 변환을 3×3 행렬 곱으로 일관되게 표현할 수 있다.

Translation: 행렬 마지막 열에 이동 벡터 추가
Scaling: 대각 성분에 배율 적용
Rotation: 삼각함수 기반 회전 행렬
Shear: 비대각 성분에 기울임 계수 추가

이러한 통합적 표현 덕분에, 여러 변환을 순차적으로 적용할 때는 각 변환 행렬을 곱해 하나의 복합 변환 행렬로 표현할 수 있다. 이는 컴퓨터 그래픽스, 비전, 로보틱스에서 변환을 효율적으로 처리할 수 있게 해준다.

2D Affine Transformations2D

아핀 변환(Affine Transformation)은 영상 및 기하학적 데이터 처리에서 가장 널리 쓰이는 선형 변환의 한 형태이다. 아핀 변환은 직선성(linearity)과 평행성(parallelism)을 보존하지만, 길이와 각도는 일반적으로 보존하지 않는다. 즉, 변환 후에도 직선은 여전히 직선으로 유지되고 평행한 직선은 여전히 평행하게 남지만, 크기나 각도는 달라질 수 있다.

\begin{bmatrix} x' \\ y' \\ w' \end{bmatrix} = \begin{bmatrix} a & b & c \\ d & e & f \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ w \end{bmatrix}

2D Affine Transformation은 선형 변환(Linear Transformations) + 이동(Translations)으로 구성된다.
직선과 평행성은 보존되지만, 길이나 각도는 일반적으로 보존되지 않는다.
동차 좌표를 사용하면 변환을 하나의 $3\times 3$ 행렬로 통합하여 계산할 수 있다.
스케일링, 회전, 전단, 평행 이동 모두 아핀 변환의 특수한 경우이다.