[CV] Image Transformation(3) - Transformation Fitting

Yeontachi·2025년 8월 20일

Computer Vision Note

목록 보기

34/47

Transformation Fitting은 두 영상 간의 대응점(correspondence)을 이용하여 가장 잘 맞는 변환(Transformation)을 추정하는 과정이다. 특히 영상 정합(Image Alignment)에서 자주 활용되며, 특징점 기반 매칭(SIFT, SURF 등)과 결합하여 아핀 변환, 투영 변환 등을 추정할 수 있다.

Alignment Problem

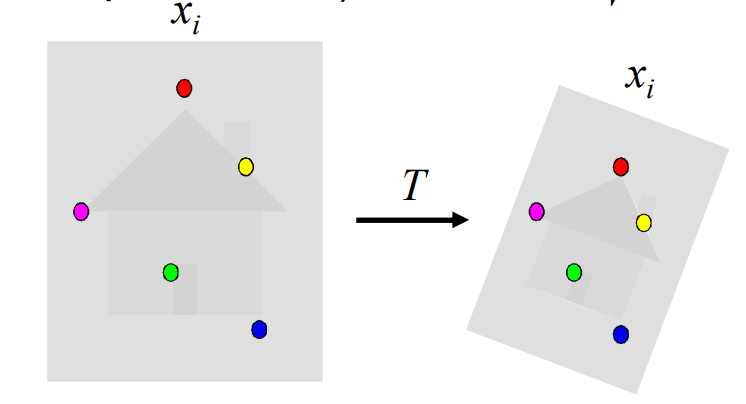
영상 정합(Alignment problem)은 두 영상에서 추출된 특징점(feature points)을 기반으로, 두 영상 사이의 변환 관계를 찾는 문제이다.

입력 : 두 영상에서 검출된 특징점 집합과 그 대응 관계(correspondence)
- 예를 들어, 왼쪽 영상의 $x_i$ 와 오른쪽 영상의 $x'_i$ 가 짝을 이룬다하면, 이 둘은 SIFT, SURF, ORB와 같은 로컬 특징 기술자(Descriptor)를 통해 얻을 수 있다.
목표 : 두 대응점 집합을 가장 잘 연결하는 변환 $T$ 를 찾는 것
- 즉, $x_i \overset{T}{\longrightarrow} x_i'$ 관계를 만족하는 $T$ 의 파라미터를 추정한다.
문제 제기 :
- 변환 $T$ 는 아핀 변환(Affine), 투영 변환(Projective/Homography), 혹은 단순 이동/회전/스케일링**일 수 있다.
- 따라서 문제는 "어떤 변환 모델을 가정하고, 그 모델의 파라미터를 어떻게 계산할 것인가?"로 귀결된다.

영상 정합은 두 영상이 동일한 장면을 표현할 때, 한 영상을 다른 영상과 공간적으로 맞추는 과정이다. 위 문제의 해결은 크게 두 가지 접근으로 나눌 수 있다.

1. Direct(Pixel-based) Alignment

아이디어: 영상의 픽셀 값 자체를 이용하여 정합을 수행한다.
방법 : 한 영상을 다른 영상에 맞추어 다양한 변환(이동, 회전, 스케일 등)을 적용해 보고, 픽셀 값의 유사도(예: SSD, NCC, Mutual Informatioin)가 최대가 되는 위치를 찾는다.
장점 : 별도의 특징 추출 과정이 필요 없으므로 모든 픽셀 정보를 활용 가능하다.
단점 : 계산량이 크고, 조명 변화나 잡음에 민감하다. 초기 위치가 크게 어긋나 있으면 수렴하지 않을 수 있다.

2. Feature-based Alignment

아이디어: 영상에서 특징점(feature points)을 먼저 추출한 후, 특징점들 사이의 대응 관계를 이용해 정합한다.
방법 :
1. 특징 검출(예: 코너, 블롭, SIFT, SURF, ORB 등)
1. 특징 기술자(descriptor)로 표현
2. 두 영상 간 매칭된 특징점 쌍을 찾음
3. 변환 모델(아핀, 호모그래피 등)을 추정
장점 : 조명 변화, 잡음, 가림(occlusion)에 강인하며, 계산량이 픽셀 기반보다 적다.
단점 : 특징 검출 및 매칭의 정확도에 의존한다.

실제 응용에서는 Feature-based alignment로 먼저 대략적인 변환을 구한 후, Direct alignment로 세밀하게 보정(refinement)하는 방식을 자주 사용한다.

예를 들어, SIFT로 초기 대응점 추출 $\to$ RANSAC 기반 아핀 변환 추정 $\to$ 이후 픽셀 기반 옵티마이제이션으로 미세 정합

Fitting an Affine Transformation

앞서 영상 정합(Image Alignment) 문제를 해결하기 위해 변환 모델이 필요한데, 그 중 가장 기본적이고 자주 활용되는 것이 아핀 변한(Affine Transformation)이다. 아핀 변환은 특징점 대응 관계를 기반으로 비교적 단순하게 계산할 수 있으며, 실제로 다양한 응용에서 안정적인 성능을 보여준다.

우선 아핀 변환의 장점은 간단한 피팅 절차(Simple fitting procedure)에 있다. 변환은 선형 방정식 형태로 표현되므로, 주어진 대응점들을 이용해 선형 최소자승법(linear least squares)을 적용하면 파리미터를 쉽게 추정할 수 있다. 즉, 여러 쌍의 대응점이 있을 때 이들을 모두 만족시키는 변환은 존재하지 않더라도, 최소자승법을 통해 전체적으로 오창가 가장 작은 근사해를 구할 수 있는 것이다. 이 과정은 계산적으로 효율적이고, 대응점이 많아질수록 안정성이 높아진다.

또한 아핀 변환은 뷰포인트 변화(viewpoint change)를 근사(approximate)할 수 있다는 점에서 실용적이다. 물론 아핀 변환은 본래 3차원 원근 투영을 완전히 표현할 수 있는 모델은 아니다. 하지만 물체가 대체로 평면적 구조(planer object)를 가지고 있고, 카메라가 정사영(orthographic)에 가까운 조건이라면, 실제로 발생하는 뷰포인트 변화를 상당히 잘 설명할 수 있다. 예를 들어, 서로 다른 시점에서 촬영된 장난감 트럭의 창문 부분을 생각해보면, 비록 3차원적인 위치 변화가 존재하더라도 창문이라는 평면 영역은 아핀 변환만으로도 충분히 일관되게 맞출 수 있다.

따라서 아핀 변환은 단순히 이론적인 모델이 아니라, 실제 영상 정합에서 빠르고 안정적인 첫 단계 모델로서 자주 활용된다. 복잡한 투영 변환이 필요한 경우에도, 초기 정합은 아핀 변환으로 시작하여 그 위에 더 정밀한 모델을 적용하는 방식이 일반적이다.

아핀 변환을 실제로 추정하기 위해서는 두 영상 간의 **대응점(correspondence) 집합이 필요하다. 예를 들어, 첫 번ㄹ째 영상에서 특징점이 $(x_i, y_i)$ 로 주어지고, 두 번째 영상에서 그에 대응하는 점이 $(x'_i, y'_i)$ 라고 하자. 목표는 이 두 점을 연결하는 변환 파라미터를 추정하는 것이다.

아핀 변환은 다음과 같이 표현된다.

\begin{bmatrix} x'_i \\ y'_i \end{bmatrix} = \begin{bmatrix} m_1 & m_2 \\ m_3 & m_4 \end{bmatrix} \begin{bmatrix} x_i \\ y_i \end{bmatrix} + \begin{bmatrix} t_1 \\ t_2 \end{bmatrix}

여기서 추정해야 할 미지수는 총 6개, 즉 $(m_1, m_2, m_3, m_4, t_1, t_2)$ 이다.

1. 선형 방식으로 전개

위 식을 전개하면 다음과 같이 선형 방정식의 형태를 얻을 수 있다.

x'_i = m_1 x_i + m_2 y_i + t_1

y'_i = m_3 x_i + m_4 y_i + t_2

즉, 대응점 한 쌍은 두 개의 독립적인 방정식을 제공한다.

2. 행렬 형태로 표현

여러 대응 점을 하나의 행렬 형태로 정리하면, 아래와 같이 표현된다.

\begin{bmatrix} x_i & y_i & 0 & 0 & 1 & 0 \\ 0 & 0 & x_i & y_i & 0 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \end{bmatrix} \begin{bmatrix} m_1 \\ m_2 \\ m_3 \\ m_4 \\ t_1 \\ t_2 \end{bmatrix} = \begin{bmatrix} x'_i \\ y'_i \\ \vdots \end{bmatrix}

이렇게 하면 문제는 단순한 선형 시스템으로 환원된다.

3. 대응점의 개수와 해법

아핀 변환 파라미터는 총 6개이므로, 최소 3쌍의 대응점(=6개의 방정식)이 있으면 해를 구할 수 있다.

만약 대응점이 3쌍보다 많다면, 일반적으로 모든 방정식을 정확히 만족시키는 해는 존재하지 않는다. 이 경우 최소승자법(Least Squares)을 이용해 오차가 최소가 되는 근사 해를 구한다.

Transformation Fitting Process Examples

1. 특징점 추출과 기술(Feature Detection & Description)
두 영상에서 먼저 관심점(Interest points)을 검출한다. SIFT는 이미지의 크기 변화(Scale)와 회전(rotation)에 불변하도록 설계되어, 서로 다른 시점에서 찍은 영상이라도 안정적으로 특징점을 찾을 수 있다.

왼쪽부터, 원본 영상, 특징점과 그 크기, 방향을 나타낸 영상, 각 특징점을 Descriptor 벡터로 표현한 영상이다.

즉, 영상에서 단순히 점을 찍는 것이 아니라, 주변 지역의 구조적 패턴(gradient 분포)을 고차원 벡터로 변환해 "이 점이 어떤 점인지"를 설명한다.

2. 특징 매칭(Feature Matching)
서로 다른 두 영상에서 검출된 SIFT Descriptor는 유사도를 비교하여 대응쌍(correspondence pairs)을 형성한다.

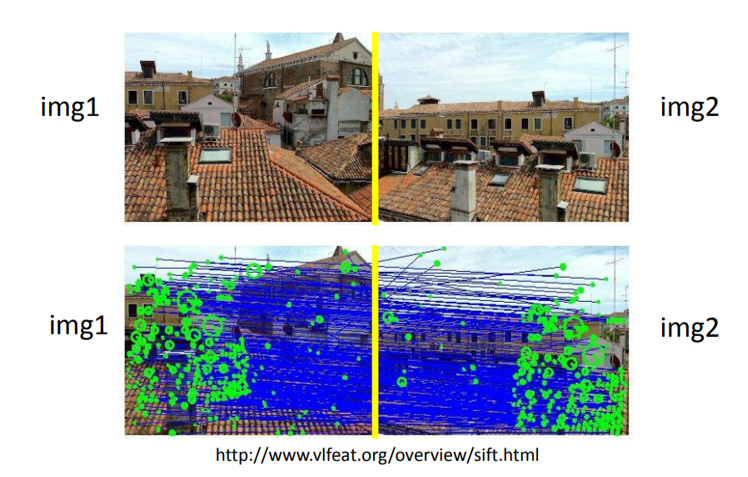
위 그림처럼 두 영상에서 수백 개의 SIFT 특징점이 검출되고, 이들 중 비슷한 Descriptor끼리 연결되어 초기에 많은 대응쌍이 만들어진다.

하지만 여기에는 잘못된 매칭도 포함되므로, 이후 변환 추정 과정에서 이를 걸러내는 과정(RANSAC 등)이 필요하다.

3. 아핀 변환 추정(Affine Transformation Estimation)
대응쌍이 준비되면 이제 이를 기반으로 변환을 추정한다. 아핀 변환은 다음과 같이 표현된다.

\begin{bmatrix} x'_i \\ y'_i \end{bmatrix} = \begin{bmatrix} m_1 & m_2 \\ m_3 & m_4 \end{bmatrix} \begin{bmatrix} x_i \\ y_i \end{bmatrix} + \begin{bmatrix} t_1 \\ t_2 \end{bmatrix}

여기서 $(m_1, m_2, m_3, m_4)$ 는 선형 변환 계수, $t_1, t_2$ 는 평행이동(translation) 성분이다. 즉, 대응쌍을 많이 확보할수록 선형 방정식 시스템을 구성할 수 있고, 이를 최소자승법(linear least squares)으로 풀어 최적의 아핀 변환을 구할 수 있다.