두 영상 사이에서 특징점을 매칭할 때, 앞서 본 것처럼 모든 대응쌍이 올바른 매칭은 아니다. 실제 매칭 결과에는 많은 오류 대응쌍(Outlier)이 포함되며, 이는 변환 추정에 큰 영향을 미친다.
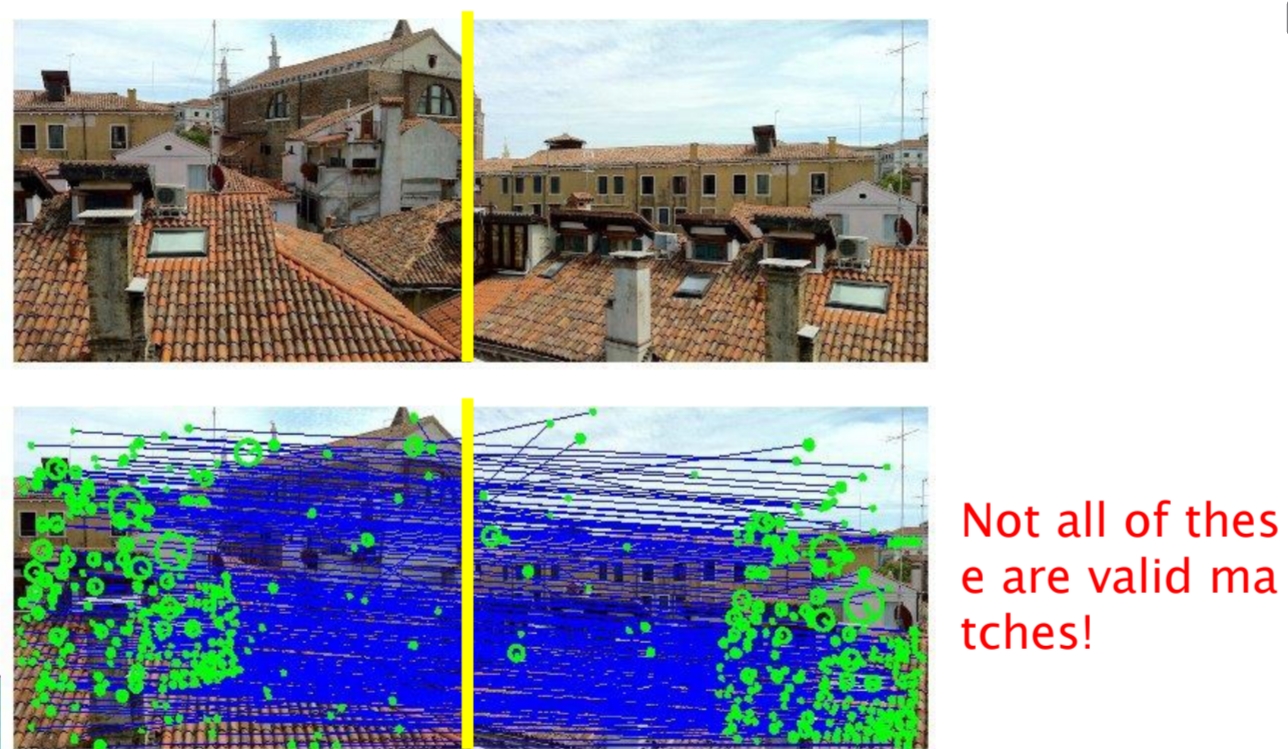
예를 들어, 두 장의 건물 이미지에서 SIFT를 통해 수많은 매칭 쌍이 검출되었지만, 아래 그림처럼 일부는 잘못 연결된 것이다. 이러한 잘못된 대응점이 그대로 포함된다면, 아핀 변환이나 호모그래피 같은 파라미터 추정 과정에서 결과가 크게 왜곡된다.
Outlier란,
두 이미지에서 잘못 매칭된 점 쌍(erroneous pair of matching points) 또는 잡음(noise)이나 실제 모델(예: 직선, 평면)에 속하지 않는 점을 의미한다.
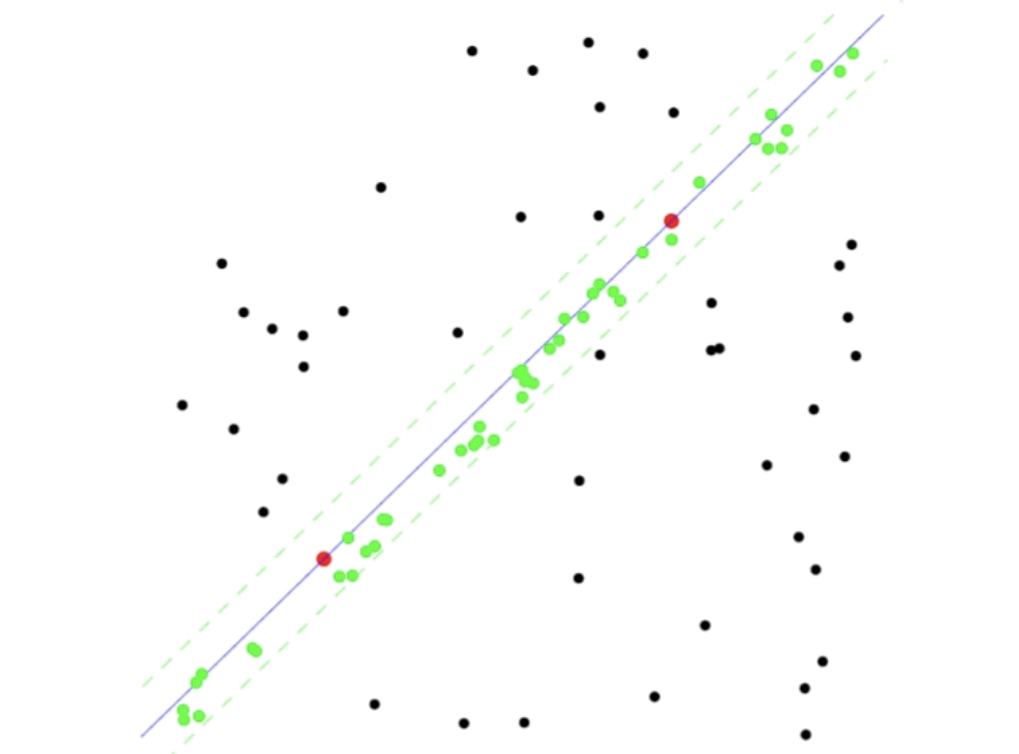
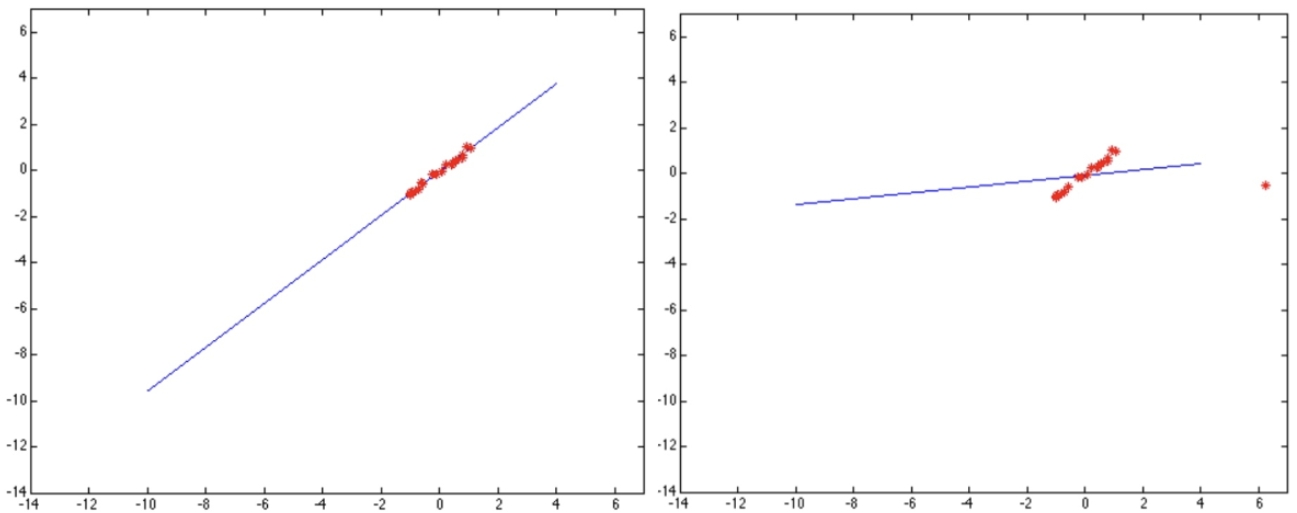
그림 예시처럼, 대부분의 점이 직선 위에 잘 위치할 때는 올바른 모델이 추정된다. 하지만 한 개의 outlier만 포함되어도 직선이 크게 틀어져 잘못된 결과를 만들 수 있다. 이는 이미지 정합뿐 아니라, 직선/평면 피팅, 모션 추정 등 다양한 비전 문제에서 발생한다.
따라서, outlier를 제거하지 않고 단순히 최소자승법(least squares)을 사용하면, 모델 추정은 불안정해지고 신뢰할 수 없게 된다. 이를 해결하기 위해 등장한 방법이 바로 RANSAC(Random Sample Consensus)이다.

RANSAC은 데이터 안에 다수의 outlier가 존재하더라도, 반복적인 샘플링과 모델 검증 과정을 통해 outlier에 강인한(robust) 추정을 가능하게 한다. 즉, 전체 데이터를 무조건 사용하는 대신, 랜덤하게 소수의 점을 선택하여 모델을 피팅하고, 그 모델을 지지하는 점들을 세어 최적의 해를 찾는 방식이다.
RANSAC(Random Sample Consensus)
영상 정합(Image Alignment)이나 직선 피팅과 같은 문제에서 가장 큰 난제는 Outlier의 존재이다. 단순 최소자승법(Least Squares)으로 모델을 추정하면, 소수의 잘못된 점들이 전체 결과를 왜곡시킨다. 따라서 우리는 Outlier의 영향을 최소화하고, 진짜 해(모델)를 지지하는 Inlier만을 활용하는 방법이 필요하다. 이를 가능하게 하는 기법이 바로 RANSAC(Random Sample Consensus)이다.
기본 아이디어
- RANSAC은 전체 데이터에서 일부를 무작위로 뽑아(seed group) 임시 모델을 만든다.
- 만들어진 모델에 대해, 얼마나 많은 데이터가 그 모델을 지지하는지 확인한다. 이때 모델과 잘 맞는 점들을 Inliers, 그렇지 않은 점들을 Outliers라고 부른다.
- Inlier 수가 충분히 많다면, 이 점들을 기반으로 다시 정교한 모델을 추정한다.
- 이 과정을 여러 번 반복하여, 가장 많은 Inlier를 포함하는 모델을 최종 해로 선택한다.
Intuition
만약 Outlier만으로 모델을 피팅하면, 결과는 다른 점들의 지지를 거의 받지 못한다. 반대로 Inlier를 중심으로 모델을 만든다면, 다수의 점들이 이 모델을 지지하게 되고, 반복적인 샘플링 끝에 올바른 해에 도달할 수 있다. 즉, Outlier는 다수의 합의(consensus)를 얻지 못하기 때문에 자연스럽게 배제된다.
RANSAC for Line fitting Example
1. 데이터 분포 확인
아래 그림처럼, 점들이 전체적으로 분포해 있지만 그중 일부는 특정 직선 패턴(대각선 방향)에 잘 정렬되어 있다. 하지만 데이터에는 잡음과 Outlier가 많기 때문에 단순 Least Squares Fit으로는 올바른 모델을 잡아내기 어렵다.
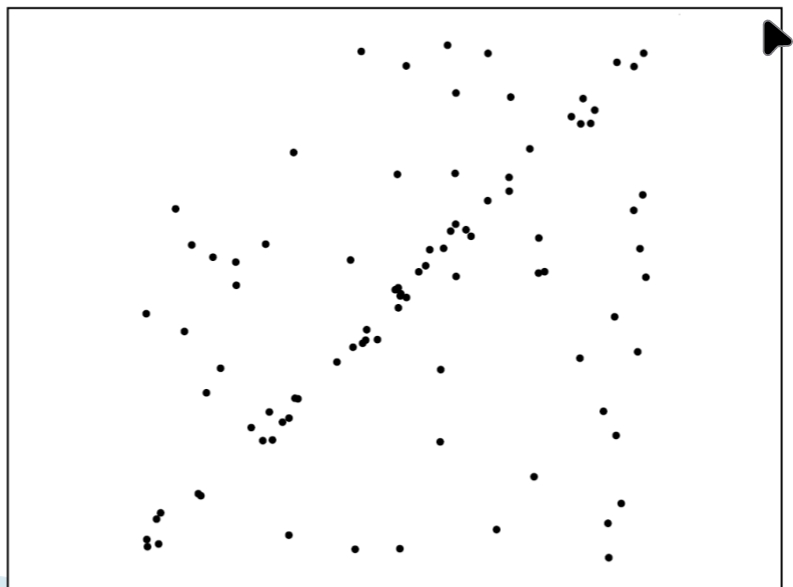
2. 무작위 샘플링(Random Sampling)
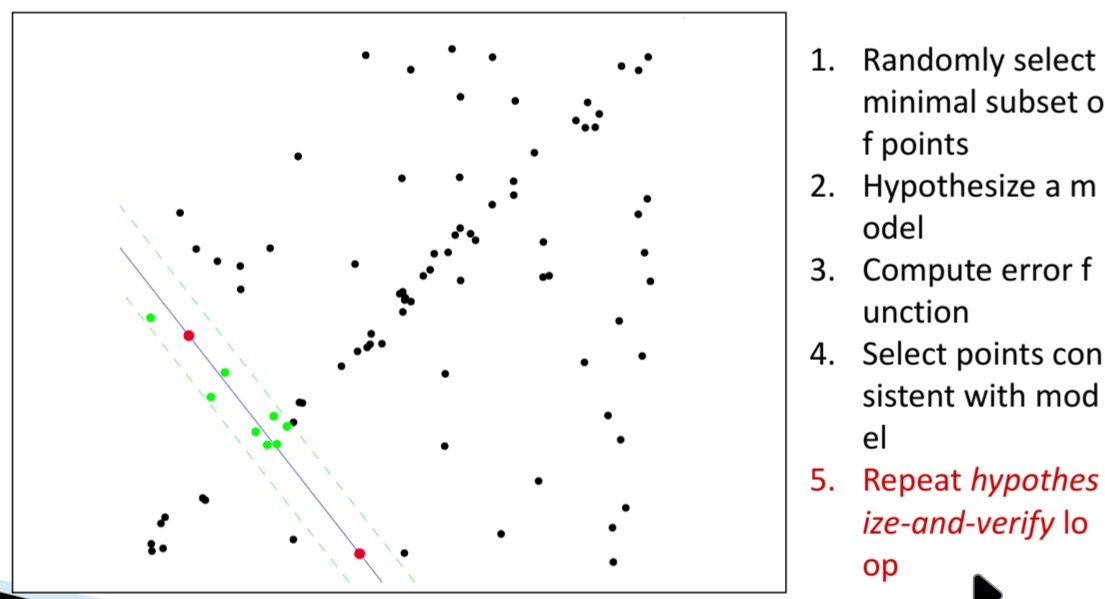
RANSAC은 전체 데이터에서 최소 샘플 집합(minimal subset)을 무작위로 선택한다.
예를 들어 직선을 정의하려면 2개의 점만 있으면 충분하다. 그림에서 빨간 점 두 개가 이 샘플을 의미한다.
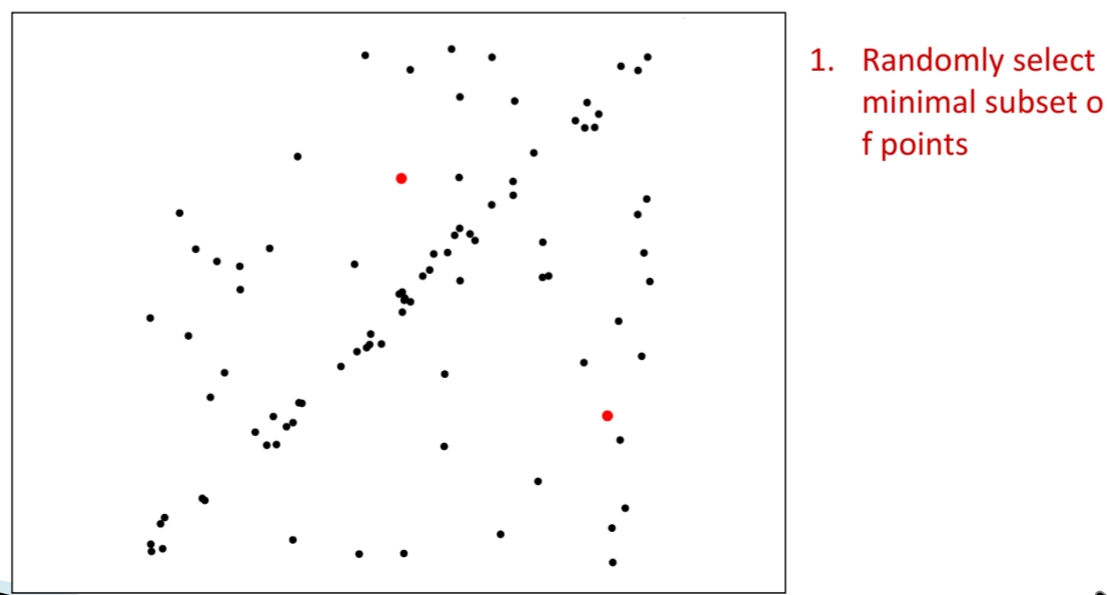
3. 가설 모델 추정(Hypothesize a Model)
선택된 두 점을 이용해 직선(가설 모델, 파란 선)을 만든다. 이 직선이 얼마나 데이터를 잘 설명하는지는 아직 알 수 없으므로, 다음 단계에서 평가한다.
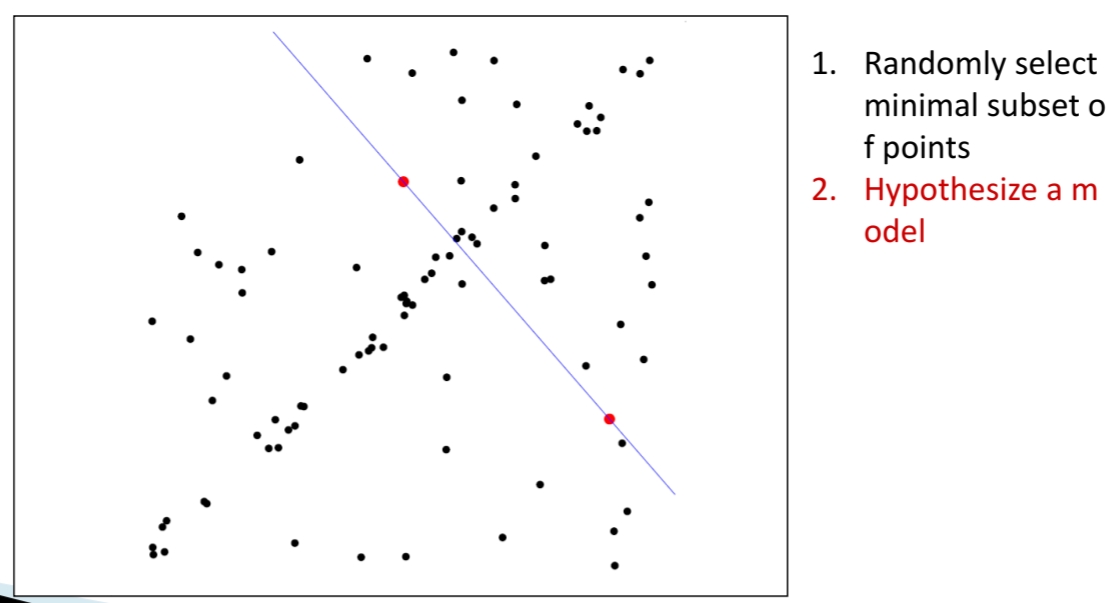
4. 오차 계산 및 Inlier 탐색(Compute Error Funtion & Inlier Selection)
전체 데이터에 대해, 각 점과 추정된 직선까지의 거리를 계산한다.
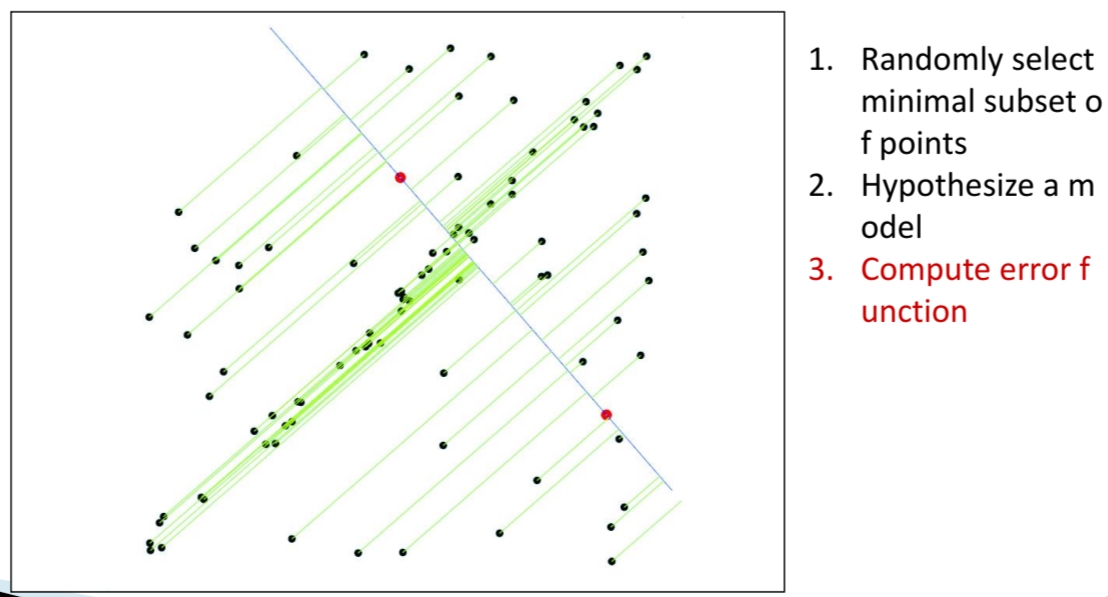
거리가 특정 임계값(threshold) 이하이면 Inlier(모델을 지지하는 점, 초록색), 크면 Outlier(지지하지 않는 점, 검은색)로 분류한다.
아래 그림에서 보듯 직선 주변 일정 거리 안에 있는 점들이 Inlier로 선택된다.
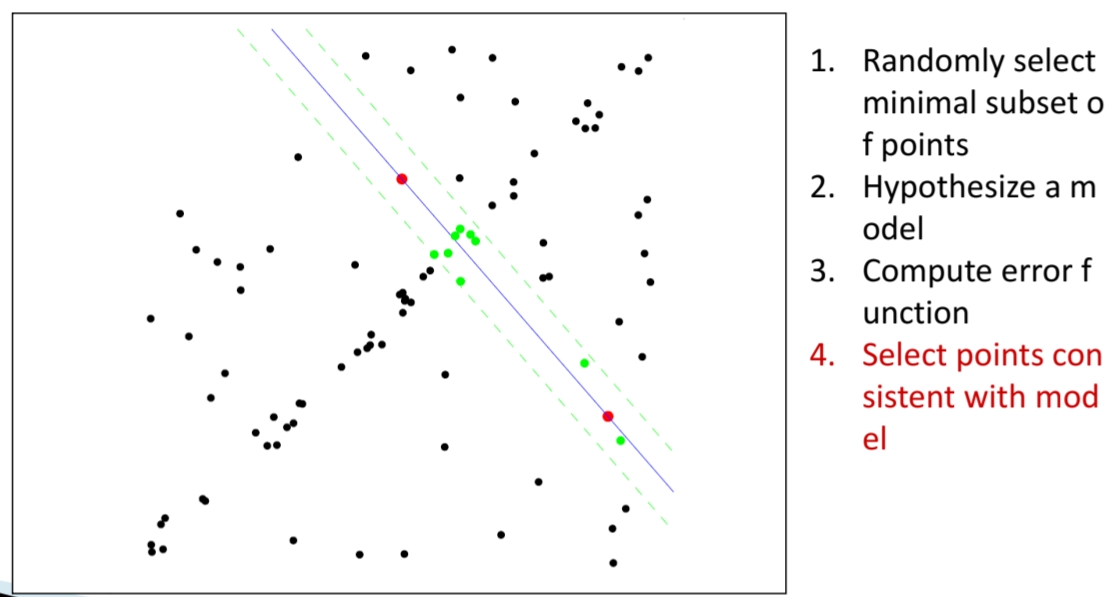
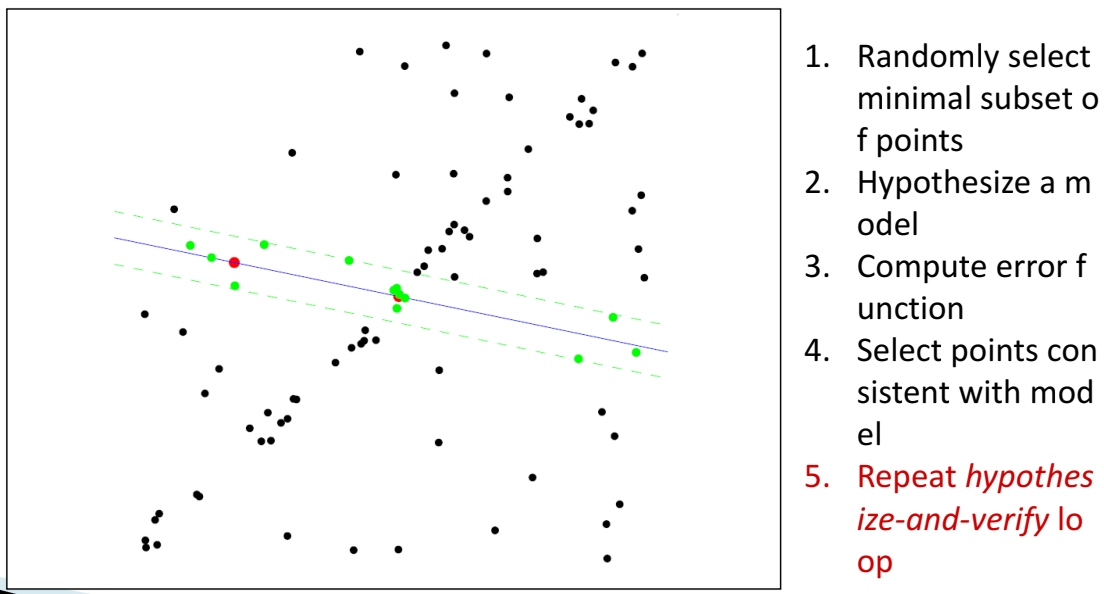
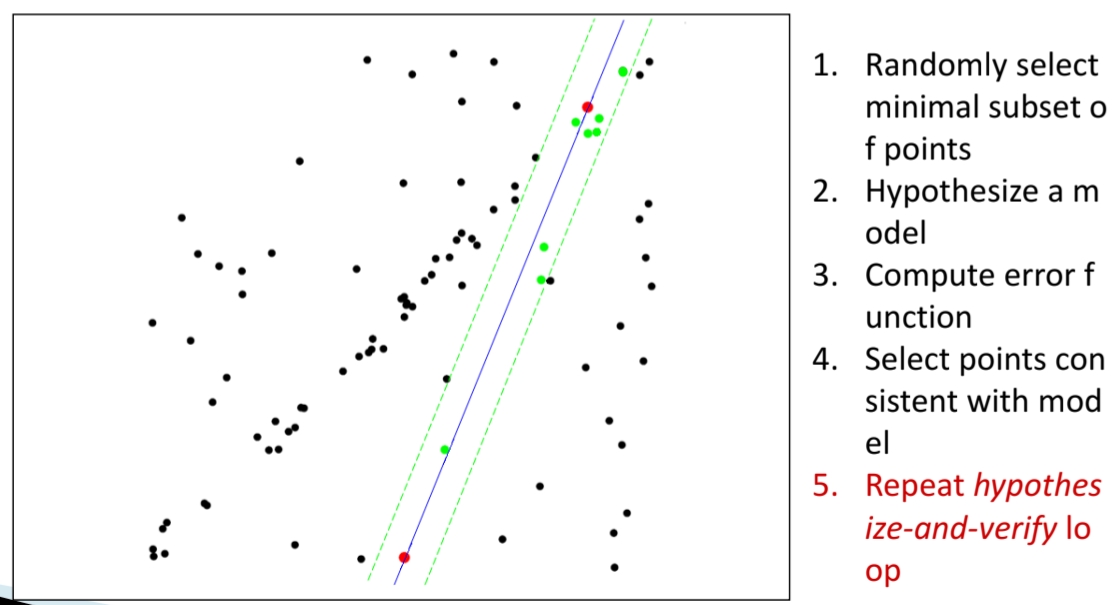
5. 반복(Hypothesize-and-Verify Loop)
위 과정을 여러 번 반복하면서, 무작위 샘플링으로 다양한 직선을 추정한다. 매번 Inlier 수를 계산해, 가장 많은 Inlier를 지지받는 모델을 찾는다.
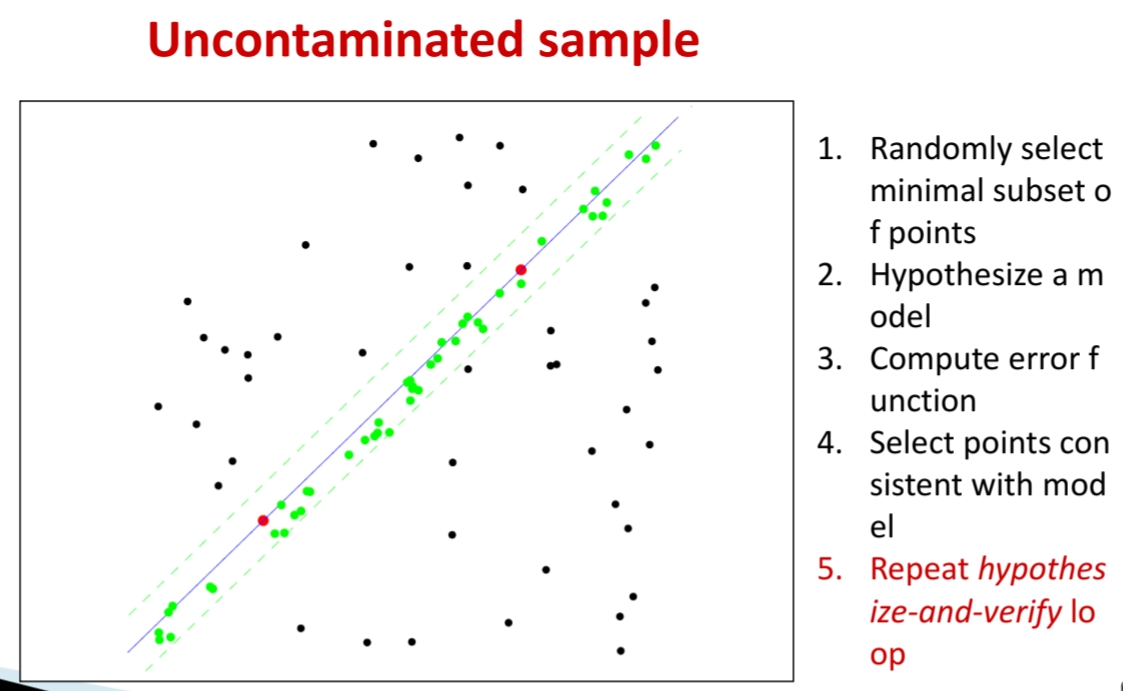
"Uncontaminated sample" 그림처럼, 올바른 샘플이 뽑히면 직선이 Inlier 집합을 잘 설명하게 된다.
RANSAC 반복 횟수
RANSAC은 무작위 샘플링(Random Sampling)에 기반하기 때문에, 매번 뽑은 샘플이 전부 Inlier일 확률이 보장되지 않는다. 따라서 충분히 많은 횟수를 반복해야 Outlier 없이 "순수한 샘플"을 얻을 수 있다.
수식은 아래와 같다.
- : 한 점이 Inlier일 확률
- : 모델을 추정하는 데 필요한 샘플의 최소 개수(예: 직선 = 2점, 아핀 변환 = 3점, 호모그래피 = 4점)
- : 전체 반복 후 성공할 확률(즉, 적어도 한 번은 모든 샘플이 Inlier일 확률)
- : 반복 횟수(Trials)
이때, 한 번의 시도에서 뽑힌 k개 점이 전부 Inlier일 확률은
반대로, 한 번의 시도가 실패할 확률은
그러면, S번의 모든 시도가 실패할 확률은
따라서 S번 중 적어도 한 번은 성공할 확률은
성공 확률 를 보장하기 위해 필요한 최소 반복 횟수는 다음과 같이 계산된다.
즉, 원하는 성공 확률 (예: 0.99 이상)을 정하면, 그에 맞게 반복 횟수를 계산할 수 있다.
Summary
RANSAC은 단순히 무작위로 여러 번 시도하는 게 아니라,
성공 확률 을 보장할 만큼 충분히 많은 횟수 를 돌려야 Outlier에 영향을 받지 않고 안정적인 모델을 얻을 수 있다.
