[CV] Segmentation(1) - Thresholding

영상 분할(Segmentation)은 디지털 영상 처리에서 매우 핵심적인 단계로, 영상 속의 픽셀들을 의미 있는 영역이나 객체 단위로 나누는 과정을 말한다. 단순히 픽셀의 집합을 나누는 것이 아니라, 비슷한 성질을 가진 픽셀들을 묶어 동질적인 영역을 형성하고, 서로 다른 영역을 구분함으로써 이후의 고차원적 처리(예: 객체 인식, 장면 이해)를 용이하게 한다.

Segmentation의 목적은 크게 세 가지로 나눌 수 있다.

• 비슷한 속성을 가진 픽셀들을 하나의 덩어리로 묶어 객체나 영역을 형성한다.
  

• 이미지를 일관된 "대상"으로 분리한다. 즉, 수많은 픽셀로 이루어진 복잡한 영상을, 우리가 인지할 수 있는 독립적 단위(객체나 의미있는 영역)로 조직화한다.
  

• 원본 영상 전체를 다루는 대신, 유사한 픽셀을 하나의 단위로 묶어(superpixels) 연산 효율을 높인다.
  

접근 방식은 크게 두 가지이다.

• Bottom-up 접근 : 색상, 밝기, 질감 등 저수준(low-level)의 시각적 유사성에 따라 픽셀을 묶는다.
• Top-down 접근 : 특정 객체라는 전제 하에 해당 객체를 이루는 픽셀들을 그룹화 한다.

또한, 심리학적 관점에서 등장한 게슈탈트 원리(Gestalt principle) 역시 영상 분할과 밀접하다.

인간의 시각 시스템은 선의 연속성, 근접성, 유사성, 폐쇄성 등의 원리에 따라 서로 다른 요소들을 하나의 패턴이나 객체로 인식한다. 이러한 원리는 컴퓨터 비전의 분할 알고리즘 설계에도 영향을 미쳤다.

즉, Segmentation의 도입부에서는 영상 속 복잡한 픽셀 집합을 단순히 나누는 것이 아니라, 의미 있는 그룹으로 조직화하여 이해 가능한 구조로 만드는 과정이라는 점을 강조할 수 있다.

Thresholding

영상 분할(Segmentation)은 복잡한 영상을 의미 있는 영역으로 나누는 과정이며, 이 중 가장 직관적이고 널리 사용되는 기법이 바로 Thresholding(임계값 분할)이다.

Thresholding의 기본 아이디어는 단순하다. 영상의 각 픽셀 값을 하나의 임계값 $T$와 비요하여, 이 값보다 크면 객체(Object), 작거나 같으면 배경(Background)으로 분류하는 것이다. 즉, 픽셀의 밝기값(intensity)을 기준으로 객체와 배경을 구분하는 방식이다. 이때 보통 "밝은 객체, 어두운 배경"이라는 전제가 깔려 있다.

Thresholding은 수식으로 다음과 같이 표현된다.

여기서 $f(x,y)$는 원본 영상의 픽셀 값이고, $g(x,y)$는 분할된 영상의 픽셀 값이다.
$T$는 임계값이며, $a$와 $b$는 객체와 배경을 나타내는 값이다. 일반적으로 객체는 흰색(1), 배경은 검은색(0)으로 표시된다.

Thresholding은 단순하고 계산 속도가 빠르기 때문에 다양한 응용에서 핵심적인 역할을 한다. 그러나 단 하나의 임계값으로는 영상 전체를 잘 분리하기 어려운 경우가 많아, 여러 변형된 방법들이 등장했다.

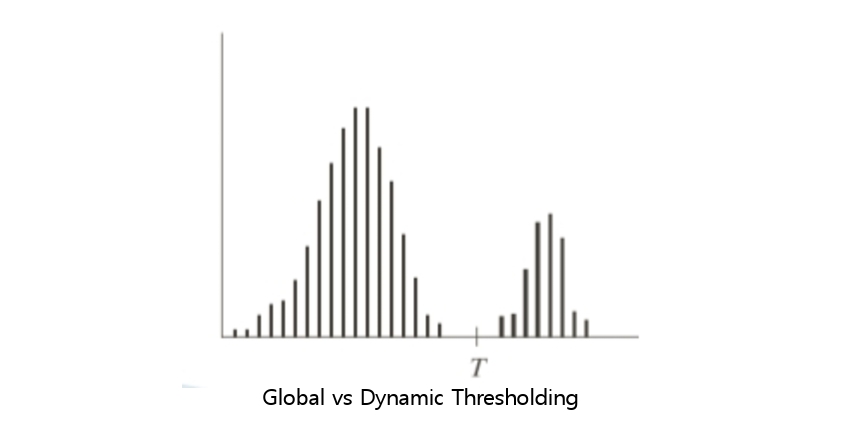
첫째, Global Thresholding(전역 임계값)은 영상 전체에 동일한 임계값을 적용하는 방식이다. 가장 단순하며 속도가 빠르다는 장점이 있지만, 조명 변화가 심하거나 배경이 균일하지 않은 경우에는 성능이 크게 떨어진다.

둘째, Dynamic 또는 Adaptive Thresholding(적응형 임계값)은 영상의 지역적 특성을 고려하여 임계값을 다르게 적용하는 방식이다. 각 픽셀 주변의 평균값이나 분산을 고려해 지역별로 threshold를 정하므로, 그림자나 불균일한 조명이 있는 영상에서도 객체와 배경을 안정적으로 구분할 수 있다.

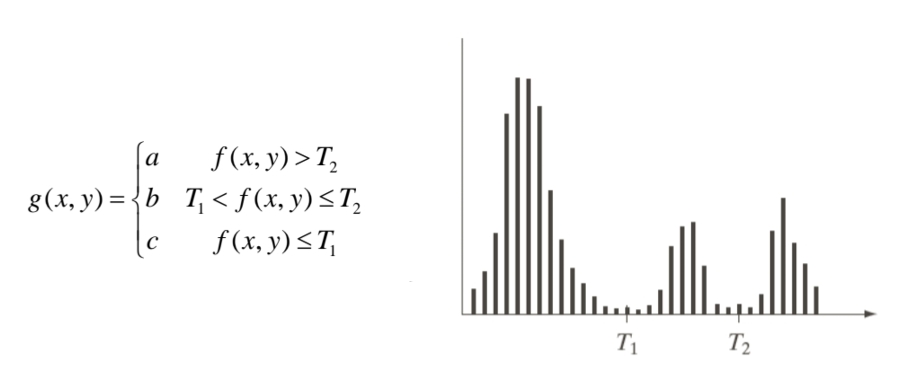
셋째, Multiple Thresholding(다중 임계값)은 하나의 임계값이 아니라 여러 개의 임계값을 설정해 픽셀 값을 여러 구간으로 나누는 방식이다. 예를 들어, $T_1, T_2$라는 두 개의 임계값이 있다면, $f(x,y) \le T_1$인 영역은 배경, $T_1 < f(x,y) \le T_2$인 영역은 객체1, $f(x,y) > T$인 영역은 객체2로 나눌 수 있다.

Thresholding은 구현이 간단하면서도 계산량이 적기 때문에 문서 영상의 이진화, 의료 영상에서 세포 영역 추출, 객체 검출의 전처리 단계 등에서 널리 활용된다. 다만 임계값의 선택에 따라 성능이 크게 달라지므로, 실제 응용에서는 전역적$\cdot$지역적 방법을 병행하거나, Otsu 방법과 같은 자동 임계값 결정 알고리즘이 사용되기도 한다.

Role of Noise in Image Thresholding

이미지 임계값 분할(Thresholding)에서 잡음의 역할
Thresholding은 영상의 밝기 분포를 기준으로 객체와 배경을 구분하는 기법이다. 그러나 실제 영상에는 다양한 잡음이 존재하고, 이 잡음은 히스토그램 분포를 흐리게 하여 임계값 결정에 큰 영향을 미친다.

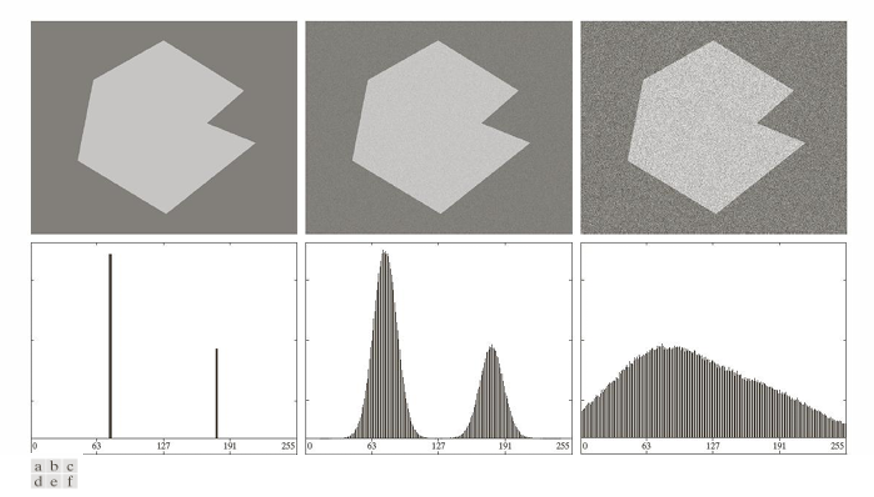
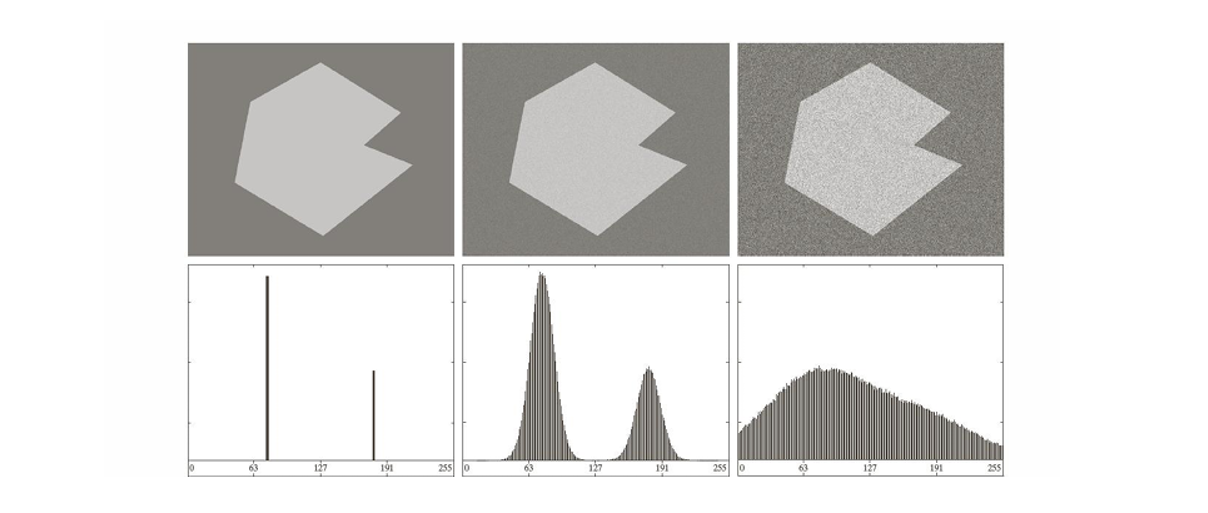
(a) Noiseless Image : 첫 번째 영상은 잡음이 없는 8비트 영상이다.

객체와 배경의 밝기가 명확히 다르므로, 히스토그램은 두 개의 뚜렷한 봉우리를 가진다. 이 경우, 두 피크 사이에 임계값을 설정하면 객체와 배경을 손쉽게 분리할 수 있다.

(b) Image with Low Gaussian Noise : 두 번째 영상은 평균 0, 표준 편차가 작은 ($\sigma = 10$ 정도) 가우시안 잡음이 추가된 경우이다.

잡음이 추가되면서 히스토그램의 두 봉우리가 퍼지지만, 여전히 분리된 상태를 유지한다. 따라서 임계값을 선택하기는 가증하지만, 경계 부분에서는 일부 픽셀이 잘못 분류될 수 있다.

(c) Image with High Gaussian Noise : 세 번째 영상은 표준편차가 큰($\sigma = 50$) 가우시안 잡음이 추가된 경우이다.

잡음이 강하게 섞이면서 객체와 배경의 밝기 차이가 거의 희석된다. 히스토그램은 두 봉우리의 경계가 사라지고 하나의 넓은 분포로 합쳐진다.

정리하면, 잡음이 없을 때는 히스토그램에서 뚜렷한 두 개의 봉우리가 형성되어 Thresholding이 용이하다.

잡음이 적을 때는 히스토그램이 퍼지지만 여전히 봉우리가 유지되어 Thresholding이 가능하지만 오류가 발생할 수 있다.

잡음이 심할 때는 히스토그램이 한 덩어리로 합쳐져, Thresholding이 거의 불가능해진다.

따라서 실제 응용에서는 잡음 제거를 위한 전처리(예: Smoothing, Gaussian Blur)나, 단일 임계값 대신 Adaptive Thresholding, Otsu 방법같은 더 정교한 접근이 필요하다.

Role of Illumination and Reflectance

조명과 반사율이 Thresholding에 미치는 영향
영상에서 각 픽셀의 밝기 값은 단순히 물체의 색(반사율, Reflectance)만으로 결정되지 않는다. 실제 값은 조명(Illumination)과 반사율의 곱으로 표현된다. 즉,

• $f(x, y)$ : 관측된 픽셀 밝기
• $i(x,y)$ : 조명(Intensity of illumination)
• $r(x,y)$ : 반사율(Reflectance of the object)

따라서 영상 분할을 단순히 밝기값 기준으로 수행하면, 조명 변화에 따라 같은 객체가 다르게 분류될 위험이 있다.

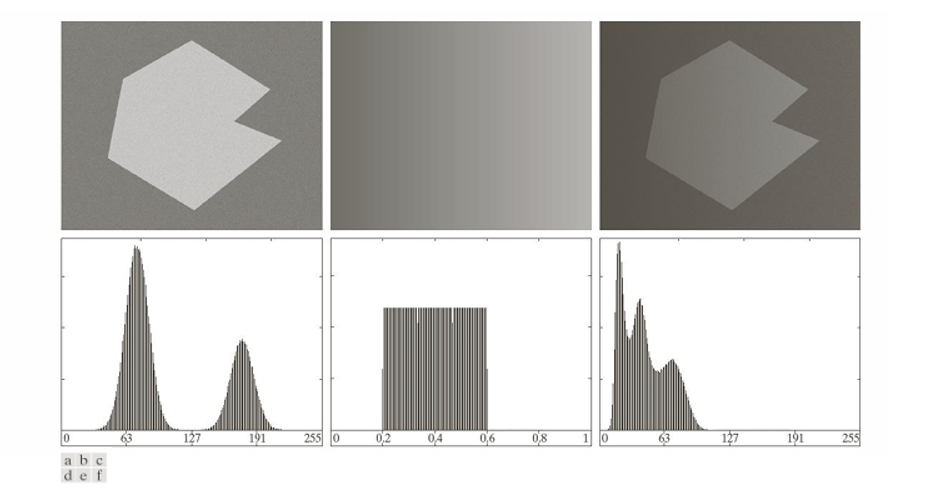
(a) Noisy Image : 첫 번째 영상은 잡음이 추가된 단순 객체 이미지이다.

히스토그램에는 두 개의 뚜렷한 봉우리가 존재하여, 객체와 배경을 비교적 쉽게 구분할 수 있다.

(b) Illumination Rammp : 두 번째 영상은 0.2~0.6 범위에서 선형적으로 변화하는 조명 분포(illumination ramp)이다.

이 영상은 조명이 위치에 따라 점진적으로 달라지는 상황을 모델링한다. 히스토그램은 균일한 분포를 가지며, Thresholding에는 별 의미가 없다.

(c) Product of Reflectanve x Illumination : 세 번째 영상은 (a)의 반사율 영상과 (b)의 조명 영상을 곱한 결과이다.

결과적으로 같은 객체임에도 불구하고, 조명 때문에 객체 내부의 픽셀 값이 넓은 범위에 걸쳐 분포하게 된다.

히스토그램에서는 원래 두 개의 뚜렷한 봉우리가 사라지고, 객체와 배경이 섞인 불명확한 분포가 나타난다.

즉, 이상적 상황(균일 조명)에서는 객체와 배경의 밝기 차이가 분명하겨 Thresholding이 효과적이다. 하지만 비균일 조명에서는 같은 객체라도 픽셀 값이 달렺, 하나의 임계값으로는 안정적인 분할이 불가능하다.

조명과 반사율의 상호작용은 영상의 픽셀 값을 크게 좌우한다. 따라서 Thresholding은 단순히 픽셀 밝기에 의존하기 때문에 조명 조건에 매우 민감하다. 이는 영상 분할의 근본적 한계 중 하나이며, 더 견고한 알고리즘에서는 조명 보정이나 고급 기법(예: Histogram Equalization, Retinex, Adaptive methods)을 사용하여 이를 극복한다.

Basic Global Thresholding

영상 분할에서 전역 임계값(Global Thresholding)은 영상 전체에 하나의 임계값 $T$를 적용하여 객체와 배경을 구분하는 방식이다. 그러나 단순히 임의의 $T$를 정하는 것이 아니라, 반복적(iterative) 방식으로 최적의 임계값을 점진적으로 찾아가는 방법이 많이 사용된다.

절차는 아래와 같다.

1. 초기 임계값 설정

• 임의의 초기 추정값 $T$를 선택한다.
• 일반적으로 영상의 평균 밝기값을 초기값으로 사용한다.

2. 영상 분할

• 임계값 $T$를 이용해 영상을 두 개의 영역으로 나눈다.
  • $G_1: f(x,y) > T$인 픽셀 집합(객체 후보)
  • $G_2: f(x,y) \le T$인 픽셀 집합(배경 후보)

3. 평균값 계산

• 각 영역의 평균 밝기값을 계산한다.
  • $m_1$ : 객체 후보 영역 $G_1$의 평균
  • $m_2$ : 배경 후보 영역 $G_2$의 평균

4. 새로운 임계값 갱신

• 새로운 임계값을 다음과 같이 계산한다.
  $T_{\text{new}} = \frac{m_1 + m_2}{2}$

5. 수렴 조건 확인

• $T$ 값이 이전 단계와 충분히 가까워질 때까지(즉, 변화량이 미리 정의한 작은 값보다 작아질 때까지) 2~4 단계를 반복한다.

아래는 Global Thresholding 예시 이미지이다.

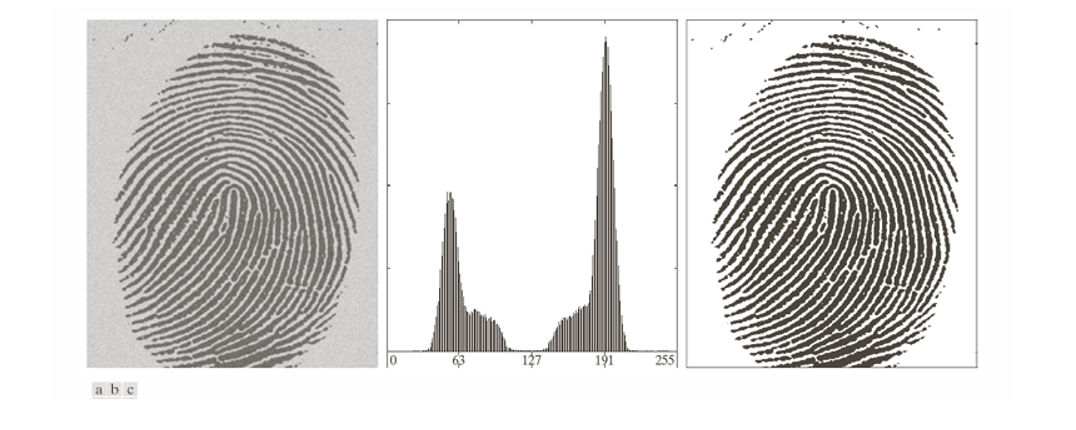
(a) 원본 영상 : 왼쪽 영상은 잡음이 포함된 지문 이미지이다. 영상 자체에 조명 불균일성과 잡음이 포함되어 있어, 단순분리에는 어려움이 있을 수 있다.

(b) 히스토그램 분석 : 중앙 그래프는 지문 영상의 히스토그램이다. 두 개의 주요한 peak가 나타난다. 이때 이 두 봉우리 사이 골(valley)이 임계값 $T$의 후보가 된다.

(c) Global Thresholding 결과 : 오른쪽 영상은 전역 임계값을 적용한 결과이다.

하나의 임계값 $T$를 기준으로 지문 능선과 배경이 효과적으로 분리되었다. 불필요한 잡음은 일부 남아 있지만, 전반적으로 지문의 구조를 뚜렷하게 추출할 수 있다.

Global Thresholding은 계산이 간단하면서도, 지문처럼 객체와 배경의 대비가 명확한 영상에서 효과적이다.

하지만, 조명 불균일, 잡음이 심한 경우에는 임계값 하나로는 적절한 분리가 어렵다. 이 경우 Adaptive Thresholding 같은 보완 기법이 필요하다.

Otsu's Method

Threshodling에서 가장 중요한 문제 중 하나는 "어떤 임계값 $T$를 선택할 것인가"이다. Otsu의 방법은 이 문제를 자동으로 해결하기 위해 제안된 알고리즘으로, 히스토그램 기반 접근을 사용한다.

핵심 아이디어
Otsu의 방법은 클래스 간 분산(between-class variance)을 최대화하는 임계값을 찾는 것이다.

히스토그램을 임계값 $k$를 기준으로 두 클래스(배경, 객체)로 나눈다. 클래스 간 분산이 크다는 것은 곧 두 그룹이 평균적으로 멀리 떨어져 있어, 더 잘 분리된다는 의미이다.

수식
클래스 간 분산은 다음과 같이 정의된다.

• $P_1$ : 임계값 $k$에서 클래스 1(예: 배경)의 확률
• $P_2$ : 임계값 $k$에서 클래스 2(예: 객체)의 확률
• $m_1$ : 클래스 1의 평균
• $m_2$ : 클래스 2의 평균
• $m_G$ : 영상 전체(global)의 평균

즉, 각 클래스 평균과 전체 평균의 차이를 확률로 가중해 합한 값이다.

알고리즘 절차
1. 영상 히스토그램을 구한다.
2. 가능한 모든 임계값 $k$에 대해 클래스 간 분산 $\sigma_B^2$를 계산한다.
3. $\sigma_B^2$가 최대가 되는 $k$를 최적의 임계값으로 선택한다.

Otsu's Method의 장단점

장점
임계값을 자동으로 찾을 수 있어 사람이 직접 설정할 필요가 없다. 영상 히스토그램이 쌍봉 형태(bimodal)일 때 매우 효과적이다.

단점
객체와 배경의 히스토그램이 많이 겹치거나, 다중 객체가 존재하는 경우에는 성능이 떨어진다. 잡읍과 조명 변화에도 민감하다.

정리하자면,
Otsu의 방법은 히스토그램을 기반으로 두 클래스(객체와 배경)를 가장 잘 분리하는 임계값을 선택하는 자동화 기법이다. “클래스 간 분산이 최대가 되는 임계값 = 최적의 임계값”이라는 원리를 따른다.

(a) 원본 영상 : 배경과 객체의 밝기 차이가 존재하지만, 전역적으로 명확히 분리되지 않는다. 조명 불균일성 및 다양한 밝기 수준 때문에 Thresholding이 쉽지 않은 상황이다.

(b) 히스토그램 : 특정 밝기 구간에 픽셀이 집중되어 있으며, 여러 봉우리가 혼합된 형태를 보인다. 이 경우 단순히 하나의 임계값을 선택하면 객체와 배경이 명확히 분리되지 않을 수 있다.

(c) Global Thresholding 결과 : 왼쪽 하단은 기본 전역 임계값 알고리즘으로 분할한 결과이다.

하나의 임계값만 적용했기 때문에, 배경 일부가 객체로 잘못 분류되거나 객체의 일부가 배경으로 날아가 버린다. 즉, 객체와 배경의 경계가 불명확하고 오류가 많다.

(d) Otsu's Method 결과 : 오른쪽 하단은 Otsu의 방법으로 자동 임계값을 선택해 분할한 결과이다.

히스토그램의 분산을 고려하여 최적의 임계값을 선택했기 때문에, 객체(원형 구조물)와 배경이 더 잘 구분되다.

결과적으로 객체의 형태가 보존되고, 배경 노이즈도 줄어든 것을 확인할 수 있다.

정리하면, Global Thresholding은 단순하고 빠르지만, 히스토그램 분포가 복잡하거나 조명이 불균일한 경우 정확도가 떨어진다. Otsu's Method는 자동으로 임계값을 결정하고, 클래스 간 분산을 최대화하므로 더 안정적인 결과를 제공한다.

Using Edges to Improve Global Thresholding

에지를 활용한 전역 임계값 개선
전역 임계값은 영상 전체의 히스토그램을 기반으로 객체와 배경을 분리한다. 하지만 객체가 작고 배경이 넓은 경우, 히스토그램은 배경에 해당하는 큰 봉우리(peak)에 의해 지배된다.

이때 작은 객체의 분포는 히스토그램에서 거의 묻혀버려, 적절한 임계값을 찾기 어렵다. 결과적으로 작은 객체는 배경에 합쳐지거나 제대로 검출되지 않는 문제가 발생한다.

개선 방법: 에지 기반 접근
이를 해결하기 위한 한 가지 방법은, 영상 전체 픽셀이 아니라 객체와 배경의 경계(edge) 부근 픽셀만 고려하여 히스토그램을 구성하는 것이다.

객체와 배경을 구분하는 핵심 정보는 경계 부근에 존재한다. 따라서 에지 근처 픽셀만을 대상으로 히스토그램을 만들면, 객체와 배경을 더 명학히 구분할 수 있다. 이렇게 하면 히스토그램에서 두 클래스(객체, 배경)의 분포가 더욱 뚜렷해져, 전역 임계값 선택이 개선된다.

Otsu 방법의 한계: 잡음이 심한 경우

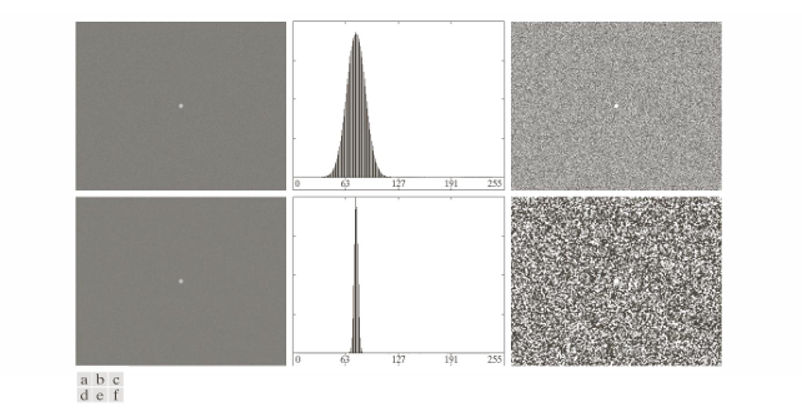
(a) 원본 영상(Noisy Image) : 좌측 상단 영상은 매우 작은 객체(하얀 점)가 있고, 배경 전반에 잡음이 섞여 있는 영상이다.

(b) 히스토그램을 보면, 하나의 봉우리에 대해 대부분의 픽셀이 집중되어 있다.

작은 객체의 픽셀은 전체 픽셀 수에 비해 너무 적어서, 히스토그램에 거의 영향을 주지 못한다. 따라서 배경 분포만 크게 보이고, 객체의 정보는 묻혀 버린다.

(c) Otsu 방법 결과 : Otsu 알고리즘을 적용했지만, 객체와 배경이 명확히 분리되지 않았다. 이유는 Otsu는 클래스 간 분산을 최대화하는 임계값을 찾는데, 여기서는 작은 객체가 전체 통계량에 기여하지 못해 올바른 분할이 불가능하다.

(d) 스무딩 적용 영상 : 좌측 하단은 잡음을 줄이기 위해 $5\times 5$ 평균 필터를 적용한 영상이다. 배경 잡음은 다소 줄었지만, 여전히 객체의 비율이 너무 작다.

(e) 스무딩 후 히스토그램 : 히스토그램은 더 날카로운 하나의 봉우리로 변했지만, 여전히 객체의 픽셀은 통계적으로 무시된다.

(f) Otsu 방법 결과 : 스무딩 후 다시 Otsu를 적용했지만, 결과적으로 객체 검출에 실패했다. 히스토그램이 여전히 단일 봉우리(unimodal)에 가까워, 두 클래스를 구분할 수 없기 때문이다.

Otsu 방법 개선: 에지 기반 접근

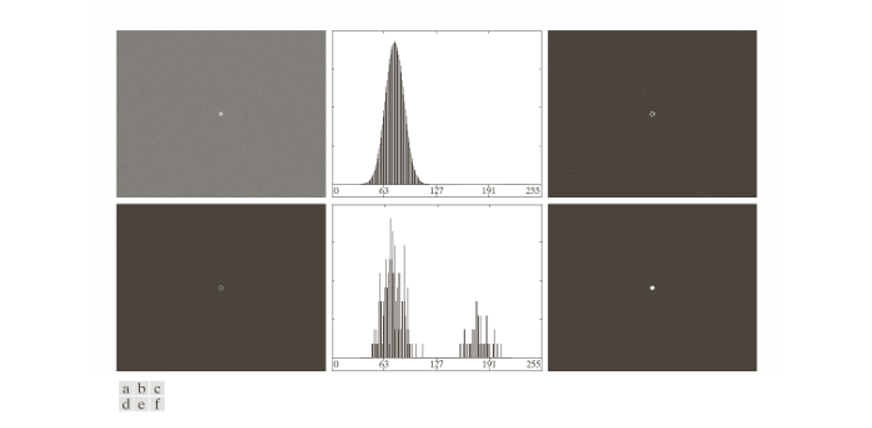
(a) 원본 영상 : 왼쪽 상단은 이전 예시와 동일한 잡음이 많은 영상으로 작은 객체가 배경 속에 묻혀 있다.

(b) 히스토그램 : 오른쪽 상단은 영상 전체 픽셀의 히스토그램이다.

배경 픽셀이 대부분을 차지하므로 단일 봉우리 형태를 보인다. 이 상태에서는 Otsu 방법이 객체를 검출하기 어렵다.

(c) Gradient Magnitude Thresholding : 우측 상단 영상은 경계(Gradient magnitude)를 이용해 픽셀을 강조한 결과이다.

잡음이 대부분은 제거되고, 객체 주변의 경계 부분이 남는다. 특히 상위 99.7%의 강한 gradient만 남겨, 객체와 배경의 차이를 부각시켰다.

(d) 결합 영상(a x c) : 왼쪽 하단은 원본 영상(a)과 gradient 영상(c)를 곱한 결과이다.

잡음이 줄고, 객체 영역이 상대적으로 더 뚜렷해진다. 즉, 원본 영상에서 객체와 관련성이 높은 픽셀만 강조된 것이다.

(e) 새로운 히스토그램 : 오른쪽 하단 그래프는 (d) 영상의 픽셀들로 구성한 히스토그램이다.

이전과 달리, 두 개의 봉우리(객체 vs 배경)가 뚜렷하게 분리된다. 이제 Otsu 방법을 적용할 수 있는 조건이 갖춰진다.

(f) 최종 분할 결과 : 왼쪽 하단 영상은 (e)의 히스토그램을 기반으로 Otsu 방법을 적용한 결과이다.

임계값은 약 124로 선택되었고, 이는 두 봉우리 사이의 중간값에 해당한다.

결과적으로 작은 객체가 잡음 배경 속에서 성공적으로 분리되었다.

단순한 Otsu 방법은 배경 잡음에 묻힌 작은 객체를 분리하지 못한다. 그러나 gradient 기반 전처리를 적용하면, 객체와 배경의 경계가 강조되어 히스토그램이 개선된다. 그 후 Otsu를 적용하면 안정적인 분할 결과를 얻을 수 있다.

Otsu vs Edge-based Preprocessing

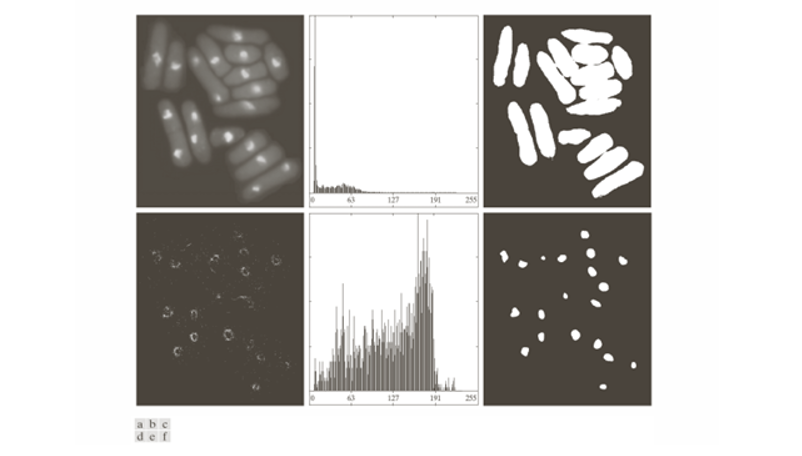
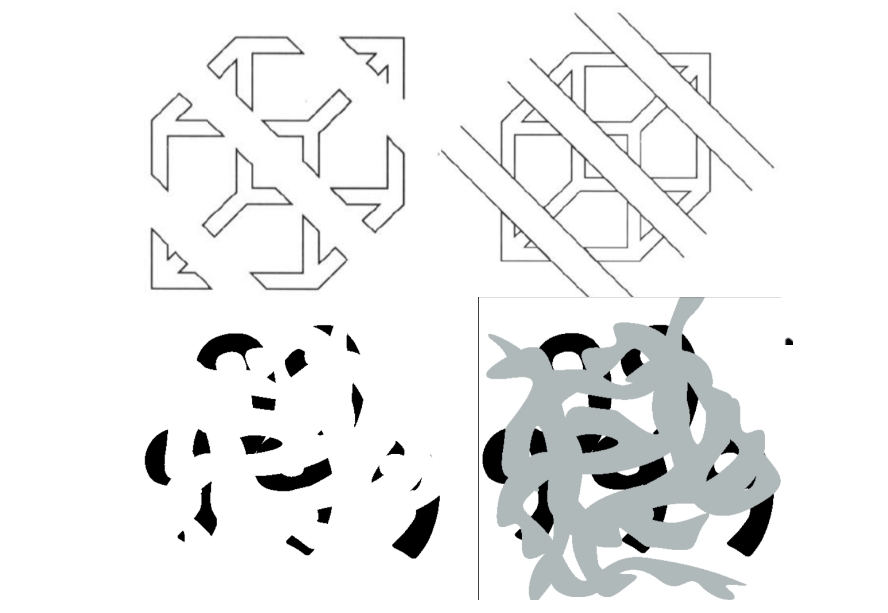
(a) 원본 영상 : 왼쪽 상단은 현미경으로 촬영한 효모 세포 이미지이다.

세포와 배경의 명암 대비가 크지 않아서, 단순 임계값만으로는 정확한 분할이 어렵다. 세포 주변이 흐릿하게 번져 있어서 히스토그램도 불분명하다.

(b) 히스토그램 : 가운데 상단은 원본 영상의 히스토그램이다.

배경 픽셀이 대부분을 차지해 하나의 큰 봉우리가 형성되었다. 세포 영역을 반영하는 작은 분포는 묻혀 있어서, 전역 임계값으로는 좋은 분할이 기대되기 어렵다.

(c) Otsu 방법 결과 : 오른쪽 상단 (b)는 히스토그르ㅐㅁ을 기반으로 Otsu 방법을 적용한 결과이다.

큰 세포 덩어리는 어느 정도 검출되었지만, 작은 세포들이 배경과 섞여 제대로 구분되지 않았다. 즉, 세포와 배경의 분리가 불완전하다.

(d) Absolute Laplacian : 왼쪽 하단은 원본 영상에 라플라시안(Laplacian) 필터를 적용한 뒤 절댓값을 취한 영상이다.

라플라시안은 영상의 2차 미분 연산자로, 밝기 변화가 큰 경계(Edge)를 강조한다. 그 결과 세포의 외곽선 부분이 두드러지게 나타난다.

(e) 새로운 히스토그램 : 가운데 하단은 (a)와 (d)를 곱해 만든 영상에서 픽셀들을 대상으로 얻은 히스토그램이다.

이번에는 세포와 배경의 픽셀이 보다 명확히 구분되어 두 개의 봉우리가 형성된다. 따라서 임계값을 적용하기에 훨씬 좋은 조건이 된다.

(f) 개선된 Otsu 결과 : 오른쪽 하단은 (e)의 히스토그램을 기반으로 Otsu 방법을 다시 적용한 결과이다.

세포들이 독립적으로 잘 분리되어 검출되었다. 전처리를 하지 않은 (c) 결과와 비교하면 훨씬 깔끔하게 객체(세포)와 배경이 구분된다.

아래 예시의 기본 절차는 위 예시와 동일하다. 차이점은, 라플라시안 절대값 영상의 임계값을 더 낮게 선택하였다.

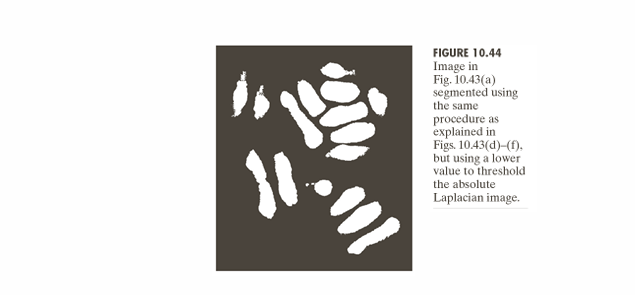
결과적으로, 낮은 임계값을 사용했기 때문에, 더 많은 에지 픽셀이 살아남았다. 이로 인해 세포 영역이 조금 더 넓게 검출되었다.

높은 임계값일 때는 라플라시안 영상에서 아주 강한 경계(edge)만 통과시킨다. 결과적으로 위 예시에서 객체 전체가 아니라 세포 내부의 핵 부분만 검출됨을 확인할 수 있다.

낮은 임계값일 떄는 라플라시안 영상에서 약한 에지까지 포함한다. 세포 외곽이나 세포질 부분처럼, 비교적 완만한 경계도 남기 때문에 세포 전체가 하나의 덩어리로 잡힌다. 결과적으로 세포 전체 영역이 분리되어 더 잘보인다.

Multiple Thresholds

다중 임계값 분할
일반적으로 Otsu 방법은 히스토그램을 두 부분(배경, 객체)으로 나누어 클래스 간 분산($\sigma^2_B$)이 최대가 되는 임계값을 찾는다.

하지만 영상에는 객체가 하나만 있는 게 아니라, 여러 개의 구분되는 영역(예: 배경 + 객체1 + 객체2...)이 있을 수 있다.

이 경우 임계값을 여러 개 설정하여 픽셀을 K개의 클래스로 나눈다.

다중 임계값에서 클래스 간 분산은 다음과 같이 일반화된다.

• $P_k$ : 클래스 $k$에 속하는 픽셀의 확률(히스토그램 비율)
• $m_k$ : 클래스 $k$의 평균 밝기값
• $m_G$ : 전체 영상의 전역 평균

즉, 각 클래스의 평균과 전체 평균의 차이를, 그 클래스의 확률로 가중합한 값이다. 이 값이 최대가 되도록 임계값들을 선택한다.

예시

• 이진 분할(Binary Thresholding) : 임계값 1개, 클래스 2개(객체 vs 배경)
• 삼분할(Triple Thresholding) : 임계값 2개, 클래스 3개(예: 어두운 영역, 중간 영역, 밝은 영역)
• 다중 분할(K-thresholding) : 임계값 K-1개, 클래스 K개

예를 들어, CT 영상에서, 뼈(밝은 영역), 근육(중간 밝기), 공기/배경(어두운 영역)을 구분할 때 다중 임계값이 필요하다.

Multiple Thresholds는 객체가 둘 이상일 때 유용하며, Otsu의 방법을 확장했기 때문에, 여전히 자동화된 방식으로 임계값을 찾을 수 있다.

하지만, 클래스 수(K)를 미리 알아야하며, K가 커질수록 계산량이 증가한다. 또한 히스토그램이 뚜렷하게 구분되지 않는 경우 성능이 저하될 수 있다.

즉, Multiple Thresholds는 Otsu 방법을 확장해, 영상을 여러 영역으로 나누는 기법이다. 클래스 수가 많을수록 더 정교한 분할이 가능하지만, 계산량과 잡음 민감성이 커진다는 점을 고려해야 한다.