[CV] Motion(1) - Optical Flow

Yeontachi·2025년 8월 27일

Computer Vision Note

목록 보기

44/47

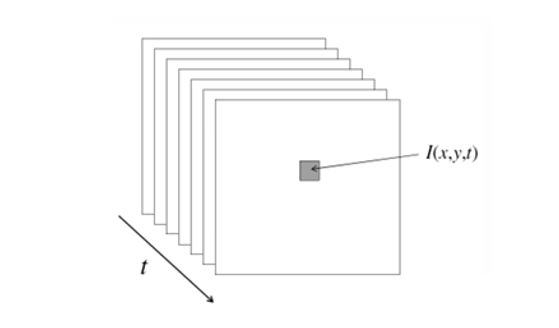
비디어(Video)는 시간에 따라 연속적으로 촬영된 프레임들의 집합이다. 따라서 정적인 이미지가 단순히 공간 좌표 $(x,y)$ 에 의존하는 함수라면, 비디오는 시간 축(t)이 추가된 함수 $I(x,y,t)$ 로 표현된다. 이로 인해 우리는 픽셀의 위치뿐만 아니라, 시간이 흐르면서픽셀이 어떻게 변화하는지를 분석할 수 있다.

Motion의 활용
컴퓨터 비전에서 움직임(Motion)은 매우 중요한 단서를 제공한다.

3D 구조 복원(Structure Reconstruction): 여러 프레임에서 얻은 움직임 단서를 활용해 장면의 3차원 구조를 추정한다.
객체 분할(Object Segmentation from Motion): 같은 움직임을 공유하는 픽셀들을 모아 객체 단위로 분할한다.
동적 모델 추적(Dynamical Models Tracking): 물체의 운동 궤적을 학습하고 추적한다.
이벤트 및 활동 인식(Event & Activity Recognition): 사람의 동작이나 장면 내 사건을 인식한다.
비디오 품질 향상(Video Quality Improvement): 흔들림 보정, 노이즈 제거 등 영상 후처리에 활용된다

Motion Field
실세계에서 3차원 물체가 움직이면, 카메라 영상 평면에 그 움직임이 투영(Projection)된다. 이를 Motion Field라 하며, 실제 물체의 움직임과 영상 속에서 관측되는 겉보기 이동(apparent motion)의 관계를 설명한다. 예를 들어, 루빅스 큐브가 회전하는 경우, 실제 3D 운동은 복잡하지만 이미지 평면에서는 2D 화살표 벡터의 집합으로 나타난다.

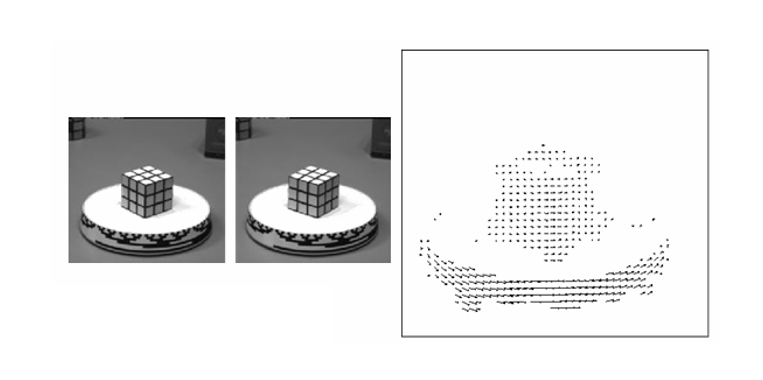
즉, Motion Field는 실제 장면의 3D 운동 $\to$ 영상의 2D 좌표 변화로 이어지는 변환 결과이며, Optical Flow는 이를 근사적으로 추정하는 과정이라고 할 수 있다.

Optical Flow

Optical Flow는 영상에서 밝기 패턴(brightness pattern)의 겉보기 움직임(apparent motion)을 의미한다. 중요한 점은 이것이 실제 물체의 3차원 운동과 항상 일치하지는 않는다는 것이다.

예를 들어, 구가 회전할 때 또는 조명이 움직일 때도 영상의 밝기 패턴이 변하여 Optical Flow가 발생할 수 있다. 즉, Optical Flow는 실제 물체 운동과 조명 조건 모두의 영향을 받는다.

Optical Flow는 시간에 따른 영상의 밝기 변화량을 벡터장(vector field)으로 표현한다.

위 그림처럼, 장면 속 각 픽셀마다 "어느 방향으로, 얼마나 이동했는가"를 나타내는 벡터가 주어진다. 따라서 Optical Flow는 공간적-시간적 영상 변화의 집합을 시각적으로 직관화한 결과라 할 수 있다.

Optical Flow 추정(Estimating Optical Flow)

두 연속된 프레임 $I(x,y,t-1)$ 과 $I(x,y,t)$ 가 주어졌을 때, 픽셀 단위의 이동 $(u(x,y), v(x,y))$ 를 추정하는 것이 Optical Flow 계산이다.

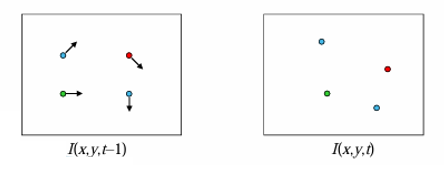
이를 위해 세 가지 주요 가정을 둔다.

밝기 보존 가정(Brightness Constancy)
동일한 물체 점은 시간이 지나도 같은 밝기를 유지한다.
$I(x,y,t) = I(x+u, y+v, t+1)$
작은 이동 가정(Small Motion)
프레임 간 이동은 충분히 작아 선형 근사(Taylor expansion)가 가능하다.
공간적 일관성 가정(Spatial Coherence)
인접한 픽셀들은 비슷한 움직임을 가진다. 이는 지역적 윈도우 기반 추정(Lucas-Kanade 등)에 활용된다.

Color/Brigtness Constancy

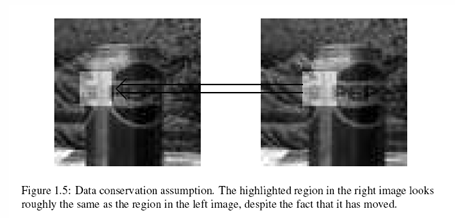
연속된 두 프레임에서, 같은 물체 점은 밝기를 유지한다고 가정한다.

I(x,y,t-1) = I(x+u, y+v, t)

$I(x,y,t)$ : 위치 $(x,y)$ , 시간 $t$ 에서의 픽셀 밝기
$(uv)$ : 픽셀의 변위(displacement), 즉 Optical Flow 벡터

위 식의 오른쪽 항을 테일러 전개하면,

I(x+u, y+v, t) \approx I(x,y,t) + I_x u + I_y v

따라서,

I(x,y,t-1) \approx I(x,y,t) + I_x u + I_y v

이를 시간 변화량 $I_t = I(x,y,t) - I(x,y,t-1)$ 를 포함시켜 정리하면:

I_x u + I_y v + I_t \approx 0

최종적으로 Optical Flow Constraint Equation은 다음과 같다.

I_x u + I_y v + I_t = 0

또는 기울기 벡터 표현으로:

\nabla I \cdot (u,v) + I_t = 0

$I_x, I_y$ : 영상의 공간적 기울기 (x, y 방향 밝기 변화율)
$I_t$ : 영상의 시간적 기울기 (밝기 변화율)
$(u,v)$ : 우리가 구하고자 하는 Optical Flow 벡터

문제점 Aperture Problem(수정 필요)

Optical Flow를 계산할 때, 한 점의 밝기 변화만으로는 실제 운동을 고유하게 결정할 수 없다.

즉, 한 픽셀에서 얻는 방정식은 하나지만, 미지수는 두 개($u,v)이므로 해가 무수히 많다. 이를 Aperture Problem(개구 문제)라고 부른다.

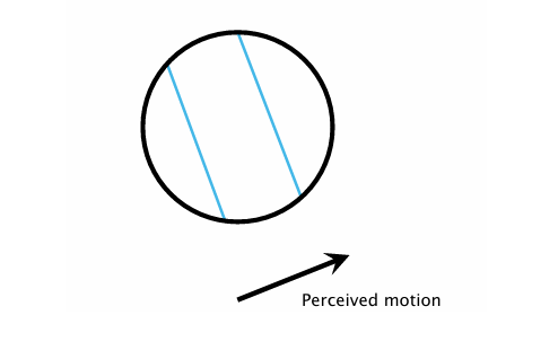
위 그림을 보면, 원형 창(개구, aperture)을 통해 사선(에지)을 관찰할 때,에지 방향 ↘의 수직한 방향 성분인 ↗방향으로 보인다.

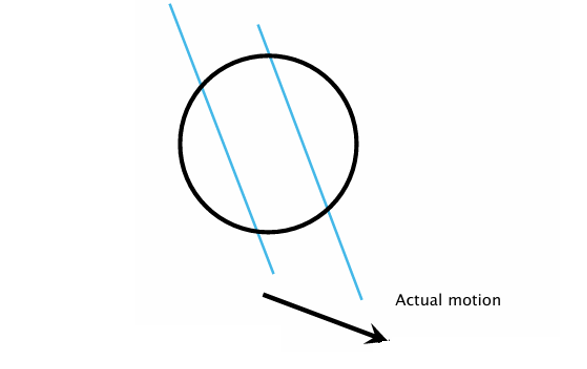
실제로 선분이 대각선 방향(↘)으로 이동하고 있지만, 개구 안에서 보이는 정보만으로는 이 전체 움직임을 알 수 없다. 결국, 우리가 인지하는 Optical Flow는 실제 움직임의 일부(법선 방향)만 반영한다.

직관적인 예시로, Barber Pole Illusion(이발소 막대 착시)를 들 수 있다. 아래 이미지처럼 원형 창 안에서 보면 사람 눈에는 줄무늬가 (↘) 방향으로 움직이는 것처럼 보인다.

하지만 실제 사선 줄무늬는 (↓) 방향으로 움직이고 있다.

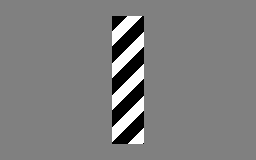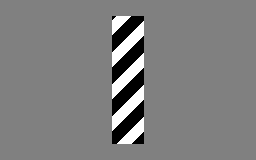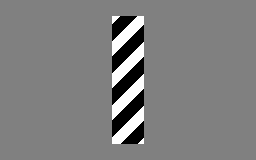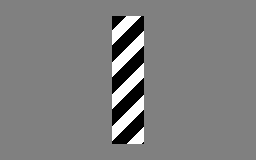
Aperture Problem 해결 방법

1. 아이디어: 더 많은 방정식 만들기

한 픽셀에서는 식이 1개, 미지수는 2개( $u,v$ ) → 해를 고유하게 못 구함.
해결책: 주변 픽셀들이 같은 움직임( $u,v$ )을 가진다고 가정한다.
- 예: $5 \times 5$ 윈도우를 쓰면 25개의 픽셀 → 25개의 식 생성

즉, 하나의 픽셀만 보지 않고 **작은 지역(window)**을 묶어서 같이 푼다.

2. 행렬 표현

25개의 식을 모으면 다음과 같은 선형 시스템이 된다:

A \cdot d = b

여기서

$A = \begin{bmatrix} I_x(p_1) & I_y(p_1) \\ I_x(p_2) & I_y(p_2) \\ \vdots & \vdots \\ I_x(p_{25}) & I_y(p_{25}) \end{bmatrix}_{25 \times 2}$
$d = \begin{bmatrix} u \\ v \end{bmatrix}_{2 \times 1}$
$b = -\begin{bmatrix} I_t(p_1) \\ I_t(p_2) \\ \vdots \\ I_t(p_{25}) \end{bmatrix}_{25 \times 1}$

3. 최소자승법 (Least Squares Solution)

방정식이 많으므로(25식 vs 2미지수), 최소자승해를 구한다.

\min_d \|A d - b\|^2

이를 풀면:

(A^T A) d = A^T b

즉,

\begin{bmatrix} \sum I_x^2 & \sum I_x I_y \\ \sum I_x I_y & \sum I_y^2 \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} = - \begin{bmatrix} \sum I_x I_t \\ \sum I_y I_t \end{bmatrix}

4. 해가 존재하려면? (조건)

이 시스템이 풀리려면:

$A^T A$ 가 역행렬 가능해야 함 (invertible)
- 즉, 두 방향으로 충분한 기울기 정보가 있어야 한다.
고유값 $\lambda_1, \lambda_2$ 가 너무 작지 않아야 함
- 작으면 flat 영역이라 흐름 추정이 불가하다.
조건수 $\lambda_1 / \lambda_2$ 가 너무 크지 않아야 함
- 너무 크면 한쪽 방향으로만 정보가 강해서 불안정해진다. (edge의 경우).

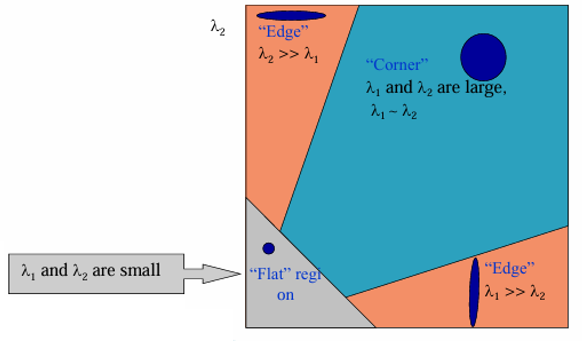
즉,

Flat 영역 (균일한 밝기): $\lambda_1, \lambda_2$ 둘 다 작음 → Optical Flow 불가능.
Edge 영역 (한 방향으로만 변화): 한 고유값만 큼 → Aperture Problem 여전.
Corner 영역 (두 방향으로 다 변화): 두 고유값 다 큼 → 안정적으로 Optical Flow 계산 가능.

Optical Flow, Gradient 분포에 따른 차이

Edge 영역
에지 영역은 건물의 지붕선이나 나무 기둥 경계처럼 한 방향으로만 밝기 변화가 강한 부분이다. 이 경우 영상 기울기는 매우 크지만, 특정 방향(즉, 에지 수직 방향)에만 정보가 집중된다. 수학적으로는 고유값 $\lambda_1$ 은 크지만 $\lambda_2$ 는 작다. 따라서 Optical Flow를 계산하면 흐름의 수직 성분은 안정적으로 구할 수 있지만, 평행 성분은 알 수 없어 해가 불완전하다. 이런 한계 때문에 에지 영역은 Aperture Problem을 피할 수 없다.

Low-texture 영역
균일한 벽이나 하늘처럼 밝기 변화가 거의 없는 부분은 기울기 크기가 전반적으로 매우 작다. 이 경우 두 고유값 $\lambda_1, \lambda_2$ 모두 작은 값을 가지며, Optical Flow를 추정할 수 있는 정보가 전혀 없다. 결국 이러한 영역에서는 어떤 방향으로 움직이는지 전혀 계산할 수 없으며, Optical Flow가 불가능하다.

High-texture 영역
나뭇잎이 무성한 부분이나 창문 모서리처럼 두 방향으로 모두 밝기 변화가 큰 부분은 기울기가 다양하게 분포되어 있다. 이때 두 고유값 $\lambda_1, \lambda_2$ 가 모두 크고 서로 비슷한 값을 가지게 된다. 이 영역은 두 방향 모두 충분한 정보를 제공하므로, Optical Flow를 안정적이고 신뢰성 있게 계산할 수 있다. 따라서 이런 영역은 흔히 Corner 영역이라고 부르며, 특징점 검출 및 추적에서 중요한 역할을 한다.

정리하면, Flat 영역은 정보가 없어 Optical Flow가 불가능하며, Edge 영역은 한쪽 방향 정보만 존재해 Aperture Problem이 발생한다. 반면, Corner/High-texture 영역은 두 방향 정보 모두 풍부해 Optical Flow를 안정적으로 계산이 가능하다.

결국 Optical Flow를 제대로 계산하기 위해서는 코너나 텍스처가 풍부한 영역을 선택하는 것이 중요하다. 이 때문에 Lucas-Kanade Optical Flow와 같은 알고리즘은 코너 특징점을 기반으로 움직임을 추적하며, Harris Corner Detector나 Shi-Tomasi Detector와 같은 코너 검출기가 함께 사용된다.