[CV] Segmentation(2) - K-Means Clustering

Yeontachi·2025년 8월 26일

Computer Vision Note

목록 보기

37/47

영상 분할(Segmentation)은 영상을 객체 단위로 나누는 중요한 과정이며, 클러스터링은 이를 실현하는 대표적인 방법 중 하나이다. 클러스터링은 픽셀들을 특징 공간(feature space)에 배치한 후, 유사한 속성을 가진 픽셀들을 묶어 영역을 형성하는 방식이다. 이 과정에서 많이 활용되는 방법이 K-means Clustering과 Mean Shift Clustering이다.

K-means Clustering은 사전에 클러스터 개수 $K$ 를 지정하고, 각 픽셀을 가장 가까운 중심에 할당하여 평균값으로 중심을 갱신하는 반복 알고리즘이다. 계산이 단순하고 빠르다는 장점이 있지만, $K$ 를 미리 알아야 하고 복잡한 구조나 비선형 분포에는 잘 맞지 않는다는 한계가 있다.

이에 비해 Mean Shift Clustering은 데이터의 분포(density) 자체를 기반으로 고밀도 영역을 찾아 클러스터를 형성하는 비모수(non-parametric) 방법이다. 즉, 클러스터 개수를 지정할 필요 없이, 데이터가 밀집한 영역을 모드(mode)로 삼아 픽셀들을 이동시키며 그룹화한다. 이 방식은 객체의 실제 경계를 잘 반영하고 다양한 스케일의 영역 분할이 가능하지만, 계산량이 크고 윈도우 크기(커널 대역폭)의 선택에 민감하다.

결과적으로, K-means는 빠르고 단순한 색상 기반 분할에 적합하며, Mean Shift는 더 정교하고 객체 중심적인 분할에 효과적이다. 두 방법 모두 영상 분할을 클러스터링 문제로 해석한 좋은 사례이며, 응용 목적과 데이터 특성에 따라 선택적으로 활용된다.

K-Means clustering

K-Means 알고리즘은 데이터를 K개의 그룹으로 나누어, 각 그룹 내의 데이터가 최대한 유사하도록 만드는 대표적인 클러스터링 방법이다. 이 과정은 반복적(iterative)으로 수행되며, 수렴할 때까지 클러스터 중심(centroid)을 갱신한다.

Step 1: 초기화

$K$ 개의 클러스터 중심 $c_1, c_2,...,c_k$ 를 무작위로 선택한다.
초기 중심 선택은 결과에 큰 영향을 미치기 때문에, 여러 번 실행하거나 K-means++ 같은 개선된 초기화 방법을 사용하기도 한다.

Step 2: 할당 단계(Assignment Step)

각 데이터 포인트 $p$ 에 대해, 가장 가까운 클러스터 중심 $c_i$ 를 찾는다.
거리 척도로는 일반적으로 유클리드 거리(Euclidean distance)를 사용한다.
$p$ 는 해당 클러스터 $i$ 에 속하게 된다.

Step 3: 갱신 단계(Update Step)

각 클러스터에 속한 모든 포인트들의 평균을 계산한다.
이 평균값이 새로운 클러스터 중심 $c_i$ 가 된다.

Step 4: 반복

클러스터 중심이 더 이상 변하지 않거나, 변화가 매우 작아질 때까지 Step2와 Step3을 반복한다.
보통 알고리즘은 몇 번의 반복 후 수렴한다.

K-means는 다음 목적 함수(cost function)을 최소화하는 알고리즘이다.

J = \sum_{k=1}^K\sum_{x_i \in C_k} ||x_i - μ_k||^2

$C_k$ : 클러스터 $k$ 에 속한 데이터 집합
$μ_k$ : 클러스터 $k$ 의 중심(평균값)
$x_i$ : 데이터 포인트

즉, 각 데이터가 속한 클러스터 중심까지의 거리 제곱합을 최소화하는 방향으로 클러스터를 형성한다.

K-means 알고리즘의 단계별 동작

1단계: 클러스터 개수 설정
사용자가 원하는 클러스터 개수 $K$ 를 지정한다.(예: $K = 5$ )

이 단계는 K-means의 가장 큰 제약 중 하나인데, 클러스터 수를 사전에 알아야 한다는 점이다.

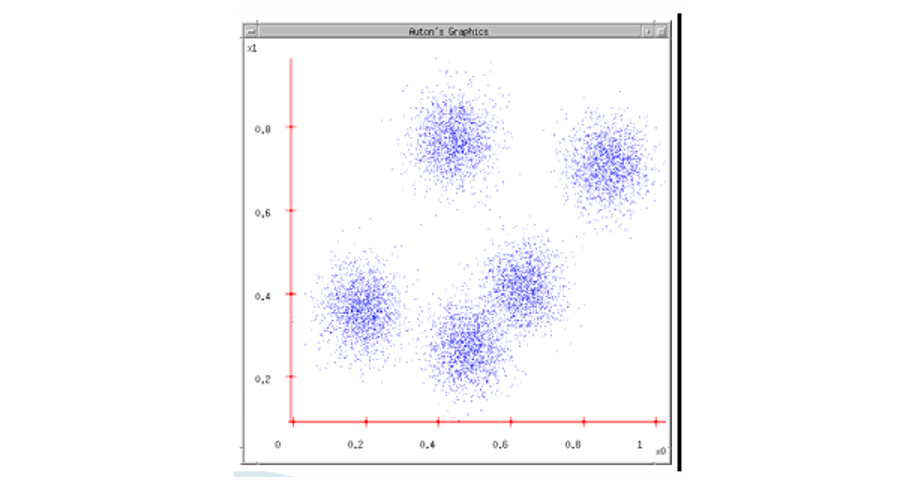
2단계: 초기 중심(centroid) 선택
무작위로 $K$ 개의 중심을 영상/데이터 공간 내에 배치한다.

초기 중심 위치에 따라 결과가 달라질 수 있어, K-means++ 같은 개선된 초기화 방법을 사용하기도 한다.

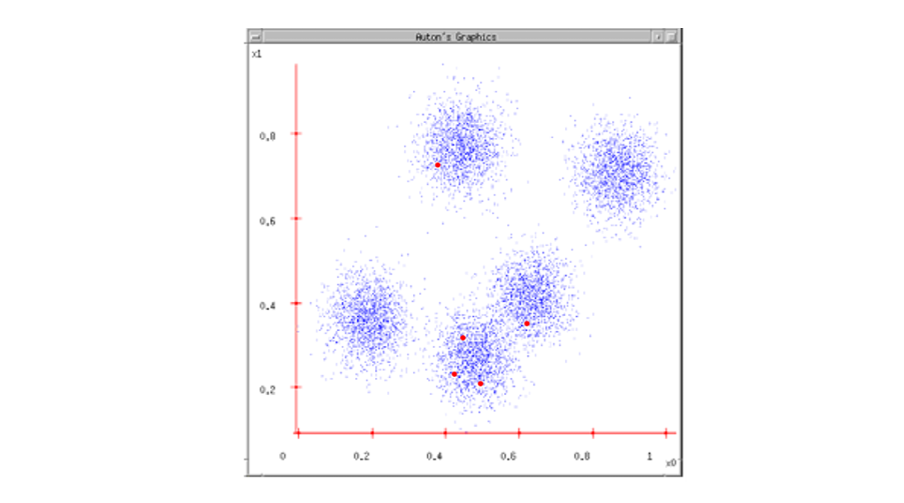
3단계: 할당(Assignment)
각 데이터 포인트(여기서는 파란 점)는 가장 가까운 중심점(빨간 점)에 할당된다.

결과적으로 데이터 공간이 Voroni Diagram 형태로 나뉜다.
즉, 각 중심점은 자기 "구역" 내에 있는 데이터를 소유하게 된다.

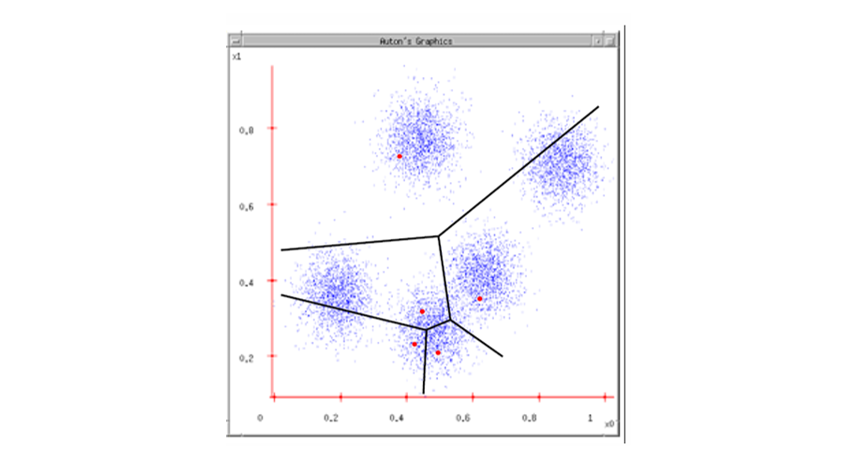
4단계: 중심 갱신(Update)
각 클러스터에 속한 데이터들의 평균값을 계산하고, 그 값을 새로운 중심점으로 갱신한다.

그림에서 빨간 점이 초록 점으로 이동하는 모습이 이 과정을 잘 보여준다.

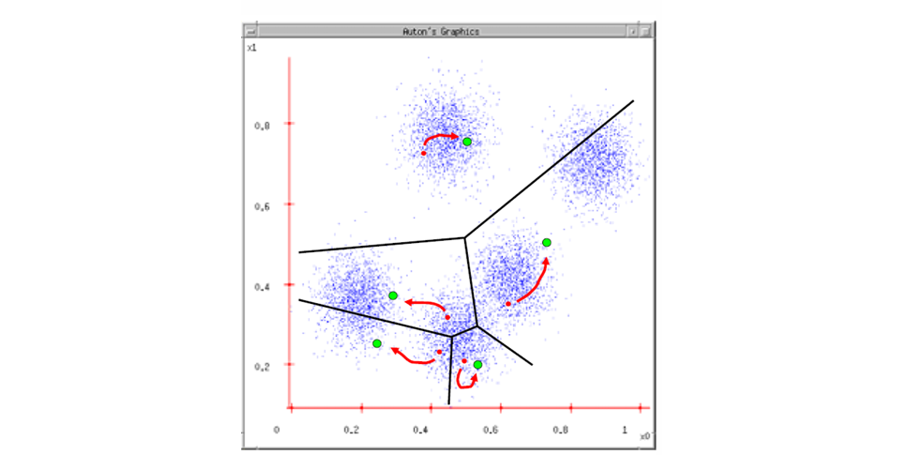
5단계: 반복(Iteration)
할당과 갱신 과정을 반복한다.

중심점이 계속 이동하면서 점차 안정된 위치로 수렴한다.
최종적으로 클러스터 내부는 데이터가 서로 가까우며, 클러스터 간에는 거리가 멀어지게 된다.

6단계: 종료(Termination)
중심점이 더 이상 이동하지 않거나, 이동 거리가 매우 작아지면 알고리즘을 종료한다.

이때의 결과가 최종 클러스터링이다.

K-means는 가까운 중심에 할당 $\to$ 평균으로 중심 갱신 $\to$ 반복의 단순한 원리로 작동한다.

K-means의 한계(Limitation)

K-means 알고리즘은 클러스터 중심을 갱신하면서 수렴하지만, 항상 전역 최적해(global optimum)을 보장하지 않는다. 초기 중심 위치에 따라 결과가 지역 최적해(local optimum)에 빠질 수 있다.

K-Means는 매 반복마다 클러스터 내 제곱 오차 합(SSE)을 줄이는 방향으로만 이동한다. 이 때문에 한 번 잘못된 중심 배치에 빠지면, 더 좋은 해를 탐색하지 못하고 거기서 멈춘다.

K-means의 장단점

장점(Pros)

단순하고 계산 속도가 빠르다.
- 알고리즘 구조가 매우 직관적이고, 반복적인 계산만 포함하므로 대규모 데이터에서도 빠르게 수행할 수 있다.
지역 최소해(Local Minima)에 수렴
- Within-cluster squared error(클러스터 내 제곱 오차합)를 줄이는 방향으로 반복하기 때문에 항상 수렴을 보장한다.
- 전역 최적해는 아닐 수 있지만, 수렴 속도는 빠르다.

단점(Cons/Issues)

K 값을 사전에 설정해야 한다.
- 몇 개의 클러스터가 적절한지 사용자가 미리 알아야 한다. 잘못 설정하면 결과가 크게 왜곡된다.
초기 중심값에 민감하다.
- 초기 중심 선택에 따라 최종 결과가 달라질 수 있으며, 지역 최적해(Local Optimum)에 빠질 위험이 있다. 이를 보완하기 위해 K-means++ 같은 초기화 기법이 제안되었다.
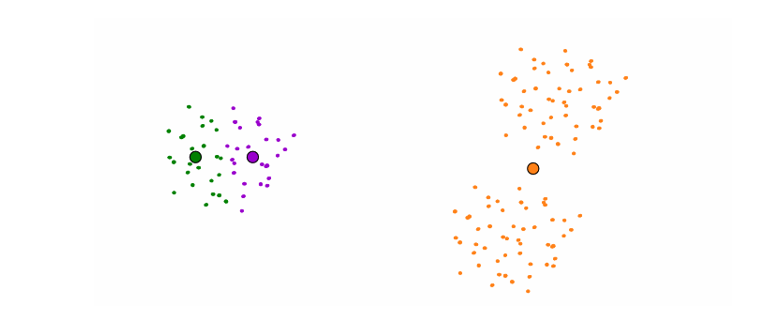
이상치(Outlier)에 민감하다.
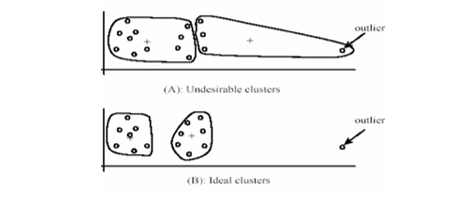
- 평균 기반 알고리즘이므로, 극단적인 값 하나가 클러스터 중심을 크게 왜곡시킬 수 있다.
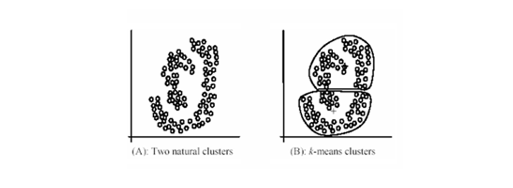
구형(Spherical) 클러스터만 잘 탐지한다.
- 클러스터가 비선형적이거나, 밀도와 형태가 다양한 경우에는 올바르게 분리하지 못한다.
- 예: 두 개의 길게 늘어진 타원형 클러스터 $\to$ K-means는 경계선을 잘못 나눈다.
평균이 정의되지 않는 데이터에는 적용이 불가하다.
- 데이터가 카테고리형(Categorical)일 경우 평균을 정의하기 어렵다.

Segmentation as Clustering

영상 분할을 클러스터링으로 해석하면, 각 픽셀을 특징 공간(feature space)에서 하나의 점으로 보고, 서로 비슷한 점들을 그룹화하여 영역을 나누는 과정이 된다. 이때 어떤 특징을 선택하느냐에 따라 분할 결과가 달라진다.

특징 공간(Feature Space)의 선택
픽셀을 분할하려면 우선 어떤 속성을 비교할 것인지 정해야 한다. 예를 들어 밝기(intensity)를 기준으로 한다면, 픽셀들은 1차원 값(0~255)으로 표현된다. 이 값들을 기준으로 가까운 픽셀끼리 묶으면, 비슷한 밝기 영역이 같은 그룹으로 분류된다.

Intensity 기반 클러스터링

K=2 : 픽셀을 두 그룹으로 묶으면, 밝은 영역(배경/털 일부)과 어두운 영역(눈, 귀, 다리 등)이 나눠진다.
K=3 : 그룹을 세 개로 나누면, 중간 톤의 회색 영역이 추가되어 더 세분화된 결과가 나온다.

즉, 클러스터 수 $K$ 에 따라 결과가 달라지며, 단순히 밝기만으로도 효과적인 분할이 가능하다.

다른 Feature Space 확장
그러나 Intensity만으로는 조명 변화나 복잡한 배경에서 성능이 떨어진다. 그래서 실제 영상 분할에서는 다음과 같은 추가 속성들을 결합한다.

Color(RGB, HSV 등)
- 픽셀을 3차원 색상 공간에서 표현하고, 유사한 색상끼리 묶는다.
- 직관적이고 색상 구분이 잘되나 조명 변화에 민감하다.
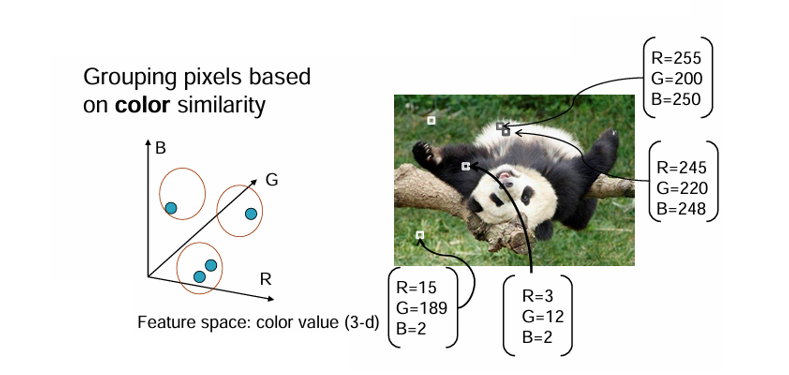
Intensity + Position(밝기 + 좌표(x,y))
- 같은 밝기라도 공간적으로 떨어져 있으면 다른 그룹으로 나눌 수 있다.
- 예: 팬더의 눈과 그림자 영역이 같은 Intensity를 가지더라도, 위치 정보를 포함하면 서로 다른 세그먼트로 분리된다.
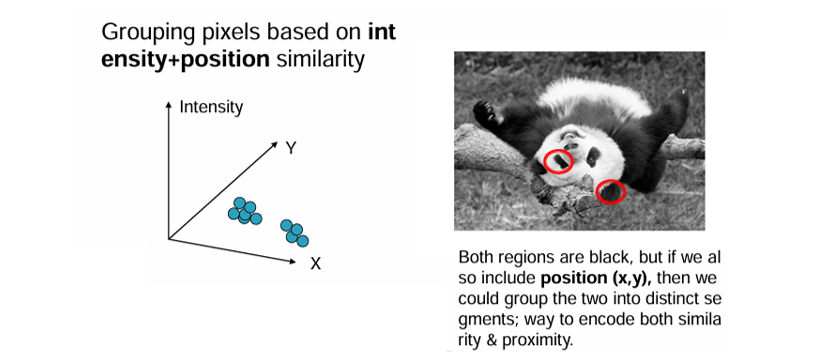
Texture(질감)
- 필터 뱅크(filiter bank)나 가버 필터를 적용해, 픽셀의 질감을 벡터로 표현한다.
- 색상 $\cdot$ 밝기가 비슷해도, 머리카락 $\cdot$ 피부 $\cdot$ 옷처럼 질감이 다르면 별도의 그룹으로 분할할 수 있다.

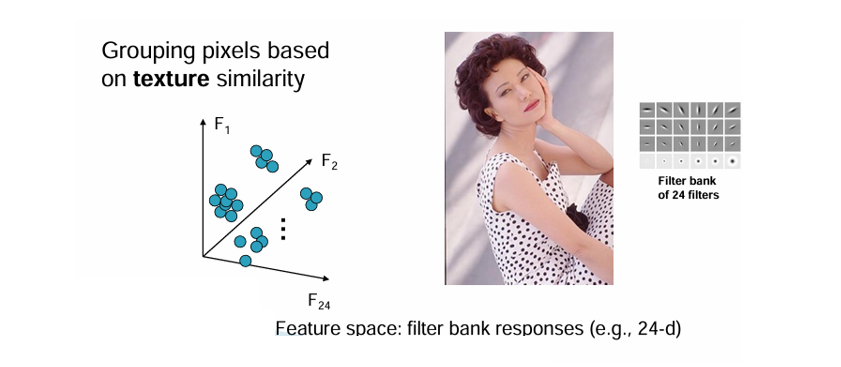
Segmentation as Clustering의 장점은 객체에 대한 사전 지식 없이, 픽셀의 유사성을 기반으로 분할할 수 있다. 하지만 단순 Intensity 기준은 조명 변화나 복잡한 배경에 취약하다. 따라서 실제로는 intensity 외에도 색상(color), 위치(x,y), 질감(texture) 같은 다양한 특징을 조합해 클러스터링 한다.

Mean Shift Clustering

영상 분할에서 클러스터링은 픽셀들을 특징 공간(feature space)에 배치한 뒤, 서로 유사한 속성을 가진 픽셀들을 하나의 그룹으로 묶는 방식이다. 이 과정에서 K-means가 널리 사용되지만, K-means는 클러스터 개수 $K$ 를 사전에 지정해야 하고, 데이터가 비선형적이거나 복잡한 구조를 가질 경우 한계가 존재한다. 이러한 문제를 보완하기 위해 제안된 기법이 바로 Mean Shift Clustering이다.

Mean Shift의 기본 아이디어

Mean Shift는 데이터의 밀도(density) 분포를 기반으로 고밀도 영역을 찾아내는 비모수(non-parametric) 기법이다. 즉, 클러스터의 개수를 미리 지정할 필요가 없으며, 데이터가 많이 모여 있는 영역을 모드(mode, 국소 최대치)로 정의하여 자동으로 그룹을 형성한다.

알고리즘은 각 데이터 포인트를 중심으로 일정 크기의 윈도우(Window)를 두고, 그 안의 평균(mean)을 계산한다. 이후 윈도우를 평균 위치로 이동시키는 과정을 반복하면서 점차 밀도가 높은 영역으로 수렴한다. 결국 모든 데이터 포인트는 특정 모드에 도달하게 되고, 같은 모드로 수렴한 포인트들은 동일한 클러스터에 속하게 된다.

Mean Shift Algorithm

임의의 데이터 포인트를 초기 seed로 선택하고, 윈도우 $W$ 를 설정한다.
윈도우 안에 포함된 데이터들의 평균값을 계산한다.
윈도우 중심을 이 평균 위치로 이동시킨다.
수렴할 때까지 위 과정을 반복한다.
같은 모드로 수렴한 점들을 하나의 클러스터로 묶는다.

이 과정은 수식으로 다음과 같이 표현된다.

m(x) = \frac{\sum_{i=1}^n K(x_i - x)x_i}{\sum_{i=1}^n K(x_i - x)} - x

여기서 $K$ 는 커널 함수(보통 가우시안), $x_i$ 는 데이터 포인트, $x$ 는 현재 위치이다.

영상 분할에서의 Mean Shift
영상 분할에 Mean Shift를 적용할 때는 픽셀의 색상(color), 위치(x,y), 질감(texture) 등의 특징을 함께 고려한다.

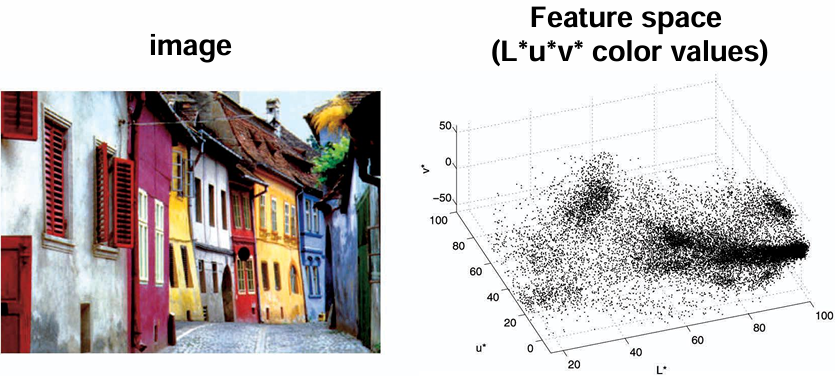
예를 들어 위 그래프와 같이 색상 공간(Luv*)에 투영된 데이터를 보면, 유사한 색을 가진 픽셀들이 특정 영역에 밀집하게 된다. Mean Shift는 이 모드들을 자동으로 찾아내어 색상 단위로 객체를 분리한다.

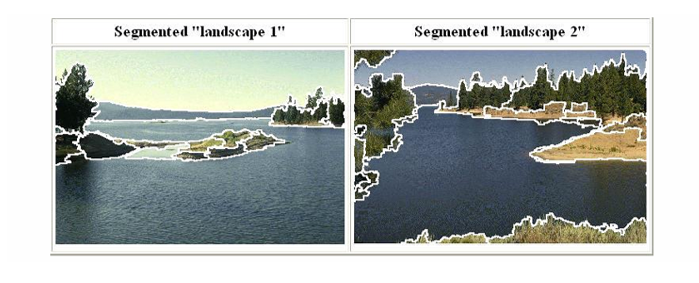
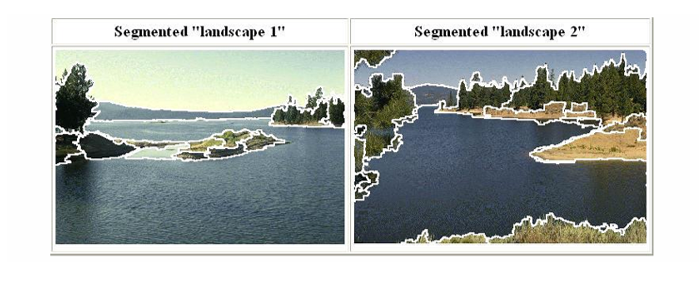
실제 풍경 이미지를 분할한 예시를 보면, 하늘, 산, 숲, 강 같은 영역이 자연스럽게 구분된다. K-means처럼 단순히 색상 값만 반영하는 것이 아니라, 공간적 근접성과 색상 분포를 동시에 고려하기 때문에 객체 경계를 더 잘 반영한다.

Mean Shift는 밀도 기반 클러스터링 기법으로, 객체와 배경을 자동으로 구분하는 강력한 분할 도구이다. K-means가 단순하고 빠른 장점이 있지만, 클러스터 개수를 직접 지정해야 한다는 제약을 가진 반면, Mean Shift는 데이터가 스스로 말해주는 구조를 찾아내는 방식이다. 따라서 영상 분할에서는 특히 자연 영상이나 복잡한 장면에서의 객체 분리에 효과적이다.

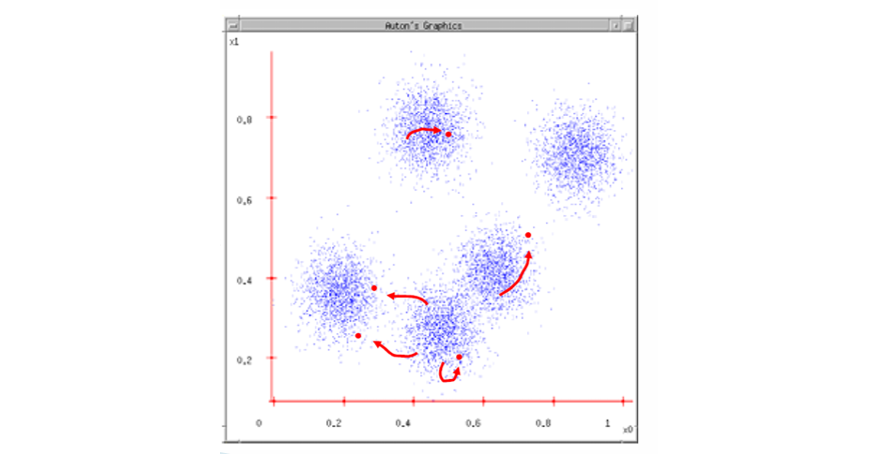
Mean Shift Algorithm의 시각적 이해

Mean Shift는 데이터 분포에서 고밀도 영역(모드, mode)을 찾는 알고리즘이다. 각 점에서 출발해 주변 데이터를 고려한 평균 방향으로 반복 이동하면서, 최종적으로 밀도가 가장 높은 위치에 수렴한다.

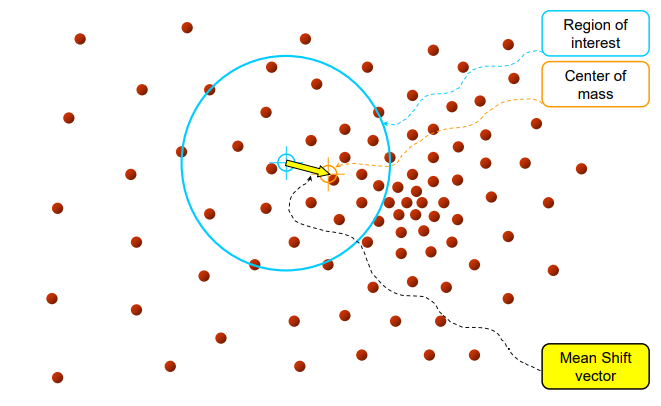
1단계: 초기 윈도우 설정
아래 이미지의 파란색 원이 Search Window(탐색 창)이다. 시작점(파란색 십자 표시) 주변의 데이터(갈색 점들)를 모아서 윈도우 안에 포함시킨다.

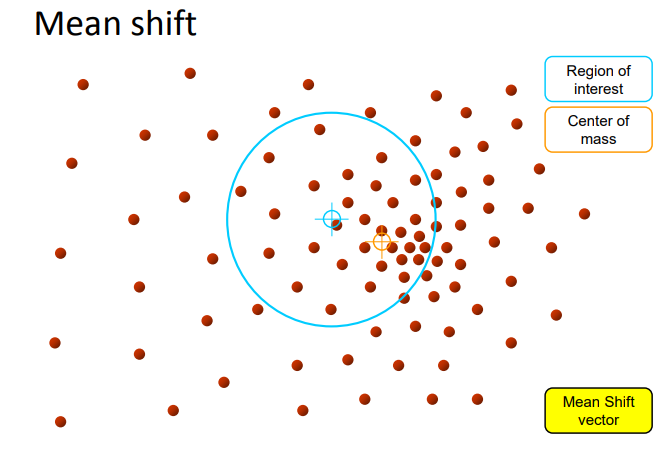
2단계: 질량 중심 계산(Center of mass)
탐색 윈도우 안의 데이터들의 평균 위치를 계산한다. 이 평균이 주황색 십자로 표시된 Center of mass이다. 평균이 현재 윈도우 중심보다 오른쪽 아래쪽에 치우쳐 있다면, 데이터가 그 방향으로 더 많이 밀집해 있다는 의미이다.

3단계: Mean Shift 벡터 이동
현재 윈도우 중심에서 평균 위치까지의 이동 벡터(노란색 화살표)를 계산한다. 이 벡터가 Mean Shift Vector이다. 중심을 평균 위치로 이동시키고, 탐색 윈도우도 같이 이동한다.

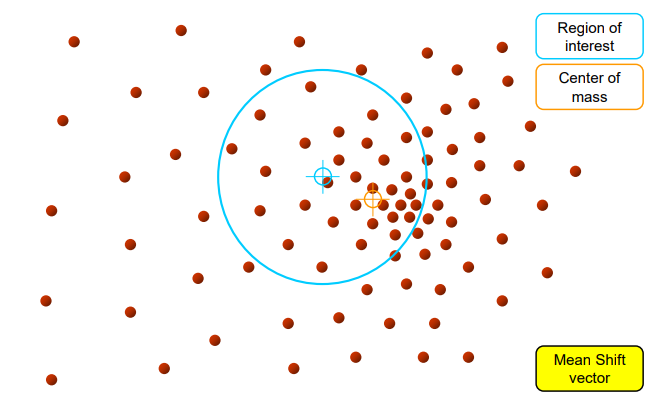
4단계: 반복 이동
새롭게 이동한 위치에서 다시 윈도우 안의 질량 중심을 구한다. 이후 또 다시 중심을 이동시켜 윈도우를 업데이트한다.

이 과정을 반복하면서 점차 데이터가 더 밀집된 방향으로 이동한다.

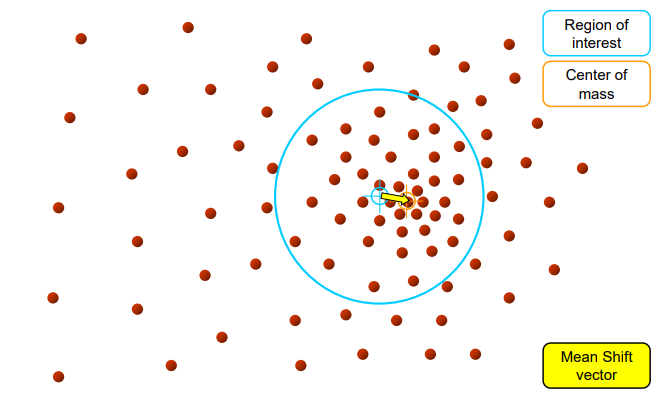
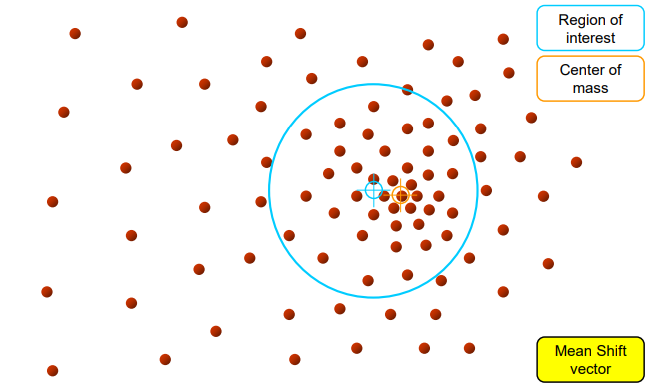
5단계: 수렴
중심이 더 이상 크게 이동하지 않으면, 해당 위치가 밀도 최대치(모드, local maximum)이 된다. 결국 모든 데이터 포인트가 주변 윈도우를 따라 움직이면서 고밀도 영역(클러스터 중심)에 모이게 된다.

같은 모드로 수렴한 데이터들은 하나의 클러스터를 형성한다.

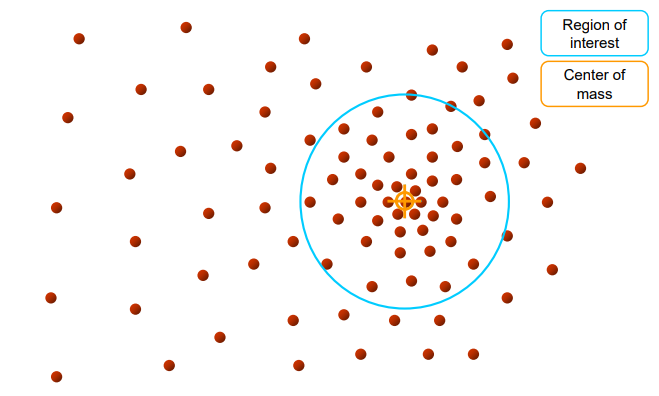
Mean Shift Clustering

Mean Shift에서 하나의 클러스터(Cluster)는 특정 모드(mode, 밀도 최대치)에 수렴하는 모든 데이터 포인트들의 집합으로 정의된다.

Cluster : 같은 모드에 도달한 모든 데이터 포인트
Attraction basin(끌림 영역) : 데이터 분포에서, 어느 지점에서 출발하더라도 같은 모드로 수렴하는 영역

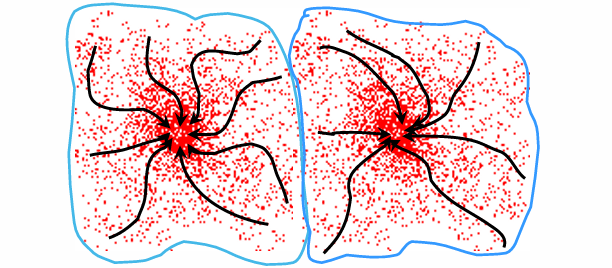
위 그림을 보면, 데이터 포인트들이 두 개의 고밀도 영역에 모여 있고, 각각의 점들이 곡선을 따라 중심으로 이동하여 결국 두 개의 클러스터가 형성된다.

즉, 클러스터는 단순히 평균 거리 기반이 아니라, 밀도 기반의 흡인 영역으로 정의된다는 것이 K-means와의 큰 차이점이다.

Mean Shift Clustering/Segmentation 절차

영상 분할에서 Mean Shift를 적용할 때의 단계는 다음과 같다.

1. 특징 추출(Find features)

픽셀로부터 색상(color), 그래디언트(gradient), 질감(texture) 등의 특징을 뽑는다.
이 특징들은 고차원 feature space의 좌표로 표현된다.

2. 윈도우 초기화(Initialize windows)

각 특징 벡터(픽셀)마다 초기 윈도우를 설정한다.
윈도우는 해당 픽셀 주변의 데이터 분포를 탐색하기 위한 시작점이다.

3. Mean Shift 반복 수행(Perform mean shift until convergence)

각 윈도우는 탐색 과정에서 점차 데이터가 밀집된 방향으로 이동한다.
수렴할 때까지 반복하면, 윈도우 중심은 결국 밀도 최대치(peak)에 도달한다.

4. 모드 병합(Merge Windows at the same mode)

서로 다른 초기점에서 출발했더라도, 같은 peak로 수렴한 윈도우들은 동일한 클러스터로 병합된다.
최종적으로, feature space가 여러 클러스터로 나뉘고, 이를 영상의 영역 분할로 해석할 수 있다.

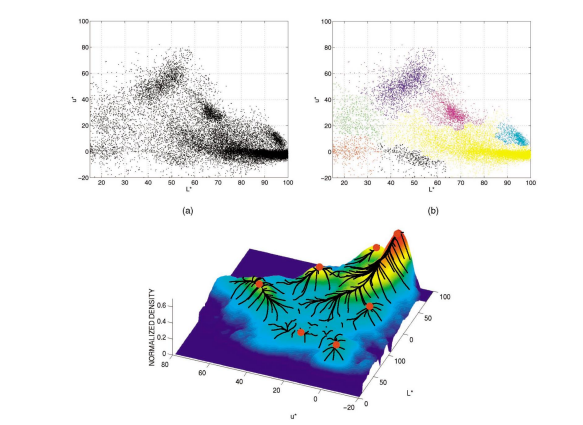
왼쪽 상단 그래프는 초기 feature space로 데이터 포인트가 흩어져있는 모습을 확인할 수 있다.

Mean Shift 수행 후 우측 상단 그래프를 보면, 색상별로 구분된 영역이 각각 다른 모드에 수렴함을 확인할 수 있다.

하단의 그래프는 3D 밀도 그래프로 데이터가 밀집된 지역(peak)으로 포인트들이 이동하는 과정을 보여준다.

결국 Mean Shift는 단순한 거리 기반 분할이 아니라 데이터의 밀도 구조를 고려한 분할 기법이다. 영상 분할에서는 픽셀들의 유사성이 아닌, "픽셀들의 집합이 어떤 밀도 구조에 속하는가"로 구분하기 때문에 경계가 더 자연스럽게 형성된다.

Mean Shift Segmentation Results

Mean Shift Pros and Cons

Pros

범용적이고 응용 독립적(General, application-independent) : 특정 분야에 국한되지 않고, 다양한 데이터 분석과 영상 분할 문제에 적용할 수 있다.
모델 가정이 필요 없음(Model-free) : K-means처럼 클러스터가 구형(spherical)일 것이라는 가정을 하지 않는다. 즉, 데이터가 어떤 형태(원형, 타원형, 비선형 구조)든 그대로 반영할 수 있다.
단일 파라미터(윈도우 크기 h)만 필요 : Mean Shift는 클러스터 개수를 직접 지정할 필요가 없고, 대신 윈도우 크기 $h$ 하나만 정하면 된다. 이 $h$ 는 데이터에서 물리적 의미를 가지며, 탐색 범위를 직관적으로 나타낸다.
변동적인 클러스터 수 자동 탐지(Variable number of modes) : 데이터 분포에 따라 클러스터 개수가 자동으로 결정된다. K-means와 달리 사전에 K를 정하지 않아도 된다.
이상치(Outlier)에 강건(Robust to outliers) : 밀도 기반 탐색이므로, 극단적인 데이터 포인트가 결과에 큰 영향을 주지 않는다.

단점(Cons)

윈도우 크기에 의존적(Depends on window size) : 결과는 윈도우 크기 $h$ 를 어떻게 설정하느냐에 따라 크게 달라진다.
윈도우 크기 선택이 어렵다(Bandwidth selection not trivial) : 최적의 $h$ 를 선택하는 것은 쉬운 일이 아니며, 데이터마다 적절한 값이 다르다. $h$ 가 너무 크면 클러스터가 합쳐지고, 너무 작으면 잡음까지 클러스터로 인식한다.

Mean Shift는 클러스터 개수를 알 수 없거나 데이터 구조가 복잡한 상황에서 매우 유용한 방법이다. K-means보다 더 일반적인 상황에 적용할 수 있고, 특히 영상 분할에서 객체 단위로 영역을 나누는 데 효과적이다. 하지만 윈도우 크기 선택 문제가 여전히 중요한 과제로 남아 있으며, 실제 응용에서는 교차 검증이나 경험적 기준을 사용해 ℎ를 정하는 경우가 많다.

References

Slide credit: Svetlana Lazebnik
Slide by Y. Ukrainitz & B. Sarel
Slide credit: Kristen Grauman
Slide credit Andrew Moore

http://www.caip.rutgers.edu/~comanici/MSPAMI/msPamiResults.html
D. Comaniciu and P. Meer, Mean Shift: A Robust Approach toward Feature Space Analysis, PAMI 2002.