1. Linear combination

think of each coordinate as a scalar

• 각각의 좌표값
  : 벡터를 어떻게 늘리고 줄일지에 대한 정보임.
  • 좌표값은 스칼라라고 생각하기

xy좌표계에서의 두가지 벡터

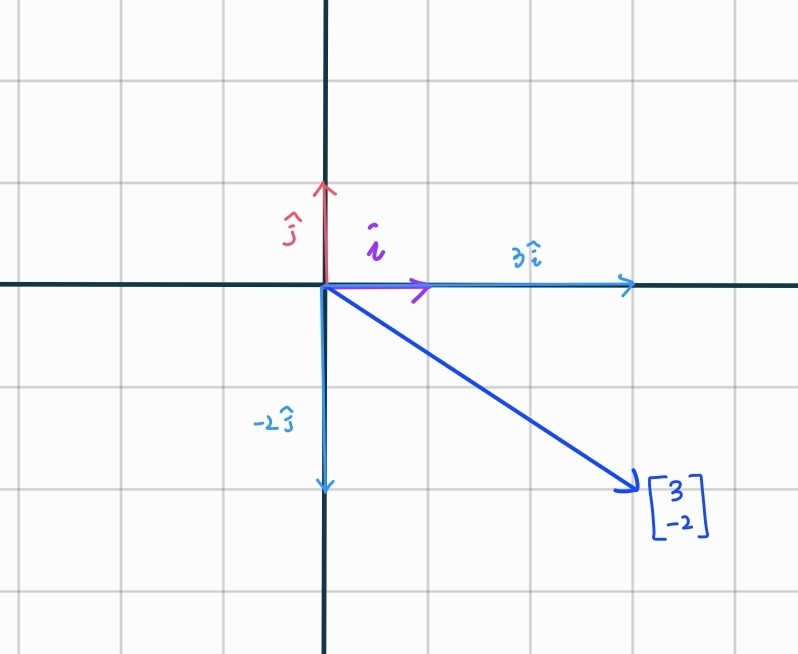
1. 아이-헷(i-hat)
   : 오른쪽 방향의 길이 1벡터
   • x축의 단위 벡터(unit vector)
2. 제이-헷(j-hat)
   : 위쪽 방향으로 길이 1인 벡터
   • y축의 단위 벡터(unit vector)

i-hat and j-hat are the 'basis vectors(기저 벡터)' of the xy coordinate system

• basis vector: 스칼라(좌표값)가 스케일링 하는 대상

→ 좌표계를 특별한 이 기저벡터 두개로 구성(framing)하는 것

what if we chose different basis vectors?

: 또 하나의 완전한 새 좌표계를 얻게 된다.

• 모든 2차원 벡터들이 가능함.

• 수치로 벡터를 표현할 때, 암묵적으로 특정 기저 벡터들을 선택한 상태라는 것.

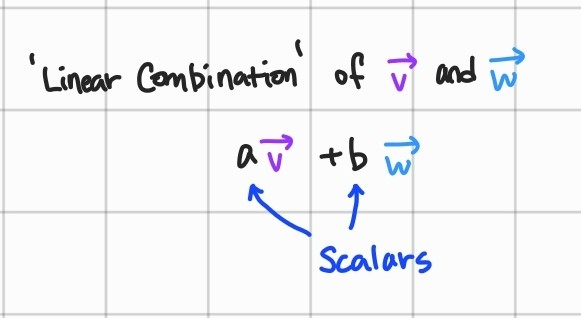
• 두 벡터를 스켈링하고 나서 더하는 것
  = 두 벡터의 선형조합(linear combination)
  

2. 스팬(span)

• span
  : 어떤 공간을 포괄하다, 벡터들로 형성할 수 있는 공간
  = v와 w의 선형조합을 통해 만들어지는 공간
  
• 2차원의 벡터쌍의 스팬(span)은 대부분의 경우 2차원 공간 전체가 되지만, span이 특정 선 위로 제한되는 경우도 있음.
  • 선형대수: 벡터합과 스칼라곱의 주위를 돌며 이뤄진다.
  • 오로지 두 가지 기본 연산(벡터합과 스칼라곱)을 가지고 도달 가능한 벡터들의 집합

Vectors vs. Points

• 하나의 벡터를 생각할 때
  : 하나의 화살표로 생각하는 것이 좋음.
  Think of individual vectors as arrows
• 벡터의 집합을 다룰 때
  : 모든 점들로 생각하는 것이 좋음.
  Think of sets of vectors as points

what does the span of two 3d vectors look like?

• span: 두 벡터의 모든 선형조합의 결과
  = 두 벡터를 벡터합과 스칼라곱을 통해 조합해서 만들 수 있는 모든 벡터들을 의미함.
• 두 스칼라들로 두 스케일링 된 벡터의 합에 영향을 주고, 따라서 결과 벡터의 끝에도 영향을 줌
• 그 끝은 3차원 공간의 원점을 가로지르는 평평한 공간이 됨.
  = 이 평면이 두 벡터의 스팬(span, 확장공간)
  = 평면위에 끝(tip)을 놓는 모든 벡터들의 집합이 두 벡터의 스팬

Q. 세 벡터의 선형조합은?

: 두 벡터의 선형조합과 거의 비슷함

두가지 차이점

1. 세번째 추가한 벡터가 다른 두 벡터가 만드는 스팬(span, 여기선 평면)에 놓여있다면, 세번째 벡터를 추가해도 스팬이 바꾸지 않음
   = 똑같은 평면에 그대로임.
2. 두 벡터의 스팬평면에 놓여있지 않은 벡터를 선택한다면, 새로운 방향을 가리키는 것이 가능해져 3차원의 모든 벡터들에 대한 접근이 가능해진다.

idea

1. 세번째 벡터를 스케일링 해보면서 기존 두 벡터의 스팬 평면위에 갇혔는지 확인해본다.
2. 스칼라를 마음것 변화시켜서 3차원 공간 전체에 대해 접근가능한지 판단해본다.

선형 종속(linear dependent)

: 스팬의 축소없이 하나 이상의 벡터를 제외시켜도 되는 경우(차이점1)

• 벡터들 중 하나가 다른 벡터들의 선형조합으로 표현가능한 경우
• 이미 다른 벡터의 스팬에 포함되는 경우

선형 독립적(linear independent)

: 각각의 벡터가 기존 스팬에 또 다른 차원을 추가해주는게 가능한 경우(차이점2)

3. basis

Technical definition of basis

: The basis of a vector space is a set of linearly independent vectors that span the full space