Matrices as Linear transformations

Linear transformation(선형변환)

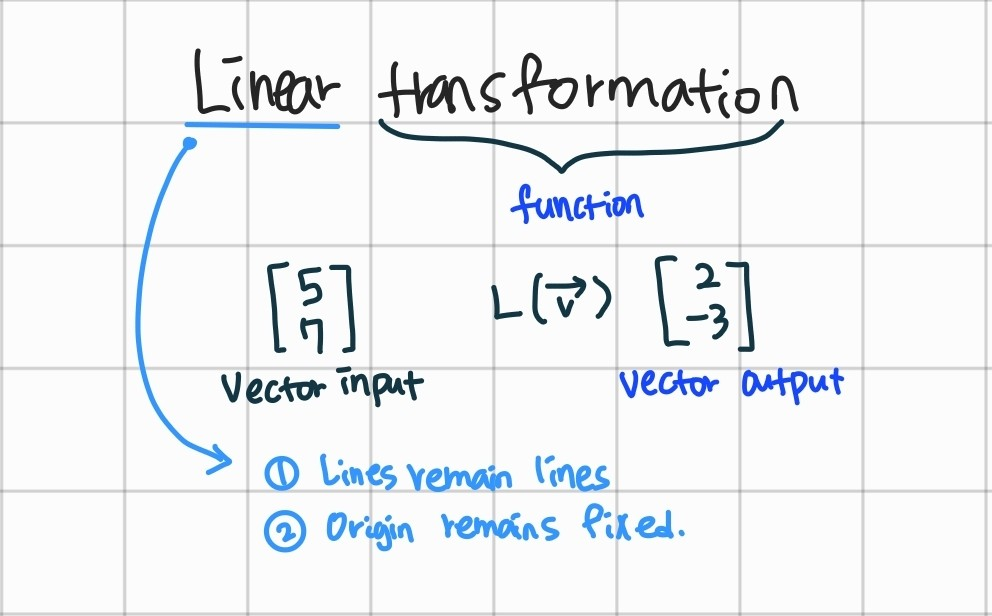
1. transformation
   : 함수(function)의 다른말
   : 입력을 받고 결과물을 반환하는 그 무엇

• 선형대수 맥락으로의 transformation
  • 특정 벡터를 다른 벡터로 바꾸는 변환같은 것

2. 'function' 대신 'transformation' 사용 이유
   : 입력 - 출력 관계를 시각화하는 특정 방법을 암시해줌
   • input vector, output vector 생각할 때 공간상의 모든 점들이 다른 점으로 이동하는 것처럼 생각하면 됨.
3. linear(선형적)
   : 변환이 선형적 하다는 것은 두 가지 속성을 의미함
   • 모든 선들은 변환 이후에도 휘지 않고 직선이어야한다.
   • 원점은 변환 이후에도 여전히 원점이어야한다.

※ 선형 변환
: 격자 라인들이 변형 이후에도 여전히 '평행'하고 '동일한 간격'으로 있어야함.
Grid lines remain paralle and evenly spaced

how wold you describe one of these numerically?

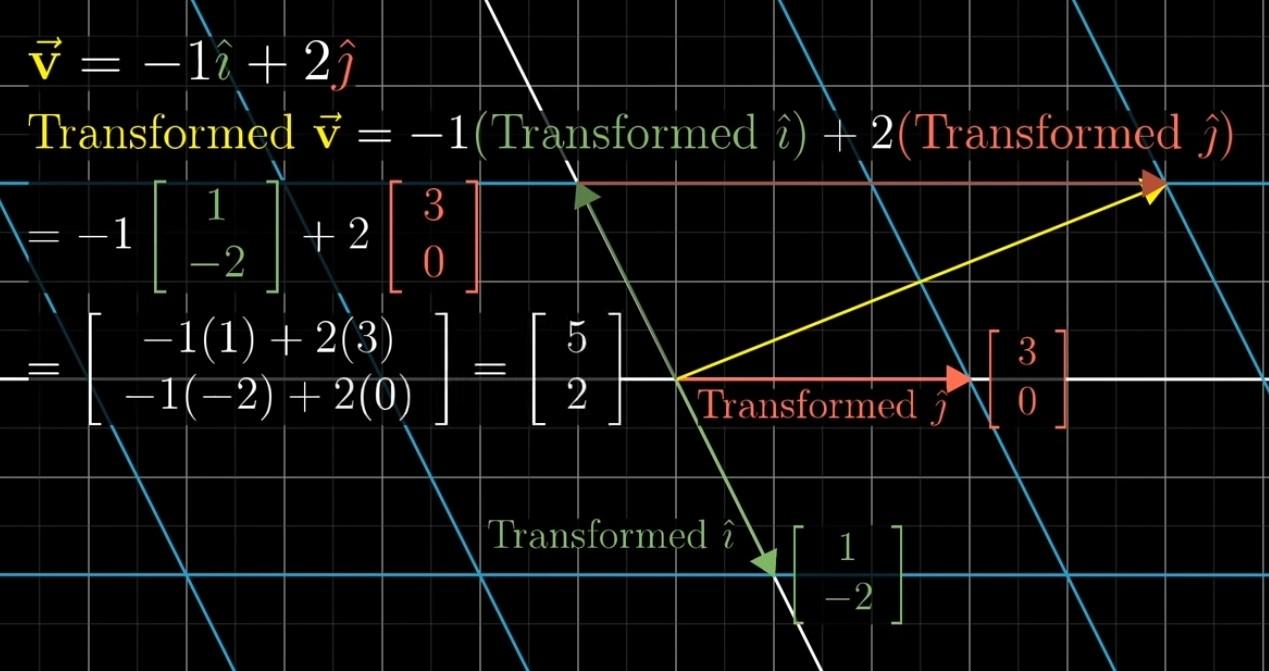
: 두 개의 기저벡터(i-hat, j-hat)가 어떻게 변하는지만 알면 해결된다.

• 단순히 i-hat과 j-hat의 변형위치만 알면, 벡터 v를 추론할 수 있다는 것을 의미한다.
• 일반화
  

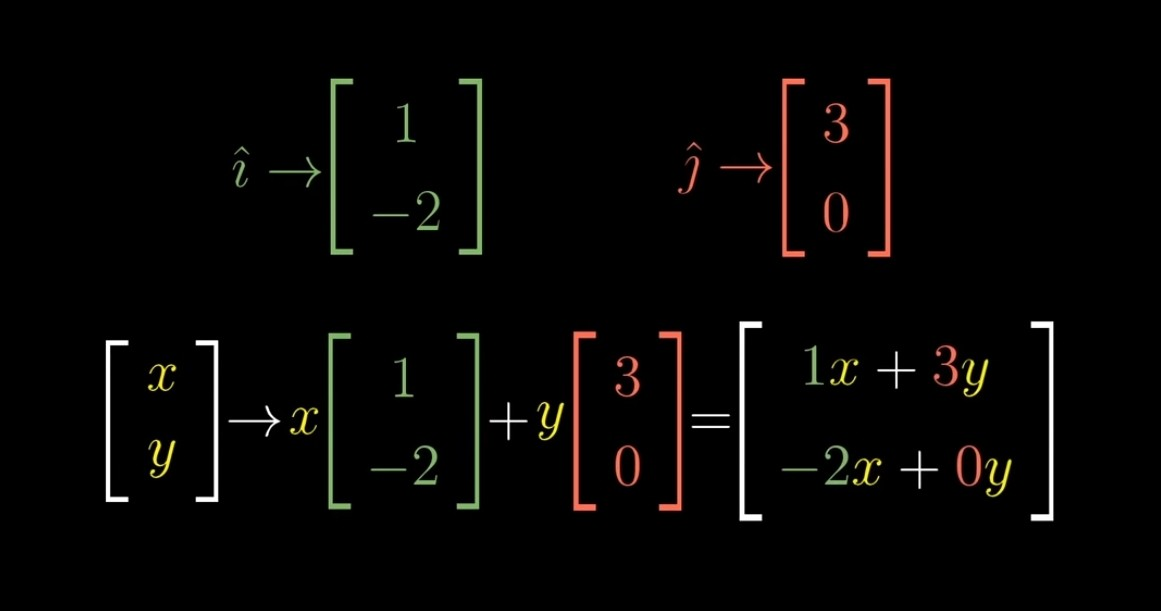
→ 2차원 선형 변환을 통해 모든것들이 오로지 4개의 숫자면 설명이 가능하다.

• 변환된 i-hat의 두개의 좌표값

• 변환된 j-hat의 두개의 좌표값

  ex. i-hat(3,-2) / j-hat(2,1)
  

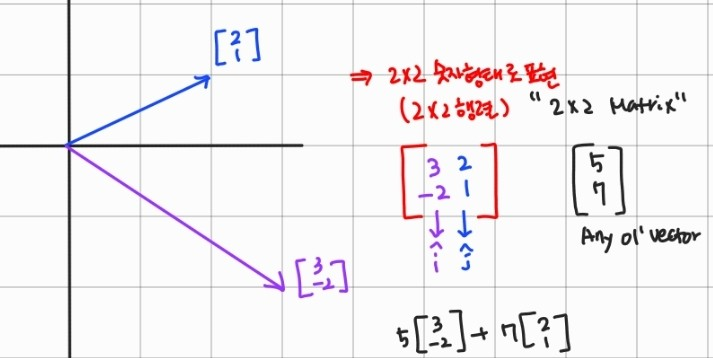
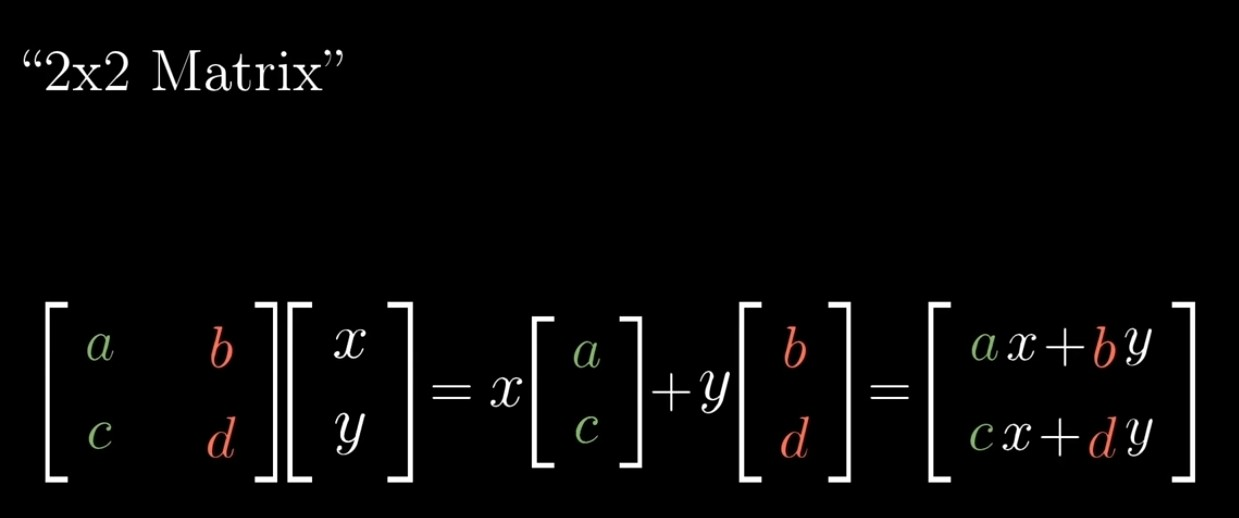
  • 일반화: 행렬x벡터
    
    

Shear

• i-hat은 고정되어 있고 j-hat만 movement

linear transformation의 정의

: 격자선이 평행하고 균등간격으로 유지한 변형
: 원점은 고정되어 있음
: 기저 벡터들의 변형 후 좌표값으로 설명가능

• 2X2 Matrix로 표현가능
  • 행렬의 열: 기저벡터의 좌표값을 나타냄
  • 행렬-벡터 곱: 이 변환이 주어진 벡터에 적용한 결과를 단지 계산하는 방법임