선형 변환의 합성
'Composition' of a rotation and a shear
- 다른 선형변환과 마찬가지로 행렬로 표현이 가능
- i-hat, j-hat 이용
- i-hat의 최종 도착지
: (1,1) - j-hat의 최종 도착지
: (-1,0)
- i-hat의 최종 도착지
- 수치적 표현
: 회전 시키고 민 것의 수치적 표현
= 행렬의 곱과 같은 결과가 나옴
→ 우리가 구한 새 행렬이 회전하고 민 것과 같은 효과를 나타냄
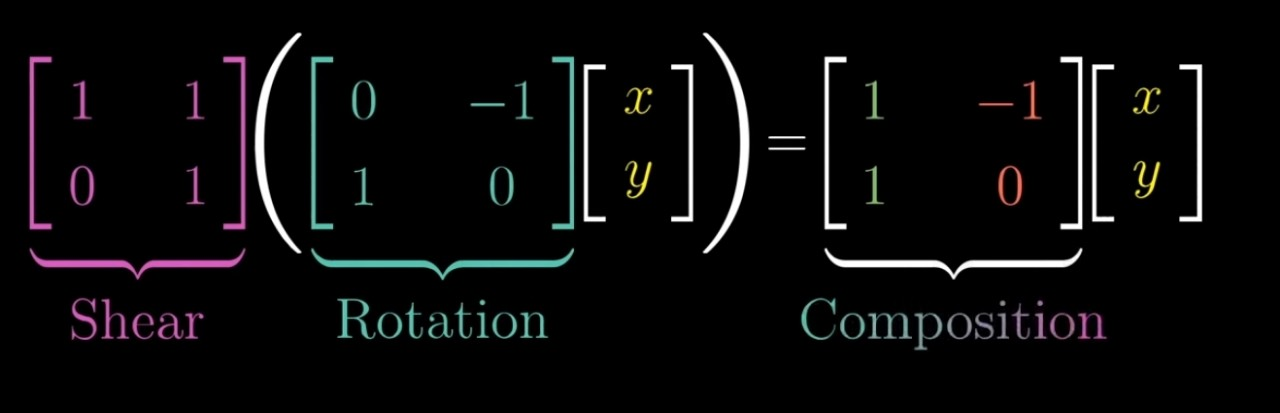 ▶ 새 행렬 = 두 원본 행렬의 곱(product)
▶ 새 행렬 = 두 원본 행렬의 곱(product)
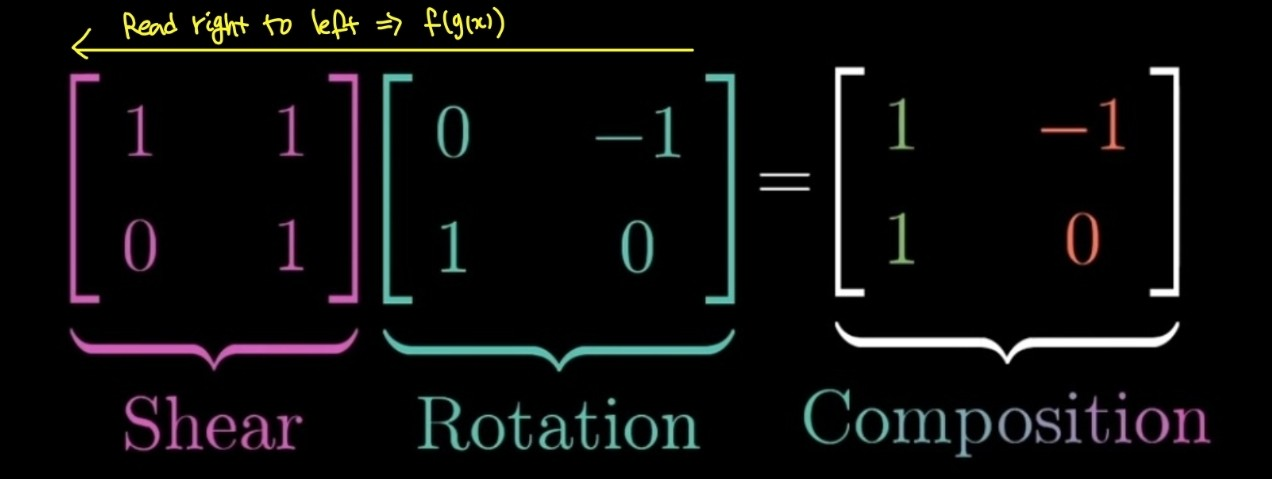
- 우측의 행렬
: 첫번째 반환을 의미 - 좌측의 행렬
: 그 다음 변환 적용을 나타냄
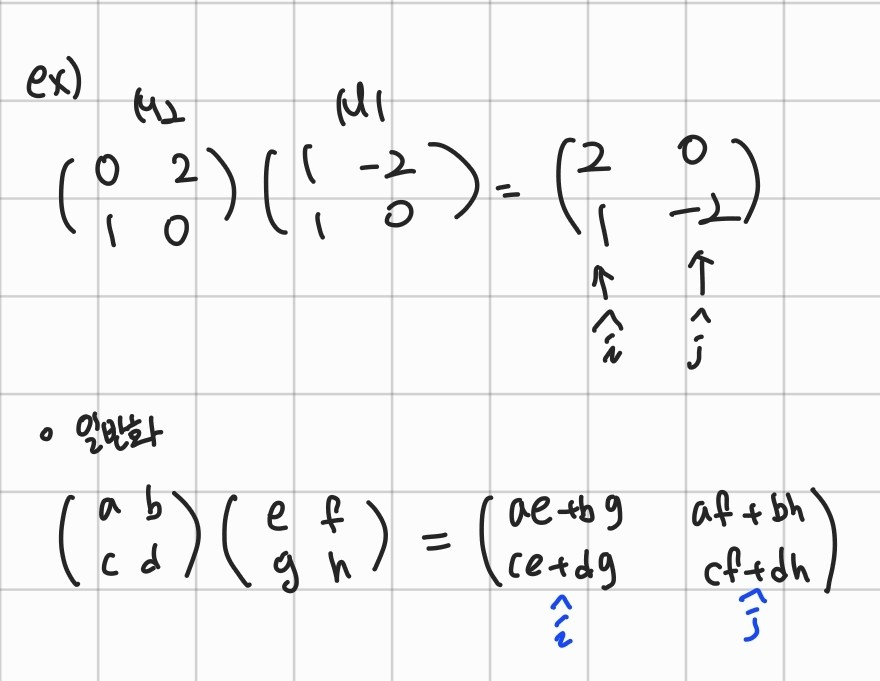
- i-hat, j-hat 이용
Q1. 두 행렬을 곱할 때 그 두 행렬을 곱하는 순서가 상관 있을까?
: 상관있다
: 곱하는 순서에 따라 결과가 달라지기 때문에 곱하는 순서가 중요한다.
- 서로 다른 두 개의 변환을 떠올려서 한 변환을 적용한 후 다른 변환을 적용하는 것으로 하면 행렬의 결합법칙 간단히 증명 가능