아래는 Xiang Gao와 Tao Zhang의 <Introduction to Visual SLAM>을 읽고 번역정리+추가적인 코멘트를 단 내용이다.
말은 가능하면 간소화하고, 이론적으로 더 참고할만한 부분은 추가적인 코멘트를 넣었음.
저자에 의해 모든 자료가 무료 배포되었음. 아래 링크 참고
📘 영어판 도서 파일: https://github.com/gaoxiang12/slambook-en
📂 practice 코드: https://github.com/gaoxiang12/slambook2

1장. Introduction to SLAM

🔎 학습 목표
1. Visual SLAM 프레임워크가 어떤 모듈들로 이루어지고, 각 모듈이 어떤 역할을 하는지 이해한다.
2. 프로그래밍 환경을 셋팅하고, 실험을 위한 준비를 완료한다.
3. 리눅스에서 프로그램을 어떻게 컴파일하고 실행하는지 이해한다. 만일 컴파일 단계에서 문제가 생긴다면 어떻게 디버깅하는지 배운다.
4. CMake의 기본 사용법을 배운다.

이번 강의에서는 따라오는 챕터에서 다룰 내용들의 개요를 잡는 느낌으로 visual SLAM 시스템의 구조를 요약 설명할 것이다. 실습 파트에서는 환경 설정과 프로그램 개발에 대한 기초를 설명한다. 깜찍한 "Hellow SLAM" 프로그램을 만들어보는 것으로 마무리!

1.1 "Little Carrot"을 만나보자

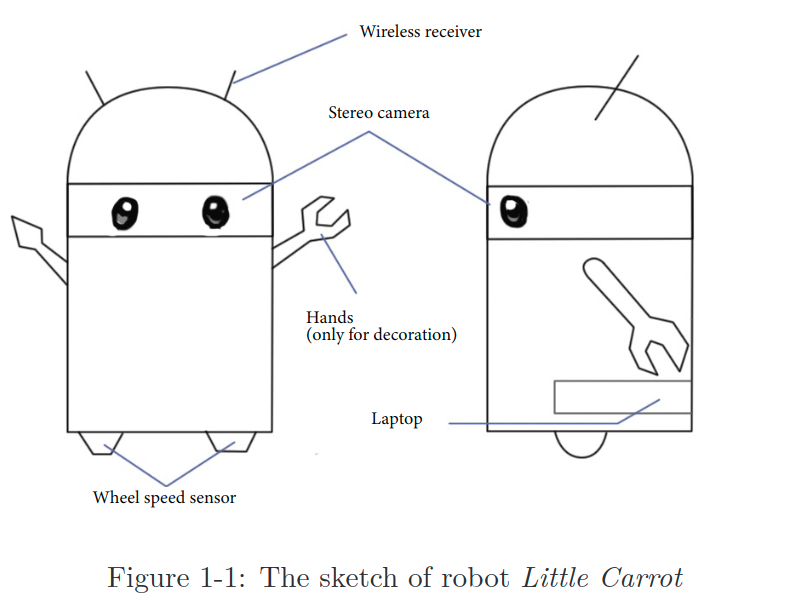
위는 Little Carrot이라는 이름을 가진 귀여운 로봇이다.
이 친구가 방 안에서 자유롭게 돌아다닐 수 있도록 자율주행 기능을 탑재해보자.
바퀴만으로도 돌아다니는 것은 가능하지만, 적절한 네비게이션 시스템 없이는 여기저기 부딫혀 물건을 망가뜨릴 수도 있다. 머리에 카메라 두개를 달아주어 Little Carrot이 두 눈과 머리, 사지가 있는 사람의 형상을 갖추도록 디자인해보자. 이제 Little Carrot은 사람처럼 자유롭게 돌아다니면서 환경을 탐색할 수 있을까? 그러기 위해서는 Little Carrot은 최소한 아래 두 가지를 스스로 알 수 있어야 한다.

• 내 위치가 지금 어디쯤인지 (=localization)
• 현재 나를 둘러싼 환경이 어떻게 생겼는지 (=map building)

이 두 문제를 풀기 위해선 바닥에 가이드 레일을 깔아 그 위만 주행하도록 한다든가, QR 코드같은 마커를 벽에 덕지덕지 붙인다든가, radio localization 기기를 테이블에 부착한다든가 하는 여러가지 접근 방법들이 있을 수 있다. 실외환경이라면 Little Carrot의 머리에 휴대폰이나 차량에 부착하는 GNSS 수신기를 설치해줄 수도 있을 것이다.

위 그림에서 보이는 여러가지 센서들은 침입형(intrusive)/비침입형(non-intrusive) 두 가지 카테고리로 나뉜다. 비침입형 센서는 로봇 몸체에 부착하기만 하면 환경과는 관계없이 활용 할 수 있는 휠 인코더, 카메라, 레이저 센서, IMU 등을 의미한다. 침입형 센서는 로봇이 아닌 환경에 설치해야하는 가이드 레일이나 QR 코드 등을 말한다. 침입형의 경우 설치가 가능하기만 하다면 localization 문제를 매우 간단하고 정확하게 해결할 수 있지만 범용성이나 사용성의 한계로 인해 활용에 제약이 생길 수 밖에 없다. 만약 GPS 수신을 받을 수 없는 상황이라거나 가이드 레일을 깔 수 없는 상황이라면 어떡할 것인가?
반대로 비침입형 센서의 경우 직접적인 위치 파악이 불가하고 간접적인 물리적 측정치만을 얻을 수 있다. 예를 들어 휠 인코더는 휠 회전각을 측정하고, IMU는 각속도와 각가속도를 측정한다. 카메라나 레이저 스캐너는 점군이나 이미지와 같은 특정 형식으로 외부환경을 관측한다. 우리는 이러한 간접적인 관측치로부터 위치를 추정하기 위해 여러 복잡한 알고리즘들을 적용해야 한다. 이렇게만 들으면 침입형 센서를 이용한 방식에 비해 엄청 돌아가는 것처럼 보이지만, 이 방식의 분명한 이점은 환경에 대한 요구사항이 없기 때문에 어떤 미지의 환경에서도 적용이 가능하다는 것이다. 이런 특성으로 인해 여러 연구에서 이 비침입형 센서를 이용한 localization 방식을 self-localization이라고 명명하기도 한다.

다시 앞에서 얘기한 SLAM의 정의로 돌아가보면, 우리는 사전 정보가 없는 미지의 환경을 탐색하는 것이 SLAM의 핵심이라고 말한 바 있다. 이론적으로는, Little Carrot이 놓일 환경이 어떤 환경일지 미리 추정하지 않아야 하므로 (물론 실제로는 실외인지 실내인지 정도의 대략적인 범위는 주어질 것이다) 우리는 GPS 같은 외부 센서가 잘 작동할 것이라고 가정해서는 안된다. 따라서 이 책에서는 비침입형 센서를 사용해 SLAM을 수행하는 것에 초점을 맞추며, 그 중에서도 우리는 visual SLAM에 대해서 다루고 있으므로 Little Carrot의 두 눈으로 무엇을 할 수 있는지를 중점적으로 알아 볼 것이다.

SLAM에서 쓰이는 카메라는 보통의 SLR (single-lens reflex) 카메라와는 차이가 있다. 훨씬 저가이며, 비싼 렌즈를 사용하지 않는다. 또한 일정 속도(보통의 경우 30fps)로 연사하여 연속적인 비디오 스트림 형태의 데이터를 생성한다. 카메라는 아래 그림과 같이 크게 세 가지 카테고리로 나뉜다; monocular (단안), stereo (양안), RGB-D.

이름에서 직관적으로 알 수 있듯이, 단안 카메라는 하나의 카메라만을 가지고 있고, 양안 카메라는 카메라 두 개로 이루어져있다. RGB-D 카메라의 원리는 좀 더 복잡한데, 컬러 이미지를 찍는 것 뿐만 아니라 각 픽셀에 대해 씬과 카메라 사이의 거리를 측정해준다. 자세한 원리는 lecture 5에서 다룰 것이다. 이 외에도 파노라마 카메라, 이벤트 카메라 등의 특별한 카메라 타입이 사용되기도 한다. 여러분은 우리가 Little Carrot의 머리에 박아준 카메라가 바로 양안 카메라임을 눈치챘을 것이다. 그럼 각 카메라 타입의 장단점을 살펴보자.

monocular (단안) 카메라

• 하나의 카메라만을 사용하는 SLAM 시스템을 monocular SLAM이라고 부른다. 적용이 단순하고, 또 저렴하기 때문에 자주 선택되는 옵션이다. 단안 카메라의 아웃풋 데이터는 한장의 사진이다. 이것으로 무엇을 할 수 있을까?
• 사진은 본질적으로 장면을 카메라의 이미지 평면에 투사한 projection이다. 사진을 찍는다는 것은 3차원의 세계를 2차원의 형태로 투영하는 것인데, 이 투영 과정에서 한 차원의 소실이 일어난다. 이때 잃어버리는 1차원은 depth(또는 distance) 정보를 담고 있는 차원이다.
• 따라서 단안 케이스에서 우리는 장면 내 물체와 카메라 사이의 거리값을 알 수 없는데, 뒤에서 보겠지만 이 거리값은 SLAM에서 매우 중요한 정보이다. 사람의 경우 내재된 사전 지식- 물체의 예상 크기 등-을 통해 보통 이미지 내에 있는 여러 물체 간의 거리 관계 파악이 가능하다. 하지만 아래 그림과 같은 특정 경우에서는 사람도 객체의 거리와 크기를 특정할 수 없다. 아래 사진에 보이는 작은 사람들이 멀리 떨어져 있는 큰 물체(인간)인지, 가까이 있는 작은 물체(장난감)인지는 보는 각도를 바꿔 3차원 구조에 대한 추가적인 정보를 더 얻기 전에는 알 수 없다.
  
• 단안 카메라를 통해 얻은 이미지는 3D 공간에 대한 2D projection 이기 때문에 3D 구조를 복원하고자 한다면 우리는 카메라의 view angle을 바꿔야한다. monocular SLAM은 이 원리를 사용한다. 카메라를 움직이고, 그 움직임을 추정하고, 그러면서 장면 내 객체의 거리와 크기-즉, 장면의 구조-를 파악하는 것이다. 그렇다면 움직임과 구조를 어떻게 추정할 수 있을까?
• 우리는 일상 속의 관찰을 통해 그 방법을 이미 알고있다. 카메라를 오른쪽으로 이동하면, 이미지 내의 객체는 왼쪽으로 이동한다. 카메라에서 가까운 물체는 카메라의 움직임에 따라 이미지 내에서 빠르게 이동하고, 먼 물체는 느리게 이동한다. 따라서, 카메라가 움직일 때 이미지 내의 물체들의 이동은 픽셀 시차(pixel disparity)를 형성한다. 이 시차를 측정함으로써, 우리는 어느 물체가 가깝고 먼지를 정량적으로 결정할 수 있게 된다. 하지만 만약 우리가 어떤 물체가 가깝고 먼지 안다고 해도 그 크기는 상대적인 값에 머무른다. 예를 들어 우리가 영화를 볼 때, 영화의 한 장면에서 어떤 물체가 다른 물체보다 크다고는 말할 수 있지만 그 물체의 실제 사이즈를 정확히 알 수는 없다. 직관적으로 생각해보면, 만약 카메라의 움직임과 장면의 크기를 동시에 두 배씩 키워도 단안 카메라는 똑같은 이미지를 찍을 것이다. 이는 monocular SLAM을 통해 추정한 경로(trajectory)와 맵은 실제 경로 또는 맵과 알려지지 않은 인수배의 차이가 있음을 의미하고, 우리는 이 인수를 스케일이라고 부른다. monocular SLAM은 이미지만을 통해서는 실제 스케일을 결정할 수 없으므로 이런 특성을 스케일 모호성(scale ambiguity) 이라고도 부른다.

• 정리하자면, monocular SLAM에서 depth값은 병진 운동(translational movement)을 통해서만 계산될 수 있고, 실제 스케일은 결정할 수 없다. 이 두가지 특성으로 인해 monocular SLAM의 실제 적용은 많은 문제가 생기기도 한다. 근본적인 원인은 하나의 이미지로는 depth를 결정할 수 없다는 것인데, 그래서 실제 스케일에 맞는 depth를 얻기 위해 우리는 stereo나 RGB-D 카메라를 쓰기 시작했다.

Stereo (양안) 카메라와 RGB-D 카메라

• 거리값을 알고 나면 단일 프레임으로부터 장면의 3D 구조를 복원하는 게 가능해지고, 스케일 모호성 또한 없어진다. Stereo와 RGB-D는 각각 다른 원리를 사용하여 실제 거리값을 계산한다.
• 스테레오 카메라는 두 개의 동기화 된 단안 카메라로 이루어져있다. 두 카메라 간의 물리적인 거리- 베이스라인(baseline) 이라고 부름-가 실제 값으로 주어지고, 이를 이용해 우리는 실제 사람의 눈과 매우 비슷한 원리로 각 픽셀의 3D 위치를 계산할 수 있다. 우리 인간은 왼쪽 눈과 오른쪽 눈으로 들어오는 이미지 간의 차이를 이용해 물체의 거리를 추정하는데, 같은 방식으로 아래 그림과 같이 각 픽셀의 거리값을 계산한다. 다만, 이 연산을 컴퓨터로 구현하면 꽤나 큰 연산량을 필요로 한다. 이러한 방식은 스테레오 뿐 아니라 multi-camera 시스템으로도 확장될 수 있지만 여러 대의 카메라로부터 구하는 결과라고 훨씬 정확하다거나 하지는 않다.
  
• 스테레오 카메라가 측정 할 수 있는 depth 범위는 베이스라인 길이와 관련이 있다. 베이스라인이 길면 더 멀리까지 측정할 수 있다. 따라서 보통 자율주행 기기에 부착되는 스테레오 카메라는 꽤 긴 베이스라인을 갖고있다.
• 스테레오 카메라의 단점은 configuration과 calibration 과정이 복잡하다는 것이다. 이들의 depth 범위와 정확도는 베이스라인 길이와 카메라 해상도(resolution)에 따라 제한된다. 또한, 앞서 말했듯이 스테레오 매칭과 시차 계산 과정은 많은 계산량을 필요로 하고 보통 GPU나 FPGA같은 가속기가 있어야 실시간 연산을 소화할 수 있다. 따라서 대부분의 스테레오 SOTA 알고리즘에서조차 계산비용이 여전히 주요 문제 점 중 하나로 남아있다.
• depth 카메라 (RGB-D 카메라)는 2010년 이후 부상한 새로운 카메라 타입이다. 레이저 스캐너와 비슷하게, RGB-D 카메라는 적외선이나 ToF(Time-of-Flight) 원리를 사용하여 물체에 빛을 쏘고 반사되는 빛을 수신하여 물체와 카메라 사이의 거리를 측정한다. 양안 카메라가 소프트웨어적인 해결법을 사용한다면, RGB-D 카메라는 물리적인 센서를 활용함으로써 계산 자원을 매우 절감하였다. 일반적으로 많이 쓰이는 RGB-D 카메라는 Kinect / Kinect V2, Xtion Pro Live, RealSense 등등이 있다. 하지만, RGB-D 카메라도 작은 FOV(field of view), 작은 depth 측정 범위, 데이터의 노이즈, 태양광 간섭에 민감하며 투명한 물체를 측정할 수 없다는 점 등 여러 이슈를 가지고 있다. SLAM에의 활용에 있어 RGB-D 카메라는 보통 실내환경에서 쓰이고 실외환경에는 적합하지 않다고 여겨진다.
  

이렇게 일반적인 카메라 타입들을 간단히 살펴보았다. 이제, 장면에서 움직이고 있는 카메라를 상상해보라. 우리는 카메라로부터 연속적으로 변화하는 일련의 이미지들을 얻을 것이다. Visual SLAM의 목표는 이 이미지들을 이용해 localization과 building map을 수행하는 것이다. 이건 꽤 복잡한 작업이기 때문에 하나의 알고리즘만으로 이미지를 입력받아 위치와 맵에 대한 정보를 연속적으로 출력하도록 만드는 것은 불가능하다. SLAM은 여러 알고리즘을 통합한 프레임워크를 통해 수행되는데, 수십년에 걸친 연구 끝에 아래와 같은 정형화된 형태가 확립되었다.

1.2 기본적인 Visual SLAM 프레임워크

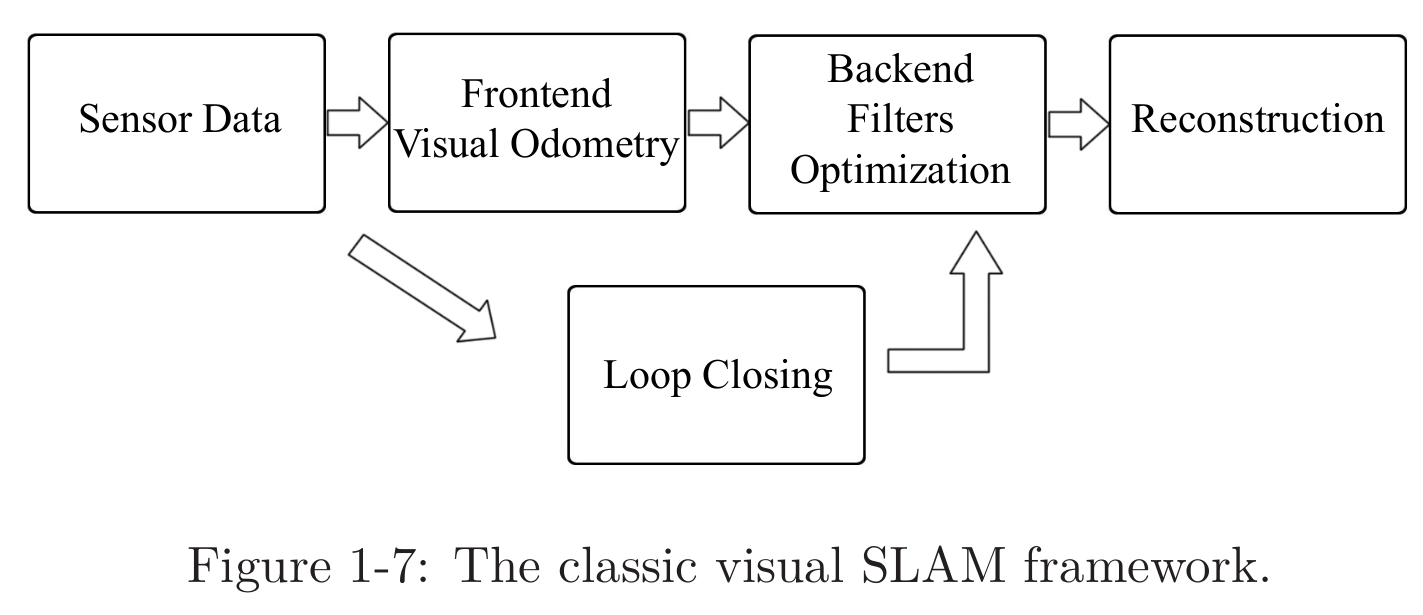
1. 센서 데이터 취득
   : Visual SLAM에서는 주로 카메라 이미지를 취득하고 전처리하는 과정을 일컫는다. 이동형 로봇의 경우 모터 인코더나 IMU 센서 등의 취득/동기화 또한 포함될 수 있다.
2. Visual Odometry (VO)
   : VO의 과제는 인접 프레임간 카메라의 움직임(ego-motion)을 추정하고 대략적인 부분 맵(local map)을 생성하는 것이다. VO는 프론트엔드라는 용어로 표현되기도 한다.
3. 백엔드 필터링/최적화
   : 백엔드는 VO로부터 각각의 time stamp에서의 카메라 포즈를 전달받고 루프 클로징의 결과를 전달받아 최적화를 적용하여 전체적으로 최적화된 경로와 맵을 만들어준다. VO 다음에 연결되기 때문에 백엔드로 불린다.
4. 루프 클로징
   : 루프 클로징은 로봇이 이전의 위치로 되돌아왔는지 여부를 알아내는 부분이다. 이를 탐지하면 축적되는 드리프트 에러 (drift error)를 감소시킬 수 있다. 만약 루프가 감지되면, 이 정보를 백엔드로 전달해 최적화에 활용할 수 있도록 한다.
5. 환경 재건(reconstruction)
   : 추정된 카메라의 trajectory를 바탕으로 task-specific한 맵을 구성한다.

위 프레임워크는 몇십 년간의 시행착오 끝에 정착된 것으로, 사실 안정적인 조명 조건과 제한되고 고정된 환경과 사람의 특별한 방해가 없는 경우를 상정한다면 visual SLAM 문제는 이미 해결되었다고 봐도 된다. (문제는 현실에서는 이런 가정이 통하지 않는다는 것😂)

이제 각 모듈의 기능에 대해 자세히 알아볼 건데, 작동 원리를 더 깊이 이해하려면 여러 수학적 지식이 추가로 필요하며 이는 책의 part 2에서 자세히 다룰 것이다. 지금은 각 모듈에 대한 직관적이고 정성적인 이해에 집중해보자.

Visual Odometry (VO)

VO는 인접 이미지 프레임 사이의 카메라 움직임을 파악하는 작업으로 가장 간단한 경우로는 앞뒤 연속 이미지 사이의 움직임을 추정하는 일이 될 것이다. 아래 두 이미지를 보면 우리는 자연히 오른쪽 이미지를 왼쪽으로 살짝 회전하면 왼쪽의 이미지가 될 것이라는 것을 알아챌 수 있다 (비디오로 보았으면 좀 더 쉬웠을 것이다). 이때 여러분은 '왼쪽으로 살짝 돌린다'는 움직임을 어떻게 두 이미지를 통해 알아챘는가?
아마 자연스럽게 이런 생각을 했을 것이다. “보자, 바테이블은 지금 가깝고 벽이랑 블랙보드는 멀리 떨어져있지. 카메라가 왼쪽으로 돌면 바테이블의 가까운 부분이 나타나기 시작할거고, 오른쪽의 캐비닛은 이미지 밖으로 나가기 시작하겠지?” 이 정보들로 우리는 카메라가 왼쪽으로 돈다고 결론짓게 된다.

여기서 더 나아가서, 여러분은 카메라가 얼만큼 돌았는지 또는 이동했는지 각도나 센티미터 단위로 대답 할 수 있는가? 이는 인간에게도 어려운 문제이다. 왜냐하면 우리 직관은 숫자에는 약하기 때문이다. 하지만 컴퓨터에게는, 이런 움직임은 숫자로 설명되어야한다. 그렇다면 어떻게 컴퓨터가 이미지들만으로 카메라의 움직임을 계산하게 할 수 있을까? Visual SLAM에서 주어지는 것은 이미지 내 픽셀들의 값과 그들이 공간의 한 점을 카메라의 이미지 평면으로 투영한 결과라는 사실 뿐이다. 카메라의 움직임을 정량화하기 위해서는 첫째로 카메라와 공간상의 점들 간의 기하학적 관계를 이해해야 한다. 이 관계를 밝히기 위해서는 약간의 배경지식이 필요하지만, 여기서는 우선 직관적인 개념만을 이해해도 충분하다. 현재로서는 VO가 인접 프레임의 이미지들로부터 카메라 움직임을 추정하고 장면의 3D 구조를 복원할 수 있다는 내용만 가져가면 된다. 이름에 odometry가 들어가는 이유는, VO가 실제 휠 오도메트리 (휠 인코더를 이용한)와 유사하게 순간순간의 ego-motion만 계산하고 글로벌 맵이나 절대 포즈 (absolute pose)를 추정하지 않기 때문이다. VO는 금붕어같이 금방금방 까먹고 전체적인 구조정보를 사용하지 않는다.

이제 우리가 VO를 구현을 해놔서, 지금 모든 앞뒤 프레임 간 카메라 움직임을 추정할 수 있다고 가정해보자. 만약 우리가 인접한 움직임끼리 모두 연결한다면 이는 자연히 로봇의 전체 경로를 나타내게 될 것이고 그럼 localization 문제는 끝이다. 또, 우리는 각 시간의 카메라 위치에서의 모든 픽셀들의 3D 위치를 계산할 수 있게 되고, 이것을 통합하면 맵을 형성할 수 있다. 여기까지 보면 VO만으로 SLAM 문제가 거의 해결된 것 처럼 보인다. 정말 그럴까? VO는 visual SLAM 문제를 풀기 위한 핵심 기술이 맞다. 우리는 이 책에서 VO에 대한 자세한 설명을 제공하기 위해 꽤 많은 부분을 투자할 것이다. 하지만, VO 만을 사용해 경로를 추정하는 것은 필연적으로 드리프트의 축적을 수반한다. 각 추정에는 항상 일정 오차가 따라온다. odometry가 작동하는 방식 때문에 이전 순간의 오차는 다음 순간으로 그대로 전파되고, 일정 시간이 지나면 추정이 부정확해지게 된다. 예를 들어, 로봇이 처음에 왼쪽으로 90도 돌고 그 다음 오른쪽으로 90도 돌았다고 해보자. 오차로 인해 우리는 처음 90도의 회전을 89도로 추정했다. 그러면 로봇이 다시 오른쪽으로 회전했을 때 로봇의 추정된 위치가 원점이 아니라는 사실이 우리를 당황스럽게 만들 것이다. 더 기분 나쁜 사실은, 이후의 모든 추정이 완벽하게 정확하게 이루어져도 이 처음의 1도 실수는 지워지지 않고 모든 경로상에 반영될 것이라는 점이다!

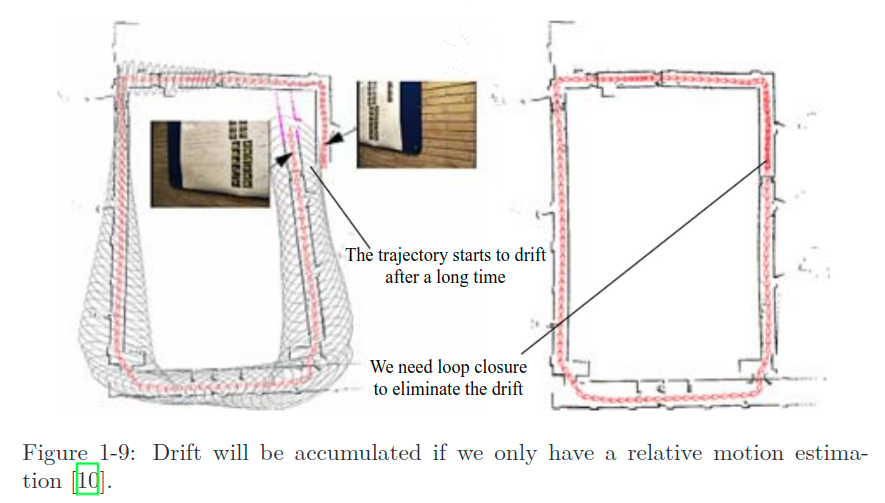
축적되는 드리프트는 일관성있는 맵을 구축할 수 없도록 만든다. 일자 복도는 비스듬해지고, 직각 코너는 비뚤어지게 된다🤮
드리프트 문제를 해결하기 위해 우리는 두가지 요소가 추가로 필요한데, 바로 뒤에 나오는 백엔드 최적화와 루프 클로징이다. 루프 클로징은 로봇이 이전 위치로 돌아왔는지를 판별해주고, 백엔드 최적화는 이런 정보들을 바탕으로 전체 경로의 모양을 교정해주는 역할을 한다.

백엔드 최적화

제너럴하게 말하자면, 백엔드 최적화는 SLAM 시스템에서 노이즈를 처리하는 부분을 맡고 있다고 할 수 있다.
모든 센서 데이터가 정확하면 정말 좋겠지만, 실제로는 가장 비싼 센서조차도 일정량의 노이즈를 항상 포함한다. 거기에 더해 많은 센서의 성능은 주변의 자기장이나 온도 등에 많은 영향을 받는다. 따라서 이미지로부터 카메라의 움직임을 추정하는 문제를 푸는것에 더해 우리는 이 추정이 어느정도의 노이즈를 포함하고 있는지, 이전 시간으로부터 다음 시간까지 이 노이즈가 어떻게 전파되어오는지, 현재 추정치를 어느정도 신뢰할 수 있는지를 추가적으로 고려해야한다. 백엔드 최적화는 노이즈를 포함한 인풋 데이터로부터 전체 시스템의 상태(state)를 추정하고 그들의 불확실성(uncertainty)을 계산한다. 여기서 말하는 상태는 로봇 자체의 경로와 환경에 대한 맵 둘 모두를 포함하는 개념이다.

SLAM 프레임워크에서 프론트엔드는 백엔드에 최적화할 데이터와 그 초기값을 전달한다. 백엔드는 넘겨받은 데이터의 최적화만을 진행하기 때문에, 이미지랑은 이제 관계가 없고 전달받은 숫자와 행렬들과만 관련이 있다. 따라서 visual SLAM에서 프론트엔드는 컴퓨터 비전의 영역과 맞닿아 있고- feature 추출과 매칭 등- 백엔드는 상태 추정 이론(state estimation theory)과 밀접한 관련이 있다고 할 수 있다. 역사적으로 오랫동안 백엔드의 최적화 파트 자체가 SLAM 연구의 동의어였다. 초기 SLAM 문제는 지금의 백엔드가 해결하려고 하는 것과 정확히 일치하는, 상태 추정에 대한 문제 그 자체로 설명되었다. 초기 논문에서 이는 “estimation of spatial uncertainty”로 명명되었으며, 이는 SLAM의 근본적인 특성- 자기 자신의 움직임과 주변 환경에 대한 uncertainty를 추정하는-을 직접적으로 설명하는 용어였다. 우리는 상태 추정 이론을 이용해 상태에 대한 mean과 covariance(=uncertainty)를 추정하기 위해 다양한 필터나 비선형 최적화 등을 사용한다. 자세한 이론적 내용은 5장, 8장 및 9장에서 설명한다.

루프 클로징

loop closure detection으로도 알려진 루프 클로징 모듈은 주로 SLAM에서의 위치 추정에서 발생하는 드리프트 에러를 해결하는 역할을 한다. 로봇이 일정 시간 이동 후 원점으로 돌아왔다고 가정했을 때, 실제로 우리가 추정하는 마지막 위치는 드리프트로 인해 원점이 아닐 것이다. 이 오차를 어떻게 교정해줄 수 있을까? 만약 로봇에게 그것이 사실은 현재 원점으로 돌아왔다는 것을 알려줄 방법이 있다면, 우리는 현재 위치를 원점으로 끌어다 놓음으로써 드리프트를 제거할 수 있을 것이다. 이게 정확히 루프 클로징이 하는 일이다.

루프 클로징은 localization과 map building 둘 모두와 깊은 관계가 있다. 사실, 맵을 구축하는 주된 목적 중 하나가 로봇이 자신이 다녀온 장소를 알 수 있도록 하는 것이기도 하다. 루프 클로징을 가능케 하기 위해선 로봇이 이전에 방문한 장면을 식별할 수 있도록 해주어야 하는데, 예를 들자면 로봇이 출발하는 곳에 QR 코드와 같은 마커를 설치하는 식의 방법을 생각해 볼 수 있다. 만약 동일한 마커를 다시 목격한다면 우리는 로봇이 원점으로 돌아왔다는 것을 알 수 있다. 하지만 마커는 앞서 말했듯이 침입형 센서이다. 비침입형 센서만으로 로봇이 루프 클로징을 수행하려면 어떻게 해야 할까? 가능한 방법 중 하나는 이미지 간의 유사도를 측정하는 것이다. 사람은 비슷한 두 이미지를 보고 두 이미지가 같은 장소에서 찍힌 것인지 아닌지 쉽게 판별할 수 있다. 따라서 우리가 살펴볼 시각적 루프 탐지는 이미지 간 유사도를 측정하는 알고리즘이라고 봐도 된다.

루프가 탐지되고 나면, 우리는 백엔드 최적화 알고리즘에게 “자, A랑 B는 같은 점이야!”와 같은 정보를 전달하게 된다. 이 정보를 바탕으로 전체 경로와 맵은 A와 B를 한 점으로 잇도록 조정될 것이다. 이런 방식을 통해, 충분하고 신뢰할 수 있는 루프 탐지를 가지고 있다면 축적된 에러를 제거하고 전체적으로 일관성있는 경로와 맵을 얻을 수 있게 된다.

매핑

매핑은 맵을 구축하는 과정을 뜻하는데, 맵이라는건 아래 그림과 같이 환경에 대한 묘사를 의미하고 이 묘사는 정해져 있는 것이 아니라 실제 용도에 따라 어떤 형태든 될 수 있다.

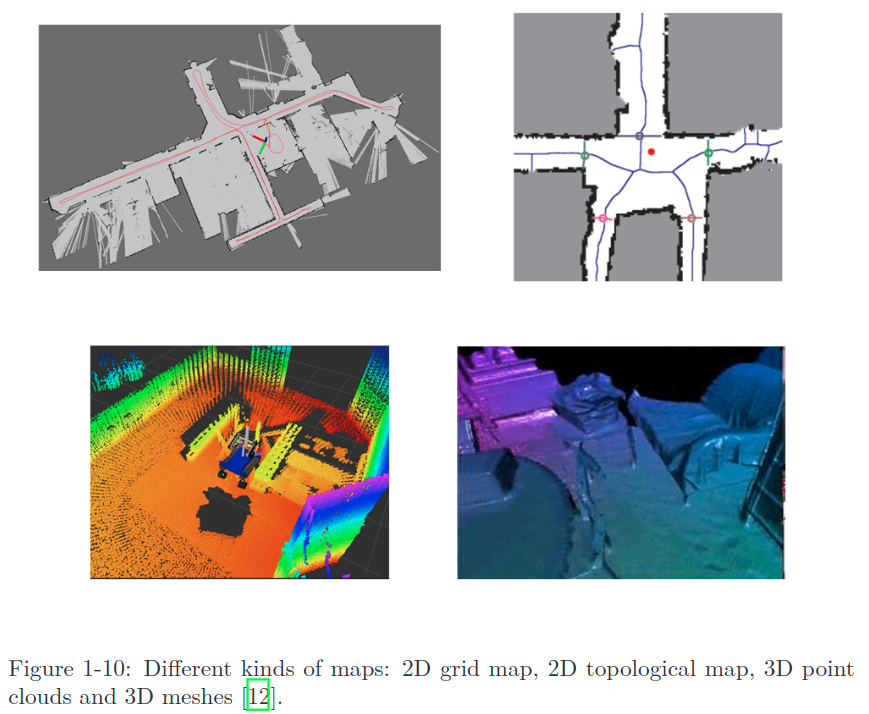
로봇 청소기를 예로 들어보자. 로봇 청소기는 바닥에 붙어서 움직이기 때문에 네비게이션을 위해서는 single-line 레이저 스캐너를 이용해 만든 2D 맵이면 충분할 것이다. 카메라의 경우에는 카메라의 6-DoF(degree-of-freedom) 움직임을 커버할 수 있는 최소 3차원의 맵이 필요할 것이다. 가끔 우리는 단순한 점들의 집합이 아닌 부드럽고 아름다운 삼각면의 텍스쳐들로 이루어진 모델링 결과가 필요할 수도 있다. 또는, 생김새는 전혀 신경쓰지 않고 “점 A와 점 B는 연결되어있고, 점 B와 점 C는 연결되어있지 않군” 과 같은 위상적인(topological) 정보만을 필요로 할 수도 있다. 아니면 가끔은 맵 자체가 아예 필요하지 않을 수도 있다. 예를 들어 level 2 자율주행차는 차선에 상대적인 움직임만을 추정함으로써 차선을 따르며 주행할 수 있다. 이렇게 맵에 대한 요구조건이나 아이디어는 용도에 따라 다양한 모습을 띤다. 앞서 말한 VO나 루프 탐지, 백엔드 최적화와는 다르게 매핑은 특정 알고리즘을 가지고 있지 않다. 여러 형태가 될 수 있는 이 맵이라는 개념은 크게는 두가지 카테고리로 나뉜다.

• Metric Map
  • Metrical map은 물체의 정확한 미터법상 위치를 강조한다. 보통 sparse하냐 dense하냐로 분류되기도 한다. sparse metric map은 장면을 모든 물체를 나타내지 않고 간결한 형태로 나타내어 저장한다. 예를 들자면 도로환경에서 차선이나 교통신호 등의 대표적인 랜드마크들만을 선택하여 sparse map을 구성할 수 있다. 반대로 dense metrical map은 보이는 모든 것을 모델링하는데 초점을 맞춘다. sparse map은 localization에는 충분할 수 있지만 navigation을 위해서는 보통 dense map이 필요하다 (그렇지 않다면 우리는 아마 두 랜드마크 사이의 벽에 콰당 부딪힐 수도 있을 것이다). dense map은 보통 특정 해상도의 작은 격자들로 구성된다. 예를 들자면 2D의 경우 occupancy grid의 형태를 사용 할 수 있고, 3D의 경우 voxel grid를 사용 할 수 있다.
  • 이 맵은 A*, D*와 같은 다양한 navigation 알고리즘에 사용될 수 있다. 하지만 공간 크기를 모두 커버하는 격자 구조에 모든 상태를 저장하는 이런 방식은 저장공간을 많이 잡아먹는다. 이외에도 다른 여러 이슈들이 존재한다. 예를 들어 큰 규모의 metrical map에서 매핑 시의 작은 에러가 두 방 사이의 벽이 겹쳐져버리도록 만들 수도 있다.
• Topological Maps
  • metric map과 비교했을 때, topological map은 맵 요소 간의 관계에 조금 더 집중한다. topological map은 노드와 엣지로 이루어진 그래프 구조이며, 각 노드 간의 연결성만을 고려한다. 예를 들자면 실제로 점 A와 점 B가 얼마나 떨어져있는지는 궁금하지 않고 두 점이 연결되어있는지 여부만이 중요한 상황이 있을 수 있다. 이는 정확한 위치를 구축하는 것에 대한 부담을 덜어주고, 맵에서 디테일을 제거함으로써 좀더 콤팩트한 표현을 가능하게 한다.
  • 하지만 이런 topological map은 복잡한 구조를 나타내기엔 좋지 않다. 또한 노드와 엣지를 형성하기 위해 맵을 쪼개는 방법과 navigation/path planning을 위해 topological map을 어떻게 활용할지에 대한 질문은 여전히 답이 정해지지 않은 문제이다.

1.3 SLAM 문제를 수학적 표현을 사용해 나타내보자

Little Carrot이 몇가지 센서를 장착하고 미지의 환경에서 돌아다니는 상황을 수학적인 언어로는 어떻게 나타낼 수 있을까? 우선 센서들은 개별 time point에서 데이터들을 모으기 때문에, 우리는 그 순간순간의 맵과 위치만을 고려한다. 즉, 움직임이라는 연속적인 과정을 우리는 데이터 샘플링이 일어나는 불연속적인 time step ($1,...,k$) 상에서 해석한다는 말이다. $\textbf{x}$를 사용해 Little Carrot의 위치를 나타낸다면, 각 time step에서의 위치는 $\textbf{x}_1$,..., $\textbf{x}_k$와 같이 표현될 수 있을 것이고, 이들은 Little Carrot의 경로를 이루게 된다.
맵의 경우엔, 우리는 맵이 몇 개의 랜드마크들로 구성되어있다고 가정한다. 각 time step에서 센서들은 랜드마크들의 일부를 볼 수 있고, 그 관찰(observation)을 기록한다. $\textbf{y}_1$,..., $\textbf{y}_N$를 사용해 맵 상 존재하는 총 N개의 랜드마크를 표현하도록 하자.

이 설정 하에, 'Little Carrot이 몇가지 센서를 장착하고 미지의 환경에서 돌아다니는 상황'은 기본적으로 다음 두 부분으로 이루어져있다.
1. motion: time step $k-1$ -> $k$ 사이에 Little Carrot의 위치 $\textbf{x}$가 어떻게 변하는지
2. observation: Little Carrot이 위치 $\textbf{x}_k$에서 $\textbf{y}_j$라는 랜드마크를 탐지하는 상황

motion equation

로봇에게 "왼쪽으로 15도 돌아"와 같은 모션 명령을 전달하면 이 명령은 컨트롤러를 통해 여러 방식으로 수행된다. 우리는 로봇의 위치에 대한 명령을 내릴 수도 있고, 가속도나 각속도 등을 조종할 수도 있다. 어쨌든 이런 다양한 컨트롤의 종류에 관계 없이 우리는 다음의 보편적이고 추상적인 수학 모델을 이용해 로봇의 모션을 나타낼 수 있다.

여기서 $\textbf{u}_k$는 인풋 명령을 의미하고, $\textbf{w}_k$는 노이즈를 의미한다. 여기서 우리는 특정 수식이 아닌 제너럴한 표현인 $f(\cdot)$를 사용해 프로세스를 표현함으로써 어떤 모션 인풋이든 나타낼 수 있도록 하였다. 이 수식을 motion equation이라고 한다.
노이즈의 존재는 이 모델을 확률 모델(stochastic model)로 바꾼다. 즉, 우리가 “앞으로 1미터 직진”이라는 명령을 한다고 해도 그게 로봇이 실제로 정확히 1미터 갈 거라는걸 의미하진 않는다. 만약 모든 지시가 정확하게 수행된다면 사실 추정 작업 자체가 필요가 없지만, 로봇이 언제는 0.9미터를 가고 언제는 또 1.1미터를 가는게 현실이다. 따라서 각 움직임에서 노이즈는 랜덤하게 적용된다. 만일 우리가 노이즈를 무시한다면, 인풋 명령들로만 추정한 포지션은 불과 몇 분 뒤 실제 위치와 몇백 마일 떨어지게 될 수도 있다.

observation equation

motion equation과 비슷하게 observation equation이라는 것이 있는데, 이 수식은 Little carrot이 위치 $\textbf{x}_k$에서 랜드마크 $\textbf{y}_j$를 보고 관측 데이터 $\textbf{z}_{k,j}$를 생성하는 상황을 묘사한다. 이 관계 또한 일반성을 잃지 않도록 추상적인 함수 $h(\cdot)$를 이용해 표현해보자.

여기서 $\textbf{v}_{k,j}$는 observation의 노이즈이다. 여러 센서 종류에 따라 관측 데이터 $\textbf{z}$와 observation eq. $h$는 다양한 형태가 될 수 있다.

여러분은 아마 "아니, 그래서 $f$, $h$는 정확히 뭐고 $\textbf{x}$, $\textbf{y}$, $\textbf{z}$는 뭘 나타내는거야.."라며 모호한 표현에 혼란을 느끼고 있을 지 모른다.
실제 적용에서는 모션이나 센서의 종류에 따라 몇가지 종류의 특정한 매개변수화(parameterization) 방법이 존재한다. 매개변수화란 다음과 같은 것이다. 로봇이 평면 상에서 움직인다고 할 때 로봇의 포즈는 2차원의 $x-y$ 좌표와 각도로 표현될 수 있다. 즉, 이 상황에서 로봇의 포즈 $\textbf{x}_k$는 두 축 상에서의 위치 $x_1$, $x_2$와 각도 $\theta$를 통해 $\textbf{x}_k = [x_1, x_2, \theta]^T_k$와 같이 나타내어질 수 있다. 이 때, 인풋 명령은 단위시간 사이에서 이 위치와 각도의 변화량($\triangle$)으로 해석될 수 있으므로, $\textbf{u}_k=[\triangle x_1, \triangle x_2, \triangle \theta ]^T_k$와 같은 형태로 표현해보자. 그러면 motion equation은 다음과 같이 매개변수화된다.

여기서 $\textbf{w}_k$는 앞에서 말했듯이 노이즈이다. 위 식은 간단한 선형관계를 나타낸다. 하지만 모든 인풋 명령이 이런식으로 위치와 각도의 변화량으로만 구성되어있진 않다. 예를 들어, 스로틀이나 조이스틱의 인풋은 속도나 가속도이므로 위와는 다른 형태의 조금 더 복잡한 motion equation을 갖게 된다. 그 때는 역학에 대한 추가적인 지식이 필요하다.

observation equation의 경우에는 예를 들어 로봇이 2차원의 레이저 센서를 사용한다고 해보자. 레이저는 로봇과 랜드마크 사이의 거리 $r$과 각도 $\phi$를 측정함으로써 2D 랜드마크를 관측한다. 랜드마크가 $\textbf{y}_j =[y_1,y_2]^T_j$에 있고, 로봇의 포즈가 $\textbf{x}_k=[x_1,x_2]^T_k$, 관측데이터를 $\textbf{z}_{k,j}=[r_{k,j}, \phi_{k,j}]^T$로 놓으면 observation eq.는 다음과 같이 표현된다:

visual SLAM으로 한정해 생각해보면, 센서는 카메라이고 observation eq.는 '랜드마크에 대한 이미지의 픽셀을 가져오는' 과정으로 생각해 볼 수 있다. 이는 카메라 모델에 대한 수식과 관련되어있고, chapter4에서 자세히 다뤄볼 것이다.

확실히 motion/observation 이 두 식은 센서 별로 매우 다른 형태로 매개변수화된다는 것을 알 수 있는데, 만약 우리가 범용성을 유지하면서 이들을 일반적인 abstract form으로 표현해본다면 SLAM 프로세스는 다음의 두 기본식으로 요약 가능하다.

여기서 $\mathcal{O}$는 랜드마크를 관측했던 위치에 대한 정보를 담고있는 집합(모든 순간에 랜드마크 관측이 가능하진 않다- 보통 한 순간에 랜드마크의 작은 일부만을 관측할 수 있음)이다. 이 두 식은 동시에 SLAM의 기본적인 문제를 묘사한다: “어떻게 노이즈가 포함된 인풋 컨트롤 $\textbf{u}$와 센서 관측값 $\textbf{z}$를 가지고 $\textbf{x}$(localization)와 $\textbf{y}$(mapping)를 정확하게 추정할 수 있을까?”
지금 보이듯이 우리는 SLAM 문제를 상태 추정 문제로 모델링하였는데, 그럼 어떻게 노이즈가 포함된 측정값들을 통해 내부적인(숨겨진) 상태 변수들을 추정할 수 있을까?
해법은 두 식의 특정한 형태와 noise의 확률분포에 있다. motion / observation eq. 가 선형이거나/비선형이거나, 노이즈가 gaussian/non-gaussian 으로 가정된다면, 모델은 선형/비선형, gaussian/non-gaussian 시스템으로 분류된다. 선형-가우시안(LG system) 은 가장 간단하고, 이것의 편향되지않은 최적의 추정치는 칼만 필터 (KF)를 통해 구할 수 있다. 복잡한 nonlinear non-gaussian(NLNG system)의 경우엔 기본적으로 extended Kaman filter (EKF), nonlinear optimization 두 가지 방법에 의존한다. 21세기 초반까지는 SLAM에서 EKF기반 방식이 지배적이었다. 이에 따라, EKF의 단점(부분 선형화에 따른 오차라든가 noise를 가우시안 분포로 추정하는 것 등)을 극복하기 위해 사람들은 입자 필터와 같은 다른 필터들을 사용하기 시작했고, 비선형 최적화 방법도 쓰기 시작했다. 오늘날 visual SLAM은 SOTA 최적화 방식인 그래프 최적화를 사용하는 것이 주류가 되었다. 현재로서는 최적화 방법이 명백하게 필터 기반 방식보다 우월하다고 생각되며, 컴퓨팅 파워가 받쳐주는 한 최적화 방법이 보통 선호된다(챕터8, 9).

여기까지 왔으면 SLAM의 수학적 모델에 대한 전반적인 이해는 되었으리라 생각하지만, 여전히 분명하게 해야 할 이슈 몇가지가 있다.
첫째로, 우리는 포즈 $\textbf{x}$가 무엇인지 엄밀하게 정의해야 한다. 포즈라는 단어는 조금 모호하다. 앞에서는 계속 2D의 예시를 들었지만 많은 로봇은 3차원의 공간 상에서 움직인다. 3차원 공간에서의 모션은 3개의 좌표축 상의 평행이동과 회전으로 표현되고, 이는 총 6개의 degree of freedom (DoF)을 가진다. 그럼 6차원의 벡터로 표현된다는건가 하면 그것보다는 살짝 더 복잡하다. 그럼 6DoF 포즈를 어떻게 표현해야 하고, 그걸 어떻게 최적화할 것인가? 이를 어떻게 수학적 성질을 이용해 표현할 것인가? 이 내용이 chapter 2,3에서 주요하게 다룰 내용이다.
다음으로, 우리는 visual SLAM에서 observation equation이 어떻게 매개변수화되는지를 다룰 것이다. 다른 말로, 어떤 과정을 통해 공간 상의 랜드마크 점이 사진에 투영되는지를 살펴볼 것이다. 이를 위해서는 카메라의 투영 모델과 왜곡에 대한 설명이 필요하며, 챕터 4에서 다룰 것이다. 마지막으로, 우리가 이 모든 정보를 알고있을 때 상태 추정 문제를 풀기 위해 필요한 비선형 최적화에 대한 지식을 챕터 5에서 다룰 것이다.
위의 내용이 이 책에서 수학적인 배경지식을 설명하는 부분인 파트1을 이루고, 나머지 파트에서는 visual odometry나 백엔드 최적화 등등에 대한 자세한 내용을 살펴본다.

1.4 실습: Basics

1.4.1 Ubuntu 설치하기

이런건 생략..

1.4.2 Hello SLAM

1.4.3 CMake 사용법 익히기

1.4.4 라이브러리 사용하기

리눅스에서 라이브러리 파일은 정적 라이브러리와 공유 라이브러리 두 개로 나뉜다.

정적 라이브러리는 “.a” 확장자를 가지고 있고, 공유 라이브러리는 “.so” 확장자를 가진다. 모든 라이브러리는 포장된 함수들의 콜렉션이다. 차이점은 정적 라이브러리는 그들이 불러질 때마다 카피를 생성하고, 공유 라이브러리는 하나의 카피만을 만든다는 것이다. 만약 정적 라이브러리 대신 공유 라이브러리를 생성하고싶으면 CMakeLists.txt에서 add_library를 할 때 SHARED 플래그를 추가해주면 된다.

1.4.5 IDE 사용하기

IDE란 Integrated Development Environments의 약어로, 파이참이나 VS Code 등의 개발을 도와주는 툴을 말한다. 기본적인 text editor만 있어도 코딩은 가능하지만 각종 자동완성부터 시작해 디버깅까지 다양한 지원기능을 활용하며 효율적인 개발을 하기 위해서는 개발에 없으면 안되는 존재인데, 이 세상에는 굉장히 다양한 IDE가 존재한다. 이 책에서는 KDevelop, CLion을 추천하는데 사실 나는 처음 들어보는 IDE이고, 개인적으로는 그냥 VSCode 쓰는 것을 추천한다. Extension이 넘치기 때문에 저자들이 말하는 KDevelop, CLion의 특장점을 커버하고도 남을거라 생각한다.