Introduction to Visual SLAM From Theory to Practice (2)

yeonsoo·2022년 11월 29일
MathematicsRoboticsSLAMTheory
1

Introduction to Visual SLAM

목록 보기
3/3

아래는 Xiang Gao와 Tao Zhang의 <Introduction to Visual SLAM>을 읽고 번역정리+추가적인 코멘트를 단 내용이다.
문장은 가능하면 간소화하고, 이론적으로 더 참고할만한 부분은 추가적인 코멘트를 넣었음.
저자에 의해 모든 자료가 무료 배포되었음. 아래 링크 참고
📘 영어판 도서 파일: https://github.com/gaoxiang12/slambook-en
📂 practice 코드: https://github.com/gaoxiang12/slambook2

2장. 3D rigid Body Motion

🔎 학습 목표
1. 3D 공간 상의 rigid body 기하학- 회전행렬, 변환행렬, 쿼터니언, 오일러각- 을 익힌다.
2. Eigen 라이브러리의 행렬&기하 모듈 사용법을 익힌다.

지난 시간에 우리는 visual SLAM의 전반적인 프레임워크와 내용을 살펴보았다.
이번 강의에서는 visual SLAM의 가장 기초적인 이론을 다룬다. 바로 3D 공간에서 어떻게 강체의 움직임을 나타낼 것인지에 대한 내용이다.
(계속 등장할 "강체" (rigid body)는 단순히 찌그러지거나 늘어나지 않는 단단한 덩어리의 개념이라고 생각하면 됨, 즉 움직임이나 외력에 의해 물체의 형태가 변하지 않는다는 가정을 담아 "물체"보다 좀 더 specific한 표현을 사용)

이 움직임은 회전과 평행이동의 조합으로 표현될 수 있다는 것은 직관적으로 느낌이 올 텐데, 평행이동 쪽은 상당히 간단하지만 회전 쪽은 생각보다 복잡한 문제들이 얽혀있다. 회전행렬과 쿼터니언, 오일러각의 의미와 그들이 어떻게 계산되고 변환되는지를 살펴보며 회전에 대한 개념을 정확히 잡아보도록 하자.
실습 파트에서는 Eigen이라는 가장 흔히 쓰이는 선형대수 라이브러리를 소개한다. Eigen은 C++ 행렬연산을 제공하고, 그 안의 기하학 모듈은 쿼터니언과 같은 기본적인 데이터 구조나 연산을 지원한다. Eigen은 고도로 최적화 되어있지만, 여전히 몇가지 이슈를 가지고 있다. 실습 파트에서 자세히 살펴보자!

2.1 회전행렬

2.1.1 점, 벡터, 좌표시스템

우리는 3차원 공간에서 살기 때문에 태생적으로 3D 움직임에 익숙하다. 3차원 공간은 3개의 축으로 이루어져있기 때문에 공간상의 한 점의 위치는 3개의 좌표로 특정 가능하다. 하지만 우리는 이제 한 점이 아닌, 위치(position)와 방향(orientation)을 가진 강체를 고려해야한다. 카메라 또한 3차원 공간상의 강체로 볼 수 있으므로 visual SLAM에서 우리가 구하려는 것 중 하나-카메라의 포즈- 역시 강체의 위치와 방향이 된다.
"현재 카메라의 위치는 (0,0,0)이고, 앞쪽을 보고 있어" 라는 말을 어떻게 수학적인 언어로 표현할 수 있을까?
가장 기본적인 개념인 점과 벡터에서부터 시작해보자.
길이와 부피가 없는 '점'은 공간의 가장 기본적인 성분이다. 두 점을 이으면 벡터가 된다. 벡터는 한 점에서 다른 한 점을 가리키는 화살표로 이해하면 된다. 여기서 잠깐 짚고 넘어갈 점은 벡터를 벡터 좌표와 혼동하면 안된다. 기본 선형대수 지식을 잠깐 떠올려본다면, 3D 공간 상 한 점의 좌표는 R3\mathbb{R}^3로 표현될 수 있다. 선형 공간에서 우리는 공간의 기저(base) 벡터 (e1,e2,e3)(\textbf{e}_1 , \textbf{e}_2, \textbf{e}_3)를 잡을 수 있다.

<기저벡터>
공간 상에서 선형 독립 (linearly independent)인 벡터의 집합
일반적으로 서로 orthogonal하고 단위길이를 가짐 (보통 계산하기 편하니까 그렇게 잡는다는거지 필수조건 아님)

그러고 나면, 임의의 벡터 a\textbf{a}는 이 기저벡터에 대한 좌표를 가지게 된다.

a=[e1,e2,e3][a1a2a3]=a1e1+a2e2+a3e3\textbf{a} = [\textbf{e}_1, \textbf{e}_2, \textbf{e}_3] \left[\begin{matrix} a_1 \\ a_2 \\ a_3 \end{matrix}\right] = a_1\textbf{e}_1 + a_2\textbf{e}_2 + a_3\textbf{e}_3

여기서 (a1,a2,a3)T(a_1, a_2, a_3)^T를 우리는 벡터 a\textbf{a}의 좌표라고 부른다.

즉 벡터의 좌표값은 벡터가 공간에 어떻게 뉘어져있는지 그 벡터 자체뿐만 아니라 기저벡터를 어떻게 잡냐에 따라 달라진다. R3\mathbb{R}^3에서 좌표 시스템은 일반적으로 3개의 orthogonal한 좌표축으로 이루어진다. 예를 들어 x,y\textbf{x}, \textbf{y} 축이 주어지면 z\textbf{z}축은 오른손의 법칙 또는 왼손의 법칙에 따라 x×y\textbf{x} \times \textbf{y}로 얻을 수 있다. 정의하기에 따라 좌표시스템은 왼손좌표계/오른손좌표계로 나뉘는데, 3번째 축은 두 시스템 간에 반대방향으로 정의된다. 대부분의 3D 라이브러리는 (OpenGL, 3DS Max 등..) 오른손좌표계를 사용하고, Unity나 Direct3D 등은 왼손좌표계를 사용한다.

여러분이 기본적인 선형 대수 지식은 있다고 가정하고 벡터나 스칼라 사이의 더하기-빼기와 같은 기본 연산에 관한 설명은 생략한다. 내적과 외적은 다시 한번 살펴본다.
두 벡터 a,b∈R3\textbf{a}, \textbf{b} \in \mathbb{R}^3 에 대해 내적은 다음과 같이 정의된다:

a⋅b=aTb=∑i=13aibi=∣a∣∣b∣cos⁡<a,b>\textbf{a} \cdot \textbf{b} = \textbf{a}^T\textbf{b} = \sum^{3}_{i=1}{a_ib_i} = |\textbf{a}||\textbf{b}|\cos\left<\textbf{a},\textbf{b}\right>

여기서 <a,b>\left<\textbf{a},\textbf{b}\right>는 두 벡터 간 각도를 의미한다. 내적은 두 벡터 간의 투영(projection) 관계를 나타내기도 한다.

외적의 경우:

a×b=∥e1e2e3a1a2a3b1b2b3∥=[a2b3−a3b2a3b1−a1b3a1b2−a2b1]=[0−a3a2a30−a1−a2a10]b≜a∧b\textbf{a} \times \textbf{b} = \Bigg\|\begin{matrix} \textbf{e}_1 & \textbf{e}_2 & \textbf{e}_3 \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{matrix} \Bigg\| = \left[\begin{matrix} a_2b_3 - a_3b_2\\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{matrix}\right]= \left[\begin{matrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{matrix}\right]\textbf{b} \triangleq \textbf{a}^\land \textbf{b}

두 벡터를 외적하면 결과는 두 벡터에 수직인 방향을 가지는 벡터가 된다. 길이는 ∣a∣∣bsin⁡<a,b>|\textbf{a}||\textbf{b}\sin\left<\textbf{a},\textbf{b}\right>이고, 이는 두 벡터가 이루는 사변형의 면적과 같다.
위의 ∧^\land라는 연산자는 벡터 a\textbf{a}를 skew-symmetric 행렬로 변환해주는 연산이다. 이를 이용하면 외적 a×b\textbf{a} \times \textbf{b}를 a∧b\textbf{a}^\land \textbf{b}라는 행렬과 벡터의 곱-선형 연산-으로 표현할 수 있다.
이 기호는 앞으로 자주 쓰일 것이니 기억해놓길 바란다. 이 연산은 일대일 매핑이라 임의의 벡터는 유일한 anti-symmetric 행렬을 가진다. (skew-symmetric, anti-symmetric 다 같은 말, 그냥 대각선을 기준으로 대칭인 성분끼리 부호 다르고 크기 같은 행렬을 뜻한다고만 알면 됨)

a∧=[0−a3a2a30−a1−a2a10]\textbf{a}^\land = \left[\begin{matrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{matrix}\right]

덧셈이나 뺄셈, 내/외적과 같은 모든 벡터 연산은 우리가 그들의 좌표를 모르더라도 (즉, 기저벡터를 특정해 벡터좌표를 구하지 않더라도) 계산될 수 있다는 것을 알아두라. 예를 들어 두 벡터의 좌표를 모르지만 내적을 하고 싶으면 두 벡터들의 길이와 각도를 통해 내적값을 계산할 수 있다. 내적 결과는 좌표시스템을 어떻게 선택하느냐와는 독립적이라는 뜻이다.

2.1.2 좌표계 간 유클리디안 변환

우리는 종종 하나의 환경에서 여러 좌표계를 정의한다- 로보틱스에서는, 매 링크와 관절마다 각각의 좌표계를 정의한다. 3D 매핑에서는, 각 cuboid나 cylinder마다 좌표계를 정의한다. 움직이는 로봇의 경우에는 고정 관성 좌표계(stationary inertial coordinate system, = 월드좌표계)를 사용하는 것이 일반적이다 (아래 그림의 xW,yW,zWx_W, y_W, z_W).

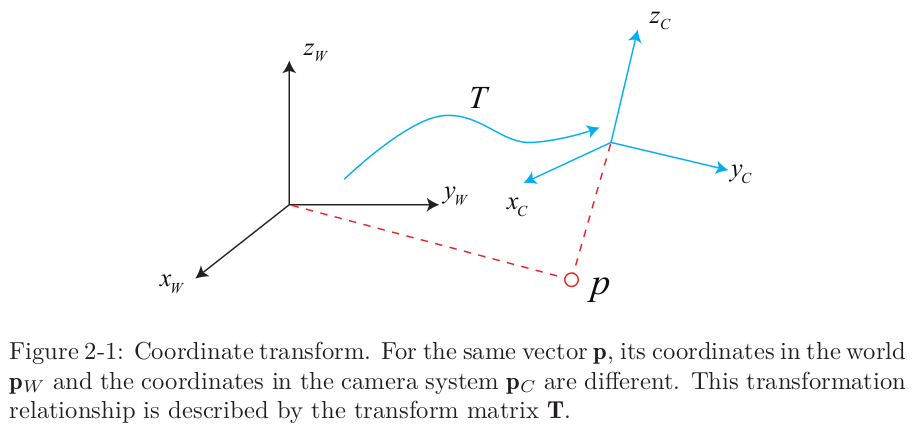
한편, 카메라나 로봇은 위 그림의 xC,yC,zCx_C, y_C, z_C에 해당하는, 움직이는 좌표계이다.

공간 상의 어떤 벡터 p\textbf{p}를 생각해보자. 이 벡터는 카메라 좌표계에서는 pc\textbf{p}_c라는 좌표를 가지고, 월드 좌표계에서 보면 pw\textbf{p}_w라는 좌표를 가지는데, 이 두 좌표 간 변환을 어떻게 해주면 될까? 우선은 카메라 좌표계 상에서의 좌표값을 구하고, 그 다음에 적절한 변환을 해주면 될 것 같은데, 이 변환과정을 수학적으로 표현해보자. 이제 설명하겠지만 이 과정은 변환행렬 T\textbf{T}로 표현이 가능하다.
직관적으로 생각해보면 위 그림의 두 좌표계는 하나를 조금 돌리고(회전) 평행이동 시키면 겹칠 수 있는데, 이 회전과 평행이동을 강체 운동 (rigid body motion)이라고 한다.
직관적으로, 두 좌표계 간의 motion은 rotation과 translation으로 이루어져있는데, 이를 rigid body motion이라고 한다. 당연히 카메라 모션도 강체운동이다. 강체운동에서는 벡터의 길이나 각도가 변하지 않는다. 공중으로 핸드폰을 던지는 경우를 생각해보라. 이 때는 공간적인 위치와 방향만이 바뀌고, 길이나 각 면의 각도 등은 바뀌지 않는다. 핸드폰이 모션 중에 지우개처럼 뭉개지거나 쭉 늘어나지는 않으니까! 이 상황에서 우리는 핸드폰의 움직임이 유클리디안이라고 말할 수 있다. (강체 변환과 유클리디안 변환은 동의어임)
반복해 말하지만 유클리디안 변환은 회전과 평행이동으로 이루어져있는데, 우선 회전을 살펴보자. 여기 단위길이의 orthogonal한 기저벡터 (e1,e2,e3)(\textbf{e}_1, \textbf{e}_2, \textbf{e}_3)가 있다. 회전 후에 이것들은 (e1′,e2′,e3′)(\textbf{e}'_1, \textbf{e}'_2, \textbf{e}'_3)가 된다. 그러면 공간 상에 그냥 가만히 누워있는 벡터 a\textbf{a}의 좌표는 [a1,a2,a3]T[a_1, a_2, a_3]^T 에서 [a1′,a2′,a3′]T[a'_1, a'_2, a'_3]^T로 바뀌게 되는데, 벡터 자체는 변하지 않았기 때문에 벡터 좌표의 정의에 따라 다음의 등식이 성립한다.

[e1,e2,e3][a1a2a3]=[e1′,e2′,e3′][a1′a2′a3′][\textbf{e}_1, \textbf{e}_2, \textbf{e}_3] \left[\begin{matrix} a_1 \\ a_2 \\ a_3 \end{matrix}\right] = [\textbf{e}'_1, \textbf{e}'_2, \textbf{e}'_3] \left[\begin{matrix} a'_1 \\ a'_2 \\ a'_3 \end{matrix}\right]

양쪽에 [e1Te2Te3T]\left[\begin{matrix} \textbf{e}^T_1 \\ \textbf{e}^T_2 \\ \textbf{e}^T_3 \end{matrix}\right] 를 곱하면 우변의 왼쪽 행렬이 단위행렬이 되면서 아래와 같은 식을 얻을 수 있다.

[a1a2a3]=[e1Te1e1Te2e1Te3e2Te1e2Te2e2Te3e3Te1e3Te2e3Te3]⏟rotation matrix[a1′a2′a3′]≜Ra′\left[\begin{matrix} a_1 \\ a_2 \\ a_3 \end{matrix}\right] = \underbrace{ \left[\begin{matrix} \textbf{e}^T_1\textbf{e}_1 & \textbf{e}^T_1\textbf{e}_2 & \textbf{e}^T_1\textbf{e}_3\\ \textbf{e}^T_2\textbf{e}_1 & \textbf{e}^T_2\textbf{e}_2 & \textbf{e}^T_2\textbf{e}_3\\ \textbf{e}^T_3\textbf{e}_1 & \textbf{e}^T_3\textbf{e}_2 & \textbf{e}^T_3\textbf{e}_3\\ \end{matrix}\right]}_{\text{rotation matrix}} \left[\begin{matrix} a'_1 \\ a'_2 \\ a'_3 \end{matrix}\right] \triangleq \textbf{R}\textbf{a}'

여기서 저 중간의 행렬을 행렬 R\textbf{R}로 정의한다. 이 행렬은 두 좌표계의 기저행렬들간의 내적으로 구성되어있으며, 회전 전후 동일 벡터의 좌표에 대한 변환관계를 담고있다. 같은 회전에 대해서는 어떤 벡터든 동일한 R\textbf{R}을 통해 변환할 수 있다. 이 행렬 R\textbf{R}를 회전행렬이라고 부르자.
한편, 행렬의 성분들은 두 좌표계간 기저행렬들의 내적으로 이루어진다. 기저행렬의 길이가 1이므로 이건 사실 기저행렬간 각도의 코사인을 취한 값과 동일하다. 따라서 이 행렬을 다른 말로 방향 코사인 행렬 (Direction Cosine Matrix, DCM)이라고 부르기도 하는데, 우리는 그냥 회전행렬이라고 쭉 부르는걸로 하자.
이 회전행렬은 몇가지 특수한 성질을 가지고 있다. 사실 이 행렬은 determinant가 1인 orthogonal 행렬이다. 역으로, orthogonal하면서 determinant가 1인 모든 행렬은 회전행렬이다. 따라서, 우리는 n차원의 회전 행렬 집합을 다음과 같이 정의할 수 있다:

SO(n)={R∈Rn×n∣RRT=I,det⁡(R)=1}\text{SO}(n) = \{\textbf{R}\in \mathbb{R}^{n\times n}|\textbf{R}\textbf{R}^T=\textbf{I}, \det(\textbf{R})=1 \}

SO(n)\text{SO}(n)은 special orthogonal group을 나타내는 용어로, n차원 공간에서의 회전행렬들로 이루어져있다. SO(3)\text{SO}(3)라고 하면 3차원 공간에서의 회전행렬 그룹을 의미하는 것이다.

여기서 orthogonal과 회전변환의 관계에 대한 정리를 잠깐 해보자.
사실 정확히 말하자면 모든 회전행렬은 직교행렬(orthogonal matrix)이고, 따라서 직교행렬의 성질을 계승한다. 직교행렬의 성질 중 하나가 벡터에 곱해도 그 벡터의 크기를 변화시키지 않는다는 것인데, 즉, 직교행렬 Q와 어떤 열벡터 v가 있으면 ||Qv|| = ||v||이다. 유클리드 공간 상에서 어떤 벡터의 크기는 변화하지 않았는데 좌표만 바뀌었다면 그건 회전 또는 반전이 일어났음을 의미하고, 따라서 사실 모든 직교행렬은 회전행렬이거나(det=1), *부적절한 회전 행렬이다(det=-1)
*영어로 improper rotation이라 부적절한 회전행렬이라고 번역하긴 했지만 그냥 회전+반사를 같이 행하는 변환을 저렇게 표현함.
*직교행렬의 성질 중 하나- det은 1이거나 -1이다(증명은 매우 간단함)
참고)

회전행렬의 역행렬은 반대방향으로의 회전을 의미하고, 역행렬=전치행렬(직교행렬의 특성)이므로 반대방향으로의 회전은 전치행렬과 같다.

a′=R−1a=RTa\textbf{a}' = \textbf{R}^{-1}\textbf{a} = \textbf{R}^{\text{T}}\textbf{a}

유클리디안 변환은 회전과 평행이동을 함께 고려한다. 월드좌표계에 있는 벡터 a\textbf{a}를 R\textbf{R}로 회전하고 t\textbf{t}만큼 평행이동을 하면 a’\textbf{a}’라는 벡터가 되고, 이걸 식으로 표현하면 a’=Ra+t\textbf{a}’ = \textbf{R}\textbf{a} + \textbf{t}이다.
여기서 t\textbf{t}는 평행이동(translation) 벡터이다. 회전과 비교했을 때, 평행이동 부분은 그냥 회전 후의 좌표에 평행이동 벡터를 단순히 더하면 끝으로 매우 간단한 것을 알 수 있다. 위 식을 통해 우리는 회전행렬 R\textbf{R}과 평행이동 벡터 t\textbf{t}를 이용해 좌표변환관계를 완전히 나타낼 수 있다.
좀 더 일반화를 해보자면, 서로 다른 좌표계 1과 2가 있을 때 두 좌표계 상에서 벡터 a\textbf{a}의 좌표를 a1\textbf{a}_1, a2\textbf{a}_2라고 하면 아래와 같이 두 좌표계 간 관계를 나타낼 수 있다.

a1=R12a2+t12\textbf{a}_1 = \textbf{R}_{12}\textbf{a}_2 + \textbf{t}_{12}

여기서 R12\textbf{R}_{12}는 “벡터를 좌표계 2에서 1로 바꿀때의 회전" (벡터를 돌리는게 아니고 벡터의 좌표를 변환해주는거임)을 의미한다. 벡터가 회전행렬의 오른쪽에 곱해지기 때문에 아래첨자는 오른쪽에서 왼쪽 순서로 읽어주도록 쓴다. 좌표변환은 원체가 엄청 헷갈리는데다가 특히나 여러 좌표계를 왔다갔다 하게되면 큰 혼란이 올 수 있으므로 일단 앞으로 우리가 쓸 표기법을 명확하게 하도록 하자. 1에서 2로의 회전행렬은 R21\textbf{R}_{21}로 쓴다. 정의하기에 따라 다르기때문에 책마다 표기법이 다를 수 있는데, 우리 책에서는 앞으로 이렇게 쓰기로 한다.

R12의 “벡터를 좌표계2에서 1로 바꿀때의 회전” 이라는게 기하학적으로 와닿지 않는? 불명확한 부분이 있을 수 있는데 이건 따로 정리

t12\textbf{t}_{12}의 기하학적 의미를 살펴보면, 이건 좌표계1의 시각에서 본 좌표계 1의 원점에서 좌표계2의 원점을 향하는 벡터를 의미한다. (즉 좌표계1 상에서 좌표계2의 원점의 좌표)
따라서 이걸 “1에서 2로의 벡터”라고 받아들이는 것을 추천한다.

벡터의 개념... 항상 원점이 꼬리 아닌가? 그러면 결국 좌표계 1의 원점에서 좌표계 2의 원점을 향하는 벡터의 월드좌표 = 좌표계 1 상에서 동일 벡터의 좌표 아닌가?? 원래 꼬리를 항상 원점으로 당겨와야하지않나? 확인 필요

좌표계 2의 원점에서 좌표계 1의 원점을 향하는 벡터의 좌표계 2 기준 벡터좌표인 t21\textbf{t}_{21}는 −t12-\textbf{t}_{12}와 같지 않다. 두 좌표계간 회전이 존재하기 때문이다.

오.. 정말? 아 하긴 좌표계는 평행이동이 아니고 로테이션도 포함되어있으니 당연한거구나

“지금 내 카메라의 좌표가 뭐냐”라고 한다면 일반적으로는 월드좌표계 W\text{W} 상에서 카메라계 C\text{C}의 원점을 가리키는 벡터 좌표를 의미하므로 tWCt_{\text{WC}}로 표현할 수 있다. 이건 방금 말했듯이 −tCW-t_{\text{CW}}와 같지 않고, 뒤에서 배우겠지만 −RCWtCW-R_{\text{CW}}t_{\text{CW}}와 같다.

2.1.3 변환행렬과 동차좌표계

위 식을 통해 우리는 유클리디안 공간 상에서의 회전과 평행이동을 완벽하게 표현할 수 있게 되었지만, 작은 문제가 남아있다.
바로 위 변환식은 선형이 아니라는 것! (지금 보여주겠지만 이건 상당히 끔찍한 문제이다)
우리가 R1\textbf{R}_1, t1\textbf{t}_1, 그리고 R2\textbf{R}_2, t2\textbf{t}_2 두 개의 변환을 수행한다고 해보자:

b=R1a+t1,c=R2b+t2\textbf{b} = \textbf{R}_1\textbf{a} + \textbf{t}_1, \quad\quad \textbf{c} = \textbf{R}_2\textbf{b} + \textbf{t}_2

그럼 a\textbf{a}에서 c\textbf{c}로의 변환은 이렇게 표현된다:

c=R2(R1a+t1)+t2\textbf{c} = \textbf{R}_2(\textbf{R}_1\textbf{a} + \textbf{t}_1) + \textbf{t}_2

즉, 여러번 변환을 하게되면 전혀 우아하지 않은 더러운 식이 나오게 된다. 이건 너무 보기 싫으니까(단순히 보기 싫어서만은 아니지만) 동차좌표(homogeneous coordinates)를 이용해 변환행렬이라는 걸 다음과 같이 정의해보자.

[a′1]=[Rt0T1][a1]≜T[a1]\left[\begin{matrix} \textbf{a}' \\ 1 \end{matrix}\right] = \left[\begin{matrix} \textbf{R} & \textbf{t}\\ \textbf{0}^{\text{T}} & 1 \end{matrix}\right] \left[\begin{matrix} \textbf{a} \\ 1 \end{matrix}\right] \triangleq \textbf{T}\left[\begin{matrix} \textbf{a} \\ 1 \end{matrix}\right]

이건 일종의 수학적인 트릭이라고 볼 수 있는데, 3차원 벡터의 끝에 1을 추가해 동차좌표라 부르는 4D 벡터로 바꿔준다. 이 4차원 벡터에 대해서는 회전과 평행이동을 한번에 단일 행렬로 표현할 수 있고, 이러면 전체 변환과정이 선형이 된다. 여기의 T\textbf{T}를 변환행렬이라고 부른다.

a\textbf{a}의 동차좌표를 a˜\textbf{\~a}로 나타내도록 하자. 그러면 동차좌표와 변환행렬을 사용해서 표현한 a\textbf{a}에서 c\textbf{c}로의 변환은 이런 예쁜 모양을 갖게된다.

b˜=T1a˜,c˜=T2b˜⇒c˜=T1T2a˜\textbf{\~b} = \textbf{T}_1\textbf{\~a},\quad \textbf{\~c} = \textbf{T}_2\textbf{\~b} \quad \quad \Rightarrow \textbf{\~c} = \textbf{T}_1\textbf{T}_2\textbf{\~a}

그런데 끝에 1을 붙였다 뗐다 하는 차이밖에 없는데 항상 기호로 동차좌표와 비동차좌표 벡터를 구별해서 표현하긴 귀찮으니까 여기서는 앞으로 그냥 구분하지않고 같은 표현으로 쓰도록 하겠다. 그냥 앞에 곱해지는 행렬이 열이 4개다 하면 아 이 벡터는 동차좌표구나 하면 된다. 예를들어 Ta\textbf{T}\textbf{a}라고 썼으면 a\textbf{a}는 동차좌표인거고(아니라면 계산이 안됨), Ra\textbf{R}\textbf{a}라고 썼으면 비동차좌표인 걸로 여기면 된다.

변환행렬 T\textbf{T}는 특수한 구조를 가진다. 좌상단이 회전행렬이고, 가장 오른쪽 열은 평행이동 벡터이고, 가장 밑 행은 0 0 0 1이다. 이 변환행렬의 집합은 special euclidean group에서 첫자를 따 SE로 표현된다.

SE(3)={T=[Rt0T1]∈R4×4∣R∈SO(3),t∈R3}\text{SE}(3) = \{\textbf{T} = \left[\begin{matrix} \textbf{R} & \textbf{t} \\ \textbf{0}^{\text{T}} & 1\end{matrix}\right] \in \mathbb{R}^{4 \times 4} | \textbf{R} \in \text{SO}(3), \textbf{t} \in \mathbb{R}^3\}

SO(3)\text{SO}(3)와 마찬가지로 변환행렬의 역행렬은 역변환을 의미한다. 앞에서와 같이, 우리는 T12\textbf{T}_{12}를 2에서 1로의 변환을 나타내도록 정의한다.

자, 복습해보자. 첫번째로 우리는 벡터와 벡터의 좌표 표현을 살펴보았고 벡터 간 연산을 소개했다. 좌표계간의 이동은 유클리디안 변환으로 설명되고, 이는 회전과 평행이동으로 이루어져있다. 회전은 회전행렬 SO(3)\text{SO}(3)로 묘사되고, 평행이동은 R3\mathbb{R}^3 벡터로 나타나진다. 마지막으로, 평행이동과 회전을 하나의 행렬로 한번에 나타내면 그게 변환행렬 SE(3)\text{SE}(3)이다.

2.2 실습: Eigen 사용하기

이번 강의의 실습 파트는 두 부분으로 이루어진다. 첫번째 파트에서는 어떻게 Eigen을 사용해 행렬과 벡터를 나타내는지, 그리고 회전행렬과 변환행렬을 어떻게 계산하는지를 설명할 것이다.

이번 실습의 코드는 “slambook2/ch3/useEigen”에서 찾아볼 수 있다.

Eigen (http://eigen.tuxfamily.org/index.php?title=Main_Page)은 C++ 오픈소스 선형대수 라이브러리로, 행렬에 대한 선형대수 연산을 최적화된 빠른 속도로 수행할 수 있도록 지원하며 선형 방정식을 푸는 것과 같은 여러 함수들을 제공한다.
많은 상위 소프트웨어 라이브러리(g2o, Sophus, etc..) 들도 행렬 연산을 위해 Eigen을 사용한다.
PC에 Eigen이 깔려있지 않다면 다음의 커맨드로 설치를 해보자.

sudo apt-get install libeigen3-dev

우리 책에서 쓰이는 대부분의 라이브러리들은 우분투 소프트웨어 센터에 등록되어있으므로 apt 명령어를 사용해 손쉽게 설치 가능하다. 저번 강의에서 우리는 라이브러리가 헤더 파일과 라이브러리 파일로 이루어져있다는 것을 배웠다. Eigen은 오로지 헤더파일들로만 빌드된 특이한 라이브러리이다. 이말은, .so나 .a같은 바이너리 파일 없이 헤더 파일만 위치시키면 가져다 쓸 수 있다는 말이다. 즉 라이브러리 파일을 링크시킬 필요 없다.

그럼 이제 아래의 코드조각을 통해 Eigen을 연습해보자!

2.3 회전 벡터와 오일러각

2.3.1 회전 벡터

이제 다시 이론적인 부분으로 넘어가보자. 회전 행렬을 사용한 4X4 변환 행렬만으로 6DoF의 3D 강체의 움직임을 나타내기 충분할까? 이 행렬 표현은 다음의 명확한 단점을 가지고 있다.
1. SO(3)는 9개의 값을 가진 회전 행렬이지만, 3D 회전은 사실 3자유도 운동이기 때문에 이 행렬 표현은 불필요하게 많은 값을 사용한다는 것을 알 수 있다. 변환행렬 또한 6자유도의 움직임을 16개의 값으로 표현하는 낭비를 하고 있다. 뭔가 더 콤팩트한 표현이 없을까?
2. 회전 행렬은 determinant가 1인 orthogonal matrix여야 한다는 존재 자체에 대한 기본적인 constraints를 가진다. 변환 행렬도 마찬가지 (R 부분이 위 constraints를 만족해야한다는걸 말하는건가?). 이 constraints는 회전/변환 행렬을 추정하거나 최적화하기 어렵게 만든다.

따라서, 회전이나 평행이동을 표현할 수 있는 좀 더 간단하고 압축적인 표현을 찾아볼 필요가 있다. 예를 들자면.. 회전을 3차원 벡터로, 변환을 6차원 벡터로 표현할 순 없을까? 회전을 회전축과 회전각으로 표현할 수 있다는 것은 명백하다. 따라서, 우리는 벡터-회전축과 평행한 방향이면서 길이가 회전각과 같은-를 사용할 수 있다. 이를 회전 벡터 (또는 angle-axis/axis-angle)이라 부른다. 이렇게 하면 3차원 벡터만으로 회전을 나타낼 수 있다. 비슷하게, 우리는 회전 벡터와 평행이동 벡터를 합쳐서 변환 행렬을 표현할 수 있다. 이렇게 되면 6차원이 된다. R\textbf{R}이라고 표현되는 회전을 생각해보자. 이게 회전 벡터로 표현된거라면, 회전축이 단위길이의 벡터 n\textbf{n}이고, 회전각이 θ\theta라고 가정했을 때, 벡터 θn\theta\textbf{n}또한 이 회전을 나타낼 수 있다(?). 그럼, 이 두 표현 간의 연결고리가 무엇인가? 사실, 이 둘 간의 관계를 유도하는 것은 매우 간단하다. 로테이션 벡터-행렬로의 변환은 로드리게스 수식 (Rodrigues' formula)을 이용하여 수행할 수 있다. 자세한 유도는 살짝 복잡하니까 생략하고, 변환 수식만 알려주겠다. (자세한 유도는 링크 참고: https://en.wikipedia.org/wiki/Rodrigues%27_
rotation_formula, 근데 어차피 뒤에서 리 대수 관점에서 유도 한번 해줄거)

R=cos⁡θI+(1−cos⁡θ)nnT+sin⁡θn∧\textbf{R} = \cos{\theta}\textbf{I} + (1-\cos{\theta})\textbf{n}\textbf{n}^T + \sin{\theta}\textbf{n}^{\wedge}

∧^\wedge 기호는 벡터를 skew-symmetric으로 변환해주는 연산자이고, 앞에서 설명했다. 반대로 우리는 회전 행렬로부터 회전 벡터를 계산할 수도 있다.
코너 θ\theta에 대해, 양 변에 trace를 취하면, (뭔소리야?)

tr(R)=cos⁡θtr(I)+(1−cos⁡θ)tr(nnT)+sin⁡θtr(n∧)=3cos⁡θ=(1−cos⁡θ)=1+2cos⁡θ\text{tr}(\textbf{R}) = \cos{\theta}\text{tr}(\textbf{I}) + (1-\cos{\theta})\text{tr}(\textbf{n}\textbf{n}^T) + \sin{\theta}\text{tr}(\textbf{n}^{\wedge}) \\ = 3 \cos{\theta} = (1-\cos{\theta}) \quad\quad\quad\quad\quad\quad\quad\quad \\ = 1+2\cos{\theta} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad

따라서,

θ=arccos⁡(tr(R)−12)\theta = \arccos\left({{\text{tr}(\textbf{R})-1}\over{2}}\right)

축 n\textbf{n}에 따라, 왜냐면 회전축은 회전 후에도 바뀌지 않으므로,

Rn=n\textbf{R}\textbf{n} = \textbf{n}

따라서, 축 n\textbf{n}는 회전행렬 R\textbf{R}의 고유값(eigenvalue) 1(??)에 해당하는 고유벡터이다. (왜?)
고유값, 고유벡터의 기하학적 의미 복습(아 그냥 정의상 당연한거지 참)
이 식을 풀고 노말라이즈 해주면 그 솔루션이 바로 회전축이다. 이렇게 알아본 두 변환 수식은 뒷장에서도 나올 것이고, 이는 SO(3)\text{SO}(3) 상에서 리 그룹과 리 대수 간의 간계와 정확히 일치한다는 것을 발견하게 될 것이다!

2.3.2 오일러각

그럼 이제 오일러각 얘기를 좀 해보자.
그게 회전 행렬이든 회전 벡터읻ㄴ, 그들이 회전을 묘사할 수 있다고 해도, 그 숫자들 만으로 회전을 상상하는 것은 어려운 일이다. 그 값들이 바뀌었을 때, 우리는 물체가 어떤 방향으로 돌지 모른다. 오일러각은 회전을 굉장히 직관적인 방식으로 묘사해준다. 오일러각은 3개의 기본축(primal axis)을 사용하여 회전을 각 축을 중심으로 한 3개의 회전으로 분해한다. 사람은 한 축 회전 프로세스는 쉽게 상상할 수 있으므로.
하지만, 분해 방법은 매우 다양하기 때문에 오일러각에 대해서는 매우 다양한 대체들과 헷갈리는 정의들이 존재한다. 예를 들어 우리는 일단 첫번째로 X축에 대해서 회전을 하고, 그 다음 Y축, 그리고 Z축 순- 즉 XYZ 순서로- 회전을 할 수도 있는데, 근데 ZYZ나 ZYX 등등도 가능하다. 그리고 우리는 회전이 완전 고정축에서 이루어지는지, 아니면 회전 이후의 축을 기준으로 이루어지는지도 구별해야한다.

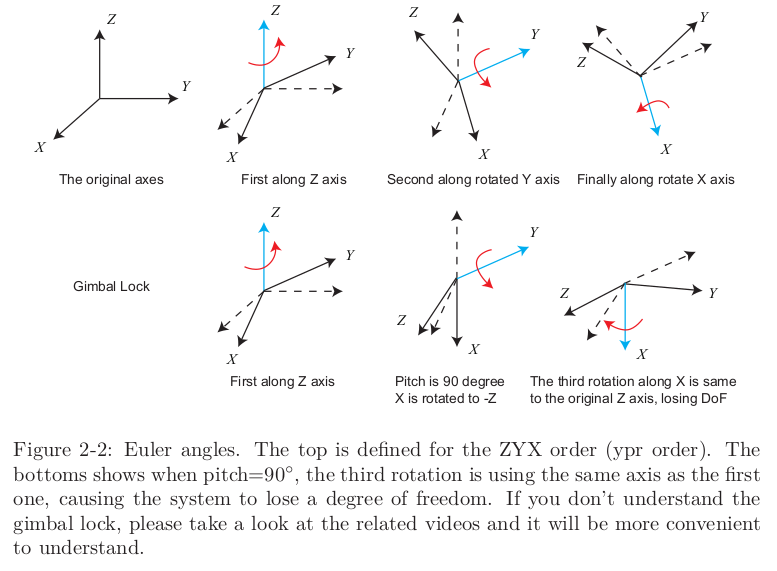
이렇게 불명확한 축 순서로 인해 사용에 상당한 문제점들이 발생하는데, 다행히도 특정 연구 분야 끼리는 공통된 오일러각 정의를 사용한다. 여러분도 아마 "피치 각 (pitch angle)"이나 "요 각 (yaw angle)"과 같은 항공용어를 들어본 적이 있을텐데, 이것이 오일러각 중 가장 일반적으로 쓰이는 yaw-pitch-roll 각이다. 이건 ZYX축 순서의 회전을 사용하는데, 따라서 ZYX 오일러각을 예시로 들어보자. 강체의 정면 (우리를 향한)이 X축이라고 가정하고, 오른쪽 방향이 Y, 위쪽 방향이 Z축이라고 해보자. (그림 2-2를 보면 됨) 그러면, ZYX 각은 다음의 세 축을 따라 회전을 분해하는 것이다.
1. 우선은 z축을 기준으로 회전해서 요 각 θyaw=y\theta_{yaw}=y이도록 맞춰줌(?)
2. 그 다음 회전된 상태의 Y축을 기준으로 다시 회전해줘서 피치 각 θpitch=p\theta_{pitch}=p을 만들어줌
3. 마지막으로 회전된 상태의 X축을 기준으로 θroll=r\theta_{roll}=r을 만들어주면 끝

이렇게 하면, 우리는 [y,p,r]T[y, p, r]^T와 같은 3차원의 벡터를 이용해 어떤 회전이든 표현할 수 있다. 그리고 이 벡터는 굉장히 직관적이다. 우리는 이 벡터를 보면 회전과정을 상상할 수 있다. 다른 오일러각도 순서에 따라 다양하지만, 위에서 본 ypr각이 제일 널리 쓰인다. 다른 오일러각은 축순서와 함께 언급된다. 예를들어 ypr각은 ZYX이고, XYZ, ZYZ와같은 오일러각도 있을 수 있지만 얘네는 ypr각 같은 별도의 이름은 없다. 각 분야마다 고유의 좌표방향과 오일러각 습관이 있다.
오일러각의 제일 큰 단점은 짐벌락(Gimbal lock)이라는 아주 유명한 문제이다. ypr 케이스에서, 만약 피치각이 +-90도이면, 처음 회전과 세번째 회전은 같은 축을 이용하게 되고, 그러면 시스템의 자유도가 3에서 2로 줄어들게 된다. 이를 singularity problem이라고 하고

profile
yeonsoo
to be enterprising
이전 포스트

Introduction to Visual SLAM From Theory to Practice (1)

0개의 댓글