Logistic Regression as a Neural Network
Binary Classification
로지스틱 회귀를 통해 아이디어를 전달한다.
고양이 사진으로 예를 들어본다. 이미지를 인식하기 위해서 고양이일때는 1, 고양이가 아닐 때는 0으로 레이블을 출력하려고 한다. 이미지를 저장하기 위해서는 R,G,B 채널에 대응하는 세 개로 분리된 행렬을 사용한다.
RGB에 해당하는 각각의 특징 벡터가 있고, 만약 input이미지가 64x64픽셀로 된 이미지라면 이미지의 차원은 64x64x3이 될 것이다.
Logistic Regression
지도학습 문제에서 결과값 레이블 y가 0,1인 경우 사용되는 알고리즘이다. 즉, 이진 분류 문제의 경우이다.
선형회귀에서 사용하는 방법대로 y hat=tr(W)X+b을 사용할 수도 있지만, y hat이 0과 1사이에 있어야하므로 적합한 방식이 아니다.
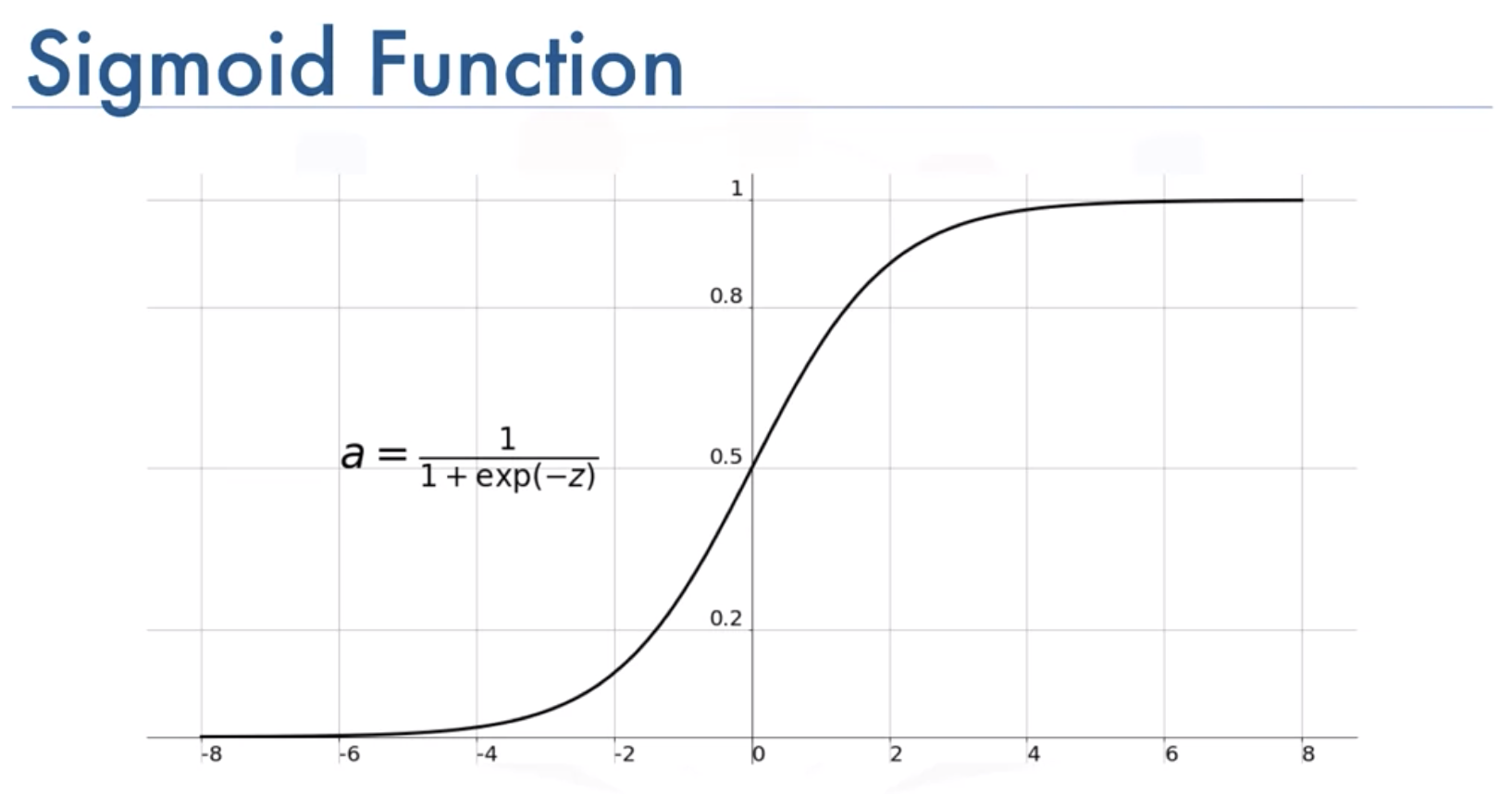
그래서 Z=tr(W)x+b에 sigmoid함수를 적용한다. Z가 매우 큰 경우 Z의 시그모이드는 1에 가까운 값이 되고, Z가 매우 작으면 0에 가까운 값이 된다. 그러므로 로지스틱 회귀분석을 도입하는 경우에는 y hat이 Y=1이 되는 값을 찾는 것이 중요하다.
Logistic Regression Cost Function
-
비용함수
loss함수는 true label y를 값는 경우, 얼마나 정확히 y hat 결과를 갖는지 정의할 때 사용한다. -
Loss Function
표현이 잘 될지는 모르겠지만 작성해본다.
L(y hat, y)= -(ylogyhat + (1-y)log(1-y hat))
이 때, y=1인 경우 L(y hat, y)= -logyhat이 된다. 즉, y가 1인 경우 y hat은 1에 가까운 수가 좋은 것이다. 반대로 y=0인 경우 y hat은 0에 가까운 수가 좋은 것이다.
강의를 제대로 이해한 것인지는 모르겠는데, 자코비언 함수를 통해 로지스틱 회귀의 전체 비용함수를 나타내는 것인데, 그 parameter는 loss function의 parameter임(W, B). 그래서 이를 줄이는 것이 전체 모델의 비용 J를 줄이게 된다.
