군집분석(Clustering)의 개요
각 개체에 대해 관측된 여러 개의 변수 값들로부터 n개의 개체를 유사한 성격을 가지는 몇 개의 군집으로 집단화, 형성된 군집들의 특성을 파악하여 군집들 사이의 관계 분석하는 다변량분석 기법
-
특성에 따라 객체들을 여러 개의 배타적인 집단으로 나누는 것
-
군집 개수나 구조에 대한
가정 없이데이터로부터 거리를 기준으로 군집화 -
소비자들의 상품구매행동, life style 에 따른 소비자군 분류에 활용
-
반응변수가 없으며, 개체들 간의 유사성 (similarity)에만 기초한다. -
이상값 탐지에 사용한다.
-
나누는 방법에 따른 군집화 구분
- 임의적 방법 : 논란여지 많으나 많이 사용되어 왔다.
- 통계적 기법 활용 : 1, 2세대 알고리즘 이용해 사용돼왔으나 실무적용성에 대한 논란
💡 계층적 군집
◽ 계층적 군집
가장 유사한 개체를 묶어 나가는 과정 반복, 원하는 개수의 군집 형성 방법
-
계통도 또는 덴드로그램(dendrogram)의 형태로 결과 주어진다.
-
각 개체는 하나의 군집에만 속한다.
-
유사성에 다양한 정의가 있다.
-
군집간의 연결법에 따라 결과 달라질수도 있다.
◽ 계층적군집 형성 방법
◾ 병합적 (agglomerative/ Bottom Up) 방법
여러개의 군집에서 점차 줄여나간다. (군집병합)
-
한 개의 항목에서 시작한다.
-
형성 매 단계마다 모든 그룹 쌍 간의 거리 계산하여 가까운 순 으로 병합 수행을 한다.
-
한 개 그룹만 남을 때까지 혹은 종료 조건 될 때까지 반복한다.
-
항목간 상대적 거리가 가까울수록 유사성 (similarity) 이 높다.
-
R에서 agnes(), mclust() 함수를 이용한다.
◾ 분할적 (divisive/ Top Down) 방법
한개에서 여러개로 군집수를 늘려간다.
-
하나의 군집에서 n개 군집으로 분리
-
R에서 diana(), mona() 함수를 이용한다.
◽ 덴드로그램 (dendrogram)
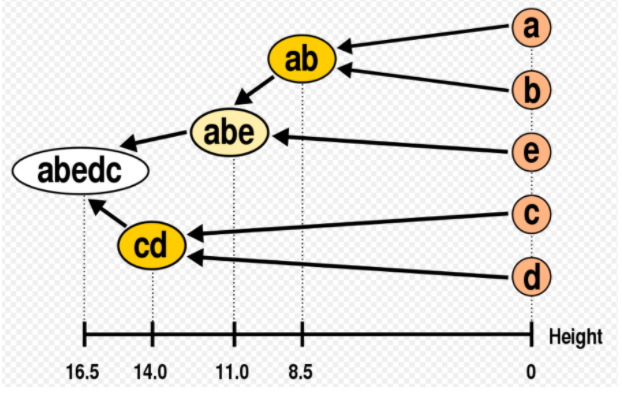
-
계층적 군집의 결과는 덴드로그램 (dendrogram)으로 항목간의 거리, 군집간의 거리 알 수 있다.
-
군집 내 항목 간 유사정도 파악 ➡️ 군집의 견고성 해석 가능
◽ 두 군집간의 거리 측정 방법
◾ 최단연결법 | 단일연결법 (single linkage method)
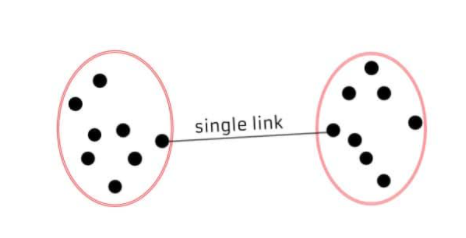
각 군집에서 하나씩 관측값을 뽑았을 때 나타낼 수 있는 거리의 최소값으로 측정한다.
-
사슬 모양 생길 수 있다.
-
고립된 군집 찾는데 중점을 둔다.
◾ 최장연결법 | 완전연결법 (complete linkage method)
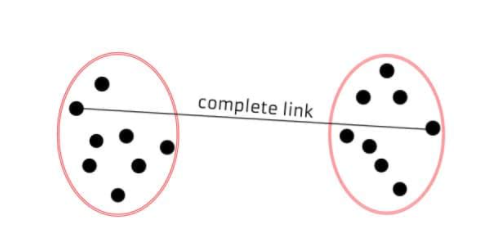
각 군집에서 하나씩 관측값 뽑았을 때 나타낼 수 있는 거리의 최대값으로 측정한다.
-
같은 군집에 속하는 관측치는 알려진 최대 거리보다 짧다.
-
군집들의 내부 응집성에 중점을 둔다.
◾ 중심연결법 (centroid linkage)
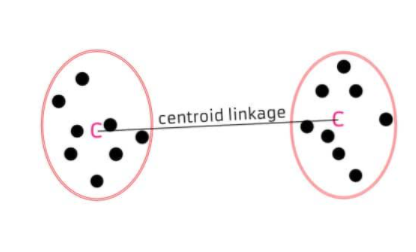
두 군집의 중심 간의 거리 측정
-
두 군집의 중심간 거리를 군집간 거리로 한다.
-
군집이 결합될 때, 새로운 군집의 평균은 가중평균을 통해 구해진다.
◾ 평균연결법 (average linkage)
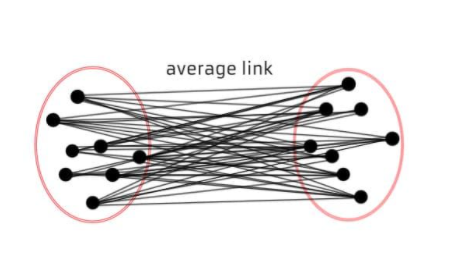
-
모든 항목에 대한 거리 평균을 구하면서 군집화를 수행한다.
-
계산량이 불필요하게 많아질 수 있다.
◾ 와드연결법 (ward linkage)
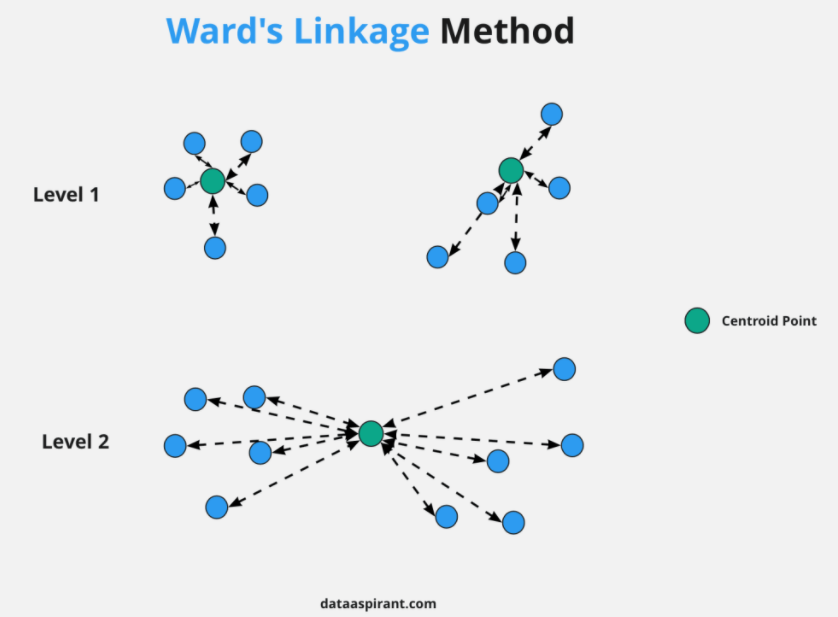
-
군집내의 오차제곱합에 기초하여 군집을 수행한다.
-
군집이 병합되면 오차제곱합은 증가하는데, 증가량이 가장 작아지도록 군집을 형성한다.
-
크기가 비슷한 군집끼리 병합하게 되는 경향이 있다.
- R에서의 계층적 군집 분석
> d <- dist( data, method="euclidean" ) # 거리 행렬을 제공하는 함수
> h <- hclust( d, method="ave" ) # hclust() : 계층적 군집 분석 수행
# method : 군집간 거리측정 방식 지정
> plot(h) # 덴드로그램으로 시각화
> cutree(h, k=6) # 계층적 군집 결과를 원하는 그룹의 수(k)로 나누어 볼 수 있다.
# rect.hclust() 함수를 통해 원하는 그룹수로 나누어 시각화가 가능하다.◽ 거리 (모든 변수가 연속형인 경우)
◾1) 수학적 거리
데이터간 유사성 측정을 위해 사용, 통계적 개념이 내포되어있지 않다, 변수들의 산포정도 감안하지 않는다.
-
유클리드(유클리디안, Euclidean) 거리
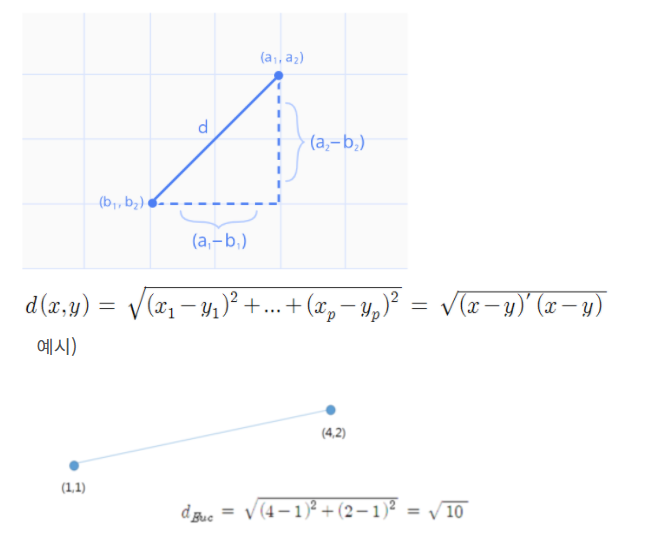
-
두 점 사이의 거리로, 가장 직관적이고 일반적인 거리 개념
-
방향성이
고려되지 않은단점이 있다.
-
-
맨하탄(Manhattan) 거리

- 두 점의 좌표간의 절대값 차이를 구하는 것이다.
- 맨하튼의 격자 무늬 도로에서 유래되었다.
◾2) 통계적 거리
표준화 (Statistical) 거리 :
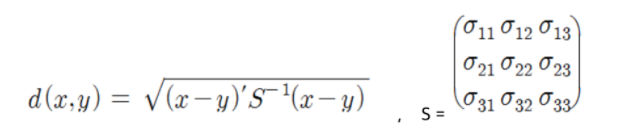
- 해당 변수의 표준편차로 척도 변환 후 유클리디안 거리를 계산
마할라노비스 거리
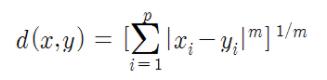
- 변수 표준화 + 변수 간의 상관성 (분포 형태) 고려
- 민코우스키(Minkowski) 거리

- 체비셰프 거리 (체스보드 거리, 최고 거리)

- 캔버라 거리
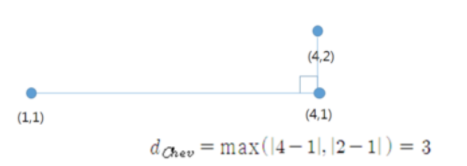
그 외) 유사성 측도인 코사인 거리, 상관계수 등
💡비계층적 군집방법
◽ 비계층적 군집방법의 정의 및 특징
-
n개의 개체를 g개의 군집으로 나눌 수 있는 모든 방법을 점검해 최적화한 군집을 형성한다.
-
자료의 크기에
제약이 없다.
◽ 비계층적 군집방법의 장점과 단점
| 장점 | 단점 |
|
- 주어진 데이터의 내부구조에 대한 사전정보 없이 의미있는 자료구조를 찾을 수 있다. - 다양한 형태의 데이터에 적용이 가능하다. - 분석방법 적용이 용이하다. |
- 가중치와 거리정의가 어렵다. - 초기 군집수를 결정하기 어렵다. - 사전에 주어진 목적이 없으므로 결과 해석이 어렵다. |
◽ K-평균 군집 분석 (K-means Clustering)
원하는 수 만큼 초기값을 지정하고, 각 개체를 가까운 초기값에 할당하여 군집을 형성 한 후, 각 군집의 평균을 재계산하여 초기값을 갱신한 뒤 갱신된 값에 대해 위의 할당 과정을 반복하여 k개의 최종군집을 형성하는 방법
-
거리계산을 통해 군집화가 이루어지므로 연속형 변수에 활용이 가능하다.
-
K개의 초기 중심값은 임의로 선택 가능, 가급적 멀리 떨어지는 것이 바람직하다.
-
초기 중심값이 일렬(위아래, 좌우)로 선택되면 군집 혼합이 되지 않고 층으로 나뉠 수 있으니 주의해야 한다.
-
초기 중심값의 선정에 따라 결과가 달라진다. ➡️ 따라서 코딩할때도 seed값을 고정한다.
-
초기 중심으로부터의 오차 제곱합을 최소화하는 방향으로 군집이 형성되는 탐욕적(greedy) 알고리즘 이므로 안정된 군집은 보장하나
최적이라는 보장은 없다.
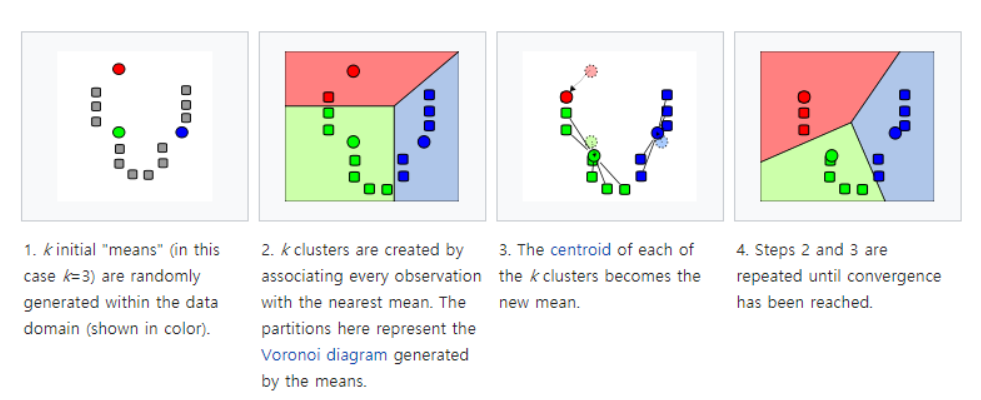
◽ K-means Clustering 과정
① k개의 객체를 임의로 선택하여 군집의 중심으로 삼는다.
② 가장 가까운 중심으로 각 개체를 할당한다. (오차제곱합이 최소가 되도록)
③ 각 군집의 중심을 갱신한다. 즉 각 군집의 seed값을 다시 계산한다.
④ 군집 중심의 변화가 거의 없을 때까지 ②~③ 과정을 반복 한다.
◽ K-평균 군집 분석의 장점과 단점
| 장점 | 단점 |
| - 알고리즘이 단순하며, 빠르게 수행되어 분석 방법 적용이 용이하다. - 계층적 군집분석에 비해 많은 양의 데이터를 다룰 수 있다. - 내부 구조에 대한 사전정보가 없어도 의미있는 자료구조를 찾을수 있다. - 다양한 형태의 데이터에 적용 가능하다. |
- 군집의 수, 가중치와 거리 정의가 어렵다. - seed값에 따라 결과가 달라질 수 있음(항상 일정한 결과 X) - 사전에 주어진 목적이 없으므로 결과 해석이 어렵다. - 잡음이나 이상값의 영향을 많이 받는다. - 볼록한 형태가 아닌 (non-convex) 군집이(예를 들어 U형태의 군집) 존재할 경우에는 성능이 떨어짐 |
-
군집의 수(k)는 미리 정해야 한다.
-
초기 중심점들은 멀리 떨어져 있는 것이 바람직하며, 초기값에 따라 군집 결과가 크게 달라질 수 있다.
-
매 단계마다 오차제곱합을 최소화하는 방향으로 군집이 형성되는 탐욕적 알고리즘이다.
-
안정적 군집이 보장되나, 최적을 보장하지는 못한다.
◽ R에서의 k-평균 군집 수행
> kmeans(data, 군집수) or kcca() or cclust() # k-평균 군집 수행
> plot() # 시각화
> table() # 정오분류표◽ 혼합 분포 군집
데이터가 k개의 모수적 모형(정규분포 혹은 다변량 분포를 가정)의 가중합으로 표현되는 모집단 모형으로 부터 나왔다는 가정하에서, 모수와 함께 가중치를 자료로부터 추정하는 방법이다.
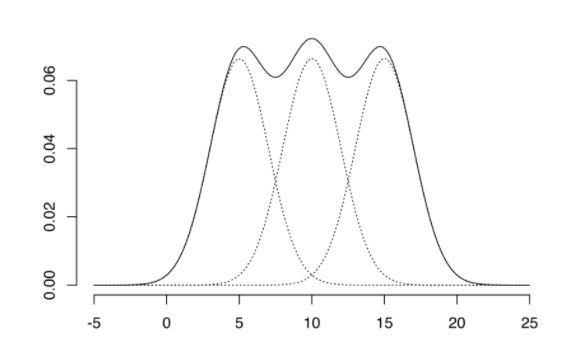
- 각 데이터는 k개의 추정된 모형 중 어느 모형에 속할 확률이 높은지에 따라 분류한다.
◽ K-means vs 혼합분포군집
-
두 방법 모두 1개의 클러스터로 출발한다.
-
k-means은 클러스터를 중심거리로, EM은 MSL로 거리측정
-
클러스터를 늘리면 이전보다 클러스터 중심에서 평균 거리는 짧아지고 EM은 우도가 커진다.
-
혼합분포군집은 확률분포를 도임하여 군집을 수행하는 점이 다르다.
-
EM 알고리즘을 이용한 모수 추정에서 데이터가 커지면 수렴하는데 시간이 오래걸리고, 군집의 크기가 작으면 추정의 정도가 떨어진다.
-
k-mean 평균과 같이 이상값에 민감하다.
◽ EM 알고리즘
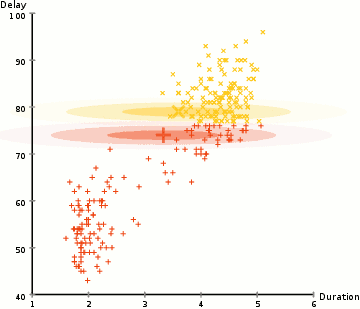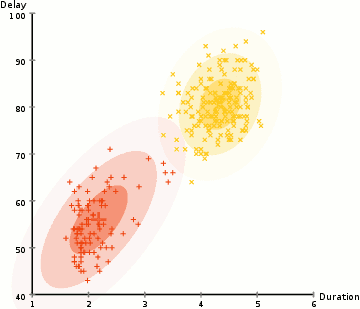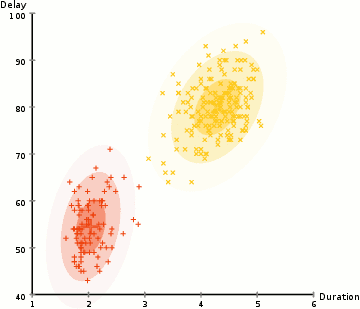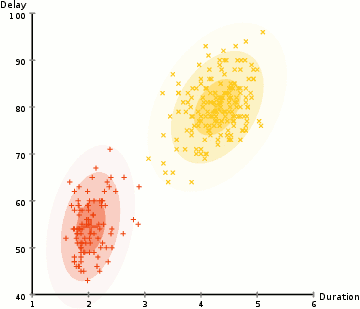
-
모집단을 구성하는 각 집단의 분포는 정규분포를 따른다고 가정, 각 자료가 어느 집단에 속하는지에 대한 정보를 잠재변수 Z라 한다.
-
갱신된 모수 추정치에 대해 위 과정을 반복한다면 수렴하는 값을 얻게되고, 이는 최대 가능도 추정치로 사용될 수 있다.
-
EM(Expectation Maximizaion) 알고리즘의 진행 과정
① E-단계 :잠재변수 Z의 기대치 계산
② M-단계 : Z의 기대치를 이용하여 파라미터를 추정
③ E~M 단계를 반복하며 모수 추정치에 수렴하는 값을 얻는다.
-
E-단계: 각 자료에 대해 Z의 조건부분포(어느 집단에 속할지에 대한)로부터 조건부 기댓값을 구할 수 있다.
-
M-단계: 관측변수 X와 잠재변수 Z를 포함하는 (X, Z)에 대한 로그-가능도함수(이를 보정된(augmented) 로그-가능도함수라 함)에 Z 대신 상수값인 Z의 조건부 기댓값을 대입하면, 로그-가능도함수를 최대로 하는 모수를 쉽게 찾을 수 있다.
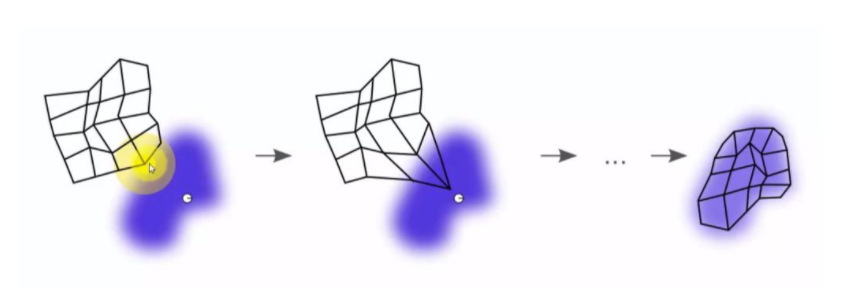
◽ SOM(Self-Organizing Maps, 자기조직화지도)
-
비지도 신경망으로 고차원의 데이터를 이해하기 쉬운 저차원의 뉴런으로 정렬해 지도의 형태로 형상화하는 것으로 입력 변수의 위치 관계를 그대로 보존한다는 특징이 있다.
-
시각적인 이해가 쉽고, 실제 데이터가 유사하면 지도상에서 가깝게 표현돼 패턴 발견, 이미지 분석 등에서 뛰어난 성능을 보인다.
-
경쟁 학습으로 각각의 뉴런이 입력 벡터와 얼마나 가까운가를 계산하여 연결 강도를 반복적으로 재조정하여 학습한다.
-
입력 패턴과 가장 유사한 경쟁층 뉴런이 승자가 된다. (승자 독식 구조)
- 역전파 알고리즘 등을 이용하는 인공신경망과 달리 단 하나의 전방 패스를 사용함으로써 수행속도가 매우 빠르다.
◽ SOM의 활용
- Find structures in data(구조 탐색) : 데이터의 특징을 파악하여 유사 데이터를 군집
- Dimension Reduction(차원 축소) & Visualization(시각화) : 차원을 축소하여 통상 2차원 그리드에 매핑하여 시각적으로 이해시킨다.
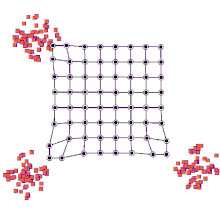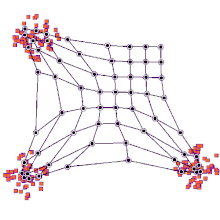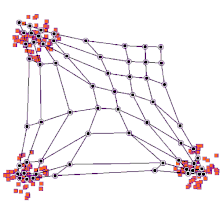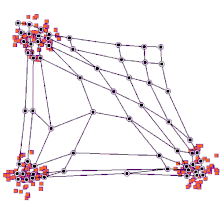
◽ SOM의 학습알고리즘
-
단계1. SOM 맵의 연결강도 초기화
-
단계2. 입력 벡터 제시
-
단계3. <span style="color:red"입력 벡터>와 프로토타입 벡터 사이의 유사도를 계산(유클리드 거리 이용)
-
단계4. 가장 거리가 짧은 프로토타입 벡터(BMU) 탐색
-
단계5. BMU 와 그 이웃들의 연결강도를 재조정
-
단계6. 단계2~5를 반복한다.
◽ R을 이용한 SOM 군집분석
> som( data, grid=somgrid(), rlen=100, alpha=c(0.05, 0.01), init, toroidal=FALSE, keep.data=TURE )
> summary() # SOM 군집 분석 결과 요약
> plot() # 그래프를 통한 시각화 (plot.kohonen의 SOM plot은 다양한 형식을 지원)
> unit.distances() # SOM 군집 분석 결과, 유닛 사이의 거리계산법본 게시물에 포함된 내용은 한국데이터산업진흥원에서 발행한]
[wikipedia.org/wiki,데이터 분석 전문가 가이드, 2019년 2월 8일 개정]에 근거한 것임을 밝힙니다.