- 학습 방법과 모델
- 모델 학습 방법(Model-Based Learning)
- 모델 기반 학습 (Model-Based Learning)
1) 데이터로부터 모델을 생성하여 분류/예측 진행
2) Linear Regression, Logistic Regression
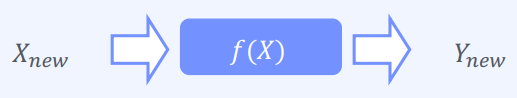
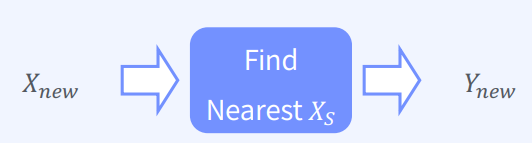
- 사례 기반 학습 (Instance-Based Learning)
1) 별도의 모델 생성 없이 인접 데이터를 분류/예측에 사용
2) Lazy Learning (사례 기반 학습은 별도의 모델 생성 없이 인접한 데이터를 분류 또는 예측에 사용)
3) 모델을 미리 만들지 않고, 새로운 데이터가 들어오면 계산을 시작
4) 이러한 방식은 KNN, Naive Bayes 분류기와 같은 알고리즘에서 사용
- KNN의 정의
K- Nearest Neighbors
1) K 개의 가까운 이웃을 찾는다.
2) 학습 데이터 중 K개의 가장 가까운 사례를 사용하여 분류 및 수치 예측
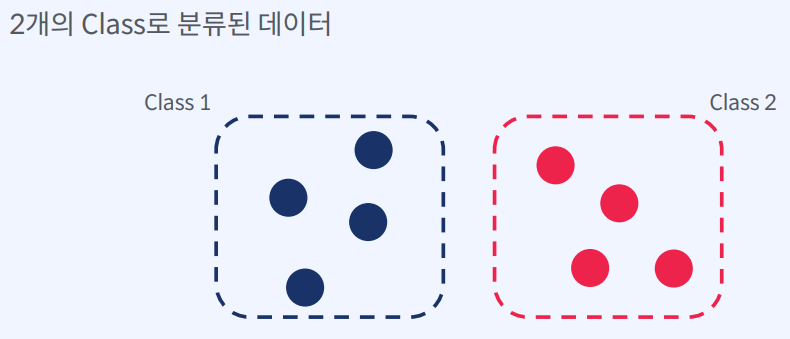
- 새로운 데이터를 입력 받음
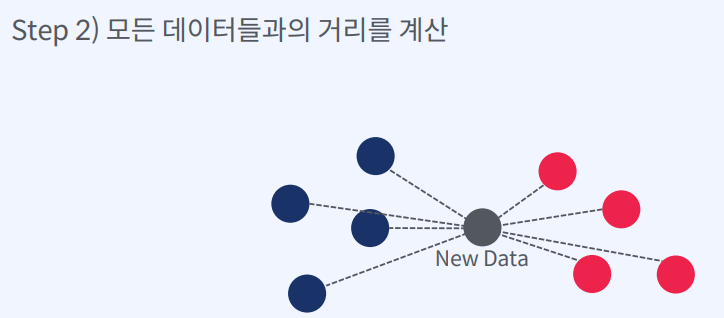
- 모든 데이터들과의 거리를 계산
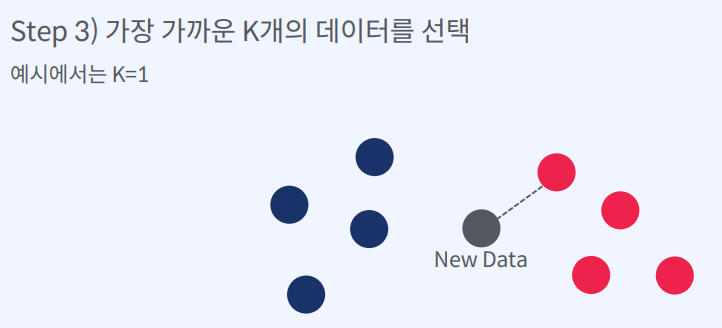
- 가장 가까운 K개의 데이터를 선택
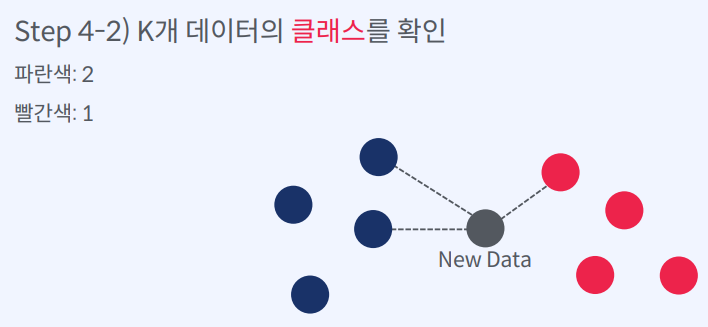
- K개 데이터의 클래스를 확인
- 다수의 클래스를 새로운 데이터의 클래스로 예측
즉, K-Nearest Neighbors (KNN) 알고리즘은 새로운 데이터가 들어오면,
모든 학습 데이터와의 거리를 계산하여 가장 가까운 K개의 데이터를 선택하고,
이 K개의 데이터의 클래스를 확인하여 다수의 클래스를 새로운 데이터의 클래스로 예측하는 방식으로 작동
KNN은 사례 기반 학습 중 하나로, 모델을 미리 학습하지 않고,
새로운 데이터가 들어올 때마다 계산을 시작합니다.
이는 게으른 학습(Lazy Learning)이라고도 불립니다.
KNN은 주로 분류 및 수치 예측 문제에서 사용됩니다.
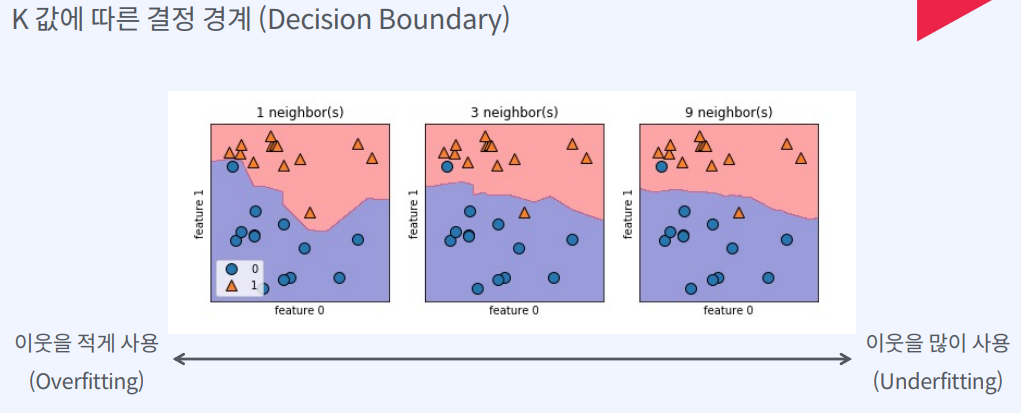
이때 K값이 작으면 결정 경계가 불안정해지지만, K값이 커지면 과적합이 일어날 수 있습니다.
따라서 적절한 K값을 찾는 것이 중요합니다.




- 최적의 K값 설정
Cross Validation
1) 교차 검증을 통해 제일 성능이 좋은 K 를 선택해야 한다.
2) 예를 들어서 1~10 사이의 K 중 제일 성능이 좋은 K를 선택
즉, Cross Validation은 KNN을 비롯한 다양한 머신 러닝 모델의 성능을 평가하고, 최적의 하이퍼파라미터 값을 찾는 데 사용된다.
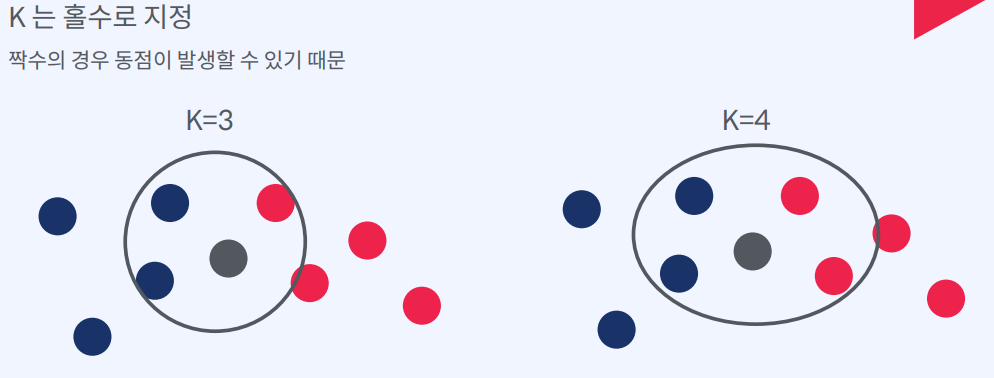

교차 검증은 일반적으로 다음과 같은 단계로 수행됩니다.
- 데이터셋을 훈련 세트와 테스트 세트로 나눕니다.
- 훈련 세트를 K개의 fold로 나눕니다.
- K개의 fold 중 하나를 검증 세트로 선택하고, 나머지 K-1개의 fold로 모델을 학습시킵니다.
- 검증 세트로 모델을 평가합니다.
- 3~4단계를 K번 반복하여 각 fold를 검증 세트로 선택하고, 모델을 학습시키고, 평가합니다.
- K번 평가한 결과를 평균하여 모델의 성능을 추정합니다.
KNN에서 최적의 K값을 선택하기 위해서는 교차 검증을 통해 각 K값의 성능을 평가하고, 최적의 K값을 선택해야 합니다. 예를 들어, 1부터 10까지의 K값 중에서 가장 성능이 좋은 K값을 선택할 수 있습니다. 이때, 일반적으로 K값에 대한 그리드 서치(Grid Search)를 사용하여 최적의 K값을 찾을 수 있습니다.
- 거리의 종류
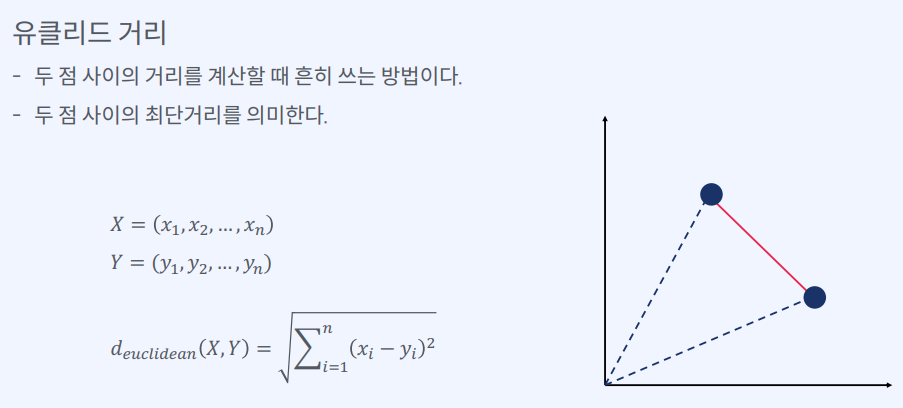
- 유클리드 거리(Euclidean Distance)
1) 두 점 사이의 거리를 계산할 때 흔히 쓰는 방법이다.
2) 두 점 사이의 최단거리를 의미한다
두 점을 각각 (x1, y1), (x2, y2)라고 할 때, 유클리드 거리는 √((x2-x1)² + (y2-y1)²)로 계산됩니다. 이는 두 점 사이의 최단 거리를 의미
- 맨해튼 거리(Manhattan Distance)
1) 한 번에 한 축 방향으로 움직일 수 있을 때 두 점사이의 거리
2) 그리드 형태에서 두 점 사이의 거리를 계산할 때 사용
두 점을 각각 (x1, y1), (x2, y2)라고 할 때, 맨해튼 거리는 |x2-x1| + |y2-y1|로 계산됩니다. 이는 두 점을 대각선 방향으로 이동할 수 없을 때, 실제 이동해야 하는 거리를 의미

K- Nearest Neighbors 장점
- 학습 과정이 없다. 즉, 모델 생성 및 학습에 드는 시간이 없다.
- 결과를 이해하기 쉽다. 즉, 예측 결과가 어떤 이웃 데이터들을 바탕으로 결정되었는지 쉽게 이해할 수 있다.
K- Nearest Neighbors 단점
- 데이터가 많을 수록 시간이 오래 걸린다. 새로운 데이터가 들어올 때마다 모든 훈련 데이터와 거리를 계산해야 하기 때문
- 지나치게 데이터에 의존적이다.
훈련 데이터에 존재하지 않는 새로운 데이터를 예측할 때는 부적합한 결과를 도출할 수 있습니다.
또한, 데이터의 분포에 따라 모델의 성능이 크게 좌우될 수 있습니다.
