[논문 리뷰] YOLO v1 (You Only Look Once: Unified, Real-Time Object Detection)

J Redmon. You Only Look Once: Unified, Real-Time Object Detection. CVPR 2016.

1. Introduction

  DPM은 sliding window 방식으로 전체 이미지에 classifier를 사용했다. R-CNN은 region proposal 방법을 사용하여 잠재적인 bounding box를 생성하고 여기에 classifier를 사용했다. 이처럼 기존의 object detection은 복잡한 pipeline을 가지고 있어서 각 요소를 따로 train해야만 했기 때문에 느리고 optimize하기 힘들었다.

  그러나 YOLO는 object detection을 single regression problem으로 재구성한다. 이로써 YOLO는 아주 빠르면서도 다른 real-time 시스템보다 두 배 넘는 mAP를 달성했다. 그리고 sliding window와 region proposal과는 다르게 전체 이미지를 보기 때문에, contextual 정보를 학습할 수 있다. 또한 객체의 generalizable representation을 학습하여, 새로운 도메인이나 예상치 못한 input에도 잘 대응할 수 있다.

  다만 정확도에서는 당시의 다른 SOTA 시스템에 뒤처졌다. 객체를 빠르게 식별할 수 있지만, 작은 객체를 localize하는 데에 어려움을 겪었다.

2. Grid cell, Bounding box and Confidence score

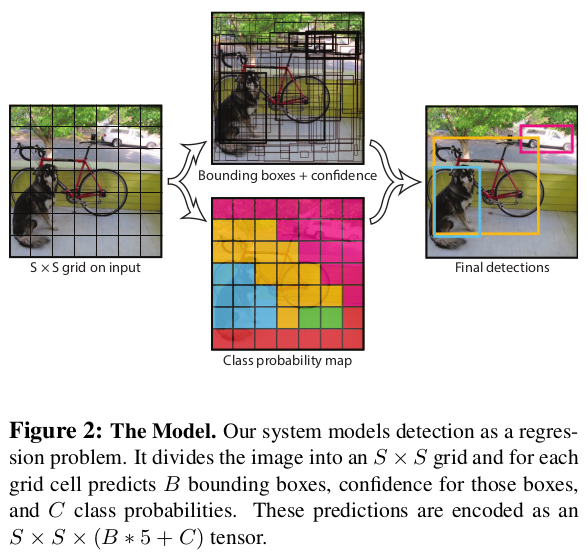
• paper에서 $S = 7, B = 2, C = 20$이다.

• input 이미지를 $S \times S$의 grid로 나눈다. 객체의 center point가 있는 grid cell은 그 객체에 "reponsible"하다.

• 각 grid cell은 $B$개의 bounding box(bbox)와 그 box의 confidence score를 예측한다.

• 각 bbox는 $(x, y, w, h)$와 confidence score로 구성된다. $x, y$는 grid cell 내에서의 상대적인 위치로 0과 1 사이의 값이다. $w, h$는 전체 이미지 크기의 상대적인 값으로 0과 1 사이의 값이다.

• 각 grid cell은 $\mathrm{Pr(Class_\mathit{i}|Object)}$을 예측한다. bbox의 개수에 관계없이 한 번만 예측한다.

• test time에 아래 식을 이용해 각 박스별 class-specific confidence score를 구한다.

  $\mathrm{Pr(Class_\mathit{i}|Object) * Pr(Objecet) * IOU_{pred}^{truth} = Pr(Class_\mathit{i}) * IOU_{pred}^{truth}}$

3. Network Design

• 24개의 Conv layer에서 feature를 extract하고, 2개의 FC layer에서 output 확률과 좌표를 예측한다.
• 네트워크 구조는 GoogLeNet에 영감을 받았지만, GoogLeNet의 inception module을 사용하는 대신 $1 \times 1$의 reduction layer에 $3 \times 3$ conv layer가 붙은 방식을 사용했다.
  [참고: zzwon1212 - 1 x 1 Convolution and Inception Network]

4. Train

• ImageNet 1000-class competition dataset으로 20개의 Conv layer를 pretrain했다.
• 여기에 4개의 Conv layer와 FC layer를 추가하여 성능을 높였다.
• Detection은 미세한 visual 정보가 필요하기 때문에 input resolution을 $224 \times 224$에서 $448 \times 448$로 높였다.
• Loss는 아래 5번에서 자세히 살펴보자.
• Hyperparameter
  • Activation function: Leaky ReLu
  • Batch size: 64
  • Momentum: 0.9
  • Weight decay: 0.0005
  • Learning rate schedule
    • epoch 1: 0.001 → 0.01
    • ~ epoch 75: 0.01
    • ~ epoch 30: 0.001
    • ~ epoch 30: 0.0001
  • Dropout: 첫 번째 FC layer 뒤에서 0.5
  • Data augmentation
    • Scaling and Translation: up to 20% of the original image size
    • Exposure and Saturation: up to a factor of 1.5 in the HSV color space

5. Loss function

5.1. $\lambda_{coord} = 5$, $\lambda_{noobj} = 0.5$

SSE는 localization error와 classification error에 같은 가중치를 둔다. 또한 많은 grid cell이 객체를 포함하고 있지 않기 때문에 model의 학습이 불안정해지게 된다. 이를 해결하기 위해 bounding box의 loss를 높여주고, 객체를 포함하지 않은 box의 confidence loss를 낮춰주는 가중치를 부여했다.

5.2. Localization loss: $(1), (2)$

SSE는 큰 box와 작은 box의 error도 equally weights한다. 큰 box에서의 작은 차이가 작은 box에서의 작은 차이보다 덜 중요하기 때문에 width와 height에 $\sqrt{}$를 적용하였다.

5.3. Confidence loss: $(3), (4)$

• $\mathbb{1}_{ij}^{obj}$
  cell $i$에 object(의 중심)가 존재하는 경우 → bounding box $j$가 $B$개의 box 중 가장 높은 IOU를 가지는 경우에만 1, 아닌 경우 0

• $C_i$
  cell $i$에 object가 존재하는 경우 1, 아닌 경우 0

• $\hat{C}_i$
  모델이 예측한 objectness score. 0과 1 사이의 값

• $\mathbb{1}_{ij}^{noobj}$
  cell $i$에 object(의 중심)가 존재하지 않는 경우 1, 아닌 경우 0

5.4. Classification loss: $(5)$

• $\mathbb{1}_{i}^{obj}$
  cell $i$에 object(의 중심)가 존재하는 경우 1, 아닌 경우 0

• $p_i(c)$
  cell $i$에 클래스 $c$가 존재하는 경우 1, 아닌 경우 0

• $\hat{p}_i(c)$
  cell $i$에 클래스 $c$가 존재할 것으로 예측한 확률

• classification의 loss로는 보통 cross entropy를 사용하지만 YOLO에서는 regression에서 사용되는 SSE를 사용했다. 논문에서 언급한 아래 부분과 일맥상통하다.?

  We reframe object detection as a single regression problem, straight from image pixels to bounding box coordinates and class probabilities.

6. Inference

• YOLO는 다른 classifier-based 방법들과 달리 하나의 네트워크 evaluation만 필요하기 때문에 test time에서 굉장히 빠르다.

• 이미지에서 98개의 bbox와 각 bbox마다 class prob을 예측한다.

• Nonmax suppresion으로 threshold 미만의 bbox들을 제거하고, 한 객체에 대해 겹치는 여러 bbox 중 최적의 bbox만을 남긴다.
  [참고: zzwon1212 - Object Detection 3.5. Nonmax Suppression]

7. Limitations

• 각 grid cell이 두 개의 bbox와 하나의 클래스만을 예측할 수 있다는 큰 한계를 가진다. 특히 새떼와 같이 작은 객체가 무리지어 나타날 때 이러한 한계가 명확하다.

• 새롭거나 unusal한 비율의 객체를 어려워한다.

• 상대적으로 coarse한 feature를 사용하기 때문에 작은 객체나 세부적인 패턴을 예측하기 어려울 수 있다.

• 작은 bbox의 error는 IOU에 큰 영향을 미치지만, YOLO는 작은 bbox의 error와 큰 bbox의 error를 똑같이 처리한다. (Loss에서 w와 h에 sqrt를 적용하여 감쇄하는 것 아닌가?)