0. 들어가며
-
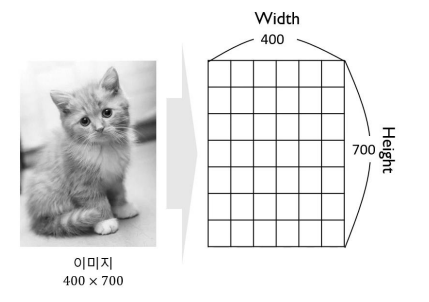
흑백 이미지는 2차원의 행렬(Width, Height)로 표현할 수 있다.
-
행렬은 흑백의 톤(짙고 엷은 정도)을 실수 값으로 표현
-
8bit: 1~256 / 16bit: 1~65536
-
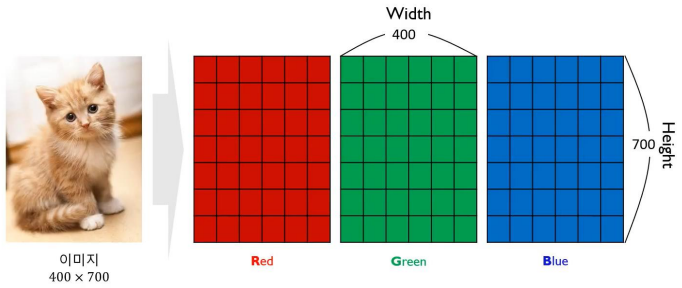
컬러 이미지는 3차원의 Tensor로 표현됨: Width, Height, RGB
-
각각의 행렬은 색의 톤을 실수 값으로 표현
-
8bit: 1~256 / 16bit: 1~65536
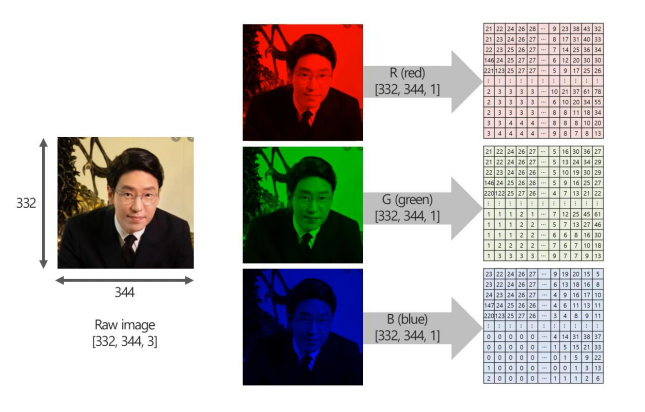
예를 들어 우리가 흔히 보는 모든 이미지나 비디오 데이터는 위 사진처럼 RGB의 픽셀값들로 나타낼 수 있다.

Red의 이미지를 확대하면 각각의 픽셀 값을 알 수 있다.
1. Convolution Neural Networks (CNN)
0. Background of CNN
-
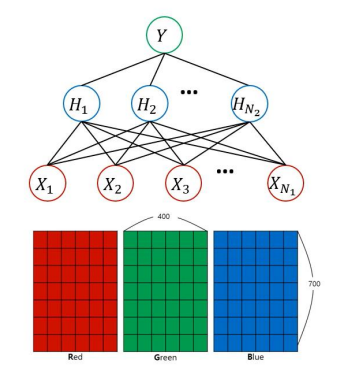
각각의 픽셀을 하나의 변수로 간주하여 모델링
-
N1 = 400(width) x 700(height) x 3(RGB) = 840,000개
-
N2의 크기도 변수의 수에 맞춰서 정함 ->
(840,000 x N2) 파라미터 ->
Input layer와 hidden layer 사이에 너무 많은 가중치 -> 학습이 어렵다!
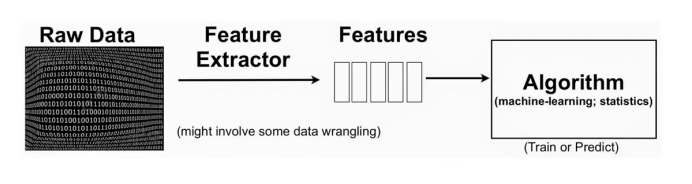
기존에는 변수가 많아서 학습이 어려웠을 때의 방안은 아래와 같았다.
- 변수의 수를 줄이기 위해 low level 변수(픽셀)를 조합하여 보다 적은 수의 변수를 생성
- Feature engineering: 도메인 지식, 기계학습, transform 기법을 이용하여 feature 생성

이미지 데이터는 아래와 같은 특징이 있다.
-
이미지의 경우 인접 변수(픽셀)간 높은 상관관계를 가짐 (
Spatially-Local Correlation) -
이미지의 부분적 특성 (e.g, 눈, 귀)은 고정된 위치에 등장하지 않음 (
Invariant Feature)
그렇다면 이러한 이미지 데이터의 특성을 반영하여 모델을 구성하면 성능이 더 좋아지지 않을까?
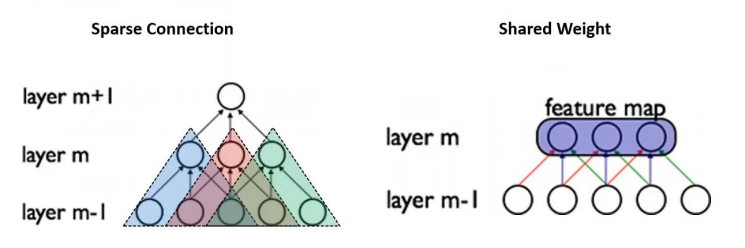
-
Spatially-local correlation을 고려하기 위하여Sparse Connection구성 -
Invariant feature를 추출하기 위해Shared Weight개념 이용 -
위의 둘을 실현시킨 방법이
Convolution
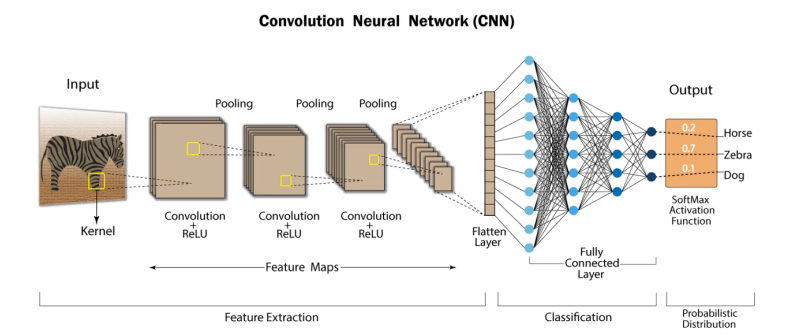
CNN이란?
- 이미지 데이터의 특성을 잘 반영할 수 있는 인공신경망 모델
- 2D 혹은 3D구조를 유지하면서 학습
- 일반적인 CNN은
Convolution연산,Activation연산,Pooling연산의 반복으로 구성됨
- 일정 횟수 이상의 Feature Learning 과정 이후에는
Flatten과정을 통해 이미지가 1차원의 벡터로 변환됨
1. Convolution
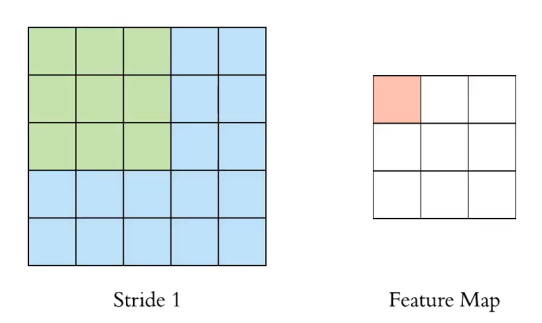
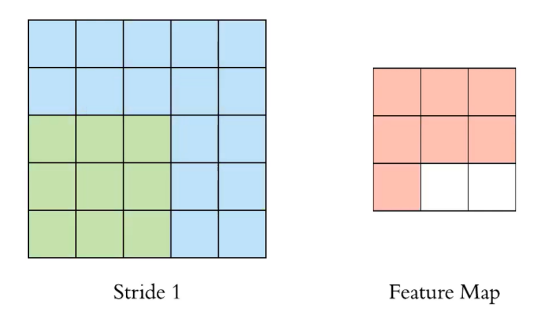
위 사진은 stride를 1로 하여 3x3 Filter를 Convolution하는 과정이다. stride란 필터의 적용 위치 간격이다.
Convolution 결과 3x3의 Feature Map이 나온 것을 확인할 수 있다.
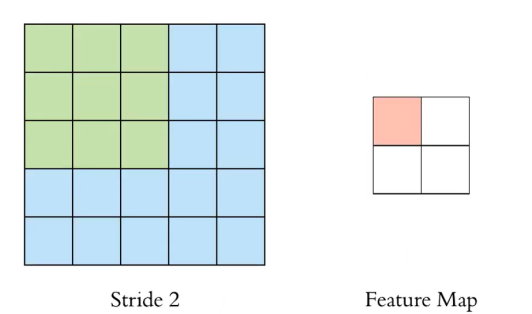
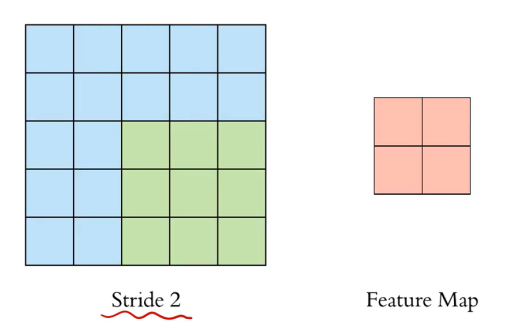
위 사진은 stride를 2로 하여 3x3 Filter를 Convolution하는 과정이다.
이번에는 처음과 다르게 Convolution 결과가 2x2의 Feature Map이 나온 것을 확인할 수 있다.
stride를 크게 하는 것은 이미지의 특징을 놓칠 가능성이 증가하고, 이는 성능 악화로 이어질 수 있다는 단점이 있다.
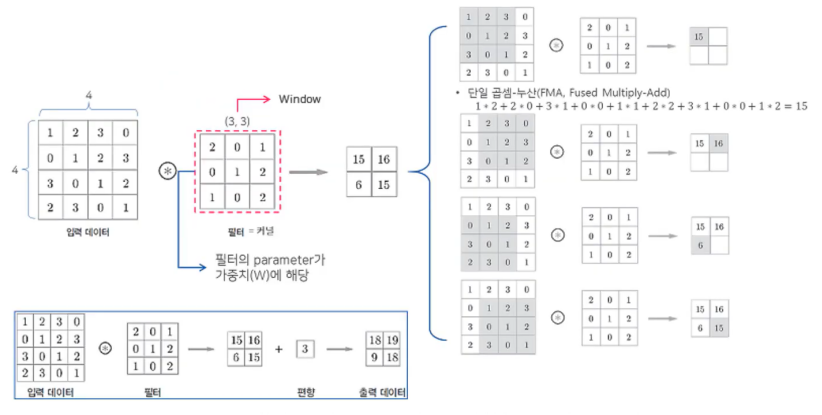
위 사진은 4x4 이미지 데이터와 3x3 filter를 Convolution하는 과정의 다른 예시이다.
2. Activation
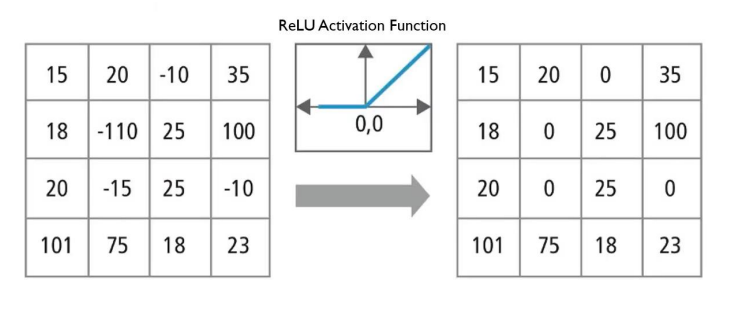
-
Convolution을 통해 학습된 값들의 비선형 변환 -
ReLU를 주로 사용
3. Padding
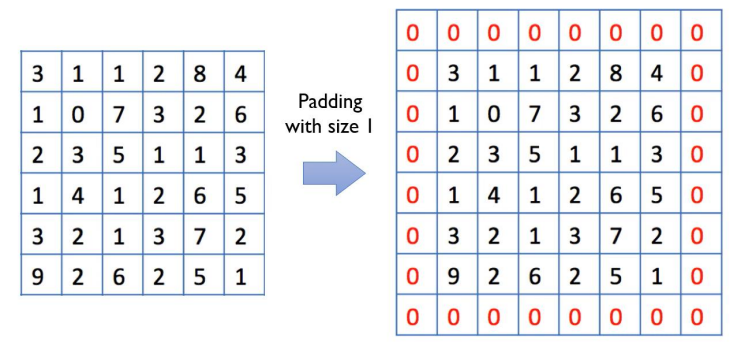
-
Convolution결과 이미지가 입력 이미지의 크기와 같으면 편리할 때가 많음 -
가장자리에 있는 픽셀들은 중앙에 위치한 픽셀들에 비하여
Convolution연산이 적게 수행됨 -
이를 위한 해결책으로 원 이미지 테두리에 0의 값을 갖는 픽셀 추가
-
테두리에 추가된 0값의 픽셀 -> Pad, 테두리에 추가된 0값의 픽셀 추가 ->
Zero Padding
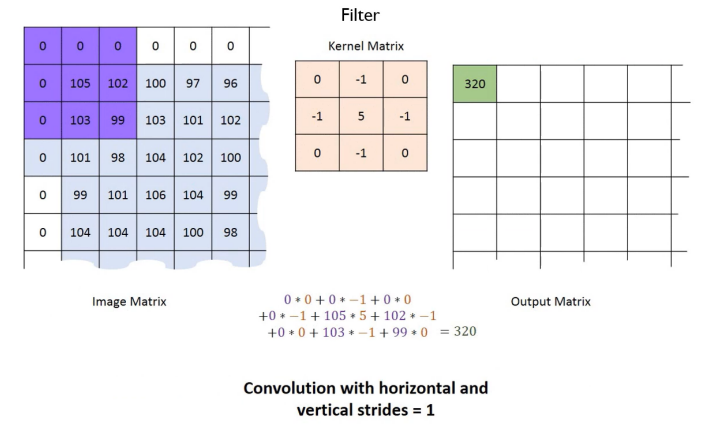
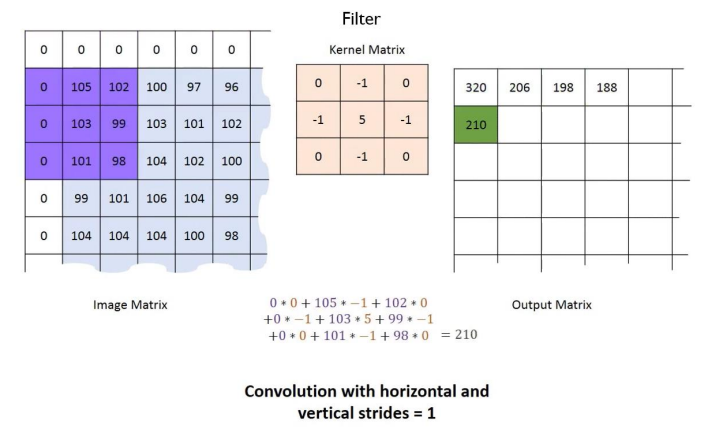
Zero-padding, 1 stride를 적용한 Convolution 연산 예제이다.
위 그림을 보면 가장자리에 위치한 픽셀들의 데이터를 균등하게 반영함을 알 수 있다.
4. Pooling
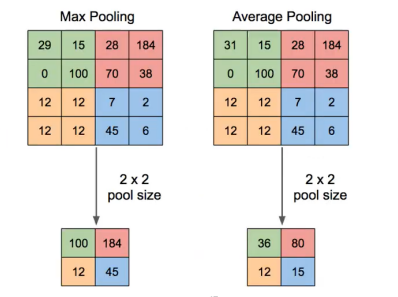
-
Feature Map의 공간적 크기를 줄이자
-
일정 영역의 정보를 축약 ->
Pooling -
Max Pooling,Average Pooling(이미지 분석에서는 주로Max Pooling) -
Pooling window 크기: 주로 Stride값과 동일하게 설정
-
Pooling 층의 유닛에도 활성화 함수를 적용하는 것은 이론적으로 가능 -> 보통은 적용 X
-
Pooling 시 padding은 보통 사용 X
5. Flattening
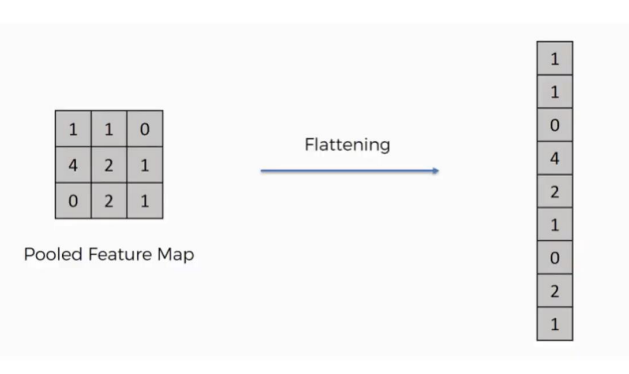
- 2차원, 3차원의 행렬/텐서 구조를 1차원의 벡터로 변환 ->
Flattening
6. 출력크기 계산
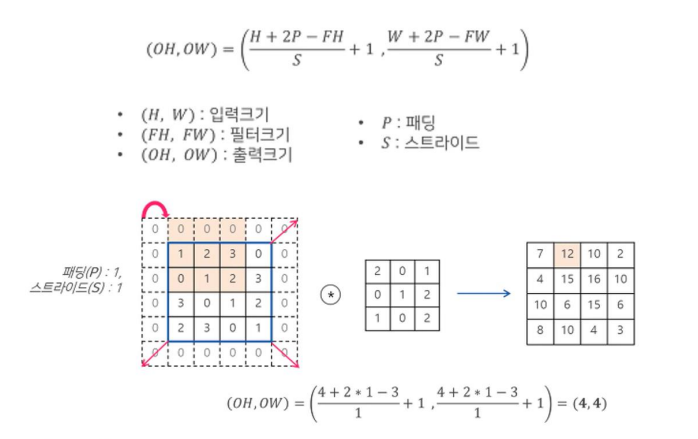
위의 식은 암기할 필요없이 식과 예제를 보며 이해하기만 하면 된다.
7. CNN의 하이퍼파라미터
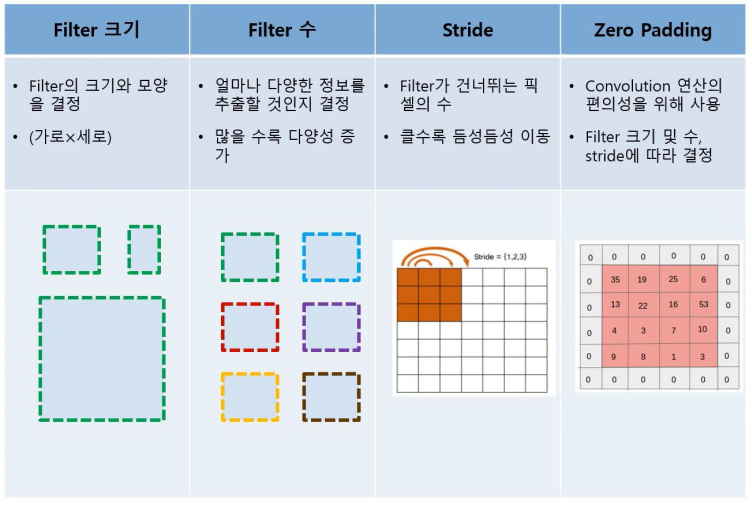
2. CNN 구조
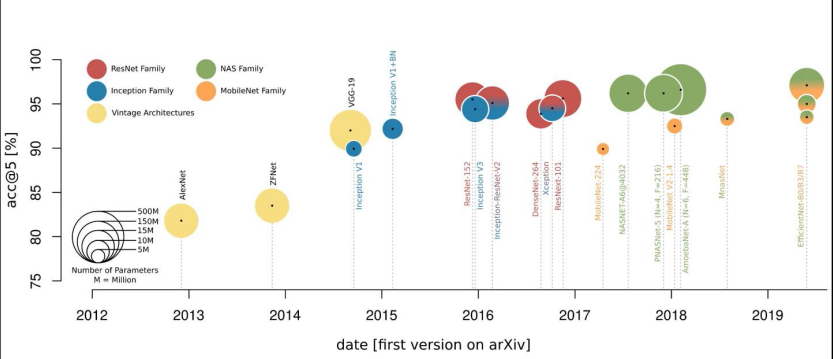
0. CNN 발전과정
1. AlexNet
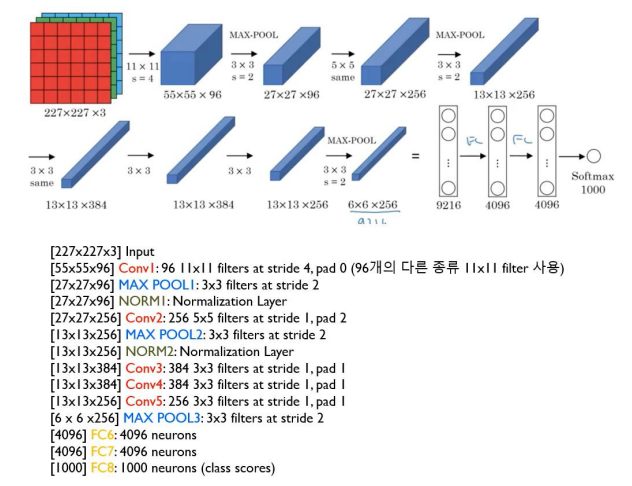
cf) Filter의 개수 = Output 채널의 개수
2. ZFNet
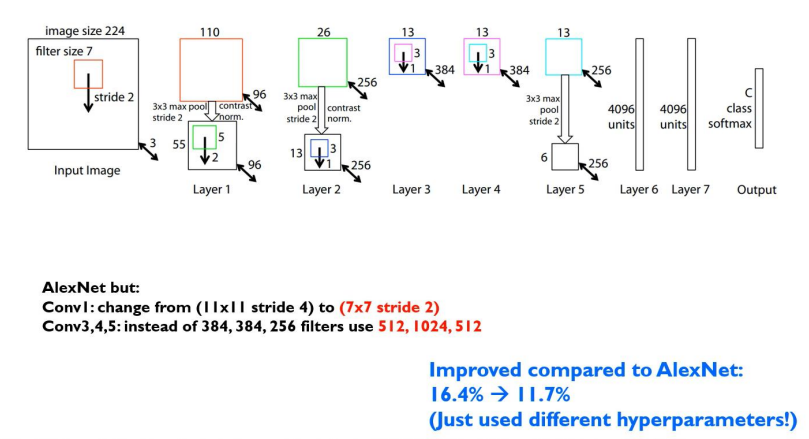
AlexNet과 거의 유사하게 동작하지만 차이점이 2가지 존재한다.
3. VGG
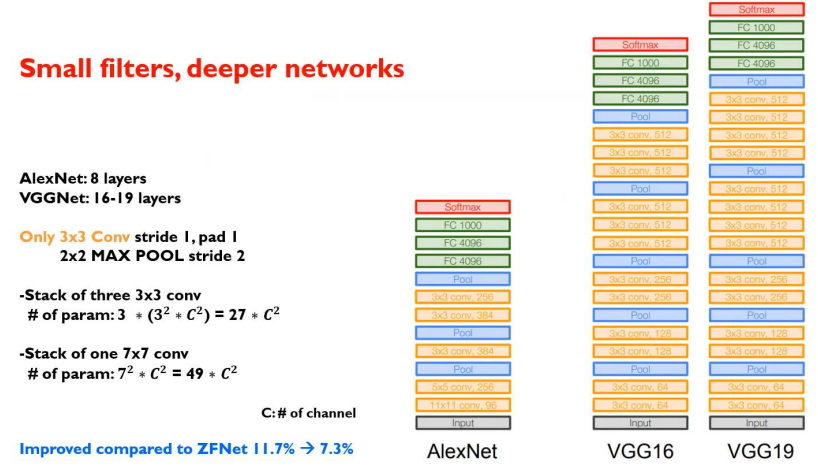
4. GoogLeNet
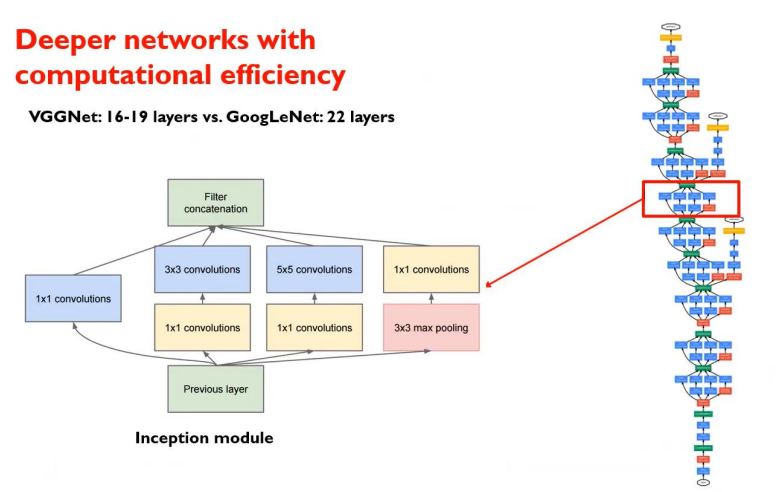
다른 CNN 모델들과 GoogLeNet 모델의 가장 큰 차이점은 1x1 convolution 과정을 사전에 한 번씩 거친다는 점이다.
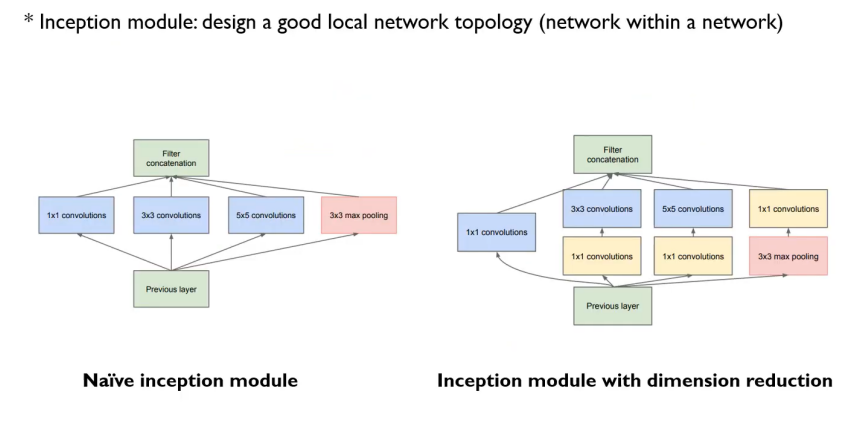
GoogLeNet 모델에서의 inception module은 1x1 convolution 과정을 거치는데 이는 중요한 역할을 한다.
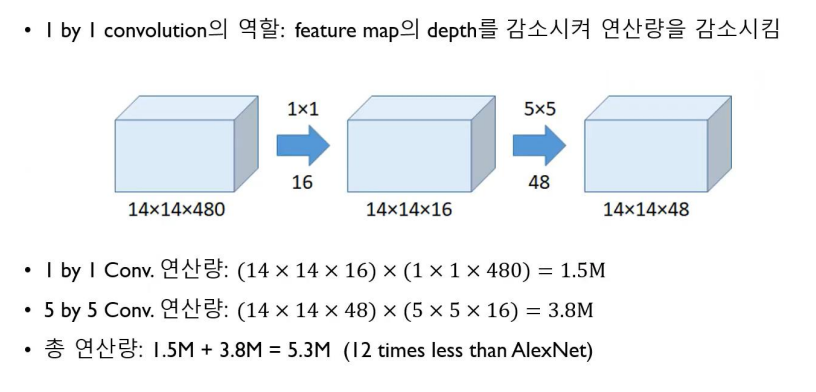
위 그림을 보면, 1x1 convolution 과정을 진행한 후 연산량을 계산하면 약 5.3M이 나온다.
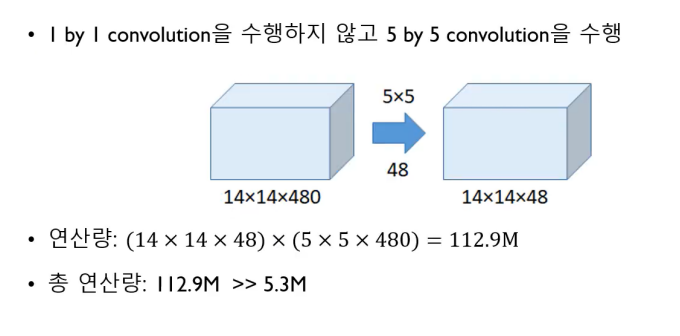
1x1 convolution 과정을 진행하지 않았을 때의 계산량은 112.9M으로 1x1 convolution 과정을 진행하면 연산량이 몇십배가 줄어듬을 확인할 수 있다.
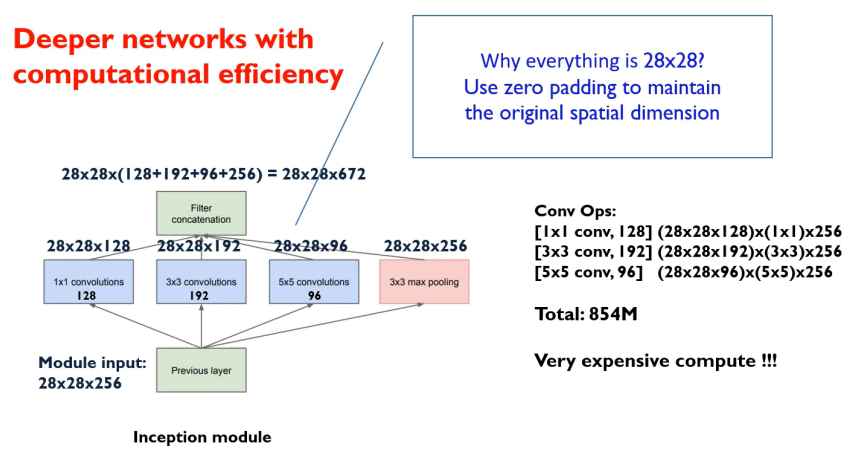
1x1 convolution 과정을 진행하지 않고 연산을 했을 때 854M의 연산량이 도출됨을 알 수 있다.
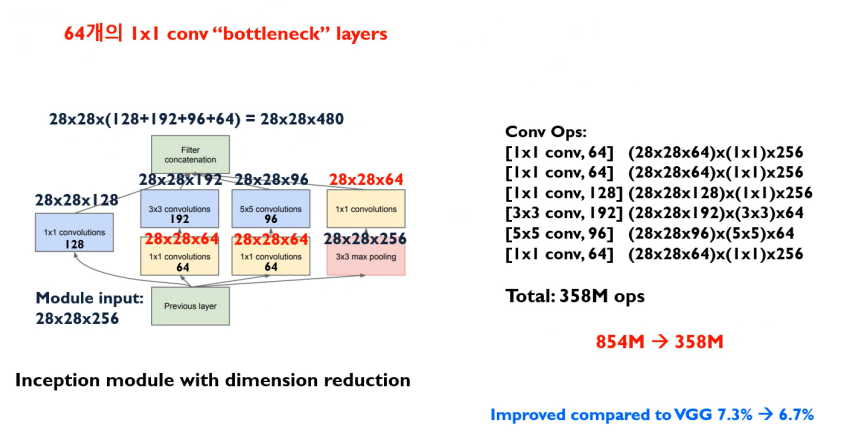
그러나 1x1 convolution 과정을 진행하고 연산을 한다면 358M의 연산량으로 이전 과정에 비하여 월등히 연산량이 줄었음을 알 수 있다.
5. ResNet

ResNet은 이전에 배웠던 여러 CNN모델들과 비교할 수도 없이 layer의 개수를 매우 많이 늘렸다.
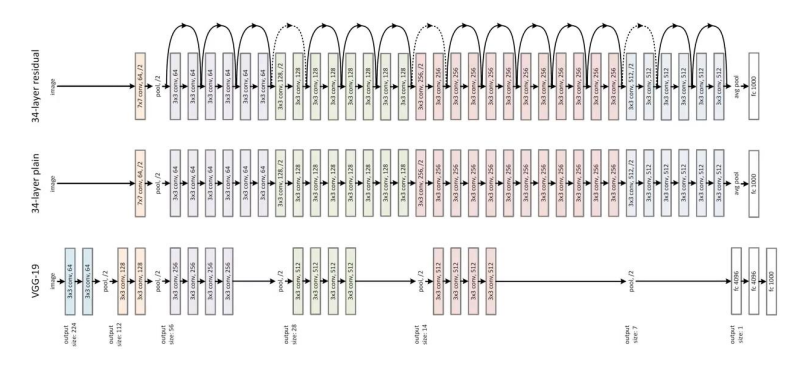
그림만 보아도 layer의 개수가 현저히 많아진 것을 확인할 수 있다.
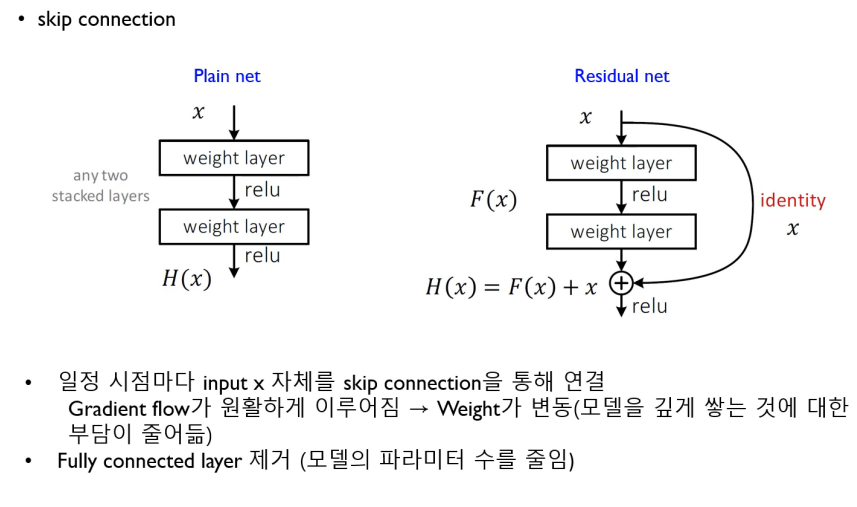
layer의 수를 늘리면 연산량이 필연적으로 많아지고, Gradient가 소실되는 문제가 발생할 수 있다.
ResNet은 이러한 문제를 해결하기 위하여 skip connection이라는 것을 도입하였다.
3. 마치며
오늘은 CNN 모델의 전체적인 과정과 흐름을 간단하게 알아보았다.
또한 필자는 고려대학교 김성범 교수님이 운영하시는 유튜브 채널을 보고 공부한 내용을 포스팅 하였으므로 아래 출처를 남긴다.
https://www.youtube.com/@user-yu5qs4ct2b
