AI&ML_Eng : [AI + ML + DL] + [DA+DS] : 선형 회귀(Linear Regression) 📈.

▽ AI&ML_Eng : [AI + ML + DL] + [DA+DS] : 선형 회귀(Linear Regression) 📈

Linear Regression.

Linear Regression 모델은 매우 간단하고, 직관적이여서, 머신러닝하면 가장 대표적으로 생각나는 모델.

• 딥러닝 교재에서 항상 1장으로 등장할만큼 기초적이고 매우 중요.

직관적 이해.

• 우리가 일상에서 “키가 클수록 몸무게가 늘어난다” 같은 경향성을 관찰할 때,
  그 관계를 직선으로 표현하는 방법이 선형회귀

• 즉, 하나의 변수(독립변수 X)가 다른 변수(종속변수 y)에 어떤 영향을 주는지를
  “직선 방정식”으로 모델링하는 것.

👉 쉽게 말해:
데이터 점들을 찍었을 때, 그 점들을 가장 잘 “가로지르는” 직선을 찾는 방법.

Linear Regression 이란?

• "Linear Regression"은 어떠한 독립 변수들과 종속 변수 간의 관계를 예측할때,
  그 사이 관계를 선형 관계(1차 함수)로 가정하고, 모델링하는 지도 학습 알고리즘.

• "Linear Regression"은 보통, 인자와 결과 간의 대략적인 관계 해석이나, 예측에 활용.

• "Linear Regression"은 확률 변수를 수학적 함수의 결과인
  변수(모델링 결과값)으로 연결해준다는데, 그 의미가 큼.
  

• "Linear Regression"은 변수의 수에 따라, 다음과 같이 구분.

  • 단순 선형 회귀 분석 : 변수 1개와 종속 변수 간의 선형 관계 모델링.
  • 다중 선형 회귀 분석 : 독립 변수 여러 개와 종속 변수 간의 선형 관계 모델링.
  • 단순 선형 회귀 분석은 Visualization이 쉽고(2차원 공간에서 선형 함수로 표현 가능),
    변수가 하나여서 이해가 쉽지만,
  • 실생활에서의 문제들은 보통 '다중 선형 회귀 문제'인 경우가 대다수.

• "종속 변수" == 우리가 예측하고 싶은 값 ( ex: 집 가격, 시험 점수, 매출 등등)

• "독립 변수들" == 예측에 쓰는 입력 요소들 ( ex: 집 면적, 방 개수, 공부 시간 등등)

• 선형 회귀는 { "입력 -> 출력 관계가 '직선 형태'일 것} 라는 가정을 세우는 것.

• 가령 𝑦 =𝛽0+𝛽1x 처럼 1차 함수 형태로 예측.

선형 회귀 방정식.

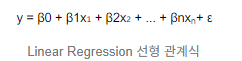
y: 종속 변수, βk :회귀 계수, Xk:독립 변수, ε: 오차항(모델으로 설명할 수 없는 부분),
식에 X1까지만 존재한다면, 단순 선형 회귀 분석의 식.

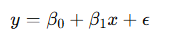
• y: 예측값(종속변수)
• x: 입력값(독립변수)
• β0: 절편(intercept, y축과 만나는 점)
• β1: 기울기(slope, x가 1 증가할 때 y가 얼마나 변하는가)
• ϵ: 오차(error, 데이터가 직선에 완전히 맞아떨어지지 않는 차이)

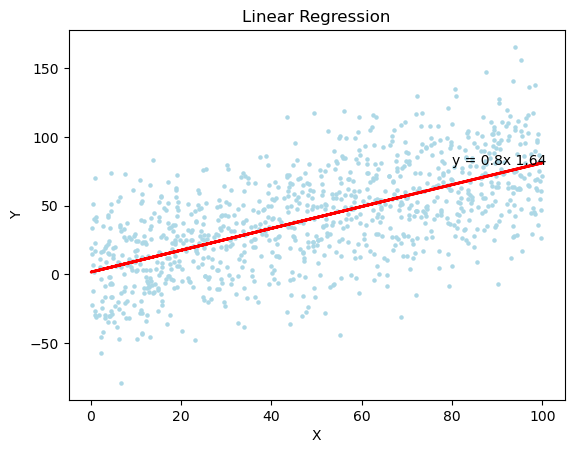
"가장 잘 맞는 직선"이란?

• 데이터들을 그래프상에 표기했을 때, 여기를 지나치는 직선은 무수히 많음.

• 이 중 어떤 직선을 선택해야 할까?? -> "오차(정확히는 잔차)가 최소가 되는 직선"을 선택해야 함.

오차(==잔차)를 수치로 정의해야 하는데, 보통은 "제곱 오차합(SSE : Sum of Squared Erros)을 사용.

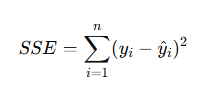
• 𝑦𝑖 : 실제 값.

• 𝑦^𝑖=𝛽0+𝛽1𝑥𝑖 : 예측 값

👉 목표: SSE를 최소화하는 𝛽0,𝛽1 찾기.
👉 이 과정을 최소제곱법(Ordinary Least Squares, OLS) 이라고 함.

• 특징 & 쓰임새:
  • 관계를 '해석'할 때 좋고 (ex: X가 1만큼 증가하면, Y가 얼마 증가할까)
  • '예측 목적으로도 사용됨'
  • 단순하고 계산이 빠르기 때문에 '기본 모델'로 많이 사용됨.

Residual (잔차) 개념 + 오차 vs 잔차.

종속 변수는 관찰의 결과인 확률변수이기 때문에, 오차(error)를 포함한다.
다만 현실적으로는 오차값을 다 파악할 수 없기 때문에 계산시에 사용하지 않고,
학습된 모델의 예측값과 실제 관측값 사이의 차이인 잔차(residual) 개념을 사용.

오차(Error, ε)

• 이론적인 개념.
• 실제 데이터가 생성될 때, 우리가 알 수 없는 "진짜 관계식"과 관측값 사이의 차이.
• 선형회귀의 '모형 가정'에서 등장하는 ε를 의미.

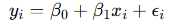
여기서 ϵi = 오차(error).

👉 문제: 이건 실제로는 절대 알 수 없음. (데이터 생성 과정 속 "진짜 노이즈")

잔차(Residual, e)

• 실제로 관측된 값과, 우리가 모델로 예측한 값의 차이.
• 데이터마다 계산 가능 !

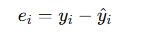
• 𝑦𝑖 : 실제 관측값

• 𝑦^𝑖 : 회귀모형으로 예측한 값

👉 이게 바로 우리가 OLS에서 사용하는 측정 가능한 오차(=잔차)

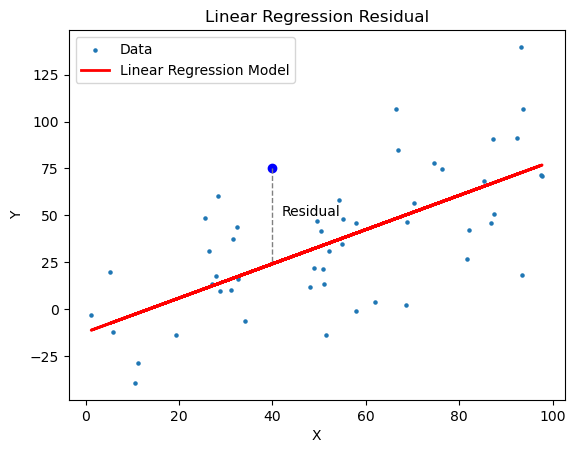
정리하자면

• 우리가 정립한 모델 { 𝑦^𝑖=𝛽0+𝛽1𝑥𝑖 } 은 실제 데이터 { 𝑦𝑖 } 와 딱 일치하지 않음

• 이 차이 𝑦𝑖−𝑦^𝑖가 잔차(e)

• 실제 모델 "오차" ( 데이터 생성 과정에서의 노이즈 )는 '이론적으로만 존재하는 개념'이라 우리가 모름.

• 따라서! 회귀 분석에서는 '잔차(e)'를 이용해서 얼마나 직선이 데이터를 잘 설명하는지 가늠.

회귀 가정 == 회귀 분석의 신뢰성을 보장해주는 조건들.

• 잔차는 정규 분포를 따른다고 가정(정규성)
• 잔차의 분산이 일정해야 한다 (등분산성)
• 잔차들끼리는 서로 독립적( 자기 상관이 없음)

제곱 잔차 (Squared Error)

• 잔차 값을 그냥 합치게 되면, 문제가 발생함.

  • 어떤 값은 '양수', 어떤 값은 '음수' -> 그냥 더하면 상쇄되어 "0"이 될 수 있음.

👉 그래서 오차를 제곱해서 모두 양수로 만듦.

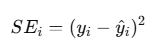
제곱 잔차 합 ( SSE : Sum of Squared Erros )

• 모든 데이터에 대해 "제곱 오차를 합한 것"

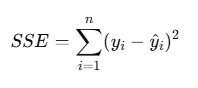
• 𝑛: 데이터 개수

• 𝑦𝑖: 실제값

• 𝑦^𝑖=𝛽0+𝛽1𝑥𝑖: 예측값(직선으로 나온 값)

즉, SSE는 직선이 데이터에 얼마나 잘 맞는지 측정하는 지표.
👉 값이 작을수록 직선이 데이터에 더 잘 맞는다는 뜻!

정리하자면

• 표에 흩뿌려진 데이터 점들이 있고, 직선을 하나 연결한다고 생각을 해보면
• 각 점에서 직선까지의 '세로 거리'가 잔차
• 그 거리들을 제곱해서 다 합친 것이 SSE.

📉 목표: SSE가 가장 작아지도록 직선
(즉, 𝛽0,𝛽1)을 찾는 것.

• 이 방법이 바로 최소제곱법 (OLS: Ordinary Least Squares).

Ex)

• 데이터가 2개 있다고 가정해봅시다.

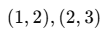
직선이 𝑦^=𝑥라고 하면:

x=1일 때 예측값 = 1 → 실제값=2 → 오차=1 → 제곱=1

x=2일 때 예측값 = 2 → 실제값=3 → 오차=1 → 제곱=1

👉 SSE = 1+1=2

만약 더 잘 맞는 직선이 존재한다면, SSE는 더 작아지게 됨.

최소제곱법 (OLS)과 잔차제곱합(SSE)

SSE(Sum of Squared Erros, 잔차 제곱합)

• 실제 관측값과 모델이 예측한 값 사이의 "잔차(residual) 제곱합"

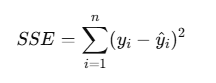
• 용도.
  • 모델이 데이터를 얼마나 잘 설명하는지 평가
  • 잔차가 작으면 직선이 데이터에 잘 맞음.
• 쉽게 말하면 : "좋은 직선을 평가하는 점수표"

SSE를 쓰는 이유.

• 잔차(residual) = 실제값 − 예측값

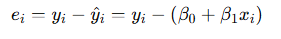
① 단순 합의 문제.

• 그냥 잔차를 모두 더하면 :

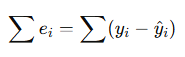
+, −가 섞이면 서로 상쇄될 수 있음

예: +3, −3 → 합하면 0인데 실제 오차는 큰데 무시됨

② 절댓값 문제.

∑∣ei∣를 사용하면 음수 문제는 해결됨.

• 그러나 ∣x∣는 0에서 미분 불연속 → 수학적으로 편미분으로 풀기 어려움.

③ 제곱의 장점.

∑ei2​=∑(yi​−y^​i​)2

• 항상 양수 → 오차 크기 반영

• 큰 오차를 더 강조 (제곱 효과)

• 미분 가능 → 최적화(미분=0)로 해를 쉽게 구함

OLS (Ordinary Least Squares, 최소 제곱법)

• 'SSE'를 '최소화'하도록 회귀 계수(𝛽0,𝛽1)를 찾는 방법/규칙.

• 용도

  • 직선을 그릴 때 "SSE가 가장 작도록" 기울기와 절편을 계산
  • 실제 선형회귀 학습 과정에서 사용하는 핵심 원리

• 쉽게 말하면, "점수표(SSE)를 가장 좋게 만드는 전략/방법"

관계 정리

• SSE: 직선이 데이터를 얼마나 잘 맞추는지 계산하는 값(숫자,평가 지표)
• OLS : 그 SSE를 '최소로 만드는 직선'을 찾는 방법.

최소제곱법 (OLS) + 회귀 계수

목표

• OLS의 목표는 '잔차 제곱합(SSE)'을 최소화하는 직선을 찾는 것.

• 직선의 식은 : y^​=β0​+β1​x

여기서

• β0: 직선의 시작점(절편, y축과 만나는 지점)
• β1: 직선의 기울기

👉 목표: 데이터와 직선의 차이가 최소가 되도록 𝛽0,𝛽1을 정한다.

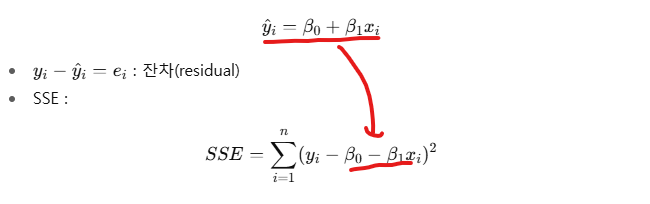
잔차와 SSE.

• 각 점마다 실제값 𝑦𝑖와 예측값 𝑦^𝑖 의 차이를 잔차(residual) 라고 한다.

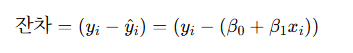
• 이 잔차들을 제곱해서 모두 더한 값이 SSE (Sum of Squared Errors).

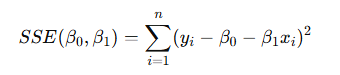
👉 OLS(최소제곱법)는 이 SSE를 최소화하는 𝛽0,𝛽1을 찾는 방법.

SSE 최소화 조건 (편미분).

SSE는 𝛽0,𝛽1이라는 두 개의 변수에 대한 함수.

• 👉 따라서 SSE를 최소로 만들려면, 두 변수에 대해 편미분 후 0으로 놓는다.

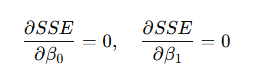
이렇게 두 개의 식을 얻을 수 있음. (이를 정규방정식(Normal Equation) 이라고 부른다.)

(1) 𝛽0 에 대한 편미분.

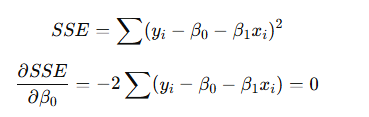
• 정리하면

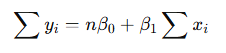
(2) 𝛽1 에 대한 편미분.

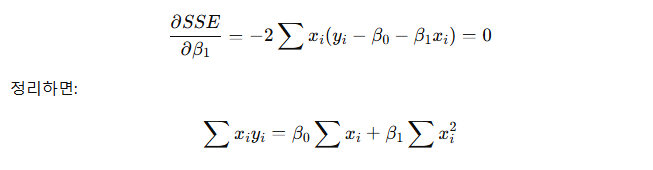
동시에 풀면

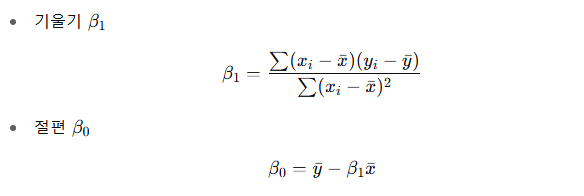
👉 여기서 𝑥ˉ,𝑦ˉ 는 각각 x와 y의 평균.

직관적 이해.

• β1 공식의 분자: x와 y가 얼마나 같이 움직이는가? (공분산)

• 𝛽1공식의 분모: x 자체가 얼마나 퍼져 있는가? (분산)

• 즉, x가 1만큼 변할 때 y가 평균적으로 얼마나 변하는지 보여준다.

• 𝛽0는 단순히 평균점을 직선 위에 맞추기 위해 계산되는 값

다중 선형 회귀 (Multiple Linear Regression)

기본 개념.

• 단순 회귀: 설명변수가 1개일 때

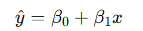
• 다중 회귀: 설명변수가 여러 개일 때

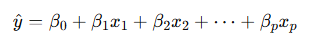
👉 여기서 𝑥1,𝑥2,⋯,𝑥𝑝는 독립 변수들, 𝛽0,𝛽1,⋯,𝛽𝑝가 우리가 찾고 싶은 회귀 계수.

행렬로 표현하기.

• 다중 회귀는 행렬(벡터)로 쓰면 훨씬 깔끔.

  • 입력 데이터 행렬 (n × (p+1))

    

    • (맨 앞의 1은 절편 𝛽0을 위한 상수항)

  • 계수 벡터
    

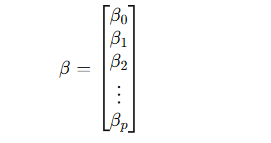
  • 실제값 벡터
    

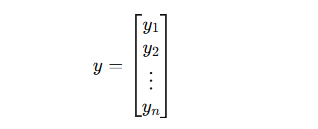
👉 모델 식은

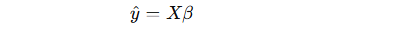
최소제곱법(OLS) 목적 함수.

단순 회귀 때와 마찬가지로, 잔차 제곱합(SSE) 을 최소화해야 함.

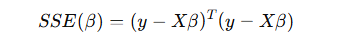
편미분 후 최적해 구하기.

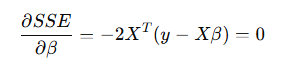
정리하자면

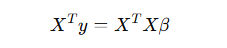
👉 이게 바로 정규방정식(Normal Equation)

다중 회귀 계수 공식.

위 식을 풀면, OLS 해는 다음과 같음 :

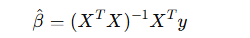
• 여기서 (𝑋𝑇𝑋)−1는 역행렬 (데이터가 선형 독립일 때만 존재)

• 이 공식을 이용하면 회귀 계수를 한 번에 벡터로 구할 수 있다.

단순 회귀와 비교.

직관적 의미