AI&MLEng : 이론 공부 : 통계를 위한 확률 다루기 기초 확률이란? : 01. 경우의 수.

▽AI&MLEng : 이론 공부 : 통계를 위한 확률 다루기 기초 확률이란? : 01. 경우의 수.
목 차
1. 곱의 법칙.
2. 합의 법칙
3. 순열(Permutations)
4. 중복 순열 (Permutations with Repetitions or Product)
5. 조합 (Combinations)
6. 중복 조합 (Combinations with Repetitions)
7. 중복된 원소를 갖는 순열(Permutation of Multisets)
8. 원순열(Circular Permutation)

경우의 수는 (말 그대로) 일어날 가능성이 있는 '경우(상황)'의 총 개수.
경우의 수를 계산하는 방법은 상황에 따라 다양.
1. 곱의 법칙.(Product rule / 곱셈법칙)
상호 독립적인 사건(한 사건의 발생이 다른 사건의 발생에 영향을 주지 않는 경우 : ex 동전을 두번 던진다고 가정할 때 첫번째 던짐과 두번째 던짐의 확률은 서로 독립적.)의 경우, 각 사건이 발생할 수 있는 경우의 수를 곱하여 전체 경우의 수를 계산.
ex) 한 자리 수로 이루어진 3자리 수를 만들 때, 각 자리마다 가능한 경우의 수는 10가지 이므로,
총 경우의 수 : 10 x 10 x 10 = 1000가지.
정의(직관)
- 서로 독립적으로 선택해야 하는 단계들이 있을 때, 각 단계의 가능한 경우 수를 곱하면 전체 경우의 수를 구할 수 있음.
ex) 상의(3종류) × 하의(2종류) = 전체 옷차림 경우 수 3 × 2 = 6.
수식.
- 단계 1에 a가지, 단계 2에 b가지, ..., 단계 k에 z가지가 있다면 전체 경우 수는
𝑎×𝑏×⋯×𝑧
간단 예제.
- PIN 코드(숫자 0~9 중에서 3자리, 중복 허용): 각 자리마다 10가지
→ 10 x 10 x 10 = 1000
AI/ML에 적용되는 경우
-
그리드 서치(grid search) : 하이퍼파라미터의 각 선택지들을 곱해서 총 실험 수를 계산.
-
데이터 증강 단계(랜덤 회전 5가지 × 색상 변환 4가지 × 크롭 3가지) → 총 경우 수 = 5×4×3.

2. 합의 법칙 (Sum rule / 덧셈법칙)
정의(직관)
- 서로 배타적(mutually exclusive)인 선택지들(서로 겹치지 않는 집합들)이 있을 때, 각 집합의 경우 수를 더하면 전체 경우 수를 구할 수 있음.
ex) A 이벤트(3가지) 또는 B 이벤트(4가지)를 택하는 경우 → 전체 : 3+4=7
- 주의 : 겹치는 경우(교집합)가 있으면, 단순 합으로는 안되고, 중복으로 카운팅 한 것을 빼줘야 함. (포함-배제 원리)
수식.
- 단계 1에 a가지, 단계 2에 b가지, ..., 단계 k에 z가지가 있다면 전체 경우 수는
𝑎×𝑏×⋯×𝑧
간단 예제.
- 동시 배타적 : 붉은 모자 3종류 또는 파란 모자 2종류 -> 3+2 =5
- 겹칩이 있는 경우 : 집합 A(5개), 집합B(4개), 교집합(1개) -> 5+4-1 = 8
AI/ML에 적용되는 경우
-
분류 문제에서 사건 A 또는 B의 확률 계산(단, 배타성 확인 필요).
-
파이프라인에서 'A 방식으로 처리하거나 B 방식으로 처리' 같은 분기(branch) 경우 수 계산.

3. 순열 (Permutations) — 순서가 중요할 때
특정 집합에서 중복을 허용(비복원 추출)하지않고 일부 원소를 선택하여 '순서에 맞게' 나열하는 방법을 다루는 개념.
- 선택된 원소들의 순서가 중요한 경우에 사용.
- 주로 "n 개 중에서 r 개를 선택하여 나열하는 경우의 수"를 계산하는 데 사용.
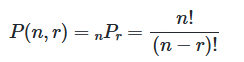
정의(직관)
- 서로 다른 𝑛개의 원소에서 순서를 고려하여 𝑟개를 골라 일렬로 나열하는 경우의 수.
수식.
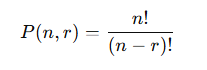
- 특히, r=n일 때 전순열 𝑛!=𝑛×𝑛−1)×⋯×1
간단 예제.
- 서로 다른 5명 중 3명을 1·2·3등으로 뽑는 경우: P(5,3)
- 계산:
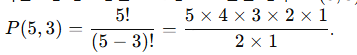
- 경우의 수는 60
응용.
-
순서가 중요한 작업(예: 경로 순서, 랭킹)
-
정렬 알고리즘/복잡도 분석에서 경우의 수 근거
-
시퀀스 생성(예: 비밀번호/토큰, 순서 있는 이벤트 나열)

4. 중복 순열 (Permutations with Repetitions / Product)
특정 집합에서 원소들에 중복을 허용(복원추출)하여 순서에 따라 나열하는 순열.
- 중복순열을 구하는 방법은 간단.
- 각각의 위치에 원소를 선택하고 나열하는 것이므로, 각 위치에 선택 가능한 원소들의 수를 곱하기.
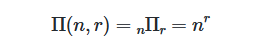
- ex: 3개의 원소 A, B, C가 있을 때, 2개의 원소를 선택하여 순서에 따라 나열하는 경우의 수는 3^2 = 9
- 가능한 순열은 AA, AB, AC, BA, BB, BC, CA, CB, CC.
정의(직관)
- 순서를 고려하지만 중복(같은 원소를 여러 번 사용)할 수 있는 경우. 길이가
𝑟인 순서열을 n종류에서 중복 허용해 만들면 경우 수는
𝑛의 𝑟제곱이다.
수식.

간단 예제.
- 숫자 0~9(총 10개)를 이용해 3자리 PIN 생성(중복 허용): 10의 3승 = 1000
AI/ML에 적용되는 경우
-
샘플 생성(복원추출 sampling with replacement)
-
무작위 초기화(여러 파라미터를 중복 선택 가능할 때 경우 수 계산)
-
문자열/토큰 시퀀스 모델에서 어휘(vocabulary) 크기^시퀀스 길이가 가능한 시퀀스 수의 상한

5. 조합 (Combinations) — 순서가 중요하지 않을 때
특정 집합에서 중복을 허용(비복원 추출)하지않고 일부 원소를 선택하여 나열하는 방법으로 순서 없이, 선택된 원소들의 조합에만 관심이 있는 경우에 사용.
- 즉 ab와 ba는 동일한 경우의 수로 취급.
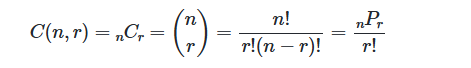
ex) 5명의 학생 중에서 3명을 선택하여 그룹을 만들 때, 가능한 경우의 수는 5 x 4 x 3/(3 x 2 x 1)로 C(5, 3) = 10로 역시 팩토리얼을 이용해 위와 같은 식으로 나타낼 수 있음.
- 조합은 다음과 같은 대칭성을 가짐.
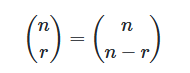
정의(직관)
- 서로 다른 𝑛개의 원소에서 순서를 무시하고 𝑘개를 고르는 방법의 수.
- 즉, 어떤 집합(부분집합)을 고르는 문제.
공식(이항계수)
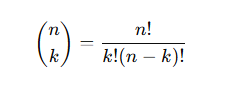
간단 예제.
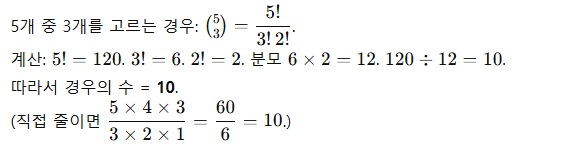
AI/ML에 적용되는 경우
-
특징 선택(feature selection): 𝑛개의 피처 중 𝑘개 조합 수 계산 → 모델 탐색의 규모 추정
-
확률(사건의 경우의 수가 동등할 때) — 동전·카드 문제 등에서 표본공간 크기 계산

6. 중복 조합 (Combinations with Repetitions)

7. 중복된 원소를 갖는 순열(Permutation of Multisets)

8. 원순열(Circular Permutation)

