[혼공머] feature engineering, 다중 회귀, Ridge, Lasso

공부 벌레가 되고 싶은 🐛 평범한 사람의 혼공머 챕터 3-3 정리 글입니다.

참고 자료

📕 교재: 혼자 공부하는 머신러닝+딥러닝
🔗 회귀 모델의 종류와 특징

다중 회귀(multiple regression)

우리가 다룰 데이터는 특성(feature) 값이 하나가 아니라 여러 개일 확률이 더 높겠죠.

이렇게 여러 개의 특성을 사용한 선형 회귀를 다중 회귀라 부릅니다.

• 다중의 독립 변수가 있는 형태 ($x_1, x_2, ...$)

• 다중회귀분석시 독립변수 간 상관관계가 높아 발생하는 다중공선성(Multicollinearity) 문제가 발생하기도 합니다.

다중공선성이 있는 경우

다중공선성이란 독립변수 간의 상관관계가 높아 발생하는 문제를 말합니다.

데이터에 다중공선성이 있는 경우, 회귀 계수의 영향력이 커져서 과다 추정될 수 있습니다.

이런 경우를 과대적합된다고 앞 글에서 설명했었습니다.

그렇다고 특성(feature)을 줄일 수도 없으니, 하는 방법이 규제(regularization)입니다.

머신러닝 모델이 훈련 세트를 너무 과하게 학습하지 못하도록 규제를 주는 것입니다.

그 방법으로는 Ridge, Lasso가 있습니다.

정리하자면 Ridge와 Lasso는 regularization을 이용한 회귀 모델링 기법입니다.

Ridge, Lasso

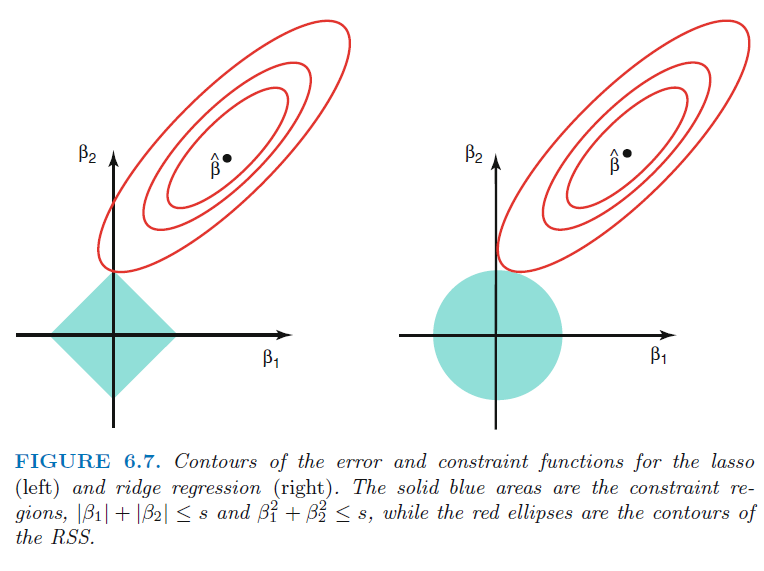
Classical linear regression: $argmin_β$ $∑ϵ^2_i$

Ridge: $argmin_β$ $ϵ^2_i+λ∑β^2_k$

Lasso: $argmin_β$ $ϵ^2_i+λ∑∥β_k∥$

맨 위의 수식은 고전적인 선형 회귀 모델이 회귀 계수를 추정할 때 사용하는 식입니다.

잔차의 제곱의 합을 계산하고 이를 비용 함수라고 부릅니다. 이 cost function이 최소가 되는 회귀 계수를 찾는 것입니다.

그런데 이제 소개할 회귀 모델은 cost function에 수식이 붙습니다. 일종의 penalty를 주는 것인데요.

말그대로 회귀 계수 값 자체가 너무 커지지 않도록 페널티를 줌으로써 회귀계수값들이 과다 추정되는 것을 막는 것입니다. 그래서 위에서는 규제(regularization)이라고도 설명했습니다.

이때 패널티 함수의 형태에 따라 ridge 와 lasso 가 구분됩니다.

• ridge regression은 회귀 계수의 제곱합을 계산하는 방식
• lasso는 회귀 계수의 절대값을 계산하는 방식입니다.

이런 페널티 함수를 이용하면 다중공선성이 있더라도 회귀 계수 과다 추정을 막을 수 있습니다.

또 더 나아가 모델이 overfitting 되는 문제도 어느 정도 완화시킬 수 있습니다.

그래서 보통 독립 변수의 개수가 데이터의 개수에 비해 너무 많은 경우에 이 기법을 사용합니다.

특히 lasso regression은 영향력이 적은 변수의 회귀 계수값을 0으로 만들기 때문에 일종의 변수 선택 효과까지 있는 장점이 있습니다.

Ridge

리지 회귀에서 가중치($w$)의 선택은 훈련 데이터를 잘 예측하기 위함 뿐만 아니라 추가 제약 조건을 만족시키기 위한 목적도 있습니다.

가중치의 절댓값을 가능한 작게 만들어 0에 가깝게 만들고 싶습니다. 이를 직관적으로 설명하면 모든 특성이 출력에 주는 영향을 최소한으로 만듭니다. (=기울기를 작게 만듦)

이런 제약을 규제(regularization)라 하였으며, 과대적합이 되지 않도록 모델을 강제로 제한합니다.

리지 회귀에서 사용하는 규제 방식을 L2 규제라고 합니다.

Ridge: $argmin_β$ $ϵ^2_i+λ∑β^2_k$

또한, 해당 식에서 λ는 매개변수를 의미합니다. 훈련 세트의 성능 대비 모델을 얼마나 단순화할지 결정합니다.

λ 값을 높일수록 패널티의 효과가 커지기 때문에 가중치가 감소하고, 작게하면 반대가 됩니다.

그래서 값을 높일 수록 계수를 0에 가깝게 만들어 훈련 세트의 성능은 나빠지지만 일반화에는 도움을 줄 수 있습니다.

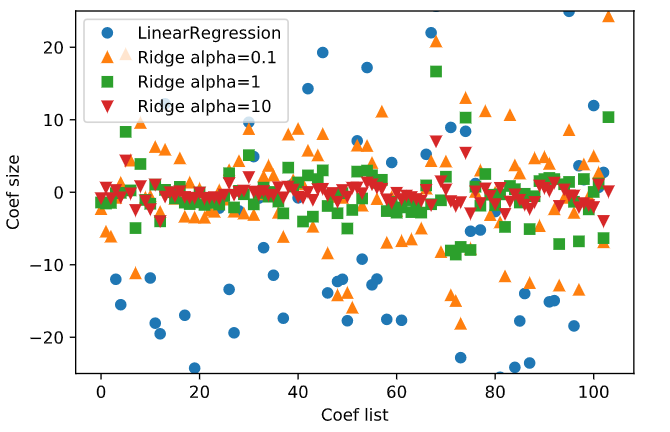
이 그림에서는 alpha를 의미하는데요. alpha 값이 클수록 더 많은 제약이 들어간 모델이므로 절대값의 크기가 작아집니다.

리지에는 규제가 적용되므로 리지의 훈련 데이터 점수가 전체적으로 선형 회귀의 훈련 데이터 점수보다 낮을 수 있습니다.

그러나 테스트 데이터 셋에는 리지의 점수가 더 높으며 작은 데이터셋에선 더 그렇습니다.

흥미로운 점은 데이터가 충분하면 규제 항의 영향력이 줄어들어서 리지 회귀와 선형 회귀가 동일한 성능을 낼 것이고,

선형 회귀의 훈련 데이터 성능이 줄어듭니다. 이는 데이터가 많아질수록 모델이 데이터를 기억하거나 과대 적합하기 어려워지기 때문입니다.

Lasso

Lasso: $argmin_β$ $ϵ^2_i+λ∑∥β_k∥$

선형 회귀에 규제를 적용하는데 Ridge의 대안으로 Lasso가 있습니다.

Ridge에 이어 Lasso도 계수를 0에 가깝게 만들려고 합니다. 하지만 방식이 조금 다릅니다. 이를 L1 규제라고 합니다. L1 Norm을 패널티로 사용하기 때문입니다.

평균제곱오차(MSE)에 $λ∑∥β_k∥$ 이 추가됩니다. 마찬가지로 λ를 크게 하면 패널티의 효과가 커져 가중치가 감소하고, 작게 하면 그 반대가 됩니다!

L1 규제의 결과로 Lasso를 사용할 때 어떤 계수는 실제로 0이 됩니다. 이 말은 모델에서 완전히 제외되는 특성이 생긴다는 뜻입니다.

이 경우는 feature selection이 자동으로 이뤄진다고 볼 수 있습니다.

일부 계수를 0으로 만들면 모델을 이해하기 쉽고, 모델의 중요한 특성이 무엇인지 드러내줍니다.

(이러한 특성이 K-NN 알고리즘에서 distance metrics를 선택할 때, 기준이 되기도 하는 것 같습니다.)

Ridge와 마찬가지로 Lasso도 계수를 얼마나 강하게 0으로 보낼지를 조절하는 alpha 매개변수를 지원합니다.

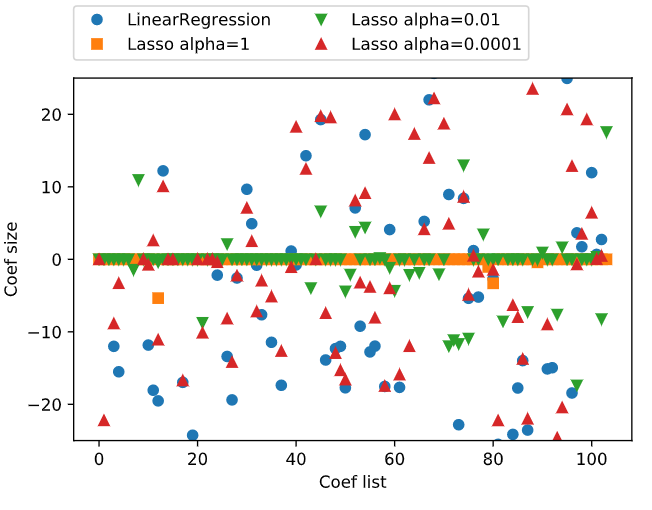
alpha 값을 낮추면 모델의 복잡도는 증가하여 훈련과 테스트셋에서 성능이 좋아집니다.

위 그림을 보면 alpha가 1일 때, 계수 대부분이 0입니다. 또한, 나머지 계수들도 크기가 작다는 것을 알 수 있습니다.

alpha가 0.0001이 되면 대부분의 계수가 0이 아닌 값을 갖게 됩니다. 규제를 덜 받았기 때문입니다.

비교를 위해 Ridge는 원모양으로 표시하였습니다. lasso alpha가 0.01일 때와 성능이 비슷하지만, 값이 0이 되지는 않습니다.

실제로 Lasso와 Ridge 두 모델 중 Ridge를 더 선호합니다. 하지만 feature가 많고 일부분만 중요하다면 Lasso가 더 좋은 선택이 될 수 있습니다.

분석하기 쉬운 모델을 원한다면 Lasso가 feature를 일부만 사용하므로 이해하기 쉬운 모델을 만들어줍니다.

feature engineering

feature engineering이란 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업을 의미합니다. 예를 들어, 집값을 예측하는 문제에서 집 면적 가로, 세로 특성이 주어졌다면 가로x세로를 통해 면적이란 새로운 feature를 만들어내는 것입니다.

정리

• 다중회귀: 여러 개의 특성을 사용하는 회귀 모델
• feature engineering: 주어진 특성을 조합하여 새로운 특성을 만드는 일련의 작업 과정
• ridge: 규제가 있는 선형 회귀 모델 중 하나, 선형 모델의 계수를 작게 만들어 과대적합을 완화 시킴
• lasso: 규제가 있는 선형 회귀 모델 중 하나, 릿지와 달리 계수 값을 아예 0으로 만들 수 있음