[혼공머] Logistic Regression(로지스틱 회귀)

공부 벌레🐛 되려다 머리가 터지려는 요즘...🤯

참고 자료

📚 교재: 혼자 공부하는 머신러닝+딥러닝
🔗 로지스틱 회귀
🔗 로지스틱 회귀분석의 원리와 장점
🔗 위키백과 - 로지스틱 회귀

저는 위 교재 흐름을 바탕으로 개념 정리 중입니다.

이번 포스팅은 챕터 4-1 로지스틱 회귀에 대한 내용입니다.

책 내용은 개념을 깊게 다루고 있진 않아서 추가적으로 정리하고 있으며, 책에 다룬 내용이 빠져 있을 수 있습니다.

로지스틱 회귀(logistic Regression)

로지스틱 회귀는 이름은 회귀이지만 분류 모델입니다. 그러므로 linear Regression과 혼동하면 안 됩니다.

선형 회귀(Linear Regression)는 범주형 변수를 예측하는 모델입니다. 파라미터 추정에 대한 포스팅은 손실 함수(loss function) 정의 해당 포스팅을 참고해주세요.

챕터 3에서는 다중선형회귀(Multiple Linear Regression)에 대해 설명했는데요.

여러 개의 특성(feature)을 사용한 선형 회귀를 다중 회귀라 불렀습니다.

즉, 다중의 독립 변수($x_1, x_2,...x_p$)와 연속형 숫자로 이루어진 종속 변수 $y$ 간의 관계입니다.

$y=β_0+β_1x_1+β_2x_2+...+β_px_p+ε$

*설명 변수의 개수가 p개인 식입니다.

다중선형회귀는 이렇게 선형적으로 표현된 관계를 가장 잘 나타낼 수 있는 회귀계수를 데이터로부터 추정하는 모델입니다.

회귀 계수는 기울기와 절편, 모델이 찾는 파라미터(parameter) 값이라 설명했습니다. (*해당 글이 이해가 안 된다면 이전 글을 차례대로 보고 오시는 것을 추천드립니다.)

책에서는 로지스틱 회귀를 통한 이진 분류와 다중 분류를 소개시켜주고 있군요. 하나씩 따라가보겠습니다.

분류 모델인 로지스틱 회귀도 다중 회귀를 위한 선형 방정식이기 때문에 확률 값으로 출력을 해야 합니다.

확률이라면 0부터 1까지의 값을 가지겠죠.

이를 도와주는 activation function이 있습니다. 바로 sigmoid function입니다.

로지스틱 함수(시그모이드 함수)

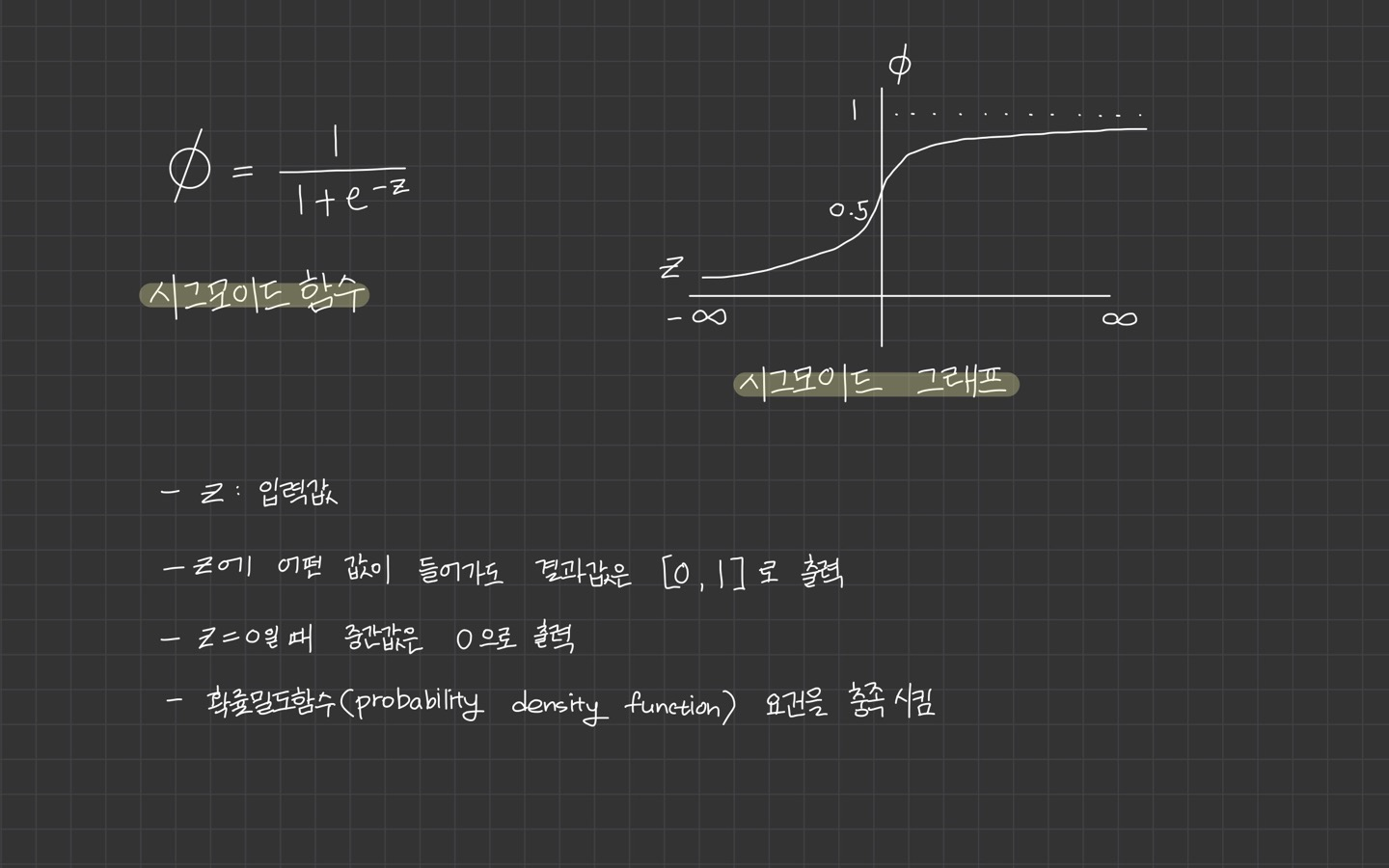
z의 값이 음의 무한대, 양의 무한대로 가까워져도 [0, 1] 사이의 값을 갖게 됩니다.

이진 분류일 경우에 0.5보다 크면 1, 0.5보다 작으면 0으로 판단합니다.

여기서 하나 추가 개념을 보고 가겠습니다❗

로지스틱은 독립 변수가 $(-∞,∞)$의 어느 숫자이든 상관 없이 종속 변수 또는 결과 값이 항상 범위 [0,1] 사이에 있습니다.

이는 오즈(odds)를 로짓(logit) 변환을 수행함으로써 얻어지는데요.

odds가 무엇일까요?

odds

odds는 승산이라고도 하며, 임의의 사건 A가 발생하지 않을 확률 대비 일어날 확률의 비율을 뜻합니다.

식은 아래와 같습니다.

$odds = \frac{P(A)}{P(A^c)}= \frac{P(A)}{1-P(A)}$

만약 $P(A)$가 1에 가까울수록 $odds$는 값이 더 커질테고, $P(A)$가 0에 가까울수록 값은 작아질 것입니다.

이렇게 두 확률의 비율을 비교하기 때문에 $y$를 odds ratio라고도 합니다.

다시 말해서, 승산이 커진다는 것은 발생할 확률이 크다는 것과 같습니다.

$P(A)$를 $x$축, 사건 $A$의 승산을 $y$축에 놓고 그래프를 그리면 아래와 같습니다.

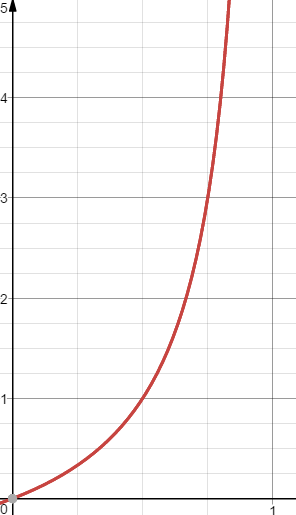
이 그래프를 보면 아까 위에서 봤던 시그모이드 함수랑 달라서 좀 당황스러울 수 있습니다.🤔

odds ratio는 독립 변수 $X$에 대하여 종속 변수 $y$가 1이 될 확률과 0이 될 확률의 비율입니다.

이 값을 그냥 선형 회귀식으로 에측하게 되면 $x$가 [0, 1]의 값을 갖게 되고, y가 $(-∞,∞)$ 값을 가지게 됩니다.

선형 회귀식: $y=β_0+βX$

왜냐하면❓ $x$가 확률이므로 [0, 1] 값을 갖게 되고 그 값을 통한 y의 값은 위 그래프처럼 나오게 되겠죠.

이 문제를 해결하기 위한 방법이 아래 방법입니다.

되게 먼길을 돌아오셨습니다. 이제 그 다음으로 넘어가겠습니다.

logit 변환

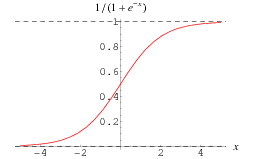
로짓 변환은 오즈에 로그를 취한 함수를 의미합니다. 입력값의 범위가 [0, 1]일 때 출력값의 범위를 $(-∞,∞)$로 변환합니다.

$logit(p) = log\frac{p}{1-p}$

이 됩니다.

로지스틱 회귀 분석의 계수 추정은 독립변수 $X$에 대한 선형 회귀식을

$X$가 주어졌을 때의 종속 변수 $Y$의 로그 오즈에 적합시킨다고 합니다.

이제 이진 분류, 다중 분류를 위한 로지스틱 회귀 내용으로 가겠습니다.

이항 로지스틱 회귀(binomial logistic regression)

종속 변수의 결과가 True, False와 같이 2개의 카테고리가 존재하는 것을 의미합니다.

범주가 두 개인 분류 문제를 풀기 위해 기존 회귀 모델을 사용 못하는 이유를 앞에서 설명했습니다.

이제 이 식이 어떻게 로지스틱 함수로 유도되는지 살펴 보겠습니다.

이항 로지스틱 회귀는 입력 벡터 $x$가 들어가면 범주 1에 속할 확률을 반환해줍니다. 그 확률값을 통해 분류를 하게 될텐데요.

위 이미지를 통해 간단히 살펴보면 결정경계(decision boundry)가 $B^Tx$의 값에 따라 달라집니다.

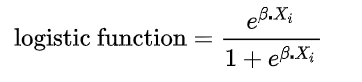
*참고 이미지

$logit(p_i) = \beta_0 + \beta_1x_i + ... + \beta_mx_{m,i} = \beta X_i$

정리하자면 회귀식 $y=β_0+βX$은 로짓 변환된 $odd$ $ratio$의 예측값입니다.

$odd$ $ratio$는 처음 알고자 했던 종속변수 $y$가 1이 될 비율을 의미합니다.

로지스틱 함수는 이것을 종속변수 $y$가 1이 될 확률로 변환하는 함수입니다. 결국 독립변수 $x$의 변화에 따른 종속 변수 $y$가 1이 될 확률을 보입니다.

또한, 로지스틱 함수와 로짓 함수는 역함수 관계입니다.

이게 neural network랑 어떻게 이어질까요?

feed-forward neural network의 FC-layer의 하나의 셀에 활성 함수(activation function)으로 sigmoid function을 쓰면 이항 로지스틱 회귀와 같아집니다.

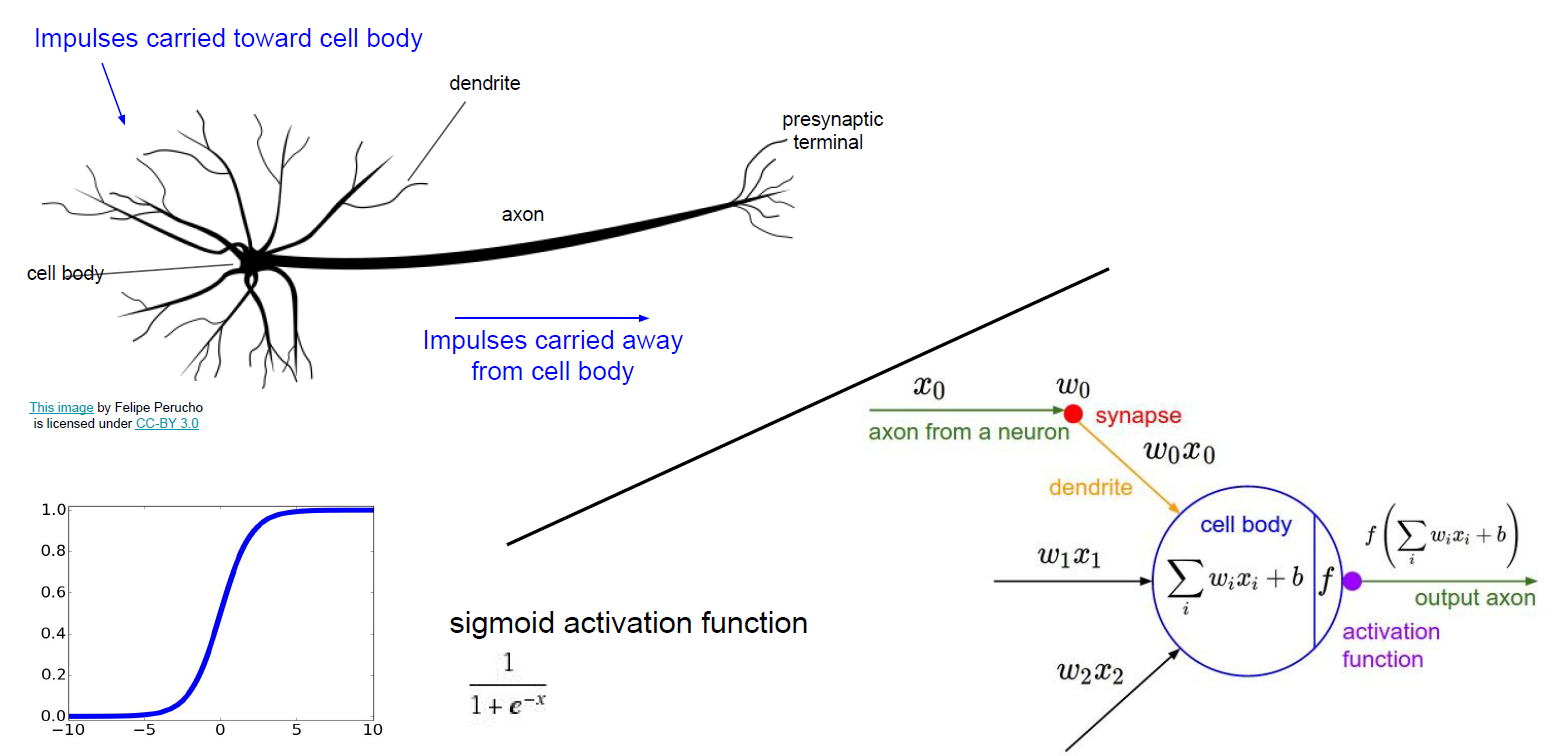
*출처: cs231n Lecture 4 Slide

다항 로지스틱 회귀

다항 로지스틱 회귀는 범주가 3개 이상인 경우에 해당합니다. 범주가 3개라고 가정하고, 이항 로지스틱 회귀 모델 두 개를 빌려와서 해결해보겠습니다.

여기서 로그승산을 활용해서 $K$개 범주를 분류하는 다항로지스틱 회귀 모델을 유도하게 되면,

위의 식에서 적었듯이 이항로지스틱 회귀모델 $K-1$개를 써서 회귀계수도 $K-1$개가 도출됩니다.

따라서 K번째 범주에 속할 확률은 이 범주에 해당하는 회귀계수 벡터 없어도 자동으로 계산되게 되며 1부터 $K-1$까지 합하는 이유입니다.

근데 $K$번째 범주에 해당하는 회귀계수 벡터를 구하고 싶답니다...🤯 그래서 또 계산을 하러... 🧮...

이번에도 어김없이 좌변에 로그를 취해줍니다. 아까 위의 로그함수 그래프를 참고하면 $x$가 0이 되는 지점의 확률을 제외하고 확률은 승산보다 작습니다.

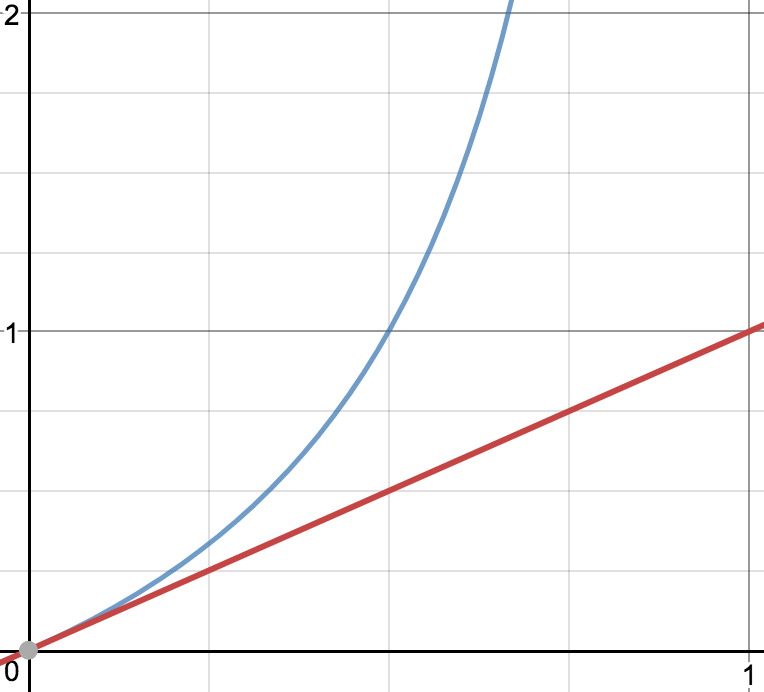
*참고 이미지

위 이미지를 참고하면 확률이 승산($\frac{x}{(1−x) }$)보다 작습니다.

*해당 식 유도 과정은 위키백과와 래츠고 블로그를 참고했습니다.

식의 마지막에 추가적으로 ${\displaystyle -lnZ}$ 항과 함께,

형 예측 변수로서 관련된 확률이 로그 형태로 나타나 있습니다.

이 항은 결과가 확률 분포가 되도록 정규화 인자로서 작용하며 양변을 지수화함으로써 나타낼 수 있습니다.

Z가 정리되고 다시 식에 대입했을 때 최종적으로 나온 $P(Y=c)$는 소프트 맥스 함수와 정확히 일치합니다.

이 식에 이항 로지스틱 회귀 모델처럼 0과 1을 대입하면 식이 똑같이 정리됩니다.

여기서 $Z$의 용도는 결과를 $y_i$에 대한 확률분포가 되도록 만드는 것입니다.(총합이 1이 되도록)

$Z$는 단순히 비정규화 확률의 총합이며, 그 확률을 $Z$로 나눔으로서 정규화 확률이 됩니다.

소프트맥스 함수(Softmax function)

소프트맥스 함수(Softmax function)는 로지스틱 함수의 다차원 일반화입니다.

다항 로지스틱 회귀에서 쓰입니다!

neural network에서는 확률분포를 얻기 위한 마지막 활성함수로 많이 사용됩니다.

이름과 달리 최댓값(max) 함수를 매끄럽거나 부드럽게 한 것이 아니라,

최댓값의 인수인 원핫(one-hot) 형태의 arg max 함수를 매끄럽게 해주는 역할을 합니다.

그 계산 방법은 입력값을 자연로그의 밑을 밑으로 한 지수 함수를 취한 뒤 그 지수함수의 합으로 나눠주는 방식입니다.

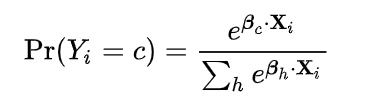
다시 쉽게 정리를 해보자면,

소프트맥스 함수는 선택해야 하는 선택지가 총 k개 있을 때, k차원의 벡터를 입력받아 각 클래스에 대한 확률을 추정하는 함수입니다.

softmax는 다항 로지스틱 회귀 분석중 하나이고, linear classification을 여러번 결합한 결과입니다.

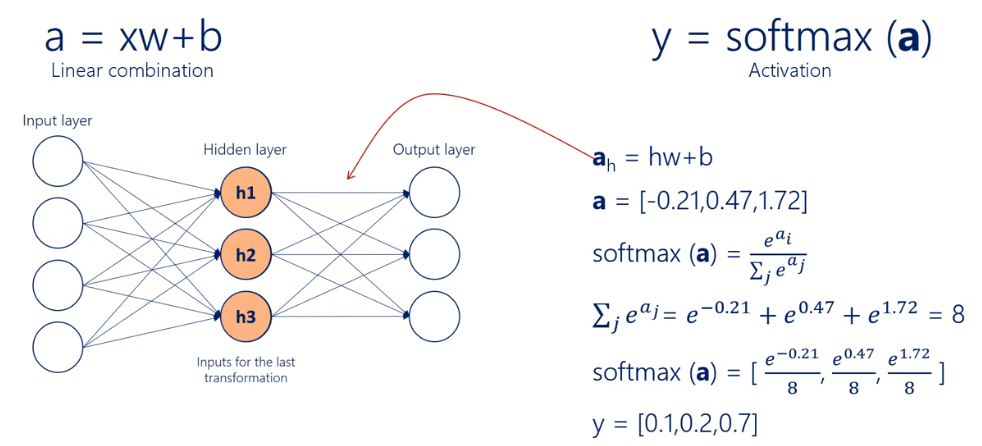
*이미지 출처:https://jjeongil.tistory.com/977

위 그림을 참고 부탁드립니다.

선형 회귀랑 다른 점?

여기서 궁금한 점이 하나 생겼는데요. 로지스틱 회귀를 너무 머리 싸매고 공부하다 보니 선형 회귀와 다른 점이 궁금해졌습니다.

로지스틱 회귀의 기본적인 접근은 이미 개발되어 있는 선형 회귀의 방식을 사용하는 것이었습니다.

독립 변수의 선형 결합과 회귀 계수에 관한 선형 예측 함수에서 비롯되었습니다.

하지만, 로지스틱 회귀의 모델은 종속 변수와 독립 변수 사이의 관계에 있어서 선형 모델과 차이점을 지니고 있습니다.

1. 이항 분류 데이터에 적용했을 때, 종속 변수 y의 결과가 범위 [0,1]로 제한됩니다.

2. 종속 변수가 이진적이기 때문에 조건부 확률(P(y│x))의 분포가 정규분포 대신 이항 분포를 따릅니다.

그래서 아까 로짓 변환을 시켜주었죠🙂

따라서 대상이 되는 데이터의 종속 변수 $y$의 결과는 0과 1, 두 개의 경우만 존재하는 데 반해

단순 선형 회귀를 적용하면 범위 [0,1]를 벗어나는 결과가 나오기 때문에 오히려 예측의 정확도만 떨어뜨리게 됩니다.

이를 해결하기 위해 로지스틱 회귀는 연속이고 증가함수이며 [0,1]에서 값을 갖는 연결 함수 g(x) 형태로 변형 시켜주었습니다.

최종 정리

지금까지 로지스틱 회귀에 대해 공부하였습니다.

• 로지스틱 회귀란? 선형 방정식을 사용한 분류 알고리즘. 선형 회귀와 달리 시그모이드, 소프트맥스 함수를 사용하여 클래스 확률을 출력함
• 다중 분류란? 타깃 클래스가 2개 이상인 분류 문제. 로지스틱 회귀는 다중 분류를 위해 소프트맥스 함수를 사용하여 클래스를 예측함
• 시그모이드 함수란? 로지스틱 함수라고도 함. 출력을 0과 1 사이의 값으로 압축하며 이진 분류를 위해 사용됨
• 소프트 맥스 함수란? 다중 분류에서 여러 선형 방정식의 출력 결과를 정규화하여 합이 1이 되도록 만듦

고생 많으셨습니다.👏👏👏